Estimating the Quality of the Most Popular Machine Learning Algorithms for Landslide Susceptibility Mapping in 2018 Mw 7.5 Palu Earthquake
Abstract
:1. Introduction
2. Geological Setting and Landslide Inventory of Palu Earthquake
2.1. Geological Setting
2.2. Landslide Inventory of the Palu Earthquake
3. Data and Methods
3.1. Data Sources
3.2. Method
4. Results
5. Discussion
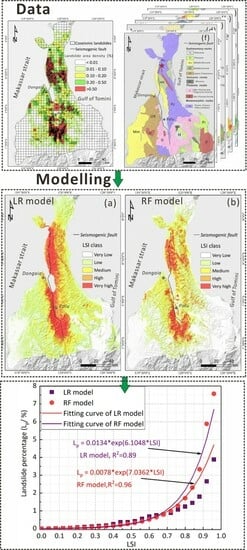
5.1. Converting LSI to Landslide Percentage (Lp)
5.2. Relative Importance of the Influencing Factors
5.3. Comparisons of the RF Model with LR Model
6. Conclusions
- (1)
- Based on the LSM predicted by two models and actual landslides, the landslide abundance area roughly matches the area of high LSI, with areas with LSI mainly concentrated along both sides of the seismogenic fault. The areas with high LSI mainly include the southern part of the epicenter and the areas on both sides of the Palu basin, which are also the landslide abundance areas.
- (2)
- Compared to the LR model, the std of the RF model is smaller, with a max std of 0.13. The std based on the RF model is lower than that of the LR model, indicating that the evaluation results based on the RF model are less affected by the changes in training samples, while the predicted result of the LR model has a relatively large variation in LSI with the changes in training samples.
- (3)
- The assessment results based on the RF model are less affected by the changes in the training samples, while the predicted result of the LR model has a relatively large variation in LSI with the changes in the training samples. Both models demonstrate satisfactory performance; the RF model exhibits higher predictive capability compared to the LR model. The RF model, with a predicted rate of 0.94, is significantly higher than the rate of 0.86 for the LR model. Overall, the LR and RF models are useful tools for LSM of seismic events.
- (4)
- We calculate the probability of landslide occurrence and average LSI for each interval using 0.05 width bins, and then fit the relationship between LSI and landslide percentage (Lp). The results indicate that there is a clear exponential relationship between the LSI and the landslide percentage (Lp) of for the LR model and for the RF model. This equation can be used to correct the LSI to represent the landslide percentage (Lp) when the 1:1 ratio of landsliding/non-landsliding is used for modelling of the Palu area.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fan, X.; Scaringi, G.; Korup, O.; West, A.J.; van Westen, C.J.; Tanyas, H.; Hovius, N.; Hales, T.C.; Jibson, R.W.; Allstadt, K.E.; et al. Earthquake-induced chains of geologic hazards: Patterns, mechanisms, and impacts. Rev. Geophys. 2019, 57, 421–503. [Google Scholar] [CrossRef]
- Gorum, T.; van Westen, C.J.; Korup, O.; van der Meijde, M.; Fan, X.; van der Meer, F.D. Complex rupture mechanism and topography control symmetry of mass-wasting pattern, 2010 Haiti earthquake. Geomorphology 2013, 184, 127–138. [Google Scholar] [CrossRef]
- Havenith, H.B.; Guerrier, K.; Schlögel, R.; Braun, A.; Ulysse, S.; Mreyen, A.S.; Victor, K.H.; Saint-Fleur, N.; Cauchie, L.; Boisson, D.; et al. Earthquake-induced landslides in Haiti: Analysis of seismotectonic and possible climatic influences. Nat. Hazards Earth Syst. Sci. 2022, 22, 3361–3384. [Google Scholar] [CrossRef]
- Shao, X.; Ma, S.; Xu, C. Distribution and characteristics of shallow landslides triggered by the 2018 Mw 7.5 Palu earthquake, Indonesia. Landslides 2023, 20, 157–175. [Google Scholar] [CrossRef]
- Shao, X.; Ma, S.; Xu, C.; Zhang, P.; Wen, B.; Tian, Y.; Zhou, Q.; Cui, Y. Planet Image-Based Inventorying and Machine Learning-Based Susceptibility Mapping for the Landslides Triggered by the 2018 Mw6.6 Tomakomai, Japan Earthquake. Remote Sens. 2019, 11, 978. [Google Scholar] [CrossRef]
- Zhao, B.; Hu, K.; Yang, Z.; Liu, Q.; Zou, Q.; Chen, H.; Zhang, W.; Zhu, L.; Su, L.-J. Geomorphic and tectonic controls of landslides induced by the 2022 Luding earthquake. J. Mt. Sci. 2022, 19, 3323–3345. [Google Scholar] [CrossRef]
- Shao, X.; Xu, C.; Ma, S. Preliminary analysis of coseismic landslides induced by the 1 June 2022 Ms 6.1 Lushan Earthquake, China. Sustainability 2022, 14, 16554. [Google Scholar] [CrossRef]
- Gorum, T.; Korup, O.; van Westen, C.J.; van der Meijde, M.; Xu, C.; van der Meer, F.D. Why so few? Landslides triggered by the 2002 Denali earthquake, Alaska. Quat. Sci. Rev. 2014, 95, 80–94. [Google Scholar] [CrossRef]
- Shao, X.; Xu, C.; Ma, S.; Shyu, J.; Zhou, Q. Calculation of landslide occurrence probability in Taiwan region under different ground motion conditions. J. Mt. Sci. 2021, 18, 1003–1012. [Google Scholar] [CrossRef]
- Robinson, T.R.; Rosser, N.J.; Densmore, A.L.; Williams, J.G.; Kincey, M.E.; Benjamin, J.; Bell, H.J.A. Rapid post-earthquake modelling of coseismic landslide intensity and distribution for emergency response decision support. Nat. Hazards Earth Syst. Sci. 2017, 17, 1521–1540. [Google Scholar] [CrossRef]
- Lombardo, L.; Bakka, H.; Tanyas, H.; Westen, C.; Mai, P.M.; Huser, R. Geostatistical Modeling to Capture Seismic-Shaking Patterns From Earthquake-Induced Landslides. J. Geophys. Res. Earth Surf. 2019, 124, 1958–1980. [Google Scholar] [CrossRef]
- Chalkias, C.; Ferentinou, M.; Polykretis, C. GIS-Based Landslide Susceptibility Mapping on the Peloponnese Peninsula, Greece. Geosciences 2014, 4, 176–190. [Google Scholar] [CrossRef]
- Parker, R.N.; Densmore, A.L.; Rosser, N.J.; de Michele, M.; Li, Y.; Huang, R.; Whadcoat, S.; Petley, D.N. Mass wasting triggered by the 2008 Wenchuan earthquake is greater than orogenic growth. Nat. Geosci. 2011, 4, 449–452. [Google Scholar] [CrossRef]
- Xiong, J.; Chen, M.; Tang, C. Long-term changes in the landslide sediment supply capacity for debris flow occurrence in Wenchuan County, China. Catena 2021, 203, 105340. [Google Scholar] [CrossRef]
- Tian, Y.; Owen, L.A.; Xu, C.; Ma, S.; Li, K.; Xu, X.; Figueiredo, P.M.; Kang, W.; Guo, P.; Wang, S.; et al. Landslide development within 3 years after the 2015 Mw 7.8 Gorkha earthquake, Nepal. Landslides 2020, 17, 1251–1267. [Google Scholar] [CrossRef]
- Ma, S.; Xu, C.; Shao, X. Spatial prediction strategy for landslides triggered by large earthquakes oriented to emergency response, mid-term resettlement and later reconstruction. Int. J. Disaster Risk Reduct. 2020, 43, 101362. [Google Scholar] [CrossRef]
- Massey, C.; Townsend, D.; Rathje, E.; Allstadt, K.E.; Lukovic, B.; Kaneko, Y.; Bradley, B.; Wartman, J.; Jibson, R.W.; Petley, D.N.; et al. Landslides Triggered by the 14 November 2016 Mw 7.8 Kaikōura Earthquake, New Zealand. Bull. Seismol. Soc. Am. 2018, 108, 1630–1648. [Google Scholar] [CrossRef]
- Chen, Z.; Song, D. Modeling landslide susceptibility based on convolutional neural network coupling with metaheuristic optimization algorithms. Int. J. Digit. Earth 2023, 16, 3384–3416. [Google Scholar] [CrossRef]
- Huang, F.; Yan, J.; Fan, X.; Yao, C.; Huang, J.; Chen, W.; Hong, H. Uncertainty pattern in landslide susceptibility prediction modelling: Effects of different landslide boundaries and spatial shape expressions. Geosci. Front. 2022, 13, 101317. [Google Scholar] [CrossRef]
- Chen, X.L.; Liu, C.G.; Yu, L.; Lin, C.X. Critical acceleration as a criterion in seismic landslide susceptibility assessment. Geomorphology 2014, 217, 15–22. [Google Scholar] [CrossRef]
- Huang, D.; Wang, G.; Du, C.; Jin, F.; Feng, K.; Chen, Z. An integrated SEM-Newmark model for physics-based regional coseismic landslide assessment. Soil Dyn. Earthq. Eng. 2020, 132, 106066. [Google Scholar] [CrossRef]
- Newmark, N.M. Effects of earthquakes on dams and embankments. Géotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef]
- Wang, T.; Wu, S.R.; Shi, J.S.; Xin, P.; Wu, L.Z. Assessment of the effects of historical strong earthquakes on large-scale landslide groupings in the Wei River midstream. Eng. Geol. 2018, 235, 11–19. [Google Scholar] [CrossRef]
- Jibson, R.W. Methods for assessing the stability of slopes during earthquakes—A retrospective. Eng. Geol. 2011, 122, 43–50. [Google Scholar] [CrossRef]
- Jibson, R.W.; Harp, E.L.; Michael, J.A. A method for producing digital probabilistic seismic landslide hazard maps: An example from the Los Angeles, California, area. Eng. Geol. 2000, 58, 271–289. [Google Scholar] [CrossRef]
- Godt, J.W.; Sener, B.; Verdin, K.L.; Wald, D.J.; Earle, P.S.; Harp, E.L.; Jibson, R.W. Rapid assessment of earthquake-induced landsliding. In Proceedings of the First World Landslide Forum, Tokyo, Japan, 18–21 November 2008. [Google Scholar]
- Ma, S.Y.; Xu, C. Assessment of co-seismic landslide hazard using the Newmark model and statistical analyses: A case study of the 2013 Lushan, China, Mw6.6 earthquake. Nat. Hazards 2019, 96, 389–412. [Google Scholar] [CrossRef]
- Chen, X.; Liu, C.; Wang, M. A method for quick assessment of earthquake-triggered landslide hazards: A case study of the Mw6.1 2014 Ludian, China earthquake. Bull. Eng. Geol. Environ. 2019, 78, 2449–2458. [Google Scholar] [CrossRef]
- Gallen, S.F.; Clark, M.K.; Godt, J.W.; Roback, K.; Niemi, N.A. Application and evaluation of a rapid response earthquake-triggered landslide model to the 25 April 2015 Mw 7.8 Gorkha earthquake, Nepal. Tectonophysics 2017, 714–715, 173–187. [Google Scholar] [CrossRef]
- Yue, X.; Wu, S.; Yin, Y.; Gao, J.; Zheng, J. Risk Identification of Seismic Landslides by Joint Newmark and RockFall Analyst Models: A Case Study of Roads Affected by the Jiuzhaigou Earthquake. Int. J. Disaster Risk Sci. 2018, 9, 392–406. [Google Scholar] [CrossRef]
- Du, G.; Zhang, Y.; Zou, L.; Yang, Z.; Yuan, Y.; Ren, S. Co-seismic landslide hazard assessment of the 2017 Ms 6.9 Milin earthquake, Tibet, China, combining the logistic regression–information value and Newmark displacement models. Bull. Eng. Geol. Environ. 2022, 81, 446. [Google Scholar] [CrossRef]
- Dreyfus, D.K.; Rathje, E.M.; Jibson, R.W. The influence of different simplified sliding-block models and input parameters on regional predictions of seismic landslides triggered by the Northridge earthquake. Eng. Geol. 2013, 163, 41–54. [Google Scholar] [CrossRef]
- Guzzetti, F.; Carrara, A.; Cardinali, M.; Paola, R. Landslide hazard evaluation: A review of current techniques and their application in a multi-scale study, Central Italy. Geomorphology 1999, 31, 181–216. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Xu, C.; Tien Bui, D. Spatial prediction of landslide hazard at the Yihuang area (China) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. An assessment of multivariate and bivariate approaches in landslide susceptibility mapping: A case study of Duzkoy district. Nat. Hazards 2015, 76, 471–496. [Google Scholar] [CrossRef]
- Xu, C.; Xu, X.; Dai, F.; Saraf, A.K. Comparison of different models for susceptibility mapping of earthquake triggered landslides related with the 2008 Wenchuan earthquake in China. Comput. Geosci. 2012, 46, 317–329. [Google Scholar] [CrossRef]
- Arabameri, A.; Chandra Pal, S.; Rezaie, F.; Chakrabortty, R.; Saha, A.; Blaschke, T.; Di Napoli, M.; Ghorbanzadeh, O.; Thi Ngo, P.T. Decision tree based ensemble machine learning approaches for landslide susceptibility mapping. Geocarto Int. 2021, 37, 4594–4627. [Google Scholar] [CrossRef]
- He, Q.; Wang, M.; Liu, K. Rapidly assessing earthquake-induced landslide susceptibility on a global scale using random forest. Geomorphology 2021, 391, 107889. [Google Scholar] [CrossRef]
- Sahin, E.K. Implementation of free and open-source semi-automatic feature engineering tool in landslide susceptibility mapping using the machine-learning algorithms RF, SVM, and XGBoost. Stoch. Environ. Res. Risk Assess. 2023, 37, 1067–1092. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Hong, H. Comparison of convolutional neural networks for landslide susceptibility mapping in Yanshan County, China. Sci. Total Environ. 2019, 666, 975–993. [Google Scholar] [CrossRef] [PubMed]
- Pourghasemi, H.R.; Rahmati, O. Prediction of the landslide susceptibility: Which algorithm, which precision? Catena 2018, 162, 177–192. [Google Scholar] [CrossRef]
- Hall, R. Cenozoic geological and plate tectonic evolution of SE Asia and the SW Pacific: Computer-based reconstructions, model and animations. J. Asian Earth Sci. 2002, 20, 353–431. [Google Scholar] [CrossRef]
- Puntodewo, S.S.O.; McCaffrey, R.; Calais, E.; Bock, Y.; Rais, J.; Subarya, C.; Poewariardi, R.; Stevens, C.; Genrich, J.; Fauzi; et al. GPS measurements of crustal deformation within the Pacific-Australia plate boundary zone in Irian Jaya, Indonesia. Tectonophysics 1994, 237, 141–153. [Google Scholar] [CrossRef]
- Wallace, L.M.; McCaffrey, R.; Beavan, J.; Ellis, S. Rapid microplate rotations and backarc rifting at the transition between collision and subduction. Geology 2005, 33, 857–860. [Google Scholar] [CrossRef]
- Socquet, A.; Hollingsworth, J.; Pathier, E.; Bouchon, M. Evidence of supershear during the 2018 magnitude 7.5 Palu earthquake from space geodesy. Nat. Geosci. 2019, 12, 192–199. [Google Scholar] [CrossRef]
- Watkinson, I.; Hall, R. Fault systems of the eastern Indonesian triple junction: Evaluation of Quaternary activity and implications for seismic hazards. Geol. Soc. Lond. Spec. Publ. 2017, 441, 71–120. [Google Scholar] [CrossRef]
- Watkinson, I. Ductile flow in the metamorphic rocks of central Sulawesi. Geol. Soc. Lond. Spec. Publ. 2011, 355, 157–176. [Google Scholar] [CrossRef]
- Natawidjaja, D.H.; Daryono, M.R.; Prasetya, G.; Liu, P.L.; Hananto, N.D.; Kongko, W.; Triyoso, W.; Puji, A.R.; Meilano, I.; Gunawan, E.; et al. The 2018 Mw7.5 Palu ‘supershear’ earthquake ruptures geological fault’s multisegment separated by large bends: Results from integrating field measurements, LiDAR, swath bathymetry and seismic-reflection data. Geophys. J. Int. 2020, 224, 985–1002. [Google Scholar] [CrossRef]
- Zhao, B. Landslides triggered by the 2018 Mw 7.5 Palu supershear earthquake in Indonesia. Eng. Geol. 2021, 294, 106406. [Google Scholar] [CrossRef]
- Nowicki Jessee, M.A.; Hamburger, M.W.; Allstadt, K.; Wald, D.J.; Robeson, S.M.; Tanyas, H.; Hearne, M.; Thompson, E.M. A global empirical model for near-real-time assessment of seismically induced landslides. J. Geophys. Res. Earth Surf. 2019, 123, 1835–1859. [Google Scholar] [CrossRef]
- Indonesian Geospatial Information Agency. DEMNAS—Seamless Digital Elevation Model (DEM) Dan Batimetri Nasional. 2019. Available online: http://tides.big.go.id/DEMNAS/ (accessed on 18 January 2019).
- van Leeuwen, T.M. Stratigraphy and tectonic setting of the Cretaceous and Paleogene volcanic-sedimentary successions in northwest Sulawesi, Indonesia: Implications for the Cenozoic evolution of Western and Northern Sulawesi. J. Asian Earth Sci. 2005, 25, 481–511. [Google Scholar] [CrossRef]
- USGS. United States Geological Survey. 2018. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us1000h3p4/executive (accessed on 18 January 2019).
- Dai, F.C.; Lee, C.F. Landslide characteristics and slope instability modeling using GIS, Lantau Island, Hong Kong. Geomorphology 2002, 42, 213–228. [Google Scholar] [CrossRef]
- Budimir, M.E.A.; Atkinson, P.M.; Lewis, H.G. A systematic review of landslide probability mapping using logistic regression. Landslides 2015, 12, 419–436. [Google Scholar] [CrossRef]
- Tanyas, H.; Rossi, M.; Alvioli, M.; van Westen, C.J.; Marchesini, I. A global slope unit-based method for the near real-time prediction of earthquake-induced landslides. Geomorphology 2019, 327, 126–146. [Google Scholar] [CrossRef]
- Shao, X.; Ma, S.; Xu, C.; Zhou, Q. Effects of sampling intensity and non-slide/slide sample ratio on the occurrence probability of coseismic landslides. Geomorphology 2020, 363, 107222. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Bureau, A.; Dupuis, J.; Hayward, B.; Falls, K.; Van Eerdewegh, P. Mapping complex traits using Random Forests. BMC Genet. 2003, 4, S64. [Google Scholar] [CrossRef]
- Stumpf, A.; Kerle, N. Object-oriented mapping of landslides using Random Forests. Remote Sens. Environ. 2011, 115, 2564–2577. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Cantarino, I.; Carrion, M.A.; Goerlich, F.; Martinez Ibañez, V. A ROC analysis-based classification method for landslide susceptibility maps. Landslides 2018, 16, 265–282. [Google Scholar] [CrossRef]
- Brenning, A. Spatial prediction models for landslide hazards: Review, comparison and evaluation. Nat. Hazards Earth Syst. Sci. 2005, 5, 853–862. [Google Scholar] [CrossRef]
- Hong, H.; Miao, Y.; Liu, J.; Zhu, A.X. Exploring the effects of the design and quantity of absence data on the performance of random forest-based landslide susceptibility mapping. Catena 2019, 176, 45–64. [Google Scholar] [CrossRef]
- Lee, C.T. Statistical seismic landslide hazard analysis: An example from Taiwan. Eng. Geol. 2014, 182, 201–212. [Google Scholar] [CrossRef]
- Shao, X.; Xu, C. Earthquake-induced landslides susceptibility assessment: A review of the state-of-the-art. Nat. Hazards Res. 2022, 2, 172–182. [Google Scholar] [CrossRef]















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Shao, X.; Xu, C. Estimating the Quality of the Most Popular Machine Learning Algorithms for Landslide Susceptibility Mapping in 2018 Mw 7.5 Palu Earthquake. Remote Sens. 2023, 15, 4733. https://doi.org/10.3390/rs15194733
Ma S, Shao X, Xu C. Estimating the Quality of the Most Popular Machine Learning Algorithms for Landslide Susceptibility Mapping in 2018 Mw 7.5 Palu Earthquake. Remote Sensing. 2023; 15(19):4733. https://doi.org/10.3390/rs15194733
Chicago/Turabian StyleMa, Siyuan, Xiaoyi Shao, and Chong Xu. 2023. "Estimating the Quality of the Most Popular Machine Learning Algorithms for Landslide Susceptibility Mapping in 2018 Mw 7.5 Palu Earthquake" Remote Sensing 15, no. 19: 4733. https://doi.org/10.3390/rs15194733
APA StyleMa, S., Shao, X., & Xu, C. (2023). Estimating the Quality of the Most Popular Machine Learning Algorithms for Landslide Susceptibility Mapping in 2018 Mw 7.5 Palu Earthquake. Remote Sensing, 15(19), 4733. https://doi.org/10.3390/rs15194733