First-Break Picking of Large-Offset Seismic Data Based on CNNs with Weighted Data
Abstract
:1. Introduction
2. Theory and Methods
2.1. Basic Principles of CNNs
2.1.1. Convolutional Layer
2.1.2. Pooling Layer
2.1.3. Fully Connected Layer
2.2. Processing Flow
2.2.1. Sample Set Production
- (1)
- Linear correction time window: When training the network, it is necessary to apply the seismic records and the corresponding first arrivals of the common shot point data to the trainer as inputs and labels, because the first arrivals only offer information such as direct waves and subsequently covered refraction waves, etc. If the full-time seismic data features are extracted for training, there will be a large amount of redundant information, and this will prolong the training time. Therefore, a linear correction time window was designed in this study to extract the seismic records close to the time of the first arrivals as the training input data. At the same time, the linear correction travel–time difference was determined according to the maximum left and right offset distances intercepted by the time window, the endpoint moments of the window function, and the difference in the seismic wave arrival time of the minimum offset so as to compress the seismic signals in the time field into a rectangular box, which can better utilize the spatial correlation of the first arrivals and reduce the input volume in order to improve the training efficiency. Figure 2 shows a comparison before and after the linear correction of the 130th and 190th shots. Although the time window does not flatten the intercepted first arrivals to a sufficient extent, it is very easy to handle, in the case of either single or multiple shots, by simply obtaining the first, last, and shot point first arrivals of each shot and then using these three values for the interception of the time window. In this paper, the time window is defined by time-shifting the timeline by in the upper and lower directions, respectively, and the mathematical expressions for the timeline and the linear correction time are calculated as:
- (2)
- Increasing the weight of the far-offset data among the training data: Since seismic data have a good signal-to-noise ratio at the near offsets and a low signal-to-noise ratio at the far offsets, the effective signal is suppressed by noise, making it difficult to identify the first arrivals using traditional methods or industrial software. In order to improve the first-break picking accuracy of the network for the far offsets, in this paper, we propose a far-offset-data-weighting strategy, which sets all the single-shot records after the linear time window interception within 10 km of the shot location as the near-offset dataset and the rest as the far-offset dataset. In order to increase the weight of the far-offset data in the training dataset, the near-offset dataset of half of the single-shot records is randomly dropped from the training dataset, and the ratio of the near-offset dataset to the far-offset dataset is set as 1:2 to obtain the final training data. Weighting enables CNNs to learn more feature patterns of far offsets with a poor signal-to-noise ratio and the corresponding first arrivals, thus improving the prediction accuracy of the CNNs for far-offset first arrivals.
- (3)
- Seismic data trace editing: The detector is affected by environmental factors, the machine’s specific factors, and other factors during the work, and some invalid traces, bad traces, polarity reversal traces, etc., will appear in the data. In order to render the network unaffected by these traces, a certain number of invalid traces, abnormal data traces, polar traces, etc., are artificially added to the training data to improve the generalizability of the network.
- (4)
- Processing of the labels: In the process of generating labeled images, all the data points before the first arrivals are labeled as −1, and those after the first arrivals are labeled as 1. Figure 3 shows the results of the label data processing for the 190th shot. From the results, we can observe that the obtained labeled data appear to be white in the upper part and black in the lower part, and their size is consistent with the grayscale figure. The reason for this treatment is that [–1, 1] is consistent with the characteristics of seismic data, and this treatment is closer to a process of classifying the training data than that of directly outputting the first arrival time, which is more conducive to the extraction of first arrival features by the network model.
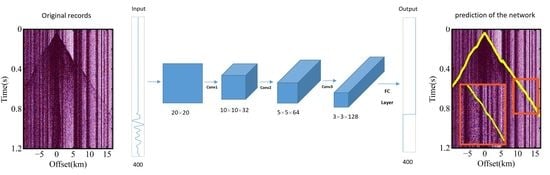
2.2.2. Network Construction
3. Results
Tomography Images Comparison
Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Oliver, J.; Cook, F.; Brown, L. COCORP and the continental crust. J. Geophys. Res. Solid Earth 1983, 88, 3329–3347. [Google Scholar] [CrossRef]
- Brown, L.; Wille, D.; Zheng, L.; DeVoogd, B.; Mayer, J.; Hearn, T.; Sanford, W.; Caruso, C.; Zhu, T.F.; Nelson, D.; et al. COCORP: New perspectives on the deep crust. Geophys. J. Int. 1987, 89, 47–54. [Google Scholar] [CrossRef] [Green Version]
- Chadwick, R.A.; Pharaoh, T.C. The seismic reflection Moho beneath the United Kingdom and adjacent areas. Tectonophysics 1998, 299, 255–279. [Google Scholar] [CrossRef]
- Clowes, R.; Cook, F.; Hajnal, Z.; Hall, J.; Lewry, J.; Lucas, S.; Wardle, R. Canada’s LITHOPROBE Project (Collaborative, multidisciplinary geoscience research leads to new understanding of continental evolution). Epis. J. Int. Geosci. 1999, 22, 3–20. [Google Scholar] [CrossRef] [Green Version]
- Cook, F.A. Fine structure of the continental reflection Moho. Geol. Soc. Am. Bull. 2002, 114, 64–79. [Google Scholar] [CrossRef]
- Zhao, W.; Kumar, P.; Mechie, J.; Kind, R.; Meissner, R.; Wu, Z.; Shi, D.; Su, H.; Xue, G.; Karplus, M.; et al. Tibetan plate overriding the Asian plate in central and northern Tibet. Nat. Geosci. 2011, 4, 870–873. [Google Scholar] [CrossRef]
- Gao, R.; Chen, C.; Lu, Z.; Brown, L.; Xiong, X.; Li, W.; Deng, G. New constraints on crustal structure and Moho topography in Central Tibet revealed by SinoProbe deep seismic reflection profiling. Tectonophysics 2013, 606, 160–170. [Google Scholar] [CrossRef] [Green Version]
- Lu, Z.; Gao, R.; Li, Y.; Xue, A.; Li, Q.; Wang, H.; Kuang, C.; Xiong, X. The upper crustal structure of the Qiangtang Basin revealed by seismic reflection data. Tectonophysics 2013, 606, 171–177. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Gao, R.; Han, L.; Lu, Z. Refraction waves full waveform inversion of deep reflection seismic profiles in the central part of Lhasa Terrane. Tectonophysics 2021, 803, 228761. [Google Scholar] [CrossRef]
- Stevenson, P.R. Microearthquakes at Flathead Lake, Montana: A study using automatic earthquake processing. Bull. Seismol. Soc. Am. 1976, 66, 61–80. [Google Scholar] [CrossRef]
- Allen, R.V. Automatic earthquake recognition and timing from single traces. Bull. Seismol. Soc. Am. 1978, 68, 1521–1532. [Google Scholar] [CrossRef]
- Baranov, S.V. Application of the wavelet transform to automatic seismic signal detection. Izv. Phys. Solid Earth 2007, 43, 177–188. [Google Scholar] [CrossRef]
- Ross, Z.E.; Ben-Zion, Y. An earthquake detection algorithm with pseudo-probabilities of multiple indicators. Geophys. J. Int. 2014, 197, 458–463. [Google Scholar] [CrossRef] [Green Version]
- Akram, J.; Peter, D.; Eaton, D. A k-mean characteristic function for optimizing short-and long-term-average-ratio-based detection of microseismic events. Geophysics 2019, 84, KS143–KS153. [Google Scholar] [CrossRef] [Green Version]
- Coppens, F. First arrival picking on common-offset trace collections for automatic estimation of static corrections. Geophys. Prospect. 1985, 33, 1212–1231. [Google Scholar] [CrossRef]
- Boschetti, F.; Dentith, M.D.; List, R.D. A fractal-based algorithm for detecting first arrivals on seismic traces. Geophysics 1996, 61, 1095–1102. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Mężyk, M.; Malinowski, M. Multi-pattern algorithm for first-break picking employing open-source machine learning libraries. J. Appl. Geophys. 2019, 170, 103848. [Google Scholar] [CrossRef]
- McCormack, M.D.; Zaucha, D.E.; Dushek, D.W. First-break refraction event picking and seismic data trace editing using neural networks. Geophysics 1993, 58, 67–78. [Google Scholar] [CrossRef]
- Maity, D.; Aminzadeh, F.; Karrenbach, M. Novel hybrid artificial neural network based autopicking workflow for passive seismic data. Geophys. Prospect. 2014, 62, 834–847. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Horton, S.P.; Langston, C.A.; Samei, B. Seismic features and automatic discrimination of deep and shallow induced-microearthquakes using neural network and logistic regression. Geophys. J. Int. 2016, 207, 29–46. [Google Scholar] [CrossRef] [Green Version]
- Yuan, S.; Liu, J.; Wang, S.; Wang, T.; Shi, P. Seismic waveform classification and first-break picking using convolution neural networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 272–276. [Google Scholar] [CrossRef] [Green Version]
- Duan, X.; Zhang, J. Multitrace first-break picking using an integrated seismic and machine learning methodPicking based on machine learning. Geophysics 2020, 85, WA269–WA277. [Google Scholar] [CrossRef]
- Murat, M.E.; Rudman, A.J. Automated first arrival picking: A neural network approach. Geophys. Prospect. 1992, 40, 587–604. [Google Scholar] [CrossRef]
- Qu, S.; Guan, Z.; Verschuur, E.; Chen, Y. Expression of Concern: Automatic high-resolution microseismic event detection via supervised machine learning. Geophys. J. Int. 2020, 221, 2056. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Zhang, B.; Li, F.; Liu, N. Semiautomatic first-arrival picking of microseismic events by using the pixel-wise convolutional image segmentation method. Geophysics 2019, 84, V143–V155. [Google Scholar] [CrossRef]








| Layer Name | CNN-3 | CNN-4 |
|---|---|---|
| Input | [400 × 1 × 1] reshape Output: [20 × 20 × 1] | |
| Conv1 + Pool1 | [3 × 3, 32] max pool, stride 2 Output: [10 × 10 × 32] | |
| Conv2 + Pool2 | [3 × 3, 64] max pool, stride 2 Output: [5 × 5 × 64] | |
| Conv3 + Pool3 | [3 × 3, 128] max pool, stride 2 Output: [3 × 3 × 128] | |
| Conv4 + Pool4 | - | [3 × 3, 256] max pool, stride 2 Output: [2 × 2 × 256] |
| Ful1 | [1024 × 1 × 1] | |
| Ful2 | [512 × 1 × 1] | |
| Ful3 | [480 × 1 × 1] | |
| output | [400 × 1 × 1] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Y.; Han, L.; Zhang, P.; Lu, Z.; Shang, X. First-Break Picking of Large-Offset Seismic Data Based on CNNs with Weighted Data. Remote Sens. 2023, 15, 356. https://doi.org/10.3390/rs15020356
Yin Y, Han L, Zhang P, Lu Z, Shang X. First-Break Picking of Large-Offset Seismic Data Based on CNNs with Weighted Data. Remote Sensing. 2023; 15(2):356. https://doi.org/10.3390/rs15020356
Chicago/Turabian StyleYin, Yuchen, Liguo Han, Pan Zhang, Zhanwu Lu, and Xujia Shang. 2023. "First-Break Picking of Large-Offset Seismic Data Based on CNNs with Weighted Data" Remote Sensing 15, no. 2: 356. https://doi.org/10.3390/rs15020356
APA StyleYin, Y., Han, L., Zhang, P., Lu, Z., & Shang, X. (2023). First-Break Picking of Large-Offset Seismic Data Based on CNNs with Weighted Data. Remote Sensing, 15(2), 356. https://doi.org/10.3390/rs15020356