First Demonstration of Space-Borne Polarization Coherence Tomography for Characterizing Hyrcanian Forest Structural Diversity
Abstract
:1. Introduction
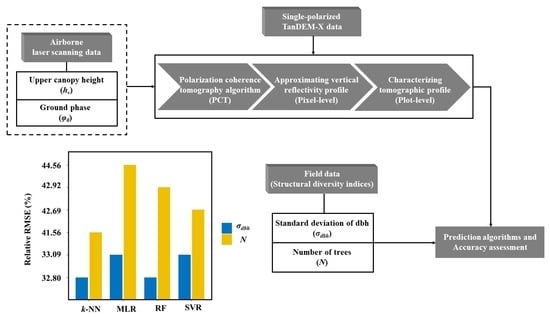
2. Materials and Methods
2.1. Site Description
2.2. Field Data and Structural Diversity Indices
2.3. TanDEM-X Data
2.4. Airborne Laser Scanning Data
2.4.1. Forest Height and Ground Phase Estimation
2.5. Polarization Coherence Tomography (PCT)
Characterizing Tomographic Profiles
2.6. Prediction Algorithms
2.7. Accuracy Assessment
3. Results
3.1. Correlation Analysis
3.2. Model Developments for Prediction of
3.3. Model Developments for Prediction of
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Spies, T.A. Forest Structure: A Key to the Ecosystem. Northwest Sci. 1998, 72, 34–39. [Google Scholar]
- Del Río, M.; Pretzsch, H.; Alberdi, I.; Bielak, K.; Bravo, F.; Brunner, A.; Condés, S.; Ducey, M.J.; Fonseca, T.; von Lüpke, N.; et al. Characterization of the Structure, Dynamics, and Productivity of Mixed-Species Stands: Review and Perspectives. Eur. J. For. Res. 2016, 135, 23–49. [Google Scholar] [CrossRef]
- Bergen, K.M.; Goetz, S.J.; Dubayah, R.O.; Henebry, G.M.; Hunsaker, C.T.; Imhoff, M.L.; Nelson, R.F.; Parker, G.G.; Radeloff, V.C. Remote Sensing of Vegetation 3-D Structure for Biodiversity and Habitat: Review and Implications for Lidar and Radar Spaceborne Missions. J. Geophys. Res. Biogeosciences 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Pakkala, T.; Hanski, I.; Tomppo, E. Spatial Ecology of the Three-Toed Woodpecker in Managed Forest Landscapes. Silva Fenn. 2002, 36, 279–288. [Google Scholar] [CrossRef] [Green Version]
- Bottalico, F.; Chirici, G.; Giannini, R.; Mele, S.; Mura, M.; Puxeddu, M.; McRoberts, R.E.; Valbuena, R.; Travaglini, D. Modeling Mediterranean Forest Structure Using Airborne Laser Scanning Data. Int. J. Appl. Earth Obs. Geoinf. 2017, 57, 145–153. [Google Scholar] [CrossRef]
- Chirici, G.; McRoberts, R.E.; Winter, S.; Bertini, R.; Bröändli, U.B.; Asensio, I.A.; Bastrup-Birk, A.; Rondeux, J.; Barsoum, N.; Marchetti, M. National Forest Inventory Contributions to Forest Biodiversity Monitoring. For. Sci. 2012, 58, 257–268. [Google Scholar] [CrossRef] [Green Version]
- McRoberts, R.E.; Winter, S.; Chirici, G.; la Point, E. Assessing Forest Naturalness. For. Sci. 2012, 58, 294–309. [Google Scholar] [CrossRef]
- Mura, M.; McRoberts, R.E.; Chirici, G.; Marchetti, M. Statistical Inference for Forest Structural Diversity Indices Using Airborne Laser Scanning Data and the K-Nearest Neighbors Technique. Remote Sens. Environ. 2016, 186, 678–686. [Google Scholar] [CrossRef]
- Neumann, M.; Starlinger, F. The Significance of Different Indices for Stand Structure and Diversity in Forests. For. Ecol. Manage. 2001, 145, 91–106. [Google Scholar] [CrossRef]
- Pommerening, A. Approaches to Quantifying Forest Structures. Forestry 2002, 75, 305–324. [Google Scholar] [CrossRef]
- Müller, J.; Vierling, K. Assessing Biodiversity by Airborne Laser Scanning; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- McRoberts, R.E.; Winter, S.; Chirici, G.; Hauk, E.; Pelz, D.R.; Moser, W.K.; Hatfield, M.A. Large-Scale Spatial Patterns of Forest Structural Diversity. Can. J. For. Res. 2008, 38, 429–438. [Google Scholar] [CrossRef]
- Staudhammer, C.L.; LeMay, V.M. Introduction and Evaluation of Possible Indices of Stand Structural Diversity. Can. J. For. Res. 2001, 31, 1105–1115. [Google Scholar] [CrossRef]
- Hall, F.G.; Bergen, K.; Blair, J.B.; Dubayah, R.; Houghton, R.; Hurtt, G.; Kellndorfer, J.; Lefsky, M.; Ranson, J.; Saatchi, S.; et al. Characterizing 3D Vegetation Structure from Space: Mission Requirements. Remote Sens. Environ. 2011, 115, 2753–2775. [Google Scholar] [CrossRef] [Green Version]
- Tian, X.; Su, Z.; Chen, E.; Li, Z.; van der Tol, C.; Guo, J.; He, Q. Estimation of Forest Above-Ground Biomass Using Multi-Parameter Remote Sensing Data over a Cold and Arid Area. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 160–168. [Google Scholar] [CrossRef]
- Tsui, O.W.; Coops, N.C.; Wulder, M.A.; Marshall, P.L. Integrating Airborne LiDAR and Space-Borne Radar via Multivariate Kriging to Estimate above-Ground Biomass. Remote Sens. Environ. 2013, 139, 340–352. [Google Scholar] [CrossRef]
- Poorazimy, M.; Shataee, S.; Attarchi, S.; Mohammadi, J. Estimation of Aboveground Biomass Using Alos-Palsar Data in Hyrcanian Forests (Case Study: ShastKalateh, Gorgan). For. Wood Prod. 2017, 70, 479–488. [Google Scholar]
- Poorazimy, M.; Shataee, S.; McRoberts, R.E.; Mohammadi, J. Integrating Airborne Laser Scanning Data, Space-Borne Radar Data and Digital Aerial Imagery to Estimate Aboveground Carbon Stock in Hyrcanian Forests, Iran. Remote Sens. Environ. 2020, 240, 111669. [Google Scholar] [CrossRef]
- Ronoud, G.; Fatehi, P.; Darvishsefat, A.A.; Tomppo, E.; Praks, J.; Schaepman, M.E. Multi-Sensor Aboveground Biomass Estimation in the Broadleaved Hyrcanian Forest of Iran. Can. J. Remote Sens. 2021, 47, 818–834. [Google Scholar] [CrossRef]
- Fornaro, G.; Lombardini, F.; Serafino, F. Three-Dimensional Multipass SAR Focusing: Experiments with Long-Term Spaceborne Data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 702–714. [Google Scholar] [CrossRef]
- Moreira, A.; Ponce, O.; Nannini, M.; Pardini, M.; Prats, P.; Reigber, A.; Papathanassiou, K.; Krieger, G. Multi-Baseline Spaceborne SAR Imaging. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1420–1423. [Google Scholar] [CrossRef]
- Lombardini, F.; Tebaldini, S. Multidimensional SAR Tomography: Methods and Applications. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Worth, TX, USA, 23–28 July 2017; pp. 2460–2463. [Google Scholar] [CrossRef]
- Aghababaei, H.; Ferraioli, G.; Ferro-Famil, L.; Huang, Y.; Mariotti D’Alessandro, M.; Pascazio, V.; Schirinzi, G.; Tebaldini, S. Forest SAR Tomography: Principles and Applications. IEEE Geosci. Remote Sens. Mag. 2020, 8, 30–45. [Google Scholar] [CrossRef]
- Lin, Q. Spaceborne Multibaseline SAR Tomography for Retrieving Forest Heights. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2017; p. 136. [Google Scholar]
- Huang, Y.; Ferro-Famil, L.; Neumann, M. Tropical Forest Structure Estimation Using Polarimetric SAR Tomography at P-Band. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 7593–7596. [Google Scholar] [CrossRef]
- Tebaldini, S.; Rocca, F. Multibaseline Polarimetric SAR Tomography of a Boreal Forest at P- and L-Bands. IEEE Trans. Geosci. Remote Sens. 2012, 50, 232–246. [Google Scholar] [CrossRef]
- Ho Tong Minh, D.; Le Toan, T.; Rocca, F.; Tebaldini, S.; D’Alessandro, M.M.; Villard, L. Relating P-Band Synthetic Aperture Radar Tomography to Tropical Forest Biomass. IEEE Trans. Geosci. Remote Sens. 2014, 52, 967–979. [Google Scholar] [CrossRef]
- Ferro-Famil, L.; Huang, Y.; El Hajj Chehade, B.; Reigber, A.; Tebaldini, S. 3-D Imaging Using Polarimetric Diversity, Processing Techniques and Applications. In Proceedings of the 2016 10th European Conference Antennas Propagation, EuCAP, Davos, Switzerland, 10–15 April 2016. [Google Scholar] [CrossRef]
- Cloude, S.R. Polarization Coherence Tomography. Radio Sci. 2006, 41, 1–27. [Google Scholar] [CrossRef]
- Praks, J.; Kuglet, F.; Hyyppa, J.; Papathanassiou, K.; Hallikainen, M. SAR Coherence Tomography for Boreal Forest with Aid of Laser Measurements. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; p. 2. [Google Scholar] [CrossRef] [Green Version]
- Huan Min, L.; Xiao Wen, L.; Er Xue, C.; Jian, C.; Chun Xiang, C. Analysis of Forest Backscattering Characteristics Based on Polarization Coherence Tomography. Sci. China Technol. Sci. 2010, 53, 166–175. [Google Scholar]
- Papathanassiou, K.; Pardini, M. Estimation of The Vertical Structure of Forests with\Rcoherence Tomography. In Proceedings of the ESA POLinSAR Workshop, Frascati, Italy, 24–28 January 2011. [Google Scholar]
- Renaudin, E.; Mercer, B. Forest Biomass Derivation from Single Pass Dual Baseline Polarisation Coherence Tomography. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 479–482. [Google Scholar] [CrossRef]
- Li, W.; Chen, E.; Li, Z.; Ke, Y.; Zhan, W. Forest Aboveground Biomass Estimation Using Polarization Coherence Tomography and PolSAR Segmentation. Int. J. Remote Sens. 2015, 36, 530–550. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, C.; Zhu, J.; Fu, H.; Xie, Q.; Shen, P. Forest Above-Ground Biomass Estimation Using Single-Baseline Polarization Coherence Tomography with P-Band PolInSAR Data. Forests 2018, 9, 163. [Google Scholar] [CrossRef] [Green Version]
- Ghasemi, N.; Tolpekin, V.A.; Stein, A. Estimating Tree Heights Using Multibaseline PolInSAR Data with Compensation for Temporal Decorrelation, Case Study: AfriSAR Campaign Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3464–3477. [Google Scholar] [CrossRef]
- Huanmin, L.U.O.; Erxue, C.; Zengyuan, L.I.; Chunxiang, C.A.O. Forest above Ground Biomass Estimation Methodology Based on Polarization Coherence Tomography. Yaogan Xuebao J. Remote Sens. 2011, 15, 1138–1155. [Google Scholar]
- Neumann, M.; Saatchi, S.S.; Ulander, L.M.H.; Fransson, J.E.S. Assessing Performance of L- and P-Band Polarimetric Interferometric SAR Data in Estimating Boreal Forest above-Ground Biomass. IEEE Trans. Geosci. Remote Sens. 2012, 50, 714–726. [Google Scholar] [CrossRef]
- Khati, U.; Ferro-Famil, L.; Singh, G. First Demonstration of Space-Borne Tomosar Using Terrasar-x/Tandem-x Full-Polarimetric Acquisitions. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5275–5276. [Google Scholar] [CrossRef]
- Cloude, S. Multibaseline Polarization Coherence Tomography. Sci. Appl. SAR Polarim. Polarim. Interferom. 2007, 644, 8. [Google Scholar]
- Choi, C.; Pardini, M.; Papathanassiou, K. Quantification of Horizontal Forest Structure from High Resolution TanDEM-X Interferometric Coherences. In Proceedings of the IGARSS 2018 - 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 376–379. [Google Scholar] [CrossRef]
- Pulella, A.; Bispo, P.C.; Pardini, M.; Kugler, F.; Cazcarra, V.; Tello, M.; Papathanassiou, K.; Balzter, H.; Rizaev, I.; Santos, M.N.; et al. Tropical Forest Structure Observation with TanDEM-X Data. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 918–921. [Google Scholar] [CrossRef] [Green Version]
- Kugler, F.; Schulze, D.; Hajnsek, I.; Pretzsch, H.; Papathanassiou, K.P. TanDEM-X Pol-InSAR Performance for Forest Height Estimation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6404–6422. [Google Scholar] [CrossRef]
- Soja, M.J.; Baker, S.C.; Jordan, G.J.; Lucieer, A.; Musk, R.; Ulander, L.M.H.; Williams, M.L.; White, R.J. Unveiling the Complex Structure of Tasmanian Temperate Forests with Model-Based TanDEM-X Tomography. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 383–386. [Google Scholar] [CrossRef]
- Pardini, M.; Torano-Caicoya, A.; Kugler, F.; Papathanassiou, K. Estimating and Understanding Vertical Structure of Forests from Multibaseline TanDEM-X Pol-InSAR Data. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 4344–4347. [Google Scholar] [CrossRef] [Green Version]
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric Optimisation in Radar Interferometry. Electron. Lett. 1997, 33, 1176–1178. [Google Scholar] [CrossRef]
- Yamashita, T.; Yamashita, K.; Kamimura, R. A Stepwise AIC Method for Variable Selection in Linear Regression. Commun. Stat. Theory Methods 2007, 36, 2395–2403. [Google Scholar] [CrossRef]
- Tomppo, E.; Olsson, H.; Ståhl, G.; Nilsson, M.; Hagner, O.; Katila, M. Combining National Forest Inventory Field Plots and Remote Sensing Data for Forest Databases. Remote Sens. Environ. 2008, 112, 1982–1999. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Gleason, C.J.; Im, J. Forest Biomass Estimation from Airborne LiDAR Data Using Machine Learning Approaches. Remote Sens. Environ. 2012, 125, 80–91. [Google Scholar] [CrossRef]
- Mohammadi, J. Improving in Estimation of Some Forest Structure Quantitative Characteristics by Combining the Lidar and Digital Aerial Images in Shastkalateh Hardwood Forests of Gorgan. Ph.D Thesis, Gorgan University of Agricultural Sciences and Natural Resources, Gorgan, Iran, 2012. [Google Scholar]
- Lexerød, N.L.; Eid, T. An Evaluation of Different Diameter Diversity Indices Based on Criteria Related to Forest Management Planning. For. Ecol. Manage. 2006, 222, 17–28. [Google Scholar] [CrossRef]
- Latifi, H. Characterizing Forest Structure by Means of Remote Sensing: A Review. In Remote Sensing—Advanced Techniques and Platforms; IntechOpen: London, UK, 2012. [Google Scholar] [CrossRef] [Green Version]
- Uotila, A.; Kouki, J.; Kontkanen, H.; Pulkkinen, P. Assessing the Naturalness of Boreal Forests in Eastern Fennoscandia. For. Ecol. Manage. 2002, 161, 257–277. [Google Scholar] [CrossRef]
- McElhinny, C.; Gibbons, P.; Brack, C.; Bauhus, J. Forest and Woodland Stand Structural Complexity: Its Definition and Measurement. For. Ecol. Manage. 2005, 218, 1–24. [Google Scholar] [CrossRef]
- Motz, K.; Sterba, H.; Pommerening, A. Sampling Measures of Tree Diversity. For. Ecol. Manage. 2010, 260, 1985–1996. [Google Scholar] [CrossRef]
- Winter, S.; Chirici, G.; McRoberts, R.E.; Hauk, E.; Tomppo, E. Possibilities for Harmonizing National Forest Inventory Data for Use in Forest Biodiversity Assessments. Forestry 2008, 81, 33–44. [Google Scholar] [CrossRef] [Green Version]
- Winter, S.; Böck, A.; McRoberts, R.E. Uncertainty of Large-Area Estimates of Indicators of Forest Structural Gamma Diversity: A Study Based on National Forest Inventory Data. For. Sci. 2012, 58, 284–293. [Google Scholar] [CrossRef]
- Karl, K.; Pfeifer, N. Determination of Terrain Models in Wooded Areas with Airborne Laser Scanner Data. J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar]
- Aulinger, T.; Mette, T.; Papathanassiou, K.P.; Hajnsek, I.; Heurich, M.; Krzystek, P. Validation of Heights from Interferometric SAR and Lidar over the Temperate Forest Site Nationalpark Bayerischer Wald; ESA Special Publication: Frascati, Italy, 2005; pp. 67–72. [Google Scholar]
- Hajnsek, I.; Kugler, F.; Lee, S.K.; Papathanassiou, K.P. Tropical-Forest-Parameter Estimation by Means of Pol-InSAR: The INDREX-II Campaign. IEEE Trans. Geosci. Remote Sens. 2009, 47, 481–493. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Three-Stage Inversion Process for Polarimetric SAR Interferometry. IEE Proc. Radar Sonar Navig. 2003, 150, 125–134. [Google Scholar] [CrossRef] [Green Version]
- Cloude, S.R.; Papathanassiou, K.P. Forest Vertical Structure Estimation Using Coherence Tomography. Int. Geosci. Remote Sens. Symp. 2008, 5, 275–278. [Google Scholar] [CrossRef]
- Cloude, S.R. Polarisation: Applications in Remote Sensing; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Albinet, C.; Borderies, P.; Hamadi, A.; Dubois-Fernandez, P.; Koleck, T.; Angelliaume, S. High-Resolution Vertical Polarimetric Imaging of Pine Forests. Radio Sci. 2014, 49, 231–241. [Google Scholar] [CrossRef]
- Cazcarra-Bes, V.; Tello-Alonso, M.; Fischer, R.; Heym, M.; Papathanassiou, K. Monitoring of Forest Structure Dynamics by Means of L-Band SAR Tomography. Remote Sens. 2017, 9, 1229. [Google Scholar] [CrossRef] [Green Version]
- Constantine, W.; Hesterberg, T. Splus2R: Supplemental S-PLUS Functionality in R; R Package Version 1.3-3. 2021. Available online: https://cran.r-project.org/web/packages/splus2R/index.html (accessed on 15 January 2023).
- McRoberts, R.E. Estimating Forest Attribute Parameters for Small Areas Using Nearest Neighbors Techniques. For. Ecol. Manage. 2012, 272, 3–12. [Google Scholar] [CrossRef]
- Zhou, G.; Xu, X.; Du, H.; Ge, H.; Shi, Y.; Zhou, Y. Estimating Aboveground Carbon of Moso Bamboo Forests Using the K Nearest Neighbors Technique and Satellite Imagery. Photogramm. Eng. Remote Sensing 2011, 77, 1123–1131. [Google Scholar] [CrossRef]
- Gjertsen, A.K. Accuracy of Forest Mapping Based on Landsat TM Data and a KNN-Based Method. Remote Sens. Environ. 2007, 110, 420–430. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 297, 273–297. [Google Scholar] [CrossRef]
- Sammut, C.; Webb, G.I. Encyclopedia of Machine Learning; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Brede, B.; Terryn, L.; Barbier, N.; Bartholomeus, H.M.; Bartolo, R.; Calders, K.; Derroire, G.; Krishna Moorthy, S.M.; Lau, A.; Levick, S.R.; et al. Non-Destructive Estimation of Individual Tree Biomass: Allometric Models, Terrestrial and UAV Laser Scanning. Remote Sens. Environ. 2022, 280, 113180. [Google Scholar] [CrossRef]
- Zhu, J.; Huang, Z.; Sun, H.; Wang, G. Mapping Forest Ecosystem Biomass Density for Xiangjiang River Basin by Combining Plot and Remote Sensing Data and Comparing Spatial Extrapolation Methods. Remote Sens. 2017, 9, 241. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A Survey of Remote Sensing-Based Aboveground Biomass Estimation Methods in Forest Ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Li, X.; Ye, Z.; Long, J.; Zheng, H.; Lin, H. Inversion of Coniferous Forest Stock Volume Based on Backscatter and InSAR Coherence Factors of Sentinel-1 Hyper-Temporal Images and Spectral Variables of Landsat 8 OLI. Remote Sens. 2022, 14, 2754. [Google Scholar] [CrossRef]
- Vandekerkhove, K.; van Den Meersschaut, D. Development of a Stand-Scale Forest Biodiversity Index Based on the State Forest Inventory. In Integrated Tools for Natural Resources Inventories in the 21st Century; U.S. Dept. of Agriculture, Forest Service: Washington, DC, USA; North Central Forest Experiment Station: Saint Paul, MN, USA, 2000; pp. 340–349. [Google Scholar]
- Zenner, E.K.; Hibbs, D.E. A New Method for Modeling the Heterogeneity of Forest Structure. For. Ecol. Manage. 2000, 129, 75–87. [Google Scholar] [CrossRef]
- Tello, M.; Cazcarra-Bes, V.; Pardini, M.; Papathanassiou, K. Forest Structure Characterization from SAR Tomography at L-Band. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3402–3414. [Google Scholar] [CrossRef] [Green Version]
- Mura, M.; McRoberts, R.E.; Chirici, G.; Marchetti, M. Estimating and Mapping Forest Structural Diversity Using Airborne Laser Scanning Data. Remote Sens. Environ. 2015, 170, 133–142. [Google Scholar] [CrossRef]
- Monnet, J.; Mermin, E.; Chanussot, J. Using Airborne Laser Scanning to Assess Forest Protection Function against Rockfall to Cite This Version. In Proceedings of the Interpraevent International Symposium in Pacific Rim, Taipei, Taiwan, 26–30 April 2010. [Google Scholar]





| Variable | Minimum | 1st Quartile | Mean | 3rd Quartile | Median | Maximum |
|---|---|---|---|---|---|---|
| Basal-area-weighted mean dbh (m) | 0.11 | 0.43 | 0.52 | 0.54 | 0.64 | 1.15 |
| Basal-area-weighted mean height (m) | 7.20 | 21.09 | 23.32 | 23.23 | 25.37 | 33.00 |
| Mean volume (m3) | 0.45 | 18.15 | 26.45 | 33.46 | 24.94 | 71.71 |
| Standard deviation of dbh (cm) | 1.62 | 13.93 | 18.27 | 22.26 | 17.54 | 39.90 |
| Number of trees (n) | 4.00 | 15.00 | 21.30 | 25.00 | 20.00 | 61.00 |
| Parameter | Description/Formula |
|---|---|
| The ratio of first envelope span to the relative reflectivity at h2 | |
| The integral of relative reflectivity multiplied by the corresponding height in the first envelope | |
| Maximum probability of fitted Gaussian function | |
| Mean of fitted Gaussian function | |
| Standard deviation of fitted Gaussian function | |
| Reciprocal of relative reflectivity summation for the first envelope | |
| Reciprocal of relative reflectivity summation for the second envelope | |
| The ratio of P6 to P7 | |
| The ratio of relative reflectivity summation in h1 and h2 to h2 and h3 | |
| The integral of relative reflectivity multiplied by the corresponding height in the whole curve | |
| Height corresponding to power loss in a ranging from h2 to h3 with power loss value from 0 to 1 optimized by the lidar true height value | |
| Number of reflectivity peaks with span=15 | |
| The 3D distribution of reflectivity peaks |
| Attribute | |||||||||
| 0.07 | 0.07 | 0.14 | 0.07 | 0.40 | −0.03 | 0.17 | −0.09 | −0.02 | |
| 0.10 | 0.10 | 0.09 | 0.14 | 0.05 | 0.02 | −0.07 | 0.12 | 0.04 | |
| Attribute | |||||||||
| −0.08 | −0.16 | 0.01 | −0.02 | −0.16 | 0.17 | 0.40 | 0.25 | 0.26 | |
| 0.10 | 0.04 | −0.03 | 0.00 | 0.21 | −0.23 | −0.33 | −0.22 | 0.12 |
| Algorithm | Tuning Parameters | RMSE (cm) | RMSE (%) | MAE (cm) | MAE (%) | Pseudo-R2 (R2*) | |
|---|---|---|---|---|---|---|---|
| MLR | AIC = 1085.23 | 6.05 | 33.09 | 4.64 | 25.40 | 0.25 | |
| k-NN | Euclidian | k = 13 | 6.16 | 33.72 | 4.79 | 26.15 | 0.20 |
| Euclidian squared | k = 20 | 6.19 | 33.89 | 4.80 | 26.26 | 0.19 | |
| Manhattan | k = 18 | 5.99 | 32.80 | 4.69 | 25.69 | 0.25 | |
| Chebyshev | k = 19 | 6.29 | 34.43 | 4.88 | 26.73 | 0.16 | |
| RF | Default number of trees = 500 | F = 2 | 6.02 | 32.97 | 4.71 | 25.77 | 0.24 |
| F = 3 | 6.00 | 32.84 | 4.68 | 25.64 | 0.25 | ||
| F = 4 | 6.00 | 32.85 | 4.70 | 25.72 | 0.25 | ||
| F = 5 | 6.02 | 32.94 | 4.71 | 25.77 | 0.24 | ||
| F = 6 | 5.99 | 32.80 | 4.70 | 25.71 | 0.25 | ||
| SVR | Linear | C = 0.50 | 10.55 | 57.74 | 7.68 | 42.04 | 0.14 |
| Polynomial degree 2 | C = 1.00 | 6.05 | 33.13 | 4.65 | 25.46 | 0.24 | |
| Polynomial degree 3 | C = 1.00 | 6.06 | 33.16 | 4.64 | 25.40 | 0.25 | |
| Radial base function | C = 0.25 | 6.13 | 33.56 | 4.68 | 25.59 | 0.21 | |
| Sigmoid | C = 0.25 | 6.05 | 33.09 | 4.65 | 25.44 | 0.24 | |
| Algorithm | Tuning Parameters | RMSE (n ha−1) | RMSE (%) | MAE (n ha−1) | MAE (%) | Pseudo-R2 (R2*) | |
|---|---|---|---|---|---|---|---|
| MLR | AIC = 1344.05 | 94.91 | 44.56 | 69.19 | 32.49 | 0.16 | |
| k-NN | Euclidian | k = 13 | 90.10 | 42.30 | 65.61 | 30.81 | 0.19 |
| Euclidian squared | k = 16 | 90.53 | 42.50 | 65.89 | 30.94 | 0.18 | |
| Manhattan | k = 18 | 88.53 | 41.56 | 64.56 | 30.31 | 0.22 | |
| Chebyshev | k = 19 | 91.32 | 42.87 | 65.97 | 30.97 | 0.17 | |
| RF | Default number of trees = 500 | F = 2 | 91.61 | 43.01 | 67.49 | 31.69 | 0.17 |
| F = 3 | 91.42 | 42.92 | 67.09 | 31.50 | 0.18 | ||
| F = 4 | 91.70 | 43.05 | 67.41 | 31.65 | 0.18 | ||
| F = 5 | 91.76 | 43.08 | 67.16 | 31.53 | 0.18 | ||
| F = 6 | 91.64 | 43.02 | 67.30 | 31.60 | 0.18 | ||
| SVR | Linear | C = 0.25 | 108.07 | 50.74 | 76.30 | 35.82 | 0.11 |
| Polynomial degree 2 | C = 0.50 | 91.57 | 42.99 | 65.63 | 30.83 | 0.18 | |
| Polynomial degree 3 | C = 0.50 | 92.33 | 43.35 | 65.76 | 30.88 | 0.17 | |
| Radial base function | C = 0.25 | 90.93 | 42.69 | 65.08 | 30.55 | 0.19 | |
| Sigmoid | C = 0.50 | 92.46 | 43.42 | 67.06 | 31.49 | 0.16 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poorazimy, M.; Shataee, S.; Aghababaei, H.; Tomppo, E.; Praks, J. First Demonstration of Space-Borne Polarization Coherence Tomography for Characterizing Hyrcanian Forest Structural Diversity. Remote Sens. 2023, 15, 555. https://doi.org/10.3390/rs15030555
Poorazimy M, Shataee S, Aghababaei H, Tomppo E, Praks J. First Demonstration of Space-Borne Polarization Coherence Tomography for Characterizing Hyrcanian Forest Structural Diversity. Remote Sensing. 2023; 15(3):555. https://doi.org/10.3390/rs15030555
Chicago/Turabian StylePoorazimy, Maryam, Shaban Shataee, Hossein Aghababaei, Erkki Tomppo, and Jaan Praks. 2023. "First Demonstration of Space-Borne Polarization Coherence Tomography for Characterizing Hyrcanian Forest Structural Diversity" Remote Sensing 15, no. 3: 555. https://doi.org/10.3390/rs15030555
APA StylePoorazimy, M., Shataee, S., Aghababaei, H., Tomppo, E., & Praks, J. (2023). First Demonstration of Space-Borne Polarization Coherence Tomography for Characterizing Hyrcanian Forest Structural Diversity. Remote Sensing, 15(3), 555. https://doi.org/10.3390/rs15030555