A Compact High-Order Finite-Difference Method with Optimized Coefficients for 2D Acoustic Wave Equation
Abstract
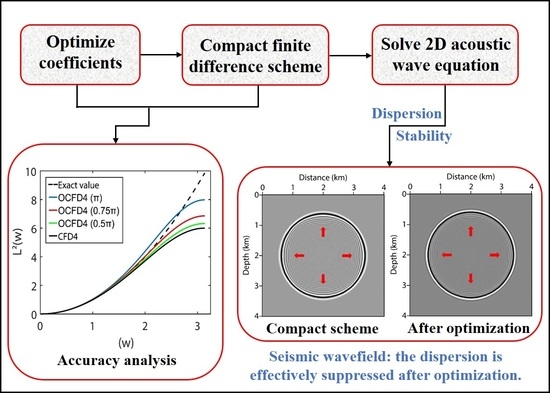
:1. Introduction
2. Theory and Methods
2.1. Tridiagonal Compact Finite-Difference Schemes for 2D Acoustic Wave Equation
2.2. Optimization of Compact Finite-Difference Coefficients
2.3. Dispersion Analysis and Stability Analysis
3. Numerical Examples
3.1. Homogeneous Model
3.2. Marmousi Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A



Appendix B
| Schemes | Constraints | Order | Optimization Conditions |
|---|---|---|---|
| CFD4 | Equations (3) and (4) | fourth | / |
| OCFD4 | Equation (3) | second | |
| CFD6 | Equations (3)–(5) | sixth | / |
| OCFD6 | Equations (3) and (4) | fourth | |
| OCFD6_2 | Equation (3) | second | |
| CFD8 | Equations (3)–(6) | eighth | / |
| OCFD8 | Equations (3)–(5) | sixth | |
| OCFD8_4 | Equations (3) and (4) | fourth | |
| OCFD8_2 | Equation (3) | second |
References
- Li, X.; Yao, G.; Niu, F.; Wu, D.; Liu, N. Waveform inversion of seismic first arrivals acquired on irregular surface. Geophysics 2022, 87, 1MJ-V246. [Google Scholar] [CrossRef]
- Yao, G.; Wu, B.; da Silva, N.V.; Debens, H.A.; Wu, D.; Cao, J. Least-squares reverse-time migration with a multiplicative Cauchy constraint. Geophysics 2022, 87, 1MJ-V246. [Google Scholar] [CrossRef]
- Han, Y.; Wu, B.; Yao, G.; Ma, X.; Wu, D. Eliminate time dispersion of seismic wavefield simulation with semi-supervised deep learning. Energies 2022, 15, 7701. [Google Scholar] [CrossRef]
- Baysal, E.; Kosloff, D.D.; Sherwood, J.W. Reverse time migration. Geophysics 1983, 48, 1514–1524. [Google Scholar] [CrossRef] [Green Version]
- Abubakar, A.; Pan, G.; Li, M.; Zhang, L.; Habashy, T.M.; Berg, P.M.V.D. Three-dimensional seismic full-waveform inversion using the finite-difference contrast source inversion method. Geophys. Prospect. 2011, 59, 874–888. [Google Scholar] [CrossRef]
- Alford, R.M.; Kelly, K.R.; Boore, D.M. Accuracy of finite-difference modeling of the acoustic wave equation. Geophysics 1974, 39, 834–842. [Google Scholar] [CrossRef] [Green Version]
- Kelly, K.R.; Ward, R.W.; Treitel, S.; Alford, R.M. Synthetic seismograms: A finite difference approach. Geophysics 1976, 41, 2–27. [Google Scholar] [CrossRef]
- Virieux, J. SH-wave propagation in heterogeneous media: Velocity-stress finite-difference method. Geophysics 1984, 49, 1933–1942. [Google Scholar] [CrossRef]
- Virieux, J. P-SV wave propagation in heterogeneous media velocity-stress finite-difference method. Geophysics 1984, 51, 889–901. [Google Scholar] [CrossRef]
- Marfurt, K.J. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics 1984, 49, 533–549. [Google Scholar] [CrossRef]
- Kay, I.; Krebes, E.S. Applying finite-element analysis to the memory variable formulation of wave propagation in anelastic media. Geophysics 1999, 64, 300–307. [Google Scholar] [CrossRef]
- Komatitsch, D.; Vilotte, J.P. The spectral-element method: An efficient tool to simulate the seismic response of 2-D and 3-D geological structures. Bull. Seismol. Soc. Am. 1998, 88, 368–392. [Google Scholar] [CrossRef]
- Komatitsch, D.; Tromp, J. Introduction to the spectral-element method for 3-D seismic wave propagation. Geophys. J. Int. 1999, 139, 806–822. [Google Scholar] [CrossRef] [Green Version]
- Komatitsch, D.; Tromp, J. Spectral-element simulations of global seismic wave propagation—Part I: Validation. Geophys. J. Int. 2002, 149, 390–412. [Google Scholar] [CrossRef]
- Komatitsch, D.; Tromp, J. Spectral-element simulations of global seismic wave propagation—Part II: 3-D models, oceans, rotation, and self-gravitation. Geophys. J. Int. 2002, 150, 303–318. [Google Scholar] [CrossRef]
- Sánchez-Sesma, F.J.; Esquivel, J. Ground motion on alluvial valleys under incident plane SH waves. Bull. Seismol. Soc. Am. 1979, 69, 1107–1120. [Google Scholar] [CrossRef]
- Gaffet, S.; Bouchon, M. Source location and valley shape effects on the P-SV displacement field using a boundary integral equation-discrete wavenumber representation method. Geophys. J. Int. 1991, 106, 341–355. [Google Scholar] [CrossRef] [Green Version]
- Sánchez-Sesma, F.J.; Campillo, M. Diffraction of P, SV, and Raileigh waves by topographic features: A boundary integral formulation. Bull. Seismol. Soc. Am. 1991, 81, 2234–2253. [Google Scholar] [CrossRef]
- Bouchon, M.; Schultz, C.A.; Toksoz, M.N. A fast implementation of boundary integral equation methods to calculate the propagation of seismic waves in laterally varying layered medium. Bull. Seismol. Soc. Am. 1995, 85, 1679–1687. [Google Scholar] [CrossRef]
- Fornberg, B. The pseudospectral method: Comparisons with finite differences for the elastic wave equation. Geophysics 1987, 52, 483–501. [Google Scholar] [CrossRef]
- Fornberg, B. The pseudospectral method: Accurate representation of interfaces in elastic wave calculations. Geophysics 1988, 53, 625–637. [Google Scholar] [CrossRef]
- Faccioli, E.; Maggio, F.; Paolucci, R.; Quarteroni, A. 2D and 3D elastic wave propagation by a pseudo-spectral domain decomposition method. J. Seismol. 1997, 1, 237–251. [Google Scholar] [CrossRef]
- Dormy, E.; Tarantola, A. Numerical simulation of elastic wave propagation using a finite volume method. J. Geophys. Res. 1995, 100, 2123–2133. [Google Scholar] [CrossRef]
- Robertsson, J.O.A. A numerical free-surface condition for elastic/viscoelastic finite-difference modeling in the presence of topography. Geophysics 1996, 61, 1921–1934. [Google Scholar] [CrossRef]
- Das, S.; Liao, W.; Gupta, A. An efficient fourth-order low dispersive finite difference scheme for a 2-D acoustic wave equation. J. Comput. Appl. Math. 2014, 258, 151–167. [Google Scholar] [CrossRef]
- Ren, Y.; Huang, J.; Yong, P.; Liu, M.; Cui, C.; Yang, M. Optimized staggered-grid finite-difference operators using window functions. Appl. Geophys. 2018, 15, 253–260. [Google Scholar] [CrossRef]
- Yang, D.H.; Wang, N.; Chen, S.; Song, G.J. An explicit method based on the implicit Runge–Kutta algorithm for solving the wave equations. Bull. Seismol. Soc. Am. 2009, 99, 3340–3354. [Google Scholar] [CrossRef]
- Orszag, S.A.; Israeli, M. Numerical simulation of viscous incompressible flows. Annu. Rev. Fluid Mech. 1974, 6, 281–318. [Google Scholar] [CrossRef]
- Hirsh, R.S. Higher order accurate difference solutions of fluid mechanics problems by a compact differencing technique. J. Comput. Phys. 1975, 19, 90–109. [Google Scholar] [CrossRef]
- Adam, Y. A Hermitian finite difference method for the solution of parabolic equations. Comput. Math. Appl. 1975, 1, 393–406. [Google Scholar] [CrossRef]
- Lele, S.K. Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]
- Mahesh, K. A family of high order finite difference schemes with good spectral resolution. J. Comput. Phys. 1998, 145, 332–358. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Seo, Y. A new compact spectral scheme for turbulence simulations. J. Comput. Phys. 2002, 183, 438–469. [Google Scholar] [CrossRef]
- Chu, P.C.; Fan, C. A three-point combined compact difference scheme. J. Comput. Phys. 1998, 140, 370–399. [Google Scholar] [CrossRef] [Green Version]
- Sengupta, T.K.; Lakshmanan, V.; Vijay, V.V.S.N. A new combined stable and dispersion relation preserving compact scheme for non-periodic problems. J. Comput. Phys. 2009, 228, 3048–3071. [Google Scholar] [CrossRef]
- Mohebbi, A.; Abbaszadeh, M. Compact finite difference scheme for the solution of time fractional advection-dispersion equation. Numer Algorithms. 2013, 63, 431–452. [Google Scholar] [CrossRef]
- Geodheer, W.J.; Potters, J.H.H.M. A compact finite difference scheme on a non-equidistant mesh. J. Comput. Phys. 1985, 61, 269–279. [Google Scholar] [CrossRef]
- Shukla, R.K.; Zhong, X. Derivation of high-order compact finite difference schemes for non-uniform grid using polynomial interpolation. J. Comput. Phys. 2005, 204, 404–429. [Google Scholar] [CrossRef]
- Yang, D.; Wang, S.; Zhang, Z.; Teng, J. N-times absorbing boundary conditions for compact finite-difference modeling of acoustic and elastic wave propagation in the 2D TI medium. Bull. Seismol. Soc. Am. 2003, 93, 2389–2401. [Google Scholar] [CrossRef]
- Du, Q.; Li, B.; Hou, B. Numerical modeling of seismic wavefields in transversely isotropic media with a compact staggered-grid finite difference scheme. Appl. Geophys. 2009, 6, 42–49. [Google Scholar] [CrossRef]
- Kosloff, D.; Pestana, R.C.; Tal-Ezer, H. Acoustic and elastic numerical wave simulations by recursive spatial derivative operators. Geophysics 2010, 75, T167–T174. [Google Scholar] [CrossRef]
- Chu, C.; Stoffa, P.L. Frequency domain modeling using implicit spatial finite difference operators. In SEG Technical Program Expanded Abstracts 2010; Society of Exploration Geophysicists: Houston, TX, USA, 2010; pp. 3076–3080. [Google Scholar] [CrossRef]
- Liu, Y. An optimal 5-point scheme for frequency-domain scalar wave equation. J. Appl. Geophys. 2014, 108, 19–24. [Google Scholar] [CrossRef]
- Liao, W. On the dispersion, stability and accuracy of a compact higher-order finite difference scheme for 3D acoustic wave equation. J. Comput. Appl. Math. 2014, 270, 571–583. [Google Scholar] [CrossRef]
- Li, K.; Liao, W. An efficient and high accuracy finite-difference scheme for the acoustic wave equation in 3D heterogeneous media. J. Comput. Sci. 2020, 40, 101063. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.W.; Lee, D.J. Optimized compact finite difference schemes with maximum resolution. AIAA 1996, 34, 887–893. [Google Scholar] [CrossRef] [Green Version]
- Tam, C.K.W.; Webb, J.C. Dispersion–relation–preserving schemes for computational aeroacoustics. AIAA 1992, 1, 92-02-033. [Google Scholar]
- Liu, Z.; Huang, Q.; Zhao, Z.; Yuan, J. Optimized compact finite difference schemes with high accuracy and maximum resolution. Int. J. Aeroacoustics 2008, 7, 123–146. [Google Scholar] [CrossRef]
- Yu, C.H.; Wang, D.; He, Z.; Pähtz, T. An optimized dispersion-relation-preserving combined compact difference scheme to solve advection equations. J. Comput. Phys. 2015, 300, 92–115. [Google Scholar] [CrossRef] [Green Version]
- Venutelli, M. New optimized fourth-order compact finite difference schemes for wave propagation phenomena. Appl. Numer. Math. 2014, 87, 53–73. [Google Scholar] [CrossRef]
- Huang, J.; Yang, J.; Liao, W.; Wang, X.; Li, Z. Common-shot Fresnel beam migration based on wave-field approximation in effective vicinity under complex topographic conditions. Geophys. Prospect. 2016, 64, 554–570. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, L.-Y.; Zhang, L.X.; Wei, W.; Guan, X. Finite difference modeling of ultrasonic propagation (coda waves) in digital porous cores with un-split convolutional PML and rotated staggered grid. J. Appl. Geophys. 2014, 104, 75–89. [Google Scholar] [CrossRef]
- Hou, W.; Fu, L.-Y.; Carcione, J.M.; Wang, Z.W.; Wei, J. Simulation of thermoelastic waves based on the Lord-Shulman theory. Geophysics 2021, 86, T155–T164. [Google Scholar] [CrossRef]
- Zhang, L.X.; Fu, L.-Y.; Pei, Z.L. Finite difference modeling of Biot’s poroelastic equations with unsplit convolutional PML and rotated staggered grid. Chin. J. Geophys. 2010, 53, 2470–2483. [Google Scholar] [CrossRef]
- Yang, H.; Fu, L.-Y.; Fu, B.-Y.; Du, Q. Poro-acoustoelasticity finite-difference simulation of elastic wave propagation in prestressed porous media. Geophysics 2022, 87, T329–T345. [Google Scholar] [CrossRef]
- Yang, L.; Yan, H.Y.; Liu, H. Optimal staggered-grid finite-difference schemes based on the minimax approximation method with the Remez algorithm. Geophysics 2017, 82, T27–T42. [Google Scholar] [CrossRef]
- Yong, P.; Huang, J.P.; Li, Z.C.; Liao, W.Y.; Qu, L.P.; Li, Q.Y.; Liu, P.J. Optimized equivalent staggered-grid FD method for elastic wave modelling based on plane wave solutions. Geophys. J. Int. 2017, 208, 1157–1172. [Google Scholar] [CrossRef]
- Jin, K.; Huang, J.P.; Zou, Q.; Wang, Z.; Tong, S.; Liu, B.; Hu, Z. Optimization of staggered grid finite-difference coefficients based on conjugate gradient method. J. Seism. Explor. 2021, 31, 33–52. [Google Scholar]
- Haras, Z.; Ta’asan, S. Finite difference schemes for long–time integration. J. Comput. Phys. 1994, 114, 265–279. [Google Scholar] [CrossRef]












| Schemes | Constraints | Order | ||||
|---|---|---|---|---|---|---|
| CFD4 | Equations (3) and (4) | fourth | 0.1 | 1.2 | 0 | 0 |
| CFD6 | Equations (3)–(5) | sixth | 0.181818 | 1.090909 | 0.061818 | 0 |
| CFD8 | Equations (3)–(6) | eighth | 0.236842 | 0.967105 | 0.536842 | −0.030263 |
| Schemes | Constraints | Order | Integral Limit | ||||
|---|---|---|---|---|---|---|---|
| OCFD4 | Equation (3) | second | π | 0.166054 | 1.332109 | 0 | 0 |
| 0.75π | 0.131511 | 1.263021 | 0 | 0 | |||
| 0.5π | 0.112531 | 1.225063 | 0 | 0 | |||
| OCFD6 | Equations (3) and (4) | fourth | π | 0.277327 | 0.963564 | 0.591090 | 0 |
| 0.75π | 0.224304 | 1.034262 | 0.414346 | 0 | |||
| 0.5π | 0.198053 | 1.069262 | 0.326844 | 0 | |||
| OCFD8 | Equations (3)–(5) | sixth | π | 0.332545 | 0.751775 | 0.996214 | −0.082900 |
| 0.75π | 0.277486 | 0.875656 | 0.731933 | −0.052617 | |||
| 0.5π | 0.251903 | 0.933217 | 0.609136 | −0.038547 |
| Schemes | CFL Number | Schemes | CFL Number | Schemes | CFL Number |
|---|---|---|---|---|---|
| CFD4 | 0.817 | CFD6 | 0.764 | CFD8 | 0.750 |
| OCFD4 (0.5π) | 0.795 | OCFD6 (0.5π) | 0.752 | OCFD8 (0.5π) | 0.745 |
| OCFD4 (0.75π) | 0.764 | OCFD6 (0.75π) | 0.730 | OCFD8 (0.75π) | 0.735 |
| OCFD4 (π) | 0.708 | OCFD6 (π) | 0.680 | OCFD8 (π) | 0.708 |
| Schemes | Recording Time (s) | Computing Time (s) | Recording Time (s) | Computing Time (s) | Recording Time (s) | Computing Time (s) |
|---|---|---|---|---|---|---|
| CFD4 | 5 | 36.7 | 10 | 73.2 | 20 | 145.6 |
| CFD6 | 5 | 70.9 | 10 | 142.0 | 20 | 283.7 |
| CFD8 | 5 | 108.5 | 10 | 217.4 | 20 | 433.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Huang, J.; Fu, L.-Y.; Peng, W.; Song, C.; Han, J. A Compact High-Order Finite-Difference Method with Optimized Coefficients for 2D Acoustic Wave Equation. Remote Sens. 2023, 15, 604. https://doi.org/10.3390/rs15030604
Chen L, Huang J, Fu L-Y, Peng W, Song C, Han J. A Compact High-Order Finite-Difference Method with Optimized Coefficients for 2D Acoustic Wave Equation. Remote Sensing. 2023; 15(3):604. https://doi.org/10.3390/rs15030604
Chicago/Turabian StyleChen, Liang, Jianping Huang, Li-Yun Fu, Weiting Peng, Cheng Song, and Jiale Han. 2023. "A Compact High-Order Finite-Difference Method with Optimized Coefficients for 2D Acoustic Wave Equation" Remote Sensing 15, no. 3: 604. https://doi.org/10.3390/rs15030604
APA StyleChen, L., Huang, J., Fu, L. -Y., Peng, W., Song, C., & Han, J. (2023). A Compact High-Order Finite-Difference Method with Optimized Coefficients for 2D Acoustic Wave Equation. Remote Sensing, 15(3), 604. https://doi.org/10.3390/rs15030604