1. Introduction
In recent years, image-based modeling based on oblique aerial images acquired by unmanned aerial vehicle (UAVs) has been widely used for urban planning, infrastructure monitoring, environmental monitoring, emergency response, and cultural heritage conservation [
1,
2,
3,
4,
5,
6,
7,
8]. The core techniques of image-based 3D reconstruction include image matching, structure from motion (SfM), and dense matching. Image matching extracts feature points from images and matches the feature points using similarity measures [
9]. Tie points are then determined by filtering the matched feature points based on the fundamental matrix with a random sample consensus (RANSAC) framework [
10]. Tracks are generated by connecting the geometrically consistent tie points. SfM is used to fully automatically orient the images and reconstruct a sparse model of a scene. The poses of images, spatial positions of tracks, and calibration parameters of cameras are globally optimized with bundle block adjustment [
11]. Based on the sparse reconstruction, dense matching extracts dense correspondence between overlapping images and generates depth maps [
12]. A dense point cloud is then derived by fusing the depth maps. Finally, a photorealistic 3D model is obtained by meshing the dense cloud and texturing the mesh with the acquired images. This pipeline works well in 3D modelling based on small-sized datasets. With fast-growing images, SfM has encountered challenges in terms of efficiency. [
13].
Incremental SfM is well known in early studies for the reconstruction of landmarks based on photos collected from the Internet [
14,
15]. The incremental SfM firstly reconstructs an initial stereo model using a selected image pair, and then grows the model by iteratively adding new images and globally optimizing all parameters. The time complexity of the initial incremental SfM methodology is commonly known to be
O(
n4) for
n images, which impedes the application of the initial incremental SfM on large datasets. Many studies have been proposed to reduce the complexity of incremental SfM. A methodology based on conjugate gradients was proposed in [
16] to improve the efficiency of solving large-scale bundle problems. Experiments showed that the truncated Newton method, paired with relatively simple preconditioners, achieved a significant efficiency improvement on datasets containing tens of thousands of images. The incremental SfM pipeline was extended to reconstruct city-scale image collections [
17]. The proposed pipeline was built on distributed algorithms for image matching and SfM. Each stage of the pipeline was fully parallelized. Experiments showed that the proposed pipeline was able to reconstruct a large scene with more than a hundred thousand unstructured images in less than a day. A novel methodology was proposed to improve the efficiency of the incremental SfM in [
18]. A preemptive matching strategy was proposed to speed up the image matching process. Moreover, the multicore bundle block adjustment algorithm proposed in [
19] was used to improve the efficiency of SfM. Experiments on large photo collections showed that the time complexity of the proposed pipeline was close to
O(
n).
Hierarchical SfM is a natural extension of the incremental strategy. It adopts the divide-and-conquer approach to improve the efficiency of SfM. A variety of hierarchical methodologies have been proposed. An out-of-core bundle adjustment was proposed for large-scale 3D reconstruction [
20]. The proposed approach partitioned the cameras and points into submaps by performing graph-cut inference on the graph built from connected images and points. The submaps were reconstructed in parallel, and merged globally afterwards. The proposed methodology performed well on synthetic and real datasets. A hierarchical approach based on skeletal graphs was proposed for efficient SfM [
21]. The proposed approach computed a small skeletal set of images using maximum leaf spanning tree. Then, it reconstructed the scene based on the skeletal set, and any remaining images were added using pose estimation. Experiments on datasets containing thousands of images showed that the methodology achieved dramatic speedups compared to the traditional incremental SfM. A hierarchical pipeline based on the cluster tree model was proposed [
22,
23,
24]. Images of a scene were firstly organized to a hierarchical cluster tree. Then, the pipeline reconstructed the scene along the tree from the leaves to the root. Experiments on several datasets containing hundreds of images showed that increased speedup was achieved compared to Bundler and VisualSFM. A multistage approach for SfM reconstruction was proposed [
25]. The approach firstly reconstructed a coarse model of a scene using a fraction of feature points. The coarse model was then completed by registering the remaining images and triangulating new feature points. Experiments showed that the proposed approach produced similar quality models as compared to Bundler and VisualSFM, while being more efficient. A hierarchical methodology with many novel techniques was proposed to systematically improve the performance of SfM reconstruction [
26]. The proposed methodology partitioned the scene into many small, highly overlapping image groups. The image groups were reconstructed individually, and then merged together to form a complete reconstruction of the scene. The proposed pipeline reduced the runtime on a large dataset by 36% when the overlap ratio between two image groups was set as 40%. A similar hierarchical approach was proposed for large-scale SfM [
27]. Images were firstly organized into a hierarchical tree using agglomerative clustering. Smaller image sets were reconstructed and merged in a bottom-up fashion. A scalable hierarchical SfM pipeline was proposed to process city-scale aerial images on a cluster of ten computers [
28]. Images were clustered by graph division and expansion. The image clusters were reconstructed in an incremental manner. The reconstructed clusters were merged using robust motion averaging. The hybrid pipeline performed well in terms of robustness and efficiency. A novel methodology was proposed to systematically improve the performance of hierarchical SfM for large-scale image sets [
29]. Images were clustered based on a dynamic adjustment strategy. Unreliable clusters were removed, and corresponding images were redistributed. Experiments on large terrestrial and aerial datasets demonstrated the robustness and efficiency of the pipeline. A hierarchical approach with a focus on cluster merging was proposed [
30]. Images were divided into non-overlapping clusters via an undirected weighted match graph. The match graph was simplified with a weighted connected dominating set, and a global model was extracted. After parallel reconstruction, clusters were merged based on the extracted global model.
In addition to the above research directions, reducing the scale of a reconstruction problem becomes a noteworthy line of research. It improves the efficiency of SfM by reducing the number of parameters to be optimized in a reconstruction. An efficient pipeline based on image clustering and the local iconic scene graph was proposed [
31]. Images were firstly clustered based on visual similarity. Then, local iconic scene graphs corresponding to city landmarks were extracted from the image clusters. The local iconic scene graphs were processed independently using an incremental approach. Experiments showed that the pipeline could reconstruct landmarks of a city based on millions of Internet images on a single workstation within a day. The preemptive matching strategy proposed in [
18] only used only a proportion of top-scale SIFT feature points for image matching. This strategy significantly speeded up image matching. Furthermore, the efficiency of SfM was also improved as the estimated number of tracks was reduced. A reduced bundle adjustment model was proposed for oblique aerial photogrammetry [
32]. The poses of oblique images were parameterized with the poses of nadir images and constant relative poses between oblique and nadir cameras. This approach significantly reduced the number of parameters and exhibited improvements in time and space efficiency. A track selection approach was proposed as a general technique for efficiency improvement [
33]. A subset of tracks was selected in consideration of compactness, accurateness, and connectedness. Experimental results demonstrated that the efficiency of two open-source SfM solutions was improved using the track selection approach. A method for selecting building facade texture images from oblique images based on existing building models was proposed for photorealistic building model reconstruction [
34]. Experimental results showed that the reconstruction process was significantly accelerated using the selected images. An oblique imagery selection methodology was proposed to improve the efficiency of SfM towards building reconstruction in rural areas [
35]. Oblique images covering buildings were automatically selected out of a large-scale aerial image set using Mask R-CNN. The selected oblique images and all nadir images were used for SfM reconstruction and dense matching. The approach improved the efficiency of SfM while obtaining dense clouds of similar quality compared to the conventional pipeline. A performant hierarchical approach based on track selection was proposed [
36]. The proposed approach firstly clustered the images based on their observation directions. Then, the tracks were selected based on a grid with a fixed spatial resolution. Submaps were sequentially reconstructed from the image clusters and merged. The hierarchical approach performed well on several large-scale datasets.
Although the above researches have made significant progresses in improving the efficiency of large-scale SfM, challenges still exist. In this paper, a hierarchical SfM pipeline based on an adaptive track selection approach is proposed for large-scale oblique images.
Section 2 details the workflow and procedures of the proposed methodology. Experimental results and comparisons with two widely used solutions are detailed in
Section 3. Discussions of the proposed methodology and the results are presented in
Section 4. Conclusions are made in
Section 5.
2. Methodology
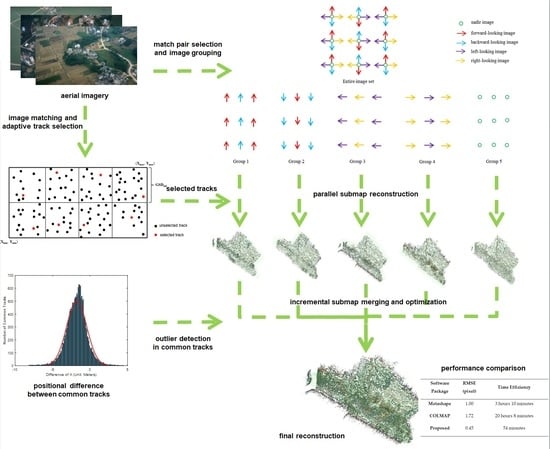
The workflow of the proposed methodology is illustrated in
Figure 1. Firstly, match pair selection is performed on an aerial image set using positioning and orientation (POS) data and the terrain of the survey area. Based on the match pair selection, pairwise image matching and image grouping are carried out. Adaptive track selection based on track georeferencing is performed after pairwise image matching to decimate tracks. The image grouping procedure divides the images to non-overlapping image groups. Based on the selected tracks, parallel reconstruction is performed on the image groups to generate submaps using incremental SfM in the object space. A novel method is proposed to detect the outliers in common tracks between the reconstructed submaps. Finally, the reconstructed submaps are incrementally merged.
2.1. Image Grouping Based on Traversal of Match Pairs
The image grouping procedure exploits match pairs and divides the entire image set to non-overlapping groups which do not have common images. Match pairs define the overlapping relationship between images which is usually used for pairwise image matching. The match pair selection method proposed in [
37] is used to generate match pairs in this study. The match pair selection process works as follows. Firstly, the principal point of each image is georeferenced using the acquired POS data and an existing elevation model of the survey area. Then, the overlapping relationship between images is determined based on the georeferenced principal points using the k-nearest neighbor search. In this study, seven match pairs are generated for each oblique image. These match pairs include two pairs from neighboring images acquired by the same camera, four pairs from neighboring images acquired by the camera looking at the opposite direction, and one pair from a neighboring nadir image. Four match pairs are generated for each nadir image. These match pairs include two pairs from neighboring nadir images in the same strip and two pairs from nadir images in the neighboring strips.
Based on the selected match pairs, the image grouping procedure divides the entire image set to five groups, as illustrated in
Figure 2. The entire image set is composed of images in three strips. There are three exposure positions in each strip. At each exposure position, images acquired by five cameras looking at different directions are exposed simultaneously. These images are represented by colored arrows and circles. The observation direction of an image is represented by the direction of an arrow. It can be seen from the figure that the image grouping procedure divides the images according to their spatial proximity and similarity of observation directions. Images in each group have similar observation directions, and each image spatially overlaps with its neighbors.
The algorithm for the image grouping procedure is described by Algorithm 1. When the procedure meets an unprocessed match pair, a stack is initiated, and the images from the current match pair are added to the stack. Then, the procedure pops an image from the stack at a time, and adds it to the current group. The procedure finds its match pairs in the entire set of match pairs. For each one in the found match pairs, the procedure adds the matched image to the stack if the match pair has not been processed. The current growing process terminates until the stack is empty. The image grouping procedure traverses all the match pairs and divides the images to five groups, as illustrated in
Figure 2.
| Algorithm 1 Image grouping by traversal of match pairs |
| Input: match pairs ; each pair specifies the match relationship between image i and j |
| Output: image groups |
| Initialization: |
| 1: for each pair in |
| 2: if is not processed |
| 3: initialize a new group |
| 4: initialize a stack , add and to |
| 5: while is not empty |
| 6: pop top element from , add to |
| 7: for each match pair in |
| 8: if is not processed |
| 9: push into |
| 10: end if |
| 11: end for |
| 12: end while |
| 13: add to |
| 14: end if |
| 15: end for |
| 16: return |
2.2. Adaptive Track Selection
Tracks correspond to 3D points in the object space. Tracks are generated from tie points which are determined by pairwise image matching. Pairwise image matching is carried out based on the result of the match pair selection. In this study, RootSIFT with the approximate nearest neighbor (ANN) algorithm is used to generate putative matches for each match pair. To speed up the matching process, the preemptive matching technique is used. Then, putative matches between two images are geometrically verified based on the fundamental matrix with RANSAC loops to generate tie points. Based on the geometrically verified tie points, the tracks are then generated.
To improve the efficiency of the following SfM reconstruction process, an adaptive track selection method is proposed. The adaptive track selection is performed on the generated tracks in the object space. The tracks are georeferenced to determine their positions in the object space, which is illustrated in
Figure 3. For a given track, its image observations are determined by pairwise matching. Therefore, its 3D position can be estimated using its image observations and the orientation observations of corresponding images.
In this study, the position of a track is calculated as follows. Firstly, the position is solved based on each observation using the DEM-aided georeferencing of a single image. Secondly, the georeferencing positions are averaged to determine the final position of the track. The fundamental model of DEM-aided direct georeferencing is the inverse form of the collinearity equations as follows.
where
is the spatial position of a track under the object coordinate system,
is the image observation of the track under the image plane coordinate system,
is the spatial position of the projection center under the object coordinate system, f is the focal length, and
to
are nine elements of the rotation matrix from the image space coordinate system to the object coordinate system.
The algorithm for the adaptive track selection procedure is described by Algorithm 2.
Basically, the procedure iteratively selects tracks until each image has no less than a minimum number of observations (MNO). To effectively decimate the tracks, the tracks with a large number of observations are preferable as they add more constraints. To select the tracks with a large number of observations, the track selection is conducted based on a series of 2D grids. Firstly, the range of the grids is determined based on the result of track georeferencing. Then, an initial ground sample distance (
) is calculated, and a grid is initialized. The tracks are mapped to the cells of the grid based on their 2D position. Then, the track with the maximum number of observations is selected from each cell of the grid. To guarantee that all the images reach the MNO, the track selection works in an iterative manner. In each iteration, the
is halved and a new grid is generated with finer cells. The remaining tracks are mapped to cells of the new grid. The track with the maximum number of observations is selected from each cell.
| Algorithm 2 Adaptive track selection |
| Input: tracks , where each track stores its image observations; the value of ; the number of observations operator |
| Output: selected tracks |
| Initilization: |
| 1: for each track in |
| 2: georeference |
| 3: end for |
| 4: calculate |
| 5: initialize a set |
| 6: add all the images into |
| 7: initialize the ground sample distance |
| 8: while is not empty |
| 9: initialize 2D grid with |
| 10: for each track in |
| 11: if is in |
| 12: continue |
| 13: end if |
| 14: find the images to which is visible |
| 15: if |
| 16: continue |
| 17: end if |
| 18: find the cell in which lies |
| 19: if is occupied by another track and |
| 20: continue |
| 21: else |
| 22: stores in |
| 23: end if |
| 24: end for |
| 25: for each cell in grid |
| 26: add the track stored in to |
| 27: end for |
| 28: update according to |
| 29:
|
| 30: end while |
| 31: return |
The initial
of the grid
is calculated according to Equation (3).
where
and
are the width and height of the ground projection of an image, respectively. The first two iterations of the track selection process are illustrated in
Figure 4.
Figure 4a shows the initialized grid with the initial
. The points in the figure are the tracks mapped to the cells. The red point in each cell indicates the selected track with the maximum number of observations.
Figure 4b shows the result of the second iteration. The
is halved and the tracks with the maximum number of observations in the cells are selected.
2.3. Parallel Submap Reconstruction and Incremental Submap Merging
Based on the selected tracks, submaps are reconstructed from image groups in parallel. Each submap is reconstructed using incremental SfM in the object space. The optimization problem is formulated as a joint minimization of the sum of the squared reprojection errors and the sum of the squared positioning errors. The object function for the optimization is given by Equation (4).
where
is an image observation of a 3D point
on image
j,
represents the camera parameters of image
j,
is the function that projects a 3D point onto the image plane,
denotes the L2-norm,
is the position observation of image
k,
is the estimated position of image
k,
is an indicator function with
= 1 if point
is visible to image
(otherwise,
= 0).
is a weight for the squared positioning errors, and it is calculated according to Equation (5).
where
is the accuracy of image observations, while
is the accuracy of the global navigation satellite system (GNSS) observations.
Common tracks between two submaps can be determined with ease as all submaps are reconstructed based on the same set of selected tracks. To detect the outliers in the common tracks between two submaps, the positional difference in common tracks is exploited. It can be assumed that
and
are estimated coordinates of two common tracks with the same index
i.
is taken from Submap 1 and
is taken from Submap 2. It can be assumed that:
where
is the true coordinate of the track,
and
are the residual errors corresponding to
and
, respectively. It can be assumed that
and
are subject to two normal distributions, as follows.
where
and
are the means of the distributions, while
and
are the variances in the distributions. The positional difference
between
and
is given by Equation (10).
Based on the above assumptions, it can be deduced that
is subject to the normal distribution given by Equation (11).
Based on the normal distribution of , the three-sigma rule is used to detect and remove outliers in the common tracks. Specifically, a pair of common tracks is determined as an outlier as long as the positional difference along an axe is outside the range of the corresponding mean value plus and minus three times the corresponding standard deviation.
After the detected outliers are removed from the common tracks, the submaps are incrementally merged. The submap reconstructed from the image group composed of nadir images is used as the base map. The other submaps are incrementally merged to the base map. To merge a submap, a similarity transformation is firstly estimated. For common tracks {
} and {
}, the transformation can be estimated by minimizing the object function given by Equation (12).
where
is the rotation matrix,
is the translation vector,
is the scaling factor, and
is the Huber loss function.
denotes the L2-norm.
Then, the estimated transformation is applied to the submap. The transformed submap is locally optimized with common tracks fixed to their counterparts in the base map. After merging the submap and the base map, the merged map is globally optimized and used as the base map for merging the next submap. For the local and global optimization, the problem for refining camera poses and 3D tracks is formulated to minimize the first term of Equation (4), where the sum of squared errors between the tie point observations and projections of the corresponding tracks is minimized.
4. Discussion
The proposed image grouping method is based on match pair selection and requires precision in the selected match pairs. The used match pair selection method generated match pairs using the position of images, the observation directions of images, and the terrain of the survey area. The pair-wise image matching results show that the generated match pairs are precise. The proposed image grouping method exploits the structure underlying an aerial survey which is generally based on regularly distributed exposures located in the parallel strips. The regularity of exposure also guarantees that images are acquired by two oblique cameras with opposite observation directions that overlap well with each other. The grouping procedure divides the images to non-overlapping groups instead of overlapping groups. This strategy avoids setting the overlapping ratio parameter which defines the ratio of images that two overlapping groups have in common. If the overlapping ratio parameter is set too high, the size of the generated image groups will increase. The efficiency of the submap reconstruction and merging will decrease. If the ratio parameter is set too low, the common images must lie at the boundary of the image groups. Then, the robustness and the accuracy of the submap reconstruction and merging will probably decrease as the estimated orientations of images at the boundary of an image network are generally of low accuracy.
The proposed method iteratively selects tracks using a series of 2D grids. The proposed method uses a series of grids instead of a single grid with a constant GSD for several reasons. Experimental results have shown that the density of tracks is highly correlated with the land cover of the survey area. It can be expected that the number of observations of an image acquired over a building-covered area is larger than that of an image acquired over a farm field. If a grid with a large GSD is used for track selection, images acquired over a farm field may fail in registration due to the lack of sufficient observations. If a grid with a small GSD is used, the efficiency of reconstruction will decrease as a large number of tracks are selected. On the contrary, the proposed method iteratively selects tracks until all images reach the MNO threshold. The MNO threshold is more meaningful than a constant GSD for image registration as the robustness of registration generally depends on the number of observations. Moreover, the iteratively halved GSD makes the track selection process converge fast as the number of selected tracks theoretically quadruples in each iteration. Therefore, the proposed iterative track selection method is effective and efficient.
As the selected tracks are used by the reconstruction of submaps, common tracks between the reconstructed submaps can be determined without difficulty. To detect outliers in the common tracks, the three-sigma rule is performed based on the positional difference in the common tracks. The proposed outlier detection method insists that the submaps are reconstructed in the object space. The experiments show that the proposed outlier detection model fits well with the data. The detected outliers show that the classical robust image matching technique cannot remove all the outliers from the matches. Image matching techniques taking into account relationship among feature points could be used to solve this problem.
Five submaps were reconstructed in parallel from corresponding image groups. The experimental results show the high performance of the parallel reconstruction. Although the image groups could be further divided to smaller ones, the time efficiency of the submap reconstruction might not be further improved as CPU usage had already approached 100% during the experiments. The nadir submap reconstructed from the nadir images was the only submap that had common tracks with the other four submaps. Moreover,
Figure 6 shows that the mean track length and mean image observations of the nadir submap were larger than those of the oblique submaps, which indicates that the image network of the nadir submap was more stable than that of the oblique submaps. Therefore, the nadir submap was used as the base map during the submap merging process in favor for its stable network and high connectivity. The accuracy of the final map reflects the high inner consistency of the proposed submap merging method. However, the proposed submap merging method was suboptimal as the oblique submaps were optimized with common tracks fixed to their positions in the nadir submap. The absolute positioning accuracy of the final map will be systematically investigated in future work.