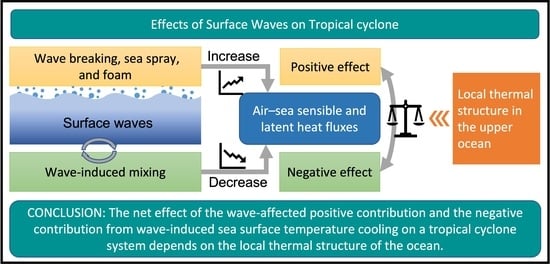
Effects of Surface Wave-Induced Mixing and Wave-Affected Exchange Coefficients on Tropical Cyclones

Abstract

Surface waves perform a crucial role in modulating tropical cyclone (TC) systems and have proved to be key for numerical TC predictions. In this study, we investigate the effects of wave-induced mixing and wave-affected surface exchange coefficients using a coupled ocean–atmosphere–wave model for two real TC cases: Shanshan (2018) and Megi (2010). The results demonstrate that wave-affected surface exchange coefficients enhance air–sea heat fluxes and have a significantly positive effect on simulated TC intensity, size, and strengthening process. In contrast, the wave-induced mixing has a negative impact on TC intensity and size and is not conducive to TC intensification and maintenance. The net effect of these two factors is a balance between the wave-affected positive contribution and the negative contribution from wave-induced sea surface temperature cooling. We find that the effect of wave-induced mixing on a TC system depends on the local thermal structure of the ocean. When the thermocline is weak and there is warm water at the wave-induced mixing penetration depth, the negative effect of the wave-induced mixing is weak. However, when there is cold subsurface water and a strong thermocline, wave-induced mixing has a significant impact, which exceeds the wave-driven positive feedback.

1. Introduction

A tropical cyclone (TC) is a powerful atmospheric vortex that can damage human life and industry, so the importance of TC prediction has long been recognized. Over recent decades, significant progress has been made in forecasting TC tracks [1,2]. Between 1990 and 2020, track-forecast errors have reduced by around 60% for forecast periods of 24–120 h, according to National Hurricane Center official forecast error database (https://www.nhc.noaa.gov/verification/verify7.shtml, accessed on 1 July 2022). However, improvements of TC intensity forecast remain limited [1,2,3]. The accuracy of TC intensity forecasts improved 2–20% for forecast periods of 24–120 h between 1990 and 2020 (https://www.nhc.noaa.gov/verification/verify7.shtml, accessed on 1 July 2022). The forecast accuracy for TC size (usually defined as wind radii for a specific wind speed, e.g., 34 kt, 50 kt, or 64 kt) remains uncertain, despite many studies investigating uncertainty and proposing improved methods of estimating TC size [4,5,6,7].

A TC is a complex phenomenon of air–sea–wave interactions, and gains energy from the warm upper ocean to develop and mature. The strong winds associated with a TC generate ocean surface waves and drive ocean circulation, which is accompanied by Ekman pumping. These strong winds, surface waves, and local ocean circulation patterns enhance mixing in the upper ocean and entrain cold water below the thermocline. This reduces sea surface temperature (SST), which markedly impacts ocean–air heat transfer, thus weakening the TC [8,9,10,11]. Wave-induced mixing performs an important role in modulating the upper ocean mixing layer under a TC [10,12,13,14,15]. Complicated small-scale processes, such as wave breaking, sea spray, and foam bubbles, occur at the sea surface under high wind conditions. These small-scale processes affect air–sea interactions under TC conditions, significantly affecting surface exchange coefficients and promoting TC intensification [16,17,18,19].

The physical processes associated with waves at the air–sea interface are not well represented in current numerical models and improvements are needed. For example, ocean models generally do not explicitly include the wave-induced mixing that is attributable to wave breaking, wave orbital motion, or Langmuir circulation [20,21,22], and this results in overestimates for SST in summer [22,23,24]. The surface exchange coefficients in atmosphere models (e.g., the drag and enthalpy exchange coefficients) have high uncertainty at high wind speeds due to our limited understanding of the wave-related microphysics of air–sea interactions, such as wave breaking, sea spray, and foam. This lack of understanding stems largely from the difficulties associated with obtaining observations of an extreme sea state [16,17,25]. The incomplete representation of these processes in numerical models, especially in coupled models, limits the accuracies of TC intensity and size prediction [10,11,26,27].

This paper aims to investigate the effects of wave-induced mixing and wave-affected surface exchange coefficients on TCs by hindcasting two TCs with different natures using a coupled ocean–atmosphere–wave model. Our goals are as follows:

(1)

Investigate how wave-induced mixing and wave-affected surface exchange coefficients affect the track, intensity and size of a TC, and analyze air–sea interactions.

(2)

Study the combined effects of wave-induced mixing and wave-affected surface exchange coefficients on TCs, including how the impacts of these two factors differ.

The remainder of this paper is organized as follows: Section 2 describes theoretical wave-related processes (including wave-induced mixing and small-scale wave-related processes at the air–sea interface) and their effects on TC systems. Section 3 briefly describes the coupled ocean–atmosphere–wave model and details the experiment setup. Section 4 presents the results for two TC cases. Section 5 presents a summary and conclusions.

2. Background

2.1. Wave-Induced Mixing

It is known that surface waves contribute to mixing in the upper ocean [20,21,22,28,29,30]. Wave breaking can generate turbulence and directly facilitate mixing down to a depth of the order of the wave height [31,32]. In general, wave breaking has only a small effect on SST unless the thermocline is very shallow [33,34,35]. Zhang W. et al. [10] investigated the effect of wave-breaking induced mixing on Typhoon Megi (2010) and found that it had quite a small impact on the typhoon intensity and size because the mixing due to wave breaking is limited to the shallow depth near to the surface, which has a minor effect on SST and heat fluxes under relatively deep mixed layer conditions.

Wave orbital motion can also produce turbulence and enhance mixing down to a depth of the order of the wavelength [20,22,36]. Numerical studies have concluded that including wave orbital motion in ocean models can significantly improve predictions of SST and mixed layer depth (MLD) and produce results that are in good agreement with observed physics, such as the thermal structure and profiles of suspended sediment in the upper ocean [10,14,22,36,37]. Recent studies have indicated that wave-orbital-motion induced mixing has a negative effect on TC intensity and size [10,11].

Another mechanism through which surface waves enhance mixing in the upper ocean is Langmuir circulation [21,29,38]. Previous studies have indicated that explicitly implementing Langmuir circulation in ocean models reproduces ocean response to TC conditions well [13,15]. However, there remain large differences among different parameterization schemes for Langmuir circulation, making it difficult to investigate and understand its effects [39].

According to previous studies, it is still an open question that whether the wave-related mixing mechanisms between wave orbital motion and Langmuir circulation are completely different or whether an overlap exists between these two processes, because both of them are directly related to the water particle orbits. The theory of wave orbital motion induced mixing seeks to explain the enhanced turbulence due to the localized shear flow (induced by wave orbits) that transfers energy into turbulence through the way of stretching vortex line [40]. Langmuir circulation or turbulence theory focuses on the effect of Stokes drift interacting with wind induced vorticities, which leads to entrainment and enhanced mixing [21,29]. In this aspect, they seem to be different, but they both involve the interaction between surface waves and other motions. Pragmatically, the difference between these two theories is whether the turbulent mixing changes more directly in response to Stokes drift characteristics or wave orbital velocity statistics. However, it is a challenge to distinguish them clearly, because they are co-vary. Numerical studies show that each of these two wave-related mixing mechanisms can significantly increasing the mixing in the upper ocean when they are considered separately in the ocean model [12,13,14,15,36], whereas the parameterization process of these two factors together can be complicated, and there is no reliable parameterization scheme combining these two mechanisms together at present because they are not always distinguishable by comparison with data. In this paper, we temporarily consider wave orbital motion induced mixing to investigate the effect of wave-induced mixing on the TC system, and do not include Langmuir circulation which has various parameterization schemes. We also neglect wave-breaking induced mixing. Zhang W. et al. [10] demonstrated that wave orbital motion performs a greater role in modulating the TC system than does wave breaking, and that the effect of wave breaking is negligible compared with the effect of wave-orbital-motion induced mixing.

Ghantous and Babanin [41] described the turbulence that is driven by wave orbital motion as:

$$P=bk{\omega }_p^3\frac{H_S^3}{8}{e}^{3kz},$$

(1)

where b is a dimensionless proportionality coefficient, k is peak wave number, ω_p is the peak radian frequency, Hs is the significant wave height, and z is the water depth (positive upward). In this paper, b is set to 0.0014, which has been shown to achieve reasonable results that are close to observed values [10,12,42]. P can be included in a two-equation turbulence closure scheme, such as the General Length Scale scheme (GLS) [43]:

$$\frac{D}{Dt}\left(K\right)=\frac{\partial }{\partial z}\left[\frac{{\nu }_t}{{\sigma }_k}\frac{\partial }{\partial z}\left(K\right)\right]+P_s+P+P_b-\epsilon {,}_{ }$$

(2)

$$\frac{D\psi }{Dt}=\frac{\partial }{\partial z}\left(\frac{{\nu }_t}{{\sigma }_{\psi }}\frac{\partial \psi }{\partial z}\right)+\frac{\psi }{K}\left(c_1\left(P_s+P\right)+c_3{P}_b-c_2\epsilon F_{wall}\right),$$

(3)

where K is the turbulent kinetic energy, and $\psi$ is a generic parameter used to describe the turbulence length scale. The first terms on the right hand sides of Equations (2) and (3) are the turbulent transport terms for K and $\psi$, respectively; $P_s$ and $P_b$ are the shear and buoyancy production, respectively; ε is the dissipation rate of K; $F_{wall}$ is a wall function; $c_1$, $c_2$, and $c_3$ are constants; ${\nu }_t$ is the eddy viscosity for momentum; and ${\sigma }_k$ and ${\sigma }_{\psi }$ are the turbulent Schmidt numbers for K and $\psi$, respectively.

In our study, we have implemented Equation (1) in the code for the ocean model to represent wave-orbital-motion induced mixing (hereafter wave-induced mixing for brevity). The ocean model is described in Section 3.2. Further details of the GLS mixing scheme have been provided by Umlauf and Burchard [43] and Warner et al. [44].

2.2. Wave-Related Small-Scale Processes in the Air–Sea Boundary Layer

Waves at the sea surface undergo complex changes under high wind conditions, including wave breaking and the generation of a large number of sea spray droplets and bubbles. These small-scale wave-related processes can lead to reduction or saturation of the drag coefficient ($C_D$), which directly affects air–sea momentum fluxes and impacts TC intensity [16,19,45,46,47]. When sea-spray droplets are injected into the atmosphere, they are accelerated by the wind and gain horizontal momentum. When they fall back to the sea surface, the droplets transfer their horizontal momentum to the ocean. Droplet evaporation processes change the turbulent kinetic energy and buoyancy generation in the air–sea boundary layer, thus changing the stability of the boundary layer. Rastigejev et al. [46] pointed out that the above two processes can reduce the drag coefficient. At the same time, wave breaking leads to changes in the flow characteristics of air blowing over the wave crest, which inhibits steepening of the wave and may reduce or saturate the drag coefficient [16,48,49]. In addition, the presence of foam at high wind speed makes the sea surface smoother and reduces the drag coefficient [19]. In terms of summarizing observations, some measurements have suggested that C_D tends to decrease at high wind speeds [50,51,52], other field and laboratory studies show that C_D becomes level-off [16,53,54,55]. In our present work, we chose a C_D with a saturated trend at high wind speed (details are below), and the examining of a C_D with a decreased trend will be complete in the next work.

Sea spray performs an important role in mediating enthalpy fluxes under TC conditions [9,18,56,57]. When a droplet enters the atmosphere, there is a sensible heat transfer between the droplet and the atmosphere, then evaporation occurs and releases water vapor [49,58]. Evaporation of sea spray droplets can sharply cool the air near the sea surface, thus increasing the interfacial sensible heat flux [59]. Richter and Stern [17] estimated surface enthalpy fluxes obtained from dropsonde data and concluded that ocean–atmosphere enthalpy exchange is likely to be dominated by sea spray when a TC is present.

The enthalpy exchange coefficient ($C_K$), or of wave-mediated heat fluxes, remain highly uncertain owing to the difficulties of obtaining reliable observations under TC conditions [16,18,60]. By convention, $C_K$ is extrapolated from measurements made at wind speeds of less than 30 m/s for high wind conditions [16]. In the classic and widely used Coupled Ocean–Atmosphere Response Experiment (COARE) algorithm, $C_K$ grows weakly with increasing wind speed [61]. Several studies have indicated that $C_K$ does not depend significantly on wind speed at extremely high wind speeds [17,53]. However, these results are inconclusive, as there are large relative errors or uncertainties in the measurements that have been used, and in SST values that have been obtained using indirect methods [16,17]. Recent laboratory results from Komori et al. [16] and Troitskaya et al. [54] show that $C_K$ increases sharply at wind speeds exceeding 33–35 m/s. Komori et al. [16] suggested that this sharp increase in $C_K$ is caused by wave breaking and sea spray. Troitskaya et al. [60] hypothesized that this phenomenon may be associated with increased whitecapping.

At high wind speeds, the surface exchange coefficients, $C_D$ and $C_K$, are dominated by wave-related small-scale processes, as discussed earlier. We refer to these coefficients as wave-affected surface exchange coefficients. The values for $C_D$ and $C_K$ that are proposed by Komori et al. [16] were measured under 10 m wind speeds ranging from 7.3 m/s to 67 m/s in a high-speed wind–wave tank and are expressed as:

$$C_D=\{\begin{array}{cc}1.0\times {10}^{-3}\hfill & \hfill U_{10}<5.2 \mathrm{m}/\mathrm{s}\\ 4.4\times {10}^{-4}{U}_{10}^{0.5}\hfill & \hfill 5.2\le U_{10}<33.6 \mathrm{m}/\mathrm{s},\\ 2.55\times {10}^{-3}\hfill & \hfill U_{10}\ge 33.6 \mathrm{m}/\mathrm{s}\end{array}$$

(4)

$$C_K=\{\begin{array}{cc}1.39\times {10}^{-3}\hfill & \hfill U_{10}<33.6 \mathrm{m}/\mathrm{s}\\ 6.51\times {10}^{-5}{U}_{10}-7.99\times {10}^{-4}\hfill & \hfill U_{10}\ge 33.6 \mathrm{m}/\mathrm{s}\end{array}.$$

(5)

These two formulations for $C_D$ and $C_K$ implicitly include wave-related small-scale processes, such as wave breaking, sea spray, and foam. In this paper, we use Equations (4) and (5) to define wave-affected exchange coefficients and to calculate air–sea momentum and heat fluxes using the following bulk algorithm:

$$\tau ={\rho }_a{C}_D{U}_{10}^2,$$

(6)

$$Q_L=-{\rho }_a{L}_v{C}_L{U}_{10}\left(q_{10}-q_s\right),$$

(7)

$$Q_S=-{\rho }_a{C}_p{C}_S{U}_{10}\left({\theta }_{10}-{\theta }_s\right),$$

(8)

where $\tau$, $Q_L$, and $Q_S$ are the momentum, latent heat, and sensible heat fluxes, respectively; ${\rho }_a$ is air density; $L_v$ is the latent heat of vaporization; $C_p$ is the specific heat capacity of humid air; $C_D$, $C_L$, and $C_S$ are the surface exchange coefficients at 10 m height for drag (momentum), latent heat, and sensible heat, respectively; $U_{10}$ is the 10 m wind speed above the sea level; q is the specific humidity; and $\theta$ is temperature. Subscripts “10” and “s” indicate reference heights of 10 m and the sea surface, respectively. Komori et al. [16] verified the conventional assumption that $C_K$ = $C_L$ = $C_S$. Figure 1 shows the curves for $C_D$ and $C_K$ from COARE 3.0 (for details, see the Appendix A) and Komori et al. [16].

In some studies into the effect of sea spray on TCs, spray-mediated heat fluxes are added to interfacial heat fluxes, which are generally estimated using a value for $C_K$ that is extrapolated from measurements made at low and moderate wind speeds, following convention [9,11,62,63,64]. In this case, the spray-mediated heat fluxes depend on the sea spray generation function (SSGF). However, the SSGF is uncertain because of the difficulties of recording observations under the severe conditions of TCs, meaning that the appropriate form for the SSGF remains controversial [57]. Different SSGFs predict droplet amounts that vary by more than six orders of magnitude, assuming a consistent droplet size and wind speed [57,65]. Recently, Sroka and Emanual [18] suggested that calculation of spray-mediated flux can be represented more simply as a function of sea spray volume, making the calculated flux insensitive to the shape of the SSGF. However, different SSGFs result in vastly different sea spray volume flux estimates [18], thus leading to large uncertainties in calculations of the heat flux under sea spray conditions.

3. Materials and Methods

3.1. Experiment Design

In this study, we chose two real TC cases with different intensities to evaluate the impacts of wave-related small-scale processes and wave-induced mixing on TCs. The first case is Typhoon Shanshan (2018), which had a relatively weak intensity, with peak maximum sustained winds of around 36 m/s, according to the Japan Meteorological Agency (JMA). Shanshan originated as a tropical depression in the western North Pacific at 08:00 UTC on 3 August 2018, then moved north-northwestward and strengthened gradually (Figure 2). Shanshan was upgraded to typhoon grade (maximum sustained winds of ≥32 m/s) on 4 August and maintained maximum sustained winds near 36 m/s for the next five days. Shanshan’s center made a close approach to Japan’s eastern coast and travelled roughly parallel to the Japanese coasts of Chiba and Ibaraki prefectures on 8 and 9 August. On the morning of 9 August, Shanshan made a sharp turn to the east-northeast and accelerated into the open waters of the North Pacific, where its intensity began to weaken. Finally, Shanshan ceased to be numbered at 14:00 UTC on 10 August 2018.

The second case is Super Typhoon Megi (2010), which was the strongest tropical cyclone recorded in 2010, with maximum sustained winds up to 65 m/s at its peak intensity, according to JMA. Megi began in the western North Pacific at 00:00 UTC on 13 October 2010, then moved northwest and strengthened gradually (Figure 3). After 12:00 UTC on 16 October, Megi moved gradually west-southwestward and continued to strengthen, then made landfall in the northeastern Philippines at 04:25 UTC on 18 October. After passing through the Philippines, Megi entered the South China Sea and turned sharply to the north at 00:00 UTC on 20 October, lingering in the South China Sea for five days. Finally, Megi made its second landfall on the southern coast of Fujian in China at 04:55 UTC on 23 October.

We conducted four numerical experiments for each TC case to investigate the effects of surface waves (including wave-induced mixing and wave-affected momentum, and enthalpy exchange coefficients) on the TC system. Experiment R0 was the control run, in which we used the classical COARE 3.0 algorithm to calculate surface exchange coefficients (see details in the Appendix A) and excluded the effect of wave-induced mixing. In experiment R1, we implemented the leveled-off drag coefficient from Equation (4) and the high enthalpy exchange coefficient from Equation (5) at high wind speeds. In experiment R2, we used Equation (1) to consider the effect of wave-induced mixing. Finally, the effects of the wave-affected surface exchange coefficients and wave-induced mixing were taken into account in experiment R3.

Table 1. Numerical experiment design.

Expts.	Parameterizations for the Surface Exchange Coefficients	Wave-Induced Mixing
R0	COARE 3.0	No
R1	Equations (4) and (5)	No
R2	COARE 3.0	Equation (1)
R3	Equations (4) and (5)	Equation (1)

presents a summary of the experiments.

3.2. Model Description and Set up

We use the coupled ocean–atmosphere–wave–sediment transport model COAWST [66] to investigate the effects of wave-affected surface exchange coefficients and wave-induced mixing on the two TC systems. COAWST includes atmosphere, ocean, wave, and sediment components, i.e., the Advanced Research Weather Research and Forecasting model (ARW–WRF, hereafter WRF) [67], the Regional Ocean Modeling System (ROMS; http://www.myroms.org, accessed on 2 June 2022), the Simulating Waves Nearshore model (SWAN) [68], and the USGS Community Sediment Model [69], respectively. The latest version of COAWST also includes a hydrology component—Hydrologic Rainfall-Runoff Model (WRF-Hydro, https://ral.ucar.edu/projects/wrf_hydro/overview, accessed on 2 June 2022), a state-of-the-art spectral wave modeling system—WAVEWATCH III [70], and an infragravity wave driver—Infragravity wave model (InWave). The three components of COAWST used in our numerical experiments (WRF, ROMS, and SWAN) are described briefly below. A full description of COAWST has been provided by Warner et al. [66] and in https://www.usgs.gov/centers/whcmsc/science/coawst-coupled-ocean-atmosphere-wave-sediment-transport-modeling-system#overview (accessed on 2 July 2022).

WRF is a flexible, state-of-the-art atmosphere simulation system that serves a broad range of meteorological applications across scales from tens of meters to thousands of kilometers. It provides a variety of schemes for the representation of different physical processes, such as microphysics, surface layers, and longwave and shortwave radiation schemes. In our numerical experiments, we used the Nakanishi and Niino surface layer scheme [71], the Rapid Radiative Transfer Model longwave radiation scheme [72], the Dudhia shortwave radiation scheme [73], the Lin microphysics scheme [74], and the Noah land surface scheme [75].

ROMS is a three-dimensional (3D), free surface, terrain-following numerical model that is appropriate for (and widely used in) a diverse range of applications including the current system, astronomical tide movement, ecosystem, and sea ice. In ROMS, transport equations are utilized to solve momentum, scalar advection, and diffusion processes, and an equation of state—accounting for temperature, salinity, and suspended-sediment contributions—is used to compute the density field. In our study, we utilize the Chapman and Flather conditions for the free surface and two-dimensional momentum, respectively, and we use the radiation boundary condition with nudging for 3D momentum. We use the third-order upstream horizontal advection scheme, the fourth-order centered vertical advection scheme, and the harmonic horizontal diffusion scheme for momentum, temperature, and salinity in our experiments, and we adopt the GLS vertical mixing scheme for mixing [43].

SWAN is a third-generation wave model and can be used for coastal regions and inland waters. It accounts for various wave related physics, including wave propagation in time and space, shoaling, refraction owing to current and depth, frequency shifting owing to current and non-stationary depth, wind-driven wave generation, three- and four-wave interactions, whitecapping, bottom friction and depth-induced breaking, dissipation, wave-induced set-up, transmission through and reflection against obstacles, and diffraction.

The Model Coupling Toolkit is used in COAWST to exchange data between the three sub-model components. When WRF is coupled to ROMS, the momentum and heat fluxes calculated by WRF are transferred to ROMS using a flux-conservative remapping scheme which ensures consistent momentum and heat fluxes between WRF and ROMS, and the sea surface temperature is passed from ROMS to WRF for estimation of air–sea heat fluxes. In WRF–SWAN coupling, WRF estimates of 10 m winds are used to drive SWAN, and COAWST provides three options to allow exchange of wave data (significant wave height, wavelength, and wave period) to WRF for calculating the surface roughness through consideration of wave–atmosphere interactions [76]. If none of these three options is selected, the COARE 3.0 will be active. In our study, we conducted the experiment R0 as the control run by activating the COARE 3.0 algorithm, then modified the code (in experiments R1 and R3) to estimate air–sea fluxes using Equations (4) and (5), which implicitly include the effects of wave-related small-scale processes, such as wave breaking, sea spray, and foam. The coupling between ROMS and SWAN allows the impacts of surface waves on ocean circulation to be taken into account in ROMS [77]. Wave-related parameters, such as significant wave height, wavelength, wave direction, wave period (surface and bottom), percentage wave breaking, wave energy dissipation, and bottom orbital velocity, are passed from SWAN to ROMS. Currents and sea surface elevations are passed from ROMS to SWAN for modulation of the wave fields. Note that the C_D scheme in SWAN has not been adjusted to be consistent with WRF in COAWST. We followed the default setting for C_D to avoid some potential risks or conflicts that crash the wave model. In the wave model, there are various empirical parameters, and many of them have been tuned based on the C_D. When the C_D is changed in SWAN, the balance between the original wind input and the wave breaking dissipation could be broken. Therefore, a more rigorous way to do this is to change the C_D, then recalibrate all the empirical parameters of the model again (e.g., parameters of the wave breaking term), but this is another research topic, which is beyond the scope of our present paper. In terms of the consistency between sub-model components, more work on the coupling model is required.

For Typhoon Shanshan, the simulation period was from 00:00 UTC 4 August to 00:00 UTC 8 August 2018, and the modeled domain was 15°N–36°N, 137°E–154°E. For Super Typhoon Megi, the simulation period was from 00:00 UTC 15 October to 18:00 UTC 17 October 2010, and the modeled domain was 10°N–24°N, 118°E–141°E. ROMS was initialized from a hot start following the solutions provided by previous simulation works that simulated TCs using COAWST [66,78,79]. The outputs of Hybrid Coordinate Ocean Model with the Navy Coupled Ocean Data Assimilation (NCODA) system (hereafter HYCOM GLBa0.08; see details in Section 3.3), such as 3-D velocity, temperature, salinity, and sea surface elevation, were used to derive the initial and boundary conditions for ROMS. This data quality is sufficient for our simulation of several days. Additionally, the Orlanski-type radiation condition was used together with relaxation to downscale daily salinity and temperature tracer, and 3-D velocity of HYCOM GLBa0.08. Boundary conditions of the free-surface and depth-averaged velocity were solved using Flather scheme with HYCOM GLBa0.08 data. The spin up periods for WRF and SWAN were both 24 h, so the results of the first day of the simulation periods were not considered in the validation part. WRF started with data from the National Centers for Environmental Prediction (NCEP) Final Operational Global Analysis (FNL) dataset and the initial field was also adjusted by the JMA best track data through the use of a vortex scheme embedded in WRF. SWAN was initialized using the stationary mode to obtain a steady state. A uniform grid spacing of 6 km is used for both typhoon cases, and the same horizontal grids are used for ROMS, WRF, and SWAN (273 × 381 horizontal grids for Shanshan and 424 × 256 horizontal grids for Megi). ROMS contains 30 vertical levels, described by the stretched terrain-following coordinate, with higher vertical resolution in the upper mixing layer; WRF uses 31 sigma levels. SWAN resolves 24 wave frequencies (logarithmically spaced from 0.04 to 1.0 Hz) and 36 wave direction bands, each 10° wide. The time steps for ROMS, WRF, and SWAN are 30 s, 30 s, and 60 s, respectively. The three model components exchange data every 10 min.

3.3. Data Description

The initial and lateral boundary conditions for WRF (e.g., air temperature, pressure, winds, and humidity) were taken from the National Centers for Environmental Prediction (NCEP) Final Operational Global Analysis (FNL) dataset (https://rda.ucar.edu/datasets/ds083.2, accessed on 2 June 2022), with spatial and temporal resolutions of 1° and 6 h, respectively. The initial and boundary conditions of ocean temperature, salinity, current, and sea surface elevation for ROMS were obtained from the HYCOM GLABa0.08 dataset (https://www.hycom.org/dataserver, accessed on 2 June 2022), which has a spatial resolution of 1/12° and is assimilated with available SST from satellite, and available vertical temperature and salinity profiles from XBTs, ARGO floats, and moored buoys. The boundary conditions for SWAN were taken as JONSWAP spectra [80].

The best track data for Shanshan and Megi from the JMA (https://www.jma.go.jp/jma/jma-eng/jma-center/rsmc-hp-pub-eg/trackarchives.html, accessed on 2 June 2022) were used to verify our simulation results. This dataset covers tropical cyclones that have developed over the western North Pacific since 1951. The present version of the dataset includes 6-hourly tracking, intensity, and size analyses. The daily microwave-only (MWO) SST products from the Remote Sensing System (RSS; https://www.remss.com/measurements/sea-surface-temperature/, accessed on 2 June 2022) were used to assess the modeled sea surface temperature output from the ocean model. The wind data from the Advanced Scatterometer (ASCAT) onboard the EUMETSAT MetOp-A platform (https://www.remss.com/missions/ascat/, accessed on 2 June 2022) and the WindSat radiometer onboard the Coriolis satellite (https://www.remss.com/missions/windsat/, accessed on 2 June 2022) were used to validate our simulated TC size. Significant wave heights and wind speeds derived from six altimeters—Jason-1, -2, -3, Sentinel, Cryosat, and Envisat (sourced from Australia’s Integrated Marine Observing System)—were used to assess our modeled wave heights and wind speeds (http://portal.aodn.org.au/search, accessed on 2 June 2022) [81].

4. Results

4.1. TC Track, Intensity, and Size

4.1.1. TC Track

Figure 2a and Figure 3a present the simulated and best tracks for Shanshan and Megi, respectively. These show that the modeled tracks generally match the best tracks well. For Shanshan, the simulated tracks for experiments R1 and R3, which consider the wave-affected surface exchange coefficients, have large errors, relative to experiments R0 (the control run) and R2 (which only includes wave-induced mixing). For Megi, the track errors in experiments R1 and R3 are smaller than those in experiments R0 and R2. The track errors are listed in detail in

Table 2. Statistics for the track, maximum wind speed at 10 m, minimum sea surface pressure (SSP), and longest radius of 30 kt winds, comparing modeled and best track data. See Section 3.1 for details of the different experiments.

Shanshan
Expt.	Track	Min SSP		Max Winds at 10 m		Longest Radius of 30 kt
	Error (km)	Error (hPa)	Relative Error (%)	Error (m/s)	Relative Error (%)	Error (km)	Relative Error (%)
R0	52.7	−6.7	0.75	0.6	4.5	−49.1	8.8
R1	111.0	−16.2	1.67	6.8	19.0	−5.8	3.4
R2	47.7	0.2	0.45	−3.1	8.7	−103.2	18.6
R3	91.6	−4.2	0.64	−0.8	5.2	−90.2	16.2
Megi
Expt.	Track	Min SSP		Max Winds at 10 m		Longest Radius of 30 kt
	Error (km)	Error (hPa)	Relative Error (%)	Error (m/s)	Relative Error (%)	Error (km)	Relative Error (%)
R0	106.2	42.9	4.7	−11.8	23.3	−59.1	13.8
R1	98.6	37.2	4.0	−8.4	17.0	−19.1	7.9
R2	110.1	44.3	4.8	−13.9	27.1	−74.7	17.4
R3	93.0	40.9	4.4	−10.7	21.4	−39.7	9.4

. The differences between R0 and R2 are small. These track results suggest that, for both TCs, the wave-affected surface exchange coefficients have a greater effect on the simulated TC track than does wave-induced mixing.

4.1.2. TC Intensity

Figure 2b,c depicts the time series for intensity (the minimum sea surface pressure [SSP], and maximum wind speed at 10 m) for Shanshan. The best track data show that Shanshan intensified between 00:00 UTC and 18:00 UTC on 4 August 2018, then maintained a maximum sustained wind speed close to 36 m/s. In R0, the intensity is slightly overestimated with small biases (Table 2) in the simulated minimum SSP (and maximum winds at 10 m), relative to the best track data. When the wave-affected surface exchange coefficients are used in R1, the intensity of Shanshan is strongly overestimated, with a lower (or smaller) minimum SSP and higher maximum wind speeds at 10 m than the best track data. The simulated maximum wind speed at 10 m (and minimum SSP) in R1 is excessively strengthened (deepened), reaching a relatively high wind speed of 50 m/s (low pressure of 945 hPa) at 06:00 UTC on 6 August 2018, then weakens (rises) gradually. In R2, which includes wave-induced mixing, the maximum wind speed at 10 m rises more slowly and reaches typhoon grade later than in the best track data, then weakens. Wave-induced mixing generally weakens the TC intensity; this is because of the enhanced mixing, driven by wave orbital motion, which leads to cooler SSTs and ultimately reduces the heat flux from the ocean to the air (see detailed discussion in Section 4.3 and Section 4.4). In R3, both the wave-affected surface exchange coefficients and wave-induced mixing are taken into account. The results for R3 show that the combined wave-related effects result in a relatively small error for the minimum SSP and maximum winds at 10 m compared with the best track data.

The intensities simulated for Megi are weaker than the best track data for all four experiments (Figure 3 and Table 2). Comparison with R0 shows that the wave-affected surface exchange coefficients in R1 have a positive effect on the simulated intensity, leading to the deepest minimum SSP and the strongest maximum winds at 10 m among the four simulations. The wave-induced mixing in R2 has a negative impact on the simulated intensity, relative to R0, and results in the shallowest minimum SSP and weakest maximum winds at 10 m. The intensity in R1 strengthens more quickly and follows the observations more closely than in the other experiments. In R2, wave-induced mixing leads to slow development of the minimum SSP and maximum 10 m winds (same scenario in Shanshan), suggesting that wave-induced mixing is not conducive to TC intensification and maintenance. In R3, the impacts of the two wave-related processes counter each other and the combined effect is neutral.

Taken overall, the results for track and intensity show that the coupled model with only wave-induced mixing seems best for Shanshan, but the model with only wave-affected coefficients performs best for Megi. This may be due to the intrinsic limitation of dynamical model for TC simulations. Current dynamical models for TC intensity predictions or simulations have exhibited a tendency to over intensify weak storms and under intensify strong systems due to our insufficient understanding of the coupled air–sea-wave system [82]. For Shanshan, which has a weak intensity, the wave-induced mixing performs a critical role in intensity predictions and the intensity forecasts are improved with the effect of wave-induced mixing included in the model. For Megi, which has an extremely high intensity, the original model (R0) does not perform well. The wave-affected coefficients including the wave-related small-scale processes are conducive to TC intensification by enhancing the air–sea heat fluxes, but the intensity forecasts with the wave-affected coefficients are still weaker than the best track data. It is likely that limitations in the model physics will have to be adequately resolved before skillful intensity forecasts become routine for strong or super typhoons. Another possible source of error in the intensity forecasts or simulations for these two typhoon cases is the model settings including the spatial and temporal resolution, and the frequency of data exchange between the three sub-model components.

4.1.3. TC Size

At 08:12 UTC on 6 August 2018, the WindSat radiometer recorded 10 m wind speed observations for Shanshan (Figure 4a). Figure 4b,c,e,f show the simulated 10 m winds for our four experiments. The black lines in these panels represent the radius of 15.4 m/s (30 kt) winds (defined by JMA as describing the TC size). We note that data from radiometers usually have large uncertainties at high wind speeds (>20 m/s) due to the lack of reliable ground observations for calibration (and validation) and the impact of the rain that is generally associated with a TC [83,84]. Therefore, we use WindSat wind speed observations that are below 20 m/s to validate the simulated pattern for the TC size. As shown in Figure 4b,c,e,f, all the simulations indicate that the radius on the right side of the track direction (the eastern side of the TC center) is larger than that on the left side (the western side of the TC center), which is consistent with the observations. However, the TC size is overestimated in R1 relative to the observations, whereas the modeled size in R2 is underestimated. Compared with the best track data, the simulated TC size for the longest radius of 15.4 m/s winds in R1, which includes the wave-affected coefficients, agrees well with the observation (Figure 4d), with only very small errors (Table 2). In contrast, R2, which considers the wave-induced mixing, leads to quite a large underestimation for the longest radius of 15.4 m/s winds, relative to the best track data. Similar to R2, in the results from R3 (which include both wave-related effects), the simulated radius is generally underestimated and much smaller than in R0. In our comparison of the simulated and best track TC sizes, we focus on the longest radius of 15.4 m/s wind speed, as this parameter represents the region of maximum influence for a TC and is used for TC monitoring, warnings, cost–benefit analyses, and damage assessments.

The ASCAT scatterometer observed the wind fields of Megi at 13:12 UTC on 17 October 2010 (Figure 5a), and we use these observations to assess the pattern of TC size (radius of 15.4 m/s winds) for Megi. As for the WindSat radiometer, the ASCAT scatterometer cannot provide reliable wind speed data under high wind speed conditions (greater than 25 m/s) [85,86]. The ASCAT data in Figure 5a show that the TC size on the right side of the track direction (the northern side of the TC center) is larger than that on the left side (the southern side of the TC center), despite only half of the wind field were caught up. The TC sizes simulated in all four experiments capture the patterns seen in the ASCAT observations (Figure 5b,c,e,f). Compared with the best track data, we found that the simulated longest radius for 15.4 m/s was underestimated by different amounts in all four simulations (Table 2). The bias is smallest in R1, where the simulated radius is only 7.9% lower than the best track data. In R0, R2, and R3, the underestimation is much greater (Table 2).

For both Shanshan and Megi, the simulated size results suggest that the wave-affected surface coefficients have a significant positive impact on TC size, whereas the wave orbital induced mixing has a negative effect. The combined effect of wave-affected surface coefficients and the wave orbital induced mixing is different for the two TCs. As Figure 4d and Figure 5d show, the simulated longest radii of 15.4 m/s in R3 are smaller than those in R0 for Shanshan, but they are greater for Megi. Similar results are seen for the simulated intensity (Figure 2c and Figure 3c). The modeled maximum wind speeds at 10 m (and the minimum SSP) in R3 are lower (shallower) than those in R0 for Shanshan, but they are higher (deeper) than in R0 for Megi. These results suggest that wave-induced mixing effects dominate over the effects of the wave-affected exchange coefficients for Shanshan, and that the opposite is true for Megi. Comparing the different wave-induced mixing effects simulated for Shanshan and Megi, we see that, when wave-induced mixing is considered in R2, the intensity (size) of Shanshan weakens by 10.4% (11.1%) compared with R0; however, the intensity (size) of Megi reduces by only 5.0% (4.1%) relative to R0. The simulated TC intensity and size are sensitive to SST [9,10,66], and the SST cooling due to wave-induced mixing depends on the vertical temperature structure of the ocean (discussed in Section 4.3). In the case of Shanshan, wave-induced mixing results in a strong decrease in SST owing to the shallow MLD and cold subsurface water (below mixed layer). This leads to a significant reduction in air–sea heat fluxes and thus weakens the TC intensity (and size). In contrast, the effect of wave-induced mixing is relatively small for Megi due to the locally warm subsurface water. This is discussed in more detail in Section 4.3 and Section 4.4.

4.2. Validation for Surface Waves and Winds Using Altimeter Observations

In this subsection, we validate the model output for 10 m wind speeds and surface waves using altimeter observations. For Shanshan, we use Jason2, Jason3, and Sentinel Ku band data, and we use Cryosat, Envisat, Jason1, and Jason2 Ku band data for Megi. The ground tracks for these altimeters are shown by grey lines in Figure 2a and Figure 3a. Figure 6 and Figure 7 exhibit comparisons between the modeled and observed 10 m wind speeds for Shanshan and Megi, respectively. In general, the agreement is good and the simulations are strongly correlated with the observations for all experiments. However, when only the wave-affected surface coefficients are introduced (R1), the 10 m wind speeds are overestimated with a positive mean error (ME). When only wave-induced mixing is considered (R2), the 10 m wind speeds are slightly underestimated. When both the wave-affected surface coefficients and wave-induced mixing are taken into account, the overestimate in R1 and the underestimate in R2 are reduced.

Figure 8 and Figure 9 display the comparison between the simulated and altimeter-observed significant wave height (SWH) for Shanshan and Megi, respectively. These show that the model results agree well with the observations, with a strong correlation. The bias between the modeled SWH and the measurements is between 0.57 m and 1.09 m, indicating that SWH is overestimated in all experiments. Olabarrieta et al. [76], Wu et al. [87], and Zhang W. et al. [10] obtained similar results in studies on TC using COAWST. Olabarrieta et al. [76] attributed this to the model spatial resolution, the model accuracy in different regions, and the method used to derive SWH from the altimeter data. Zhang W. et al. [10] suggested that the bias could be related to the imperfection of wave dissipation source terms in the wave model. The simulated SWHs in R1 are higher than those in R0, reflecting the enhancement of 10 m wind speeds in R1 due to the effect of the wave-affected surface coefficients. In contrast, the wave-induced mixing in R2 results in lower wind speeds than in R0, leading to smaller SWHs in R2 than in R0. However, the reduction in SWH in R2 relative to in R0 is not significant for Megi.

4.3. SST

In this subsection, we analyze the simulated SST results and verify them through comparison with RSS observations. Figure 10 displays SST patterns on 6 August 2018 for Shanshan for the different experiments and the RSS observations. It shows that the SSTs simulated in R2 and R3, both of which consider wave-induced mixing and agree closely with the observations. SST is overestimated in R0, with a bias of ~0.6 °C. This bias is slightly compensated for R1, which considers wave-affected exchange coefficients that lead to higher wind speed. The SSTs simulated for Megi in R2 and R3 match the RSS data reasonably well (Figure 11). Similar to the simulated SSTs for Shanshan in R0 and R1, the SST simulated for Megi in R0 and R1 are ~0.5 °C and 0.4 °C higher than the observed SST, respectively.

Comparing the four modeled SST results shows that, when wave-related small-scale processes are considered using the wave-affected exchange coefficients in R1, the SST is only ~0.1 °C smaller than in R0, despite the fact that considering the wave-affected exchange coefficients results in higher wind speeds. The decrease in SST is stronger in R2 when wave-induced mixing is included. However, the magnitude of the SST reduction due to wave-induced mixing differs between Shanshan and Megi (Figure 10d and Figure 11d). Figure 10d shows that, the SST averaged over 300 km radius inner core region along Shanshan center location, is more strongly reduced in R2 (~1.0 °C) than in R0. The decrease in SST, averaged over 300 km radius inner core region along Megi center location, is weaker in R2 than it is for the case of Shanshan (~0.2 °C; Figure 11d). The SST reduction (due to wave-induced mixing) over the whole simulation domain also shows the similar behavior in these two TC cases (figure not shown due to space constraints).

The different magnitudes for the SST decrease due to wave-induced mixing in our two TC cases are mainly due to differences in the vertical temperature structure of the ocean in the two cases. As shown in Figure 12, the mixed layer in the Shanshan simulations is shallow before the arrival of Shanshan, with an MLD of ~15 m. Below the mixed layer is a strong thermocline. Megi occurred to the south of Shanshan, and the mixed layer simulated for Megi was deep (~40) prior to the arrival of Megi, and the thermocline under Megi is relatively weak. Despite the differences in their MLDs and thermoclines, the SSTs are similar for the Shanshan and Megi simulations prior to the arrival of the TCs (29.0 °C and 29.6 °C, respectively). The wave states (wave height, wave period, and wavelength) are also similar for Shanshan and Megi (figure for wave state is not shown due to space constraints). The penetration depth for wave-induced mixing is of the order of the wavelength [20]. Under TC conditions, the wavelength may reach approximately 100 m for a wave period of 12 s, so the turbulence generated by surface waves penetrates deeply and entrains colder water from below the mixed layer base or thermocline, leading to SST cooling. At a depth of 100 m (the order of wavelength), the water temperature is 25.5 °C in Megi and cooler (19.5 °C) in Shanshan. This suggests that the water entrained from below the mixed layer base (owing to wave orbital motion) is warm in Megi, with a relatively small difference to the SST, so the reduction in SST is small. In contrast, the degree of SST cooling is greater in Shanshan because the temperature difference between the water below the mixed layer and the SST is greater.

4.4. Heat Flux

In this subsection, we present the modeled air–sea heat fluxes in different experiments. Unlike previous subsections, here we do not compare the modeled results with other products as there are no available observed resources to be applicable under these two typhoons. The focus here is comparison of heat fluxes across different schemes, and to analyze the effect of wave-related processes on the air–sea heat exchange. Figure 13 and Figure 14a,b show the latent and sensible heat flux distributions and evolutions for Shanshan. When the wave-affected exchange coefficients are used in R1, the latent and sensible heat fluxes increase by 17.5% and 12.0%, respectively, compared with R0. When wave-induced mixing is considered in R2, the latent and sensible heat fluxes decrease significantly by 36.1%, and 39.6%, respectively (relative to R0), owing to the SST cooling that is driven by wave-induced mixing under strong thermocline conditions (discussed in Section 4.3). In R3, when the wave-affected exchange coefficients and wave-induced mixing are both considered, the latent and sensible heat fluxes reduce by 25.7% and 26.2%, respectively (relative to R0), suggesting that wave-induced mixing performs a more dominant role than wave-affected exchange coefficients in modulating heat transfer for Shanshan.

Figure 14c,d and Figure 15 show the latent and sensible heat flux distributions and evolutions for Megi. Compared with R0, the latent and sensible heat fluxes in R1 are enhanced by 28.4% and 22.1%, respectively. In R2, the latent and sensible heat fluxes reduce slightly (by 3.2% and 3.7%, respectively) owing to the minor SST decrease driven by wave-induced mixing when the subsurface (below the mixed layer) water is warm (see Section 4.3). In R3, when both the wave-affected exchange coefficients and wave-induced mixing are considered, the latent and sensible heat fluxes increase by 24.3% and 14.7%, respectively (relative to R0), implying that the wave-mediated exchange flux (or wave-affected exchange coefficients) performs a greater role in modulating heat flux for Megi than wave-induced mixing.

The above results for Shanshan and Megi show that including the wave-affected exchange coefficients results in enhancing the estimated heat fluxes and has a positive impact on TC intensity and size. The wave-affected exchange coefficients implicitly include the wave-related small-scale processes (wave breaking, sea spray, and foam) which increase significantly the air–sea heat exchange under high wind speeds. Note that both COARE 3.0 and formulations of Komori et al. [16] implicitly contain wave-driven processes, but COARE 3.0 does not seem applicable for high wind speeds. For moderate and low wind speeds (greater than about 5 m/s and lower than about 25 m/s), wave steepness or wave age performs a dominant role in the surface roughness [61]; however, the wave-related small-scale processes are not yet apparent. COARE 3.0 is obtained at moderate and low wind speeds, therefore, the wave-related processes (such as wave breaking, sea spray, and foam) dominating the air–sea interface are not considered sufficient. Wave-induced mixing leads to a decrease in the estimated heat fluxes and has a negative effect on TC intensity and size. Note that the degree of wave-induced mixing for modulating the TC system depends on the vertical ocean temperature structure.

5. Conclusions

In this study, the effects of surface waves on TC systems have been investigated through numerical simulations using a coupled ocean–atmosphere–wave model (COAWST) and a comparison with available observations. Two factors were considered: wave-induced mixing and wave-affected exchange coefficients. Wave-induced mixing was parameterized by introducing turbulence production due to wave orbital motion [41] into a two-equation turbulence closure scheme. Wave-affected surface exchange coefficients observed at extremely high wind speeds in a laboratory by Komori et al. [16] were implemented into the coupled model. Typhoon Shanshan (2018) and Super Typhoon Megi (2010) were used as case studies.

It is shown that wave-affected surface exchange coefficients can enhance heat fluxes and have a significantly positive effect on TC intensity and size and are conductive to TC strengthening. In contrast, wave-induced mixing has a negative impact on TC intensity and size and does not promote to TC intensification and maintenance. It is found that the magnitude of the impact of wave-induced mixing on a TC system depends on the local ocean vertical temperature profile. Wave-induced mixing can extend to a depth comparable to the wavelength (~100 m) under TC conditions [20], and the mixing induced by long waves penetrates deeply enough to enhance turbulent entrainment near the mixed layer base, deepening the mixed layer and leading to SST cooling. When the thermocline is strong and the subsurface water below the mixed layer is cold, wave-induced mixing results in strong SST cooling and a significant reduction in heat fluxes, and this effect ultimately dominates over the effects the wave-affected exchange coefficients. When the thermocline is weak and the water below the mixed layer is warm, then wave-induced mixing has a relatively small effect on TC intensity and size, and wave-affected exchange coefficients perform a dominant role in modulating the TC system. Note that as the cases used in this study are limited quantitatively, these conclusions are preliminary and subjected to be examined in more TC cases of various properties, such as tropical depressions, decaying TCs, and TCs that move quickly or slowly.

Maybe the experiment (R3) that considers all the effects of surface waves performs not so perfectly, rather we focus on the physical processes of air–sea interaction related to the surface waves and assessing the relative and combined effects of wave-induced mixing and wave-affected surface exchange coefficients on TCs. Although our present model results from R3 seem to have limited improvement compared to R0, we have a clearer and deeper understanding of the complex sea-air-wave interaction under TC conditions. There is still much work to be completed for the improvement of the fully coupled air–sea-wave model system.

Recent studies have shown that, under extreme conditions, such as a TC, the drag coefficient depends on the wave and sea state [64,88]. It is more suitable to use a more complicated parameterization scheme including the wave parameters for the investigation of the effect of wave-affected surface exchange coefficients on TCs. In this study, we did not adopt a wave- or sea-state dependent drag coefficient, instead using the wave-affected exchange coefficients that were derived from laboratory data and are expressed as functions of 10 m wind speed [16] because the available wave- and/or sea-state dependent parameterizations are uncertain due to the difficulty of making observations under TC conditions and the scarcity of field data. More studies with reliable and complicated scheme including the wave parameters are needed in future work when more reliable and complete observations of ocean, atmosphere, and surface waves are obtained. However, we note that laboratory observations do not necessarily reproduce the real environment, and small-scale wave-related processes in the air–sea boundary have not been fully clear and are not explicitly represented. Our study provides a framework and reference for future TC prediction and research.