1. Introduction
Soil moisture content variation directly impacts shear strength, volume change, and crack formation within geo-structures such as highway slopes and embankments. Therefore, soil moisture content variation within soil bodies is a critical factor influencing failure mechanics, causing landslides, shallow slide failures, and surface erosion [
1,
2,
3,
4,
5,
6]. Central Mississippi’s highway slopes and embankments are subject to increased risks from soil moisture variation due to the presence of expansive clay [
7,
8]. Rainfall and temperature patterns induce wet–dry cycles that cause and propagate cracks [
2,
9] and cause high volume changes in expansive clay. Near-surface soil moisture content variation and matric suction are significant factors in the frequent shallow slope failures observed on Mississippi’s highway slopes [
10].
Highway embankment fill slopes in Mississippi are often built with expansive Yazoo clay, which can be easily susceptible to shallow and deep-seated slide failures, especially during increased rainfall [
2,
7,
8,
9]. Mississippi Department of Transportation’s state studies report over forty annual side slope (embankment) failures. Rainfall can increase the soil moisture content, lowering the matric suction and increasing the pore water pressure, which reduces the soil’s shear strength and friction angle, making it more susceptible to failure.
As a result, constant monitoring of soil moisture content is essential for a successful geotechnical asset management program. Soil moisture content (gravimetric or “w”; volumetric or “θ”) monitoring is traditionally done through single-point or precise location measurements [
11]. The gravimetric method of soil moisture measurements is widely accepted for accurate measurements of “w”. However, the gravimetric method is labor-intensive and destructive.
Capacitance probes, soil moisture in situ sensors such as Time Domain Reflectometry (TDR), and Frequency Domain Reflectometry (FDR) are other contact-based methods for measuring θ. Tensiometers, FDR, and TDR have largely been implemented in agricultural and grassland management applications to monitor moisture content variations [
12,
13]. Despite producing good results, these methods are quite expensive [
14,
15]. In situ point monitoring techniques such as moisture sensors lack spatial resolution and fail to give a complete picture of soil moisture variation across the slopes and embankments [
14]. Installation of the sensors is expensive; moreover, the sensors come with a life span and are susceptible to premature failure due to wear and tear.
In contrast, Unmanned/Uncrewed Aerial Vehicles (UAVs) have higher spatial and temporal resolutions, enabling more efficient monitoring of site conditions [
14,
16]. UAVs are increasingly used in low-altitude remote sensing applications and offer many benefits such as high spatial and temporal resolution and high-quality georeferenced data [
17,
18]. Several studies have used UAV images to estimate soil moisture content [
17,
19,
20]. Visible color spectra of digital images have been used to predict soil moisture content [
14,
20,
21,
22,
23].
UAV optical images combined with machine learning methods have also been successfully implemented to predict soil moisture content. For instance, soil moisture prediction models have been developed using RGB images and artificial neural networks [
12,
24]. Machine learning techniques implemented for soil moisture prediction from remote sensing data include Multiple Linear Regression (MLR) [
14], Support Vector Regression (SVR) [
22,
25,
26], and Extreme Gradient Boosting (XGB) [
27,
28,
29]. High-resolution UAV images in tandem with XGB have been applied to infer soil moisture content in precision agriculture applications [
30].
Hajjar et al. [
22] evaluated MLR and SVR models to predict moisture levels based on RGB color model pixels extracted from soil digital images and known moisture levels at a vineyard in Lebanon. He et al. [
27] and Tao et al. [
29] evaluated Random Forest and XGB models for predicting soil moisture using inputs from earth observatory satellite systems’ imagery. In both studies [
27,
29], prediction results were evaluated in terms of performance metrics such as Root Mean Square Error (RMSE) and correlation coefficient, and XGB provided better results than other models. Kim et al. [
14] developed a soil moisture content estimation equation based on the RGB color of the soil.
Alternatively, thermal sensing is another proven method to estimate soil moisture content. The underlying concept here is that the thermal inertia of the soil is negatively correlated with the variation of θ [
31]. Land surface temperatures obtained from thermal images can be used for predicting soil moisture [
31,
32,
33].
Inferencing soil moisture using remote sensing data and machine learning algorithms has been implemented in agriculture [
16,
20,
22,
23,
30], hydrology [
12,
22,
25], and grassland management applications [
17,
24].
However, using UAV-based images to characterize the soil moisture content of highway slopes and embankments is rare and needs further exploration. The soil moisture content prediction models implemented by other studies are specific to the local soil types, biological and chemical conditions, and local climate [
14,
22,
23]. The lack of similar studies for Mississippi’s soils is an added motivation to undertake this study focusing on soil moisture estimation for Mississippi’s highway embankments and slopes.
The current study’s objective was to develop two separate methods to predict soil moisture content (‘θ’ or ‘w’) using UAV optical and thermal images combined with machine learning and statistical modeling. The first method used RGB color values from UAV-captured optical images for predicting θ. Support Vector Machine for Regression (SVR), Extreme Gradient Boosting (XGB), and Multiple Linear Regression (MLR) models were trained and evaluated for predicting θ from RGB values. The second method used Diurnal Land Surface Temperature (ΔLST) variation from UAV-captured Thermal Infrared (TIR) images to predict θ. The two methods (RGB vs. θ and ΔLST vs. θ) were developed independently, and integrating the two methods was not within the scope of this study. This investigation used a DJI-Matrice 200 V2 drone with FLIR’s Zenmuse-XT2 dual sensors to capture optical and thermal infrared images of highway embankments in Jackson, MS, USA.
2. Materials and Methods
2.1. Highway Embankment Site Locations
Highway embankment sites were chosen within a 25-mile radius of Jackson, Mississippi (
Figure 1). The slopes of Sowell Road, Terry Road, and Metro Center were selected as representative highway embankments for the region. Multiple surveys using UAVs were carried out at these sites.
2.2. Study Design
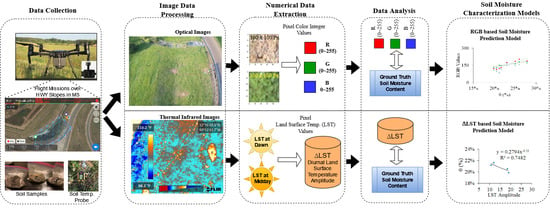
The schematic of the study is presented in
Figure 2. Two different methods were implemented to develop soil moisture prediction models. The first method used raw RGB color values from optical images to train Machine Learning (ML) models to infer θ. In the second method, diurnal LST differences determined from TIR were used to build regression models to estimate θ.
Deriving the soil moisture from the optical images required examining the underlying pattern between the RGB color integer values of the pixels and ground truth θ. Since the underlying pattern’s rules are unclear for RGB vs. θ correlations, machine-learning approaches were employed to solve this problem. Specifically, SVR, XGB, and MLR methods were evaluated for θ inferencing using RGB data.
On the other hand, developing the thermal image-based θ prediction model relied on the underlying relationship between the near-surface soil thermal inertia and θ. Radiometric information embedded within the pixels of thermal infrared images was extracted using the FLIR Thermal Studio application. Then, by implementing regression modeling, the thermal inertia from infrared images captured at dawn (low temperature) and midday (peak temperature) were used to infer θ.
2.3. UAV Data Acquisition
UAV flights were carried out by some of the authors who are FAA part 107 licensed small Unmanned Aerial Systems (sUAS) pilots who captured all the aerial optical and thermal imagery from the three sites used in this study. Images were captured using a DJI-Matrice 200 drone. The integrated 3-axis gimbal mechanism on the UAV platform helped to steady the camera during flight, reducing vibration-induced blur in the aerial photos. The UAV was flown at 100 to 200 ft (~30–60 m). Mobile applications recommended by the drone manufacturer were used for flight planning and control. The gimbal’s pitch range was adjustable while in flight, ranging from −90° (i.e., nadir) to +30°.
A Zenmuse-XT2 Dual sensor camera with an optical camera and an uncooled micro-bolometer FLIR thermal sensor was used. The FLIR thermal sensor captures surface radiance energy by passing and collecting the Long Wave Infrared (LWIR) band of the electromagnetic spectrum from the land. Optical and thermal images were acquired on several occasions at three sites over two months in the summer of 2022. Thermal images were captured at midday and dawn to record the diurnal land temperature difference.
2.4. Ground Truth Soil Moisture Content
Near-surface soil samples at 1″ to 6″ (~2.5 to ~15 cm) depth were collected from three Regions of Interest (ROI) at each of the three sites, making a total of nine ROIs. These ROIs, designated as I1, I2, and I3 at each site, are presented in
Figure 3,
Figure 4 and
Figure 5.
ROIs selected included Bare Ground (BG), Vegetation Covered (VC), and mixed BG plus VC locations. Such multiclass ROIs were purposely selected to help generalize the θ inferencing capabilities of the developed models across both types of image classes. The average gravimetric soil moisture content (
) for each ROI was determined in the laboratory per ASTM (2010) Standard D2216 as described in the following steps. Step 1: weigh a labeled empty container (
c) with the lid on. Step 2: add the collected moist soil into the container, close the lid, and measure weight (
). Step 3: remove the lid and place the container with the soil sample in the oven for up to 24 h at a temperature of 230° F (~110° C). Step 4: remove the container from the oven, close the lid, and measure the weight (
). Steps 1 through 4 were performed for soil samples collected from nine ROIs in total from all sites. The ground truth
% was determined by Equation (1).
where
= gravimetric soil moisture content, (
= weight of water determined by (
), and
= weight of solids determined by (
),
The ground truth volumetric moisture content (θ) was determined using Equation (2).
where θ = volumetric soil moisture content,
is gravimetric soil moisture content,
is the specific gravity of 2.7, and the degree of saturation S of 50% was considered based on a past study at these sites [
7].
Ground truth
and θ determined at each site at the selected ROIs are presented in
Table 1.
2.5. UAV Optical Image Data Processing and Analysis
The UAV-captured optical images were examined, and appropriate aerial images without any blur, shadows, and distortions were selected for RGB extraction. The optical image resolution was 3000 × 4000 pixels (px), and the ground resolution of the optical images was approximately 0.03 ft. (0.009 m)/px. Three ROIs per site ranging from 80 × 80 px ~100 × 100 px areas were identified, making a total of nine ROIs from three sites. These ROIs were at the same locations from where soil samples were collected to determine ground truth soil moisture content. The ROIs selected included some bare-ground areas as well as vegetation-covered areas.
The Metro Center slope image and the three bare-ground ROIs are presented in
Figure 3. The Terry Road slope image with the multiclass ROIs (one bare ground, one Vegetation covered, and one mixed class) are presented in
Figure 4. Such multiclass ROIs were selected to help generalize the θ inferencing capabilities of the developed models across different types of image classes. The Sowell Road slope image with the three vegetation-covered ROIs are presented in
Figure 5.
2.5.1. RGB Extraction and Visualization
The raw RGB color integer values embedded in each pixel of the optical images are a combination of integer values that range from 0 to 255. RGB raw values from every 10th pixel in horizontal and vertical directions were extracted from the 100 × 100 px ROIs. From the 9 ROIs (3 per site), a total of 879 rows of RGB data vectors were extracted. Out of the 879 data vectors, 381 belonged to the Bare Ground (BG) class, 400 to the Vegetation Covered (VC) class, and 98 to the mixed class.
The raw RGB values extracted from the ROI were compared with ground truth θ for the corresponding ROI.
Figure 6a presents the variation of all 879 RGB data vectors vs. the average θ extracted from the 9 ROIs off the 3 sites. After averaging, the multiclass RGB data vectors boil down to nine instances, with four belonging to the bare ground class, four to the vegetation covered class, and one to a combined class. The variation of RGB averages with average soil moisture content at their respective ROIs is presented in
Figure 6b. The average RGBs at each ROI and corresponding ground truth soil moisture content values are also presented in
Table 2.
The RGB average values variations with θ separated by the BG and VC classes are presented in
Figure 7.
Figure 7a represents the average RGB vs. θ for bare-ground ROIs, and
Figure 7b represents average RGB values vs. θ for vegetation-covered ROIs. The red color is higher for the bare ground class, and the green color is higher for the vegetation-covered images, which is plausible. Furthermore, the near-surface soil moisture content was observed lower in vegetation-covered slope areas. In contrast, the near-surface θ was observed higher on bare-ground areas of the slope. This observation indicates that vegetation captures the soil moisture from the near-surface soil, resulting in lower near-surface.
2.5.2. Data Cleaning
As the moisture content increases, the soil color should also increase [
21] (Persson, 2005). However, for the Bare Ground (BG) class in
Figure 7a, the RGB variation does not follow this logic and has higher color values for low soil moisture content, mainly due to the outliers. Similarly, it is also evident from
Figure 6b that the RGB values obtained from metro center ROI#3 behaved as outliers and therefore were removed from the RGB dataset.
Furthermore, the RGB dataset was further examined, and more outliers were identified to avoid errors in the soil moisture content estimating models. The following procedure was implemented to remove the outliers. Firstly, the sums of the R, G, and B values were calculated for each of the 879 rows. Then, the sums of the RGB values were divided into 4 quartiles, and 25th, 50th, and 75th percentiles were calculated. The RGB sum values lesser than the 25th percentile and greater than the 75th percentile were considered outliers and eliminated from the dataset. The mixed class data from Terry Road ROI#3 were also left out from the cleaned-up dataset. After removing the outliers, 370 rows of RGB data vectors remained, consisting of 169 BG class and 201 VC class. All subsequent results were derived using the cleaned-up dataset without outliers. The 370 rows of RGB, together with the ground truth soil moisture content, were used to train the machine learning models. The 370 RGB data vector distribution is presented in
Figure 8.
2.5.3. Machine Learning Methods for Soil Moisture Content Characterization Using RGB Data
A total of 879 rows of RGB data were extracted from the optical image ROIs for the 2 classes of bare ground and vegetation covered. The final cleaned-up dataset was about 370 rows of RGB values and corresponding ground truth moisture content values. The ML models SVR, XGB, and MLR were developed using the cleaned-up dataset to infer soil moisture content. Each ML method was trained in different ways in terms of RGB data classes: one with combined classes of Bare Ground (BG)and Vegetation Covered (VC), the second with the bare ground class alone, and the third with the vegetation covered class alone. Jupyter Notebook and the Python programming language were used to perform data cleaning and visualization and to develop the machine learning models.
Training-Test Split: The cleaned-up dataset was split into 80% training and 20% test samples using the train_test_split function imported from the sklearn library to develop the machine learning models. For the VC+BG combined class dataset, out of the 370 data vectors, 296 RGB data vectors were used for training and 74 data vectors were used for testing. For the BG-only dataset, out of the 169 data vectors, 135 RGB were used for training and 34 were used for testing. For the VC-only dataset, out of the 201 data vectors, 160 RGB data vectors were used for training and 41 data vectors were used for testing.
Support Vector Regression (SVR): A Support Vector Machine (SVM) is a proven machine learning algorithm for classification and regression. When used for regression, it is known as SVR. SVR has been used to develop soil moisture prediction models based on RGB values for lab-scale models [
22] (Saad Hajjar et al., 2020) and for the region scale using satellite imagery [
12] (Ahmad et al., 2010). In this study, e-SVR was implemented to predict soil moisture from the RGB input features. The support vector regression in its standard form is presented in
Figure 9. SVR allows the user to decide how much error in the model is acceptable, and it will locate a suitable line in two-dimensional problems (or hyperplane in higher dimensions) to fit the data. In
Figure 9, epsilon (e) represents the allowed error margin. Epsilon can also be visualized as the tube that determines the hyperplane width.
The goal would be to predict data within the given margin of error (e). Variables beyond the margin lines are assigned a deviation value called slack (ξ). The other significant parameters include kernel, regularization factor C, and gamma. RBF kernel function was used in this study, which allows implementing regression using hyperplane on a higher dimension. The most widely used regularization factor is C = 1.0 [
34]. The higher the C, the better the fitting on the training dataset. However, a higher C impedes the model’s generalization ability and affects the test dataset predictions.
Extreme Gradient Boost (XGBoost or XGB) method: XGB is a tree-based ensemble machine learning algorithm that improves on the gradient boosting framework by incorporating certain precise approximation algorithms [
35]. It offers improved prediction power and performance. Ensemble machine learning modeling approaches such as XGB are powerful models made up of a group of weaker base models [
36]. It uses gradient boosting to construct machine learning algorithms. It is an advanced implementation of the Gradient-Boosted Regression Tree (GBRT) [
37], which is a sequential ensemble method that adds several base regression trees over time to increase the capacity of the entire model. This ensemble approach can be used for regression. High-resolution UAV images in tandem with XGBoost algorithm have been applied to infer soil moisture content [
30]. Among the many parameters within XGBoost architecture, the following make a difference to the prediction results:
Gamma: loss function varying between 0 and 1.
Max Depth [0~infinity]: Maximum depth of a tree. A default value of 6 is set but varied up to 100 and observed for changes. Increasing this value will make the model more complex and more likely to overfit.
Min Child Weight [0~infinity]: for linear regression, this refers to a minimum number of instances that are needed in each node.
Learning Rate [0~infinity]: the model’s learning rate determines how quickly it adapts to the given problem and is, by default, 0.3.
Multiple linear regression method: Multiple linear regression models are an excellent choice for simple problems for quantifying relationships between a set of independent variables (features) and a single dependent variable (target). Therefore, MLR models were implemented for soil moisture prediction using RGB values in this study. A typical MLR model is shown in Equation (3).
where y is the target and x
0 = 1, {x
1~x
n} are input features, a
0 is the slope intercept, and {a
1~a
n} are the coefficients. Similar to the other machine learning models, three multiple linear regression models were developed, one for the combined class model (MLR1), one for the bare ground class (MLR2), and one for the vegetation class (MLR3).
2.6. UAV Thermal Infrared (TIR) Image Processing
The thermal sensor payload captured TIR images with a 640 × 512 px resolution. The TIR images were processed through the FLIR Thermal Studio application to obtain pixel temperature values. The temperature values were then corrected (commonly referred to as calibration) for the ambient conditions. The radiometric data were calibrated for the observed humidity, ambient temperature, reflected temperature, and emissivity.
2.6.1. TIR Temperature Calibration, Verification, and Optimization
TIR Calibration: Thermal sensor calibration is a prerequisite for accurate radiance and absolute temperature measurements for thermography applications. The FLIR Zenmuse XT2 (FZ2) thermal sensor used in this study is an uncooled microbolometer type, and the manufacturer calibrates it during production to carry out infrared radiance and temperature measurements. FZ2 has been drift compensated by the manufacturer, which means that the camera compensates the output for variation in the camera’s internal temperature. FZ2 has also gone through verification against a standard traceable black body. This verification process aims to compare the radiance from the TIR against a known traceable blackbody ground truth, validate the temperature measurements, and adjust the sensor accordingly. The TIR images captured by FZ2 were post-processed in the FLIR Thermal Studio software application. During post-processing, the absolute land surface temperature from raw thermal images is read and converted to infrared radiance emitted from surfaces using Planck’s Equation.
We further verified the thermal images and adjusted them to specific field conditions by adjusting the object parameters: ambient temperature, relative humidity, emissivity, and reflected temperature. For the surficial soil, an emissivity of 0.8–0.95 was used based on published data from FLIR. Relative humidity and ambient temperature values were obtained from the data published by NOAA for the nearest weather station for the time of the day the UAV flight occurred. The weather station parameters were input into the FLIR Thermal Studio application, which has inbuilt algorithms that correct the LST based on the object parameter values. The reflected temperature adjustment was performed by following the standard reflector test method explained in the following paragraph.
Reflected temperature is any thermal radiation originating from other objects that reflects off the target measured. The value of the reflected temperature should be calculated and programmed into the camera’s parameters to make it possible for the software to compensate and ignore the effects of this radiation to obtain the actual surface temperature of the soil. The reflected temperature is related directly to the emissivity of the same object; higher emissivity objects tend to produce less reflected temperature influence. Therefore, objects with a lower emissivity (such as aluminum) and high reflectance can provide an accurate measure of the atmospheric reflected temperature.
ASTM E1862 describes the commonly adapted reflector method using aluminum foil (1 ft wide × 2’ long) for assessing the reflected infrared energy from the atmosphere [
38]. This method has been successfully implemented in previous relevant studies by [
39].
In the current study, aluminum (AL) foil was placed on the field during the UAV flight, as shown in
Figure 10. The UAV-mounted thermal sensor FZ2 captured the temperature of the aluminum foil reflector. In post-processing, the emissivity value of the AL foil is set to 1, and the distance is set to 0. Then, the average surface temperature reading of the AL foil reflector is measured. This surface temperature value of the AL foil reflector is assigned to its reflected temperature, and the foil’s surface temperature measurement is retaken. The resulting temperature provides the actual atmosphere-reflected temperature for the specific site on that specific day. All thermal images captured on that site at a specific time were adjusted according to the atmospheric reflected temperature obtained from the standard reflector test procedure. Aluminum foils and AL markers also help to locate regions of interest on the thermal images during post-processing.
The post-calibrated and optimized object parameters finalized in FLIR Thermal Studio are presented in
Table 3. Once these object parameters were finalized and inputted into the FLIR Thermal Studio tool, the LST for the ROI locations were readily obtained. Then, the LSTs were used to calculate the diurnal LST amplitudes.
2.6.2. Diurnal LST Data Modeling for Soil Moisture Content Characterization
The diurnal LST difference is calculated by taking the temperature difference between peak temperature and low temperatures within the day. Diurnal LST difference is inversely related to the soil moisture content [
31]. This underlying relationship was used to develop a regression model to estimate θ.
LST verification and diurnal temp range: Maximum LST was taken during midday peak temperatures. The temperature verification passed, as the TIR measured matched the soil probe temperature. LST min at dawn did not agree with the probe after the initial object parameter setup. The high relative humidity causes radiation scattering and impacts sensors’ accuracy in reading the radiation. To accommodate this scatter, TIR object parameters were adjusted. An emission of 0.82 brought LST closer to the probe temperature. Therefore, the emissivity of 0.82 was used for all images captured at dawn. LST was validated by comparing the pixel temperatures with the soil surface temperature measured using a probe thermometer. The comparison provided a good match, with a low Root Mean Square Error (RMSE) of 2.5, as shown in
Figure 11.
The typical dawn and midday thermal images next to their optical counterpart are presented in
Figure 12. The thermal images were optimized for better visualization by selecting the FLIR Thermal Studio’s inbuilt arctic color palette and temperature linear color distribution during post-processing.
4. Discussion
Soil moisture content variation has an undeniable influence on the stability of slopes [
1,
2,
3,
4,
5,
6], especially in the highway embankments of central Mississippi [
7,
40,
41,
42,
43]. Therefore, continual monitoring of soil moisture variation in highway slopes and embankments is imperative. This issue is even more relevant now because the adverse effects of climatological loading on aging infrastructure have become more pronounced in recent decades. One of the effective ways to adapt to these changes is to frequently monitor the performance of infrastructure assets and take preventative measures prior to failures. Therefore, this study aimed to develop innovative soil moisture monitoring methods using UAV images and machine learning methods to aid in the predictive maintenance of highway slopes and embankments prone to frequent shallow slide failures.
Inferencing soil moisture using remote sensing data and machine learning algorithms has been implemented in agricultural hydrology applications [
12,
16,
22,
23,
25]. However, these methods are rarely implemented for geotechnical infrastructure asset management. This study intended to fill the gap and develop near-surface soil moisture content prediction models using UAV images and machine learning methods.
Regression is the go-to method for forecasting or quantifying an underlying relationship between independent and dependent variables. The question is, “when is it prudent to use machine learning?” According to Chollet (2021) [
44], machine learning should be avoided when all the rules, data, and underlying relationships are known, but only target answers are needed. Instead, the problem can be solved by logical and mathematical reasoning. However, when data and target answers are known, but the rules are missing, a machine learning method is more suitable to solve the problem. Therefore, machine learning approaches were employed to develop RGB vs. θ models, as the underlying patterns are unclear. Specifically, Support Vector Regression (SVR), Extreme Gradient Boosting (XGB), and Multiple Linear Regression (MLR) methods were evaluated for θ inferencing using RGB data.
On the other hand, since there is an underlying relationship between the soil surface thermal inertia and the near-surface soil moisture content, singe parameter linear and power curve fitting models were tested to infer θ from LST. All optical and thermal imagery data used in this paper were collected and analyzed by the authors.
The XGB models’ performance metrics and the combination of parameters are presented in
Table 5. XGB1 and XGB2 show excellent R2 scores compared to XGB3. The Explained Variance Regression Score (EVS) function of the sklearn library close to 1 represents a healthy prediction model. EVS for all three XGB models were >0.9, proving good prediction quality. Additionally, the test dataset’s RMSE and MSE loss functions are close to zero, indicating well-performing models. Therefore, all three models are suitable for carrying out future predictions.
It is important to note that, although the SVR provided good results on the training dataset, the model failed to provide good predictions for the test dataset. Despite the good training results, the test results in terms of R2 score were poor. Furthermore, the test Explained Variance Regression Score (EVS) function is much farther from 1.0 and not indicative of healthy prediction models.
This paper is part of a more extensive study where the goal is to develop a methodology that can be adopted by transportation and engineering agencies to readily characterize and monitor soil properties, including soil moisture of highway embankments, through non-contact UAV surveys. Therefore, unaltered raw optical images in “as-is” status were used to extract RGB data. In future research, more parameters, including soil minerals, plant nutrition, and topography, can be incorporated to enhance nonlinear regression models for predicting the soil moisture content of geotechnical assets. This study can be expanded by including more datasets from different sites to eliminate bias from localized datasets. Furthermore, Multi-Level Perceptron (MLP or Neural Networks) and deep learning approaches can be explored to develop fusion models combining the color, thermal properties, and other parameters to predict soil moisture content from UAV images.
5. Conclusions
In this study, two different methods using UAV-captured optical and thermal images were developed to predict the near-surface soil moisture content of highway embankments in the Jackson, Mississippi, area. The first method used raw RGB color values from optical images to train machine learning models to infer θ. The second method used diurnal LST differences determined from thermal images to build regression models to estimate θ. The images were collected from three highway embankment sites in the Jackson, MS, metropolitan area. Bare Ground (BG), Vegetation Covered (VC), and mixed BG plus VC regions of interest were selected to collect ground truth soil moisture and extract RGB and land surface temperature values. Such multiclass ROIs were purposely selected to help generalize the θ inferencing capabilities of the developed models across both image classes.
This study conducted a literature review to identify frequently used machine learning models for predicting soil moisture content and compared their predictive performance to determine the best one. This comparative evaluation is necessary, as different models may perform differently depending on the problem and data. Three machine learning models were evaluated to predict soil moisture from RGB features. Extreme Gradient Boosting (XGB), Support Vector Regression (SVR), and Multiple Linear Regression (MLR) models were developed using ground truth soil moisture content as target and RGB pixel values as input features. The models were trained to predict θ from RGB values extracted from pixels belonging to Vegetation Covered (VC) and Bare Ground (BG) classes. The coefficient of determination, mean square error, and root mean square error metrics were used to evaluate the models’ performances. The results showed that XGB and MLR outperformed SVR models in predicting soil moisture content, with each having an R2 score of >0.9 for predicting soil moisture. A smaller RMSE value indicates better performance of the model. In this case, the RMSE values for XGB, SVR, and MLR were 0.009, 0.025, and 0.01, respectively, for the test dataset, thus proving that the XGB model’s performance was the best among the three models evaluated, followed by MLR. The XGB and MLR models were further validated by predicting soil moisture using previously unseen input data.
On the other hand, a power curve fit model was developed to predict the soil moisture content from thermal images. Radiometric data were first captured using a UAV-mounted FLIR Zenmuse-XT2 thermal sensor. After applying proper calibration, tuning, and validation steps, the land surface temperatures were extracted from the thermal images. A linear regression model was developed to predict θ from the diurnal variation of land surface temperature. The thermal inertia-based soil moisture prediction model (θ = 0.2794(ΔLST)−0.11) provided better results for vegetation-covered ROIs than the bare-ground ROIs, with a coefficient of determination of 0.748.
The results of this study are promising and present an innovative, time-efficient, and non-contact method to monitor soil moisture variations within the shallow depths of highway embankments. Transportation and engineering agencies can adopt this methodology into geotechnical infrastructure asset management and predictive maintenance programs.