GNSS Carrier-Phase Multipath Modeling and Correction: A Review and Prospect of Data Processing Methods

Abstract

A multipath error is one of the main sources of GNSS positioning errors. It cannot be eliminated by forming double-difference and other methods, and it has become an issue in GNSS positioning error processing, because it is mainly related to the surrounding environment of the station. To address multipath errors, three main mitigation strategies are employed: site selection, hardware enhancements, and data processing. Among these, data processing methods have been a focal point of research due to their cost-effectiveness, impressive performance, and widespread applicability. This paper focuses on the review of data processing mitigation methods for GNSS carrier-phase multipath errors. The paper begins by elucidating the origins and mitigation strategies of multipath errors. Subsequently, it reviews the current research status pertaining to data processing methods using stochastic and functional models to counter multipath errors. The paper also provides an overview of filtering techniques for extracting multipath error models from coordinate sequences or observations. Additionally, it introduces the evolution and algorithmic workflow of sidereal filtering (SF) and multipath hemispherical mapping (MHM), from both coordinate and observation domain perspectives. Furthermore, the paper emphasizes the practical significance and research relevance of multipath error processing. It concludes by delineating future research directions in the realm of multipath error mitigation.

1. Introduction

Since the deployment of GPS in 1995 and the successful establishment of the BDS-3 global network in 2021, globally, global navigation satellite systems (GNSSs) are composed of four major satellite navigation systems, the global positioning system (GPS) of the USA, the global navigation satellite system (GLONASS) of Russia, the BeiDou navigation satellite system (BDS) of China, and the Galileo satellite navigation system (Galileo) of the European Union [1]. GNSSs offer users all-weather 3D coordinates and velocity and time information at any point on the Earth’s surface or in the near-Earth space [2]. It possesses notable advantages, such as high accuracy, robust real-time capabilities, and a broad spectrum of applications. In comparison to other positioning systems, BDS not only provides navigation positioning and timing services, but also provides regional message communication and global SMS communication, global search and rescue services, regional precise point positioning services, embedded satellite-based enhanced services, and space environment monitoring functions [3].

Leveraging its unique advantages, GNSS observation technology finds widespread application in deformation monitoring and user position navigation and positioning. The GNSS receiver captures both direct signals from the satellite and signals reflected from the surrounding environment. The superimposition of the reflected signals onto the direct signals introduces errors in the positioning results [4]. The resulting positioning error is termed multipath error. GNSS positioning involves various errors, including satellite ephemeris error, satellite clock error, multipath error, ionospheric delay, and tropospheric delay [5]. In short baseline relative positioning, double-difference observations can mitigate or eliminate the influence of various errors, such as satellite and receiver clock errors and ionosphere and tropospheric delay errors. However, multipath errors, being associated with the station’s surrounding environment, cannot be mitigated by double-difference methods [6]. Particularly in complex environments, like deep mountains, woods, canyons, slopes, lakes, and urban areas, the presence of unavoidable reflectors leads to the generation of numerous satellite reflection signals, causing significant multipath effects. At this time, the multipath error becomes the primary source of errors affecting the accuracy of GNSS data processing in deformation monitoring and navigation positioning.

GNSS multipath errors are categorized into two types: satellite-side multipath errors and station-side multipath errors. Satellite-side multipath errors refer to the measurement errors caused by the multipath effect, which is caused by the signal reflected by the satellite itself [7]. Station-side multipath errors mean that there are reflectors in the environment around the station, and the reflected signals enter the receiver antenna and interfere with the signals directly from the satellite, making the observed value deviate from the true value. Satellite-side multipath errors are systematic errors, which are related to satellite elevation and can be eliminated by the fitting modeling method [8]. Station-side multipath errors are related to the surrounding environment of the station, and the surrounding environment of the station is their direct cause. GNSS multipath errors are classified using observations into two types: pseudo-range multipath errors and carrier-phase multipath errors. Under line-of-sight conditions, for the coarse acquisition (C/A) code, the impact of the multipath may reach 10~20 m, and in the most serious case, it may be as high as 100 m. The maximum impact on the precise code can be about 10 m. Under line-of-sight conditions, theoretically, the maximum value of the carrier-phase measurement error caused by the multipath effect is 1/4 of the carrier wavelength [9]. Multipath errors significantly impact the positioning accuracy and reliability [10] and are the primary error in high-precision positioning [11]. Multipath error mitigation is of great significance for further improving GNSS positioning accuracy [12]. It has significant research implications in application fields, such as deformation monitoring and urban positioning, and is also a key and hot topic in the field of GNSS research [13].

At present, there are primarily three approaches for mitigating multipath errors. The first involves the strategic selection of a suitable station to avoid a large number of reflectors in the surrounding environment of the station. The second method entails enhancing hardware components, including antennas and receivers, to inhibit the ingress of reflected signals into the antenna and suppress multipath effects during the receiver signal processing stage. The third method involves post-processing data, encompassing techniques such as the signal-to-noise ratio method, sidereal filtering (SF), and multipath hemispherical map (MHM). Despite the merits associated with these methods, they are not without limitations. Notably, sidereal filtering and the hemispherical multipath map exploit the repetitive characteristics of multipath errors in both the time and spatial domains, demonstrating effectiveness in mitigating multipath errors. These are recent common methods and are also research hotspots.

This paper predominantly focuses on the carrier-phase multipath error occurring at the station side in GNSSs. In Section 2, its principle and mitigation methods are explained. In Section 3, an overview of its research status is provided, with a focus on the commonly employed software methods, such as the sidereal filtering method and the multipath hemispherical map model method. In Section 4, the practical significance of mitigating the multipath effect in different application scenarios is discussed. Finally, Section 5 offers a prospective outlook on the future research directions in GNSS multipath research.

2. Multipath Error Principle and Mitigation Methods

2.1. Generation Principle of Multipath Errors

During the propagation process of the GNSS satellite signal from the satellite to the receiver, the signal reflected by the reflector enters the receiver and interferes with the direct signal, causing the time and phase delays of the satellite signal, making the GNSS observation value deviate from the true value. The interference delay effect caused by the superposition and propagation of satellite signals from different paths is called multipath effect, and the deviation of the GNSS observation value caused by it is called multipath error. There are multipath effects from both the satellite side and the station side. The satellite-side pseudo-range multipath error mostly occurs in BeiDou inclined geosynchronous orbit (IGSO) and middle earth orbit (MEO) satellite pseudo-range observations, and is related to the satellite elevation and belongs to a special systematic error, which is not discussed in this article. The multipath error from the station side is affected by the surrounding environment of the station and cannot be eliminated using the double-difference method. Figure 1a is a schematic diagram of the multipath effect of horizontal ground signal reflection and Figure 1b is a schematic diagram of the multipath effect of vertical building signal reflection.

There is a phase delay θ between the reflected wave and the direct wave. In the case of horizontal ground signal reflection, θ can be expressed as:

$$\theta =\frac{4\mathsf{\pi }H\sin z}{\lambda }$$

(1)

where H is the height from the antenna to the ground, λ is the carrier wavelength, and z is the incident angle of the reflected signal.

In the case of vertical building signal reflection, θ can be expressed as:

$$\theta =\frac{4\mathsf{\pi }L\cos z}{\lambda }$$

(2)

where L is the horizontal distance between the antenna and the building reflector.

The multipath error in the carrier-phase measurement can be expressed as [14]:

$$\phi =\frac{\lambda }{2\mathsf{\pi }}\arctan \frac{\alpha \sin \theta }{1+\alpha \cos \theta }$$

(3)

where α is the reflection coefficient of the reflector.

According to the above formula, the size of the multipath error is affected by factors such as the reflection coefficient of the reflector, the incident angle of the reflected signal, and the spatial relationship between the reflector and the receiver. Since satellite signals are reflected by water bodies, trees, slopes, buildings, and other reflectors, the reflection coefficients are different, resulting in different multipath effects. The theoretical upper limit of the multipath error, denoted as φ, is interconnected with α. In the case of horizontal ground reflection signals, when the incident angle and its rate of change are constant, the frequency of the multipath error is positively correlated with the receiver instrument height. In the case of vertical building reflection signals, when the incident angle and its rate of change are constant, the frequency of multipath errors is positively correlated with the horizontal distance from the instrument to the building. The multipath errors produced by carrier signals of different wavelengths are also different.

Under conditions where the station receiver’s position and its surrounding environment remain stable, with unaltered reflection coefficients and positional relationships between the reflector and the receiver, the incident angle of the reflected signal undergoes regular changes due to the periodic movement of the satellite in a fixed orbit. Due to the periodic repeatability of the GNSS satellite orbital motion, multipath errors have repetitive characteristics in the time domain and spatial domain. Two methods for mitigating multipath errors, namely, sidereal filtering and the multipath hemispherical map, leverage the repeating characteristics of multipath errors.

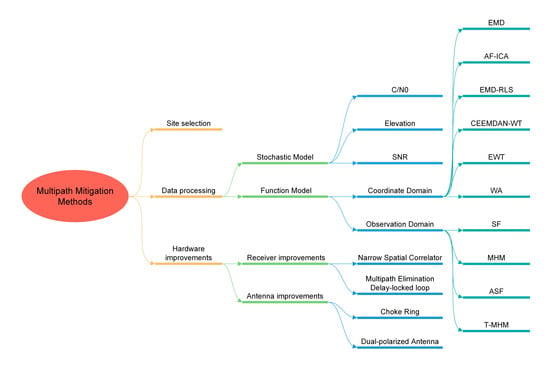
2.2. Multipath Error Mitigation Methods

The research on multipath error mitigation methods from the station side should be distinguished between occurrences in a line-of-sight (LOS) environment and a non-line-of-sight (NLOS) environment. This paper primarily elucidates the approach to mitigating carrier-phase multipath errors from the station side in a line-of-sight environment.

At present, multipath error mitigation methods can be broadly categorized into three groups: site selection, methods based on hardware improvement, and methods based on software data processing. Site selection involves opting for an open and suitable geographical location to set up a GNSS receiver [15]. The presence of water bodies with high reflection coefficients can significantly impact the multipath error when they surround the station. When there is a large water body around the station, it seriously affects the multipath error. The reflection coefficient of ground vegetation, such as grassland, is low, the reflection signal is weak, and the multipath error generated is small. The antenna suppression plate in the receiver can block most of the reflected signals from the horizontal ground, but when there are high-rise buildings or high-terrain environments around the station, the satellite signal is reflected by the vertical surface and enters the receiver, causing multipath errors. When the measuring station is set on a hillside and the slope is large, it affects the receiver’s reception of satellite signals and produces multipath effects. In station selection, it is advisable to avoid surroundings with high reflection coefficients, such as water bodies and glass, and to steer clear of challenging terrains, like slopes, valleys, and urban canyons. While a judicious site selection can diminish the impact of multipath effects [16], it is subject to relatively significant limitations.

The method of mitigating multipath errors through hardware enhancements encompasses two primary aspects: the antenna method and the receiver method. The antenna method is mainly used to improve the antenna in order to suppress the multipath effect. GNSS signals are right-handed circularly polarized signals, but most of the reflected signals are left-handed circularly polarized signals. The GNSS antenna is designed as a right-handed circularly polarized receiving antenna, which can effectively suppress the reflected signal, because the gain of the incident right-handed circularly polarized signal is larger than that of the left-handed circularly polarized signal [17]. Filippov et al. [18] proposed a choke ring technology for GPS dual-frequency signals in 1998, which can optimize L1 and L2 frequency signals. Ray et al. [19] suppressed low- or negative-altitude signals by adding choke rings. Krantz et al. [20] proposed a new antenna technique using a compression wheel to control the receive pattern in order to reduce multipath effects in GNSS signals. Danskin et al. [21] proposed a choke ring. Groves et al. [22] proposed a dual-polarized antenna technique using the polarization characteristics of GNSS original and reflected signals. Maqsood et al. [23] proposed compact cross-plate reflection planes with a low multipath effect. Zhang et al. [24] proposed a single orthogonal dual linearly polarized GNSS technology to suppress multipath effects through dual linearly polarized antennas. The multipath suppression method based on the antenna technology has a poor multipath suppression effect on low-altitude observation satellites. The receiver method is mainly used to improve the receiver in order to suppress the multipath effect. Nee [25] proposed a multipath elimination delay-locked loop technology to identify and suppress multipath signals in the carrier-phase-locked stage, thereby improving the accuracy of original observations. Chen et al. [26] proposed an improved group-delay multiple amplitude phase-locked loop technology to further improve the multipath suppression effect at the receiver. Dieredonck et al. [27] proposed a narrow spatial correlator technique to suppress multipath effects from the perspective of the receiver hardware. By improving the hardware of the receiver, the effect of alleviating the multipath effect in the middle- and long-band delays is better, but it cannot effectively weaken the impact of the short-band delay. Qiu et al. [28] proposed a multipath mitigation algorithm based on the steepest descent method and designed a new ranging code tracking loop, which has the advantages of a lower computational load and does not require external assistance. This algorithm is computationally more efficient than narrow-pitch correlation techniques.

Table 1. A summary of hardware methods.

Type	Method	Year	Scholar
Antenna method	Choke ring technology	1998	Filippov [18]
	Compression wheel antenna technology	2001	Krantz [20]
	Dual-polarized antenna technique	2010	Groves [22]
	Cross-plate reflection planes	2013	Maqsood [23]
	Single orthogonal dual-polarized GNSS antenna	2017	Zhang [24]
Receiver method	Narrow spatial correlator technique	1992	Dieredonck [27]
	Multipath elimination delay-locked loop technology	2002	Nee [25]
	Group-delay multiple amplitude phase-locked loop technology	2013	Chen [26]
	New ranging code tracking loop	2022	Qiu [28]

summarizes multipath mitigation methods based on the antenna and receiver. By improving the antenna and receiver, the reflected multipath signal from the surrounding environment cannot be completely shielded, and the suppression effect on the multipath effect is limited.

The approach to mitigating multipath errors through software data processing encompasses four key aspects. The first aspect is the multipath suppression method based on a stochastic model. In the second aspect, to leverage the frequency domain characteristics of multipath errors, filtering methods such as Vondrak filtering, empirical mode decomposition (EMD), and wavelet analysis are employed to extract the multipath error time series. These time series are then used to establish a multipath error correction model for post-processing correction. In the third aspect, based on the time domain repetition characteristics of multipath errors, time domain multipath error modeling methods based on the coordinate domain and the observation value domain are developed. The principal methods include sidereal filtering and advanced sidereal filtering (ASF). The fourth aspect is the modeling method based on the repeatability of the multipath spatial domain. The main methods include the multipath spherical harmonic model, multipath stacking (MPS), and multipath hemispherical map. In a static environment, based on the time-spatial domain repetition characteristics of multipath errors, sidereal filtering and hemisphere map model can generate a multipath correction model for real-time GNSS data processing.

3. Research Status of the Multipath Error Data Processing Algorithm

In GNSS relative positioning, the carrier-phase multipath error at the station end is intricately linked to the surrounding environment of the station, which cannot be eliminated by the double-difference method, and is the main source of the errors affecting the positioning results. Consequently, addressing the carrier-phase multipath errors from the station side remains a challenging and focal point in the field of GNSS positioning error processing. Since the 1990s, scholars globally have been engaged in research aimed at mitigating carrier-phase multipath errors, approaching the issue from various perspectives. Numerous multipath error correction methods, based on software data processing, have been proposed as a result of these endeavors. These correction methods can be categorized into two groups based on different research perspectives: mitigation methods based on the stochastic model and mitigation methods based on the function model.

3.1. Multipath Error Mitigation Methods Based on the Stochastic Model

A stochastic model that reasonably weighs observations through the satellite’s elevation, signal to noise ratio (SNR), and carrier-to-noise power density ratio (C/N0) can mitigate multipath errors and improve the positioning results. C/N0 reflects the quality of GNSS observations. Brunner et al. [29], based on the SIGMA-Δ stochastic model using the measured C/N0, demonstrated the ability of the SIGMA-Δ model to reduce signal diffraction effects on static GPS measurements and high-precision GPS railway measurements. This method improves the accuracy of GPS results by more than 50% over the standard GPS processing techniques. According to the correlation between the SNR and multipath effects, the oscillatory variation in the SNR can reflect the influence of the multipath effect. Reducing the weight or identifying and eliminating poor observation data can reduce the impact of multipath effects. Zhang et al. [30] used the signal to noise ratio as an evaluation index and verified through experimental data that reducing the weight of the observations affected by multipath effects can mitigate multipath errors. Liu and Dick [31] constructed a GPS-refined stochastic model using the correspondence between the variance in GPS observations and the signal to noise ratio. The measured data showed that the accuracy of baseline processing can be improved, which verifies the validity and necessity of GPS stochastic model refinement. GNSS observations with higher elevations are more precise. Ding [32] added three models based on satellite elevation, signal to noise ratio, and least-squares residual error to the high-precision IGS station baseline vector calculation to improve the calculation accuracy. Strode and Groves [33] developed a multipath detector based on the signal to noise ratio of three frequencies, detected GNSS multipath errors by comparing the signal to noise ratio measurements of the three frequencies, and tested and verified its multipath detection capability in an urban environment. Zhang et al. [34] proposed a real-time adaptive weighting model based on satellite elevation and C/N0, which can reduce multipath errors, and applied it to simplified parallel process (SPP) and real-time differential (RTD). The test results showed that the adaptive model was better than the equal weight model, elevation model, and C/N0 model. Zhang [35] proposed a real-time multipath detection method using dual-frequency C/N0, which improves the reliability of multipath detection. Xi et al. [36] analyzed the SNR characteristics of GPS and GLONASS, proposed an improved stochastic model based on the SNR, and reasonably established the link between carrier-phase accuracy and SNR observations. The improved model can be used in real time and can reasonably display carrier-phase accuracy with signal-to-noise ratio data, which is applicable to all GNSSs. Liu et al. [37] proposed a multipath error identification method for GNSS observation data based on the prior information of the signal to noise ratio of reference stations. Satellite signal to noise ratio observations have a strong correlation with multipath errors. Poor data that are seriously affected by multipath effects can be identified by the inter-station difference of SNR observations, and they are eliminated to resist the multipath effects’ influence on monitoring complex environments.

The equal-weight model assumes uniform accuracy for each observation, overlooking the impact of errors such as elevation and multipath effects on observation accuracy and deviating from the real conditions. Stochastic models that use elevation, SNR, or C/N0 to determine the weight are more in line with the actual situation and reflect the quality and precision of the observations. Some popular stochastic models are presented in

Table 2. A summary of stochastic models.

Model Type	Contributions	Year	Scholar
C/N0	Construction of the SIGMA-Δ model based on C/N0	1999	Brunner [29]
	dual-frequency C/N0	2019	Zhang [35]
SNR	Validation of the effectiveness of the SNR method to	2003	Zhang [30]
	refine a stochastic model for GPS	2003	Liu [31]
Elevation	Refined stochastic model for multi-GNSS	2020	Xi [36]
	real-time adaptive weighting model	2018	Zhang [34]

.

3.2. Multipath Error Mitigation Method Based on the Function Model

The multipath mitigation method based on the function model refers to the construction of the corresponding multipath error correction model by using the physical or geometric relationship between the observation value or coordinate value in the GNSS data and the multipath error. Based on the time domain repetition characteristics of multipath errors, the time domain multipath error modeling method using the calculated satellite orbit repeat period is called sidereal filtering (SF). Another classic modeling method based on the repeatability of the multipath spatial domain is the multipath hemisphere map (MHM). Genrich and Bock [38] first proposed sidereal filtering, using the satellite orbit repeat period, and established a multipath error correction model by calculating the satellite repeat period. Choi et al. [39] studied the repeat period of the GPS orbit and found that the repeat period is different for each satellite. Agnew and Larson et al. [40] used the orbital period and the topological center position of the satellite to calculate the repetition time and found that the repeat period of the satellite constellation is variable. Modified sidereal filtering (MSF) uses the average of the orbital repetition times of all satellites as the multipath repetition time. However, due to differences in satellite repeat periods, individual multipath modeling for each satellite is most efficient, called advanced sidereal filtering (ASF). Sidereal filtering has been applied to the coordinate domain and the observation domain. The multipath error is extracted from the previous coordinate sequence by the filtering method, and the multipath error of the coordinate sequence in the next cycle is corrected according to the calculated repeat period to obtain the corrected coordinate sequence. This coordinate domain-based sidereal filtering is suitable only for data post-processing and cannot correct multipath errors in real time. The time domain multipath model in the observation domain utilizes the correlation of the observation residuals in the satellite orbit repeat period and extracts the multipath error components in the observation residuals through the time series analysis method to achieve multipath error correction for observations in the next satellite orbit repeat period [41], which corresponds to the sidereal filtering method based on the observation domain.

Sidereal filtering (SF) exerts a substantial impact on mitigating multipath errors in static environments. However, it proves unsuitable for dynamic scenes as it necessitates the advance calculation of the satellite repeat period, involving extensive modeling and intricate calculations. Compared with the coordinate domain, SF in the observation domain is more suitable for BDS containing three orbit types. MHM can significantly weaken the multipath error in the observation domain, and can be applied to precise point positioning and dynamic scenes, where the surrounding scenes remain unchanged. MHM is particularly adept at low-frequency multipath error correction rather than high-frequency multipath error correction. In addition, it is not well-suited for conventional receivers.

3.2.1. Multipath Error Mitigation Method Based on the Coordinate Domain

The coordinate sequence of the previous repeat period is analyzed using the filtering method to extract the multipath error time series in the coordinate domain, and then the multipath error correction model is constructed. Based on the repetitive characteristic of multipath effects, multipath error correction is performed on the sequence of coordinates for the next repeat period. The GPS/BDS/GLONASS/Galileo repeat period can be observed in

Table 3. GPS/BDS/GLONASS/Galileo Repeat period.

	Orbit Type	Repeat Period
GPS	MEO	1 day
BDS	GEO	1 day
	IGGSO	1 day
	MEO	7 days
GLONASS	MEO	8 days
Galileo	MEO	10 days

. It is a key point to use various filtering methods to denoise and isolate the multipath correction model with repeatability. Such methods can only be used for data post-processing. Zheng et al. [42] proposed a data filtering method called cross-validation Vondrak filter (CVVF) based on the Vondrak filter and cross-validation technology, which is used for signal and noise separation in data sequences and is applied to mitigate GPS multipath effects for deformation monitoring. Dai et al. [43] established a new denoising filtering method based on empirical mode decomposition (EMD) and applied this method to GPS multipath error correction. EMD entails the separation of several basic signals from complex signals, from high frequency to low frequency, and the separated signal is called the intrinsic mode function (IMF). For a signal mixed with random noise, the decomposed high-frequency IMF components are usually the noise of the signal and the low-frequency components are multipath signals. However, EMD presents problems that need to be addressed. Xue and Luo proposed two methods based on EMD improvements, ensemble empirical mode decomposition (EEMD) [44] and complete ensemble empirical mode decomposition (CEEMD) [45], to filter and denoise the signal. EEMD and CEEMD are able to mitigate the modal aliasing problem in EMD. Tong [46] proposed a method for extracting GPS/BDS-3 multipath errors based on complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN)-wavelet transform (WT). The positioning results of this method were better than those of EEMD and CEEMD. Chen et al. [47] used the IMF obtained by EMD as the input and applied the generalized eigenvalue decomposition (GED) blind source separation algorithm to extract the multipath error model of the repeat period. Yan et al. [48] first used EMD to decompose the original signal to obtain three IMFs, and then used the recursive least-squares algorithm (RLS) to filter the mixed IMFs. The obtained new IMF and information IMF were reconstructed to extract the multipath error correction model. Singular spectrum analysis is an effective method for extracting information from short noise time series. Lu et al. [49] proposed a new SSA filtering method based on the significant difference between noise and signal Hurst exponents, and verified its effectiveness using GPS data. Zhong et al. [50] proposed a wavelet signal-layer automatic identification method based on cross-validation technology, which can separate the noise whose amplitude level is lower than about half of the signal amplitude, and applied it to the mitigation of GPS multipath effects. The repeatability of multipath effects is the highest for two consecutive periods; however, repeatability decreases as the time between the first period and subsequent periods increases. In order to solve this problem, Dai et al. [51] developed a combined method of principal component analysis and empirical mode decomposition and independent component analysis with reference (PCA-EMD-ICA-R), which analyzes the coordinate time series of the first period to obtain the reference multipath model for the second period and has a significant multipath error mitigation effect in both static and dynamic environments. Luo et al. [52] combined the advantages of the empirical wavelet transform (EWT) algorithm in decomposing complex signals with the diurnal repetition characteristics of GNSS multipath errors, and proposed a new method for extracting and correcting multipath errors based on EWT. Zhang et al. [53] used the height of the high-speed rail track as a constraint to solve GPS data, and then analyzed the coordinate sequence with wavelet, which weakened the multipath error of rail train positioning in a dynamic environment. Cao et al. [54] compared and analyzed the ability of two least-squares harmonic estimation methods, unit harmonic estimation and multi-harmonic estimation, to extract multipath errors in the coordinate domain. Yuan et al. [55] proposed an adaptive fast independent component analysis (AF-ICA) method, which can effectively separate and weaken multipath signals when applied to GNSS deformation monitoring.

The algorithm flow of the sidereal filtering method based on the coordinate domain to weaken the multipath error is shown in Figure 2. Firstly, the GNSS baseline monitoring data of the first period is solved to obtain the coordinate solution of the corresponding station. The first-period data are pre-processed, and BDS MEO satellites are not considered in the case of GPS/BDS fusion positioning. Then, filter processing, such as wavelet analysis, is performed to extract the low-frequency components of the data, so as to obtain the periodic error sequence related to the multipath effect. Then, the calculated average repeat period is used to obtain the multipath error correction model based on SF. This model is used to correct the coordinate data of the second period epoch by epoch, and finally, the coordinates after multipath error correction are obtained.

3.2.2. Multipath Error Mitigation Method Based on the Observation Domain

The multipath error is related to the geometric relationship among the measuring station, the reflector, and the satellite position. In a static environment, the multipath error presents a repeating regularity in time domain and spatial domain as the position of the satellite moves [56]. In an unobstructed observation environment, the satellite single-difference residual sequence theoretically presents the characteristics of white noise and is related to the satellite elevation. The satellite single-difference residual sequence under the influence of the multipath effect presents a low-frequency fluctuation trend, and the low-frequency component is the observation domain error caused by the multipath effect. There is a strong correlation between the low-frequency components of different satellite repeat periods. The achievement of multipath error correction in the time domain is divided into three steps: extracting the low-frequency component of the single-difference residual of each satellite; calculating the time offset of the satellite repeat period; and correcting the observations in the next satellite repeat period. Zhong et al. [57] proposed an algorithm to convert double-difference residuals to single-difference residuals based on the “zero-mean assumption”. By establishing a reference period single-difference multipath model for each satellite, and using the periodicity of multipath errors, multipath error correction is performed on the observations in the following periods. v experimental results showed that the method is applicable to different GPS satellites and can effectively correct long-period and short-period multipath errors. Wang et al. [58] proposed three methods for calculating satellite repetition shift times, which are the broadcast ephemeris method (BEM), the correlation coefficient method (CCM), and the aspect repetition time method (ARTM). Wang et al. [59] compared the performance of ASF with modified sidereal filtering (MSF) to evaluate the ability to weaken the multipath error, and the performance of ASF was slightly higher than that of MSF. Li et al. [60] discussed how to model multipath errors in the observed range and evaluated the accuracy of the model algorithm using real-time deformation monitoring data. In order to accurately estimate the repeat period of multipath errors, Zhan et al. [61] proposed a real-time window matching method, combined with SF, to achieve near real-time positioning.

In order to achieve the extraction of the low-frequency component of the satellite single-difference residual under the influence of multipath effects, where single difference refers to the between-station difference of the carrier-phase measurements for the same satellite, it is necessary to use the filtering method. The classical methods include wavelet analysis, EMD, and the Vondrak filter. Satirapod and Rizos [62] applied wavelet decomposition to GPS double-difference residuals to extract GPS carrier-phase multipath errors. This multipath error component was then removed directly from the GPS carrier-phase observations in subsequent days of observation data. El-Ghazouly [63] conducted a comprehensive evaluation of different wavelet techniques that can be used to attenuate multipath errors and proposed a new method based on the wavelet detrending technique to attenuate carrier-phase multipath errors in the observation domain. Yuan et al. [64] proposed a new unscented Kalman filter (UKF) to estimate the multipath parameters of weak GPS signals. The simulation results demonstrated the effectiveness of the method for estimating the multipath parameters of weak GPS signals with a carrier-to-noise ratio as low as 21 dB-Hz. Zhang et al. [65] used the Kalman filter (KF) and Rauch–Tung–Striebel smoother (RTSS) to extract multipath error sequences from the single-difference residuals of observations and compared it with the wavelet technique and EMD. The experimental results showed that the performance of KF-RTSS was better than that of the wavelet technique and EMD. Lau and Lawrence [66] proposed a general and robust three-stage wavelet denoising method for repetitive time-based carrier-phase multipath filtering in relative positioning. Su et al. [67] used the satellite elevation as the constraint information of the wavelet transform to extract an accurate multipath error model and then used SF for multipath error correction.

The space part of the BDS system consists of GEO, IGSO, and MEO to form a hybrid heterogeneous constellation. There are many high-orbit satellites in BDS that have a strong anti-blocking ability. Due to the unique constellation design of BDS, many scholars have found that the multipath effect characteristics of BDS satellites are significantly different from those of other systems; thus, considerable research has been conducted. Wu et al. [68] proposed a real-time multipath correction algorithm for IGSO and GEO satellites, called code noise and multipath correction (CNMC), which reduces the influence of multipath errors, thus ensuring the performance of the system. Ye et al. [69] applied the sidereal filtering method based on the observation domain to BDS and considered the repeat period of each satellite independently, successfully weakening the BDS carrier-phase multipath error. The results showed that the combined system of GPS and BDS has a higher reliability and higher accuracy than a single system. Ye et al. [70] analyzed the ambiguity fixation rate of BDS and GPS in different resolution modes and weakened the influence of wide-lane multipath effects through the sidereal filtering method in the observation domain. Shi et al. [71] analyzed the multipath repeatability of three types of BeiDou satellites in different orbits by calculating the residual sequence of double-difference observations, and on this basis, studied the influence of multipath effects on the accuracy of the BDS static baseline solution. The results showed that, in a strong multipath environment, the impact of BDS multipath errors on its static solution reaches the centimeter level. Xie et al. [72] used SF based on the coordinate domain to weaken the multipath error of the BeiDou satellite deformation monitoring data, which effectively improved the accuracy of the plane and elevation directions. Based on single-difference residual reconstruction and wavelet decomposition, Yang et al. [73] proposed a BDS system multipath mitigation method combining sidereal filtering and wavelet. Zhang et al. [74] showed that, in the relative positioning of the BDS-2 and BDS-3 systems, MHM can effectively correct the multipath error of low-elevation satellites and improve the success rate of ambiguity resolution, and the positioning accuracy of the floating-point solution and the fixed-point solution can be improved.

The Galileo satellite orbit repeat period is ten days, and the existing SF and MHM need a large amount of data for modeling when dealing with Galileo multipath errors, which is not applicable. The elevation and azimuth between adjacent epochs do not change considerably; thus, it can be considered that the low-frequency phase multipath effect at adjacent epochs is unchanging. Based on this, Hu et al. [75] proposed a random walk multipath method (RWM), which can alleviate Galileo multipath errors and improve the localization accuracy without using historical data. Tian et al. [76] proposed a least-squares collocation (LSC) method based on the covariance function, which can effectively weaken the multipath error when applied to the baseline positioning and precise single-point positioning of GPS and Galileo (Tian and Liu et al. (2023)). This method has a higher modeling efficiency in the Galileo system.

Ragheb et al. [77] compared the sidereal filtering method based on the coordinate domain and the observation domain, and the results showed that the accuracy of the observation domain was slightly higher than that of the coordinate domain, but the calculation efficiency of the coordinate domain was higher, and the processing time of the observation value domain was longer. When using the sidereal filtering method based on the coordinate domain to reduce the multipath effect, the coordinates are obtained from different satellite solutions. The coordinates are mixed with the influence of different satellite signals on the coordinate data. Especially when different constellations are used for multi-system joint positioning, the repeat period of different satellites is very different, which is not conducive to weakening the multipath error. Therefore, multipath modeling should be performed on each system satellite separately in the observation domain. Compared with the two methods, the sidereal filtering based on the observation domain can take into account the multipath error repeat period of each satellite and is more suitable for the reduction in multipath errors of BDS with heterogeneous constellations.

The multipath error correction of SF based on the observation domain is divided into two aspects. Firstly, the SF multipath model is constructed based on the first-phase GNSS observation data; then, the SF model is used to perform multipath error correction on the second-phase GNSS observation data. The algorithm flow of the SF multipath model to correct the multipath error is shown in Figure 3. The algorithm includes the following six steps:

• According to the first phase of GNSS navigation ephemeris data, the average angular velocity of different satellites is calculated and the time offset of the repeat period of different satellites is obtained.
• According to the GNSS baseline observation data of the first phase, errors such as satellite clock error, receiver clock error, satellite orbit error, tropospheric delay, and ionospheric delay are eliminated by constructing a double-difference observation equation. The double-difference ambiguity is fixed using the LAMBDA algorithm.
• Double-difference residuals are converted to single-difference residuals based on the “zero-mean assumption”; wavelet analysis, EMD, or other filters are used to process the signal, and low-frequency components of single-difference residuals are extracted.
• Using the obtained satellite repetition cycle time offset, the satellite single-difference residual time series is time-corrected based on GPST to obtain the single-difference residual low-frequency component correction model for the next repetition cycle. Finally, the SF model of the observation domain for multipath error mitigation in the next period is obtained.
• According to the GNSS baseline observation data of the second phase, the satellite single-difference observation equation is constructed, and the corresponding satellite multipath error correction value in the sidereal filtering multipath model is extracted based on the GPST timestamp. The single-difference observation equation weakened by the multipath error is reconstructed into a satellite double-difference observation equation.
• The Kalman filter is used to estimate the floating-point solution of the ambiguity, and the LAMBDA algorithm is used to fix the double-difference ambiguity. The double-difference ambiguity is substituted into the solution equation to obtain a fixed-point solution for the baseline solution, which mitigated the multipath error.

The geometric relationship between the satellite and the station is used to model and correct the multipath error. The modeling methods based on the repeatability of the multipath spatial domain mainly include the multipath spherical harmonic model, multipath stacking (MPS), and MHM. Based on the principle of superposition, Cohen and Parkinson [78] used spherical harmonics as a calibration function and applied this calibration model to GPS measurements to weaken multipath errors. Fuhrmann et al. [79] proposed MPS that considers geometric and statistical aspects, is able to detect far-field and near-field multipath signals, can be used in real time and for post-processing, and is applicable to all satellite systems.

When the observation environment remains basically unchanged, the change characteristics of the single-difference residual of the satellite carrier observation value are related to the azimuth and elevation, and the change characteristics are consistent in the spatial domain. The single-difference residuals of the carrier observations in different satellites and the different frequencies of the same satellite have different variation characteristics. The MHM model with the receiver as the origin, the elevation as the latitude, and the azimuth as the longitude for grid division can express satellite single-difference residual spatially varying characteristics. Based on the single-receiver multi-antenna hardware and unified time system, Dong et al. [80] directly constructed a single-difference observation equation, taking into account the altitude angle and azimuth angle of each satellite, and established the MHM model suitable for real-time deformation monitoring, which significantly mitigated the impact of multipath errors. Cai et al. [81] extended MHM to the kinematic shipboard environment, conducted static and kinematic tests, and proved the feasibility of MHM. On the basis of MHM, Wang et al. [82] proposed an MHM model based on the trend surface analysis method, called T-MHM, focusing on the correlation of multipath errors in the satellite spatial domain, which effectively mitigated multipath errors. In the baseline E, N, and U directions, T-MHM has a higher positioning accuracy than MHM. To solve the problem of the multicollinearity and overfitting of the fitting parameters in the T-MHM, Wang et al. [83] proposed the AT-MHM method. Theoretically, this method can be applied to carrier-phase multipath error correction. Aiming to obtain the multipath error characteristics of satellites with different elevation values, Zheng et al. [84] proposed an improved MHM, which reduces the influence of multipath errors on precise point positioning under static conditions. Wang et al. [85] proposed a multi-point hemispherical grid model (MHGM) to directly model the double-difference residual, which can be applied to common receiver hardware equipment. Zhang et al. [86] presented the MHM_V model based on variational mode decomposition (VMD) and MHM. They using the VMD algorithm to extract multipath errors from the single-difference residuals and to correct the original observations of the carrier phase within a few days after implementation according to the principle of recent elevation and azimuth angles to mitigate multipath effects. Tang and Liang [87] used ensemble empirical mode decomposition (EEMD) to accurately extract the multipath errors in the observation domain and combined with the MHM model to correct the multipath errors in real time, indicating the importance of the accurate extraction of multipath errors. The development of the MHM method is presented in

Table 4. A summary of MHM models.

Method	Scenario	System	Year	Scholar
Multipath spherical harmonic model	Baseline positioning	GPS	1991	Cohen [78]
MPS	PPP	GNSS	2015	Fuhrmann [79]
MHM	Baseline positioning	GNSS	2016	Dong [80]
T-MHM	Baseline positioning, PPP	GNSS	2019	Wang [82]
M-MHM	PPP	GNSS	2019	Zheng [84]
MHGM	Baseline positioning	GPS	2020	Wang [85]
AT-MHM	Baseline positioning, PPP	GNSS	2020	Wang [83]

.

These methods are adaptable to multiple GNSS systems and can be applied to baseline positioning and precise point positioning. In a relatively constant observation environment, MHM can significantly mitigate multipath errors; thus, this type of model is of great value for evaluating multipath errors, and this is also one of the current research hotspots.

The multipath error correction of MHM is divided into three aspects. Firstly, the multipath error sequence of the GNSS observation data is extracted, and then the MHM model is constructed according to the elevation and azimuth. Finally, the obtained MHM model is used to correct the multipath error of the second-phase GNSS observation data.

The algorithm flow of the MHM model to correct the multipath error is shown in Figure 4, and the algorithm includes the following six steps:

• Single-difference residual low-frequency components are extracted using the filtering method from the first-period observation data.
• For different satellite constellations, different hemisphere geometric models are established. Based on the minimum elevation, maximum elevation, azimuth angle, minimum grid latitude, and minimum grid longitude, the hemispherical geometric model of GPS/BDS IGSO/BDS MEO satellites is established; based on the minimum elevation, maximum elevation, minimum azimuth, maximum azimuth, minimum latitude interval, and minimum longitude interval, the semi-celestial geometric model of the BDS GEO satellite is established.
• Based on the instantaneous elevation and azimuth of the satellite, the low-frequency components of the instantaneous single-difference residual of the satellite are divided into the corresponding grids of the hemispherical geometric model (HGM)/GEO hemispherical geometric model (GEOHGM).
• The mean value of the low-frequency component of the satellite single-difference residual in each grid is calculated, that is, the parameter fitting of the semi-celestial spherical grid. Finally the MHM/MHMGEO corresponding to HGM/HGMGEO is obtained.
• The second-phase GNSS baseline monitoring data are used to construct a single-difference observation equation. The grid parameters of the MHM model are obtained based on the satellite azimuth and elevation of the current epoch and the multipath error correction of the single-difference observation equation is conducted.
• The single-difference observation equation that was weakened by multipath errors was reconstructed into a satellite double-difference observation equation. The LAMBDA algorithm is used to fix the double-difference ambiguity and the double-difference ambiguity is substituted into the solution equation to obtain a fixed-point solution for the baseline solution.

3.2.3. Summary

The precise extraction of multipath models from coordinate sequences or observations is the most important step in multipath error data processing. This can be effectively achieved using filtering methods. According to the spatiotemporal repeatability of multipath errors, the core point of SF is the acquisition of the satellite orbit repeat period, and MHM focuses the fitting of the grid surface and the actual site multipath errors. In the utilization of SF in the coordinate domain, it is advisable to employ satellites with similar repetition periods. Notably, SF in the coordinate domain becomes impractical when dealing with satellites that have significantly divergent repeat periods, which represents a limitation. It can be observed in

Table 5. A summary of the popular multipath error mitigation methods.

Type	Method	Experimental Scene	System	Year	Scholar
Coordinate domain	CVVF	Baseline positioning	GPS	2005	Zheng [42]
	EMD	Baseline positioning	GPS	2006	Dai [43]
	Wavelet signal-layer automatic identification	Baseline positioning	GPS	2008	Zhong [50]
	EEMD	Baseline positioning	GPS	2012	Xue [44]
	PCA-EMD-ICA-R	Baseline positioning	GPS	2014	Dai [51]
	SSA	Baseline positioning	GPS	2015	Lu [49]
	CEEMD	Baseline positioning	GPS	2018	Luo [45]
	GED	Baseline positioning	BDS	2018	Chen [47]
	EMD-RLS	Baseline positioning	BDS	2019	Yan [48]
	EWT	Baseline positioning	GPS	2020	Luo [52]
	Wavelet analysis	Baseline positioning	GPS	2021	Zhang [53]
	Least-squares harmonic estimation	Baseline positioning	GNSS	2022	Cao [54]
	AF-ICA	Baseline positioning	GNSS	2022	Yuan [55]
	CEEMDAN-WT	Baseline positioning	GPS, BDS	2022	Tong [46]
Observation domain	Wavelet analysis	Baseline positioning	GPS	2005	Satirapod [62]
	Wavelet detrending technique	Baseline positioning	GPS	2009	El-Ghazouly [63]
	SF based on single differences	Baseline positioning	GNSS	2010	Zhong [57]
	Three-level wavelet packet-based denoising method	Baseline positioning	GPS	2017	Lau [66]
	KF-RTSS	Baseline positioning	BDS	2018	Zhang [65]
	MHM_V	Baseline positioning	GPS	2021	Zhang [86]
	MHM based on EEMD	Baseline positioning	GNSS	2022	Tang [87]
	SF based on EC wavelet packet transform	Baseline positioning	GNSS	2022	Su [67]
	SF-based sym6 wavelet decomposition	Baseline positioning	BDS	2022	Yang [73]
	Window-matching method based on SF	Baseline positioning	GPS, BDS	2022	Zhan [61]
	RWM	Baseline positioning	Galileo	2023	Hu [75]
	LSC	Baseline positioning, PPP	GPS, Galileo	2023	Tian [76]

that many filtering methods are used for multipath error correction. Taking into account the satellite constellation structure, the coordinate domain method is suitable for GPS with a simple structure, and the observation value domain method is more suitable for BDS with a complex structure. Most of the methods employ a combination of the filtering method and the SF or MHM models, which can effectively weaken the multipath error.

4. Application Scenarios of the Multipath Error Mitigation Algorithm

4.1. GNSS Deformation Monitoring

Since its development in the 1970s, the GNSS has become an indispensable part of space technology in the new century. With its advantages of high positioning accuracy, fast positioning speed, and precise timing [88], it has been applied in many disciplines, such as transportation, surveying and mapping, communications, deformation monitoring, precision agriculture, machinery control, and the monitoring and forecasting of geological hazards [89]. Since the 1990s, GNSS technology has been applied to deformation monitoring. Compared with traditional deformation monitoring, GNSS monitoring technology has unique advantages in large-scale structural health monitoring: high sampling rate, no need to supervise it, high degree of automation, four-dimensional monitoring, and all-weather monitoring [90]. GNSS monitoring technology can be applied to various monitoring scenarios to meet different monitoring requirements, such as monitoring types, monitoring accuracy, monitoring instruments, and monitoring range [91]. The GNSS deformation monitoring system is an important and effective way to obtain structure safety and health monitoring data. In the monitoring of specific projects, GNSS monitoring technology can obtain the high-precision deformation of structures, obtain vibration signals, and achieve the simultaneous monitoring of real-time and long-term deformation of structures [92]. With the development of global satellite navigation and positioning technology, multi-GNSS system data fusion processing has become a future development trend [93]. This evolution is expected to enhance the usability and reliability of GNSS deformation monitoring [94].

At present, GNSS monitoring technology has been widely used in monitoring fields such as high-rise buildings, dams, bridges, and building tailings. In terms of water dams, in 1995, Behr and Hudnut [95] developed the first GNSS dam non-real-time deformation monitoring system to monitor the deformation displacement of the Pacoima dam by continuously operating the GPS monitoring station system. The GNSS monitoring system can measure the horizontal and vertical displacements of water dams and surrounding adjacent areas, and can obtain centimeter-level or even millimeter-level deformation information [96]; it has also gradually become an important component of the dam safety and stability monitoring system [97]. High-rise buildings and large bridge structures are easily deformed or even damaged by external factors, such as wind, earthquakes, temperature, and vehicles [98]. Kwon et al. [99] established SmartSync, a rapidly deployable health and safety monitoring system at the Burj Khalifa, which accommodates multiple sensor types, including GPS, accelerometers, and weather stations, to monitor real-time deformation information of the Burj Khalifa in Dubai in order to ensure the structural health and safety of the entire structure. Ashkenazi et al. [100] applied GPS to the British Humber Bridge for monitoring experiments. The analysis of the verification test results showed that the GPS signal measurement results obtained very good experimental data, which is consistent with the finite element model analysis results. In terms of landslide monitoring, GNSS monitoring technology performs static calculations through satellite observation data over a period of time and obtains deformation and displacement information of landslide monitoring points within a corresponding period of time. Wang et al. [101] analyzed the reliability and accuracy of GPS technology applied to the dynamic real-time deformation monitoring of landslides by using large-scale physical model tests of landslides.

Obtaining accurate deformation information of the monitored object is the primary purpose of deformation monitoring. The existence of multipath errors seriously affects the data quality of monitoring points and reduces the availability of monitoring point positioning results [102]. When the error is serious, it causes the wrong deformation disaster warning of the monitored object [103]. Wang et al. [104] corrected the multipath error of the GPS data of the Foss Road Bridge through the single-difference sidereal filtering method, and the results showed that the positioning accuracy of the bridge deformation monitoring was greatly improved compared with the original results. Han et al. [105] used the sidereal filtering method to correct the multipath errors of GNSS landslide deformation monitoring data in the Qinba mountainous area and loess monitoring environment in real time, and the positioning residual accuracy was improved to the millimeter level. Chen et al. [106] considered that tropospheric errors and multipath errors exist simultaneously in long-baseline real-time kinematic (RTK) positioning, and corrected tropospheric errors and multipath errors successively by using the undifferenced residuals of satellites. This research provided an effective research strategy for long-baseline, high-precision, real-time dynamic carrier-phase difference technology RTK deformation monitoring. Liu et al. [107] used non-difference, single-difference, and double-difference sidereal filtering methods to process high-speed railway-based BeiDou satellite monitoring data, and the positioning accuracy in the three directions was effectively improved. The sidereal filtering method based on the single-difference procedure has the best effect on weakening the multipath error of high-speed railway foundation deformation monitoring. Tong et al. [108] proposed an empirical wavelet transform independent component analysis reference (EWT-ICA-R) method, which can accurately extract deformation information from GNSS coordinate sequences. The experimental results showed that the extraction of deformation information was expected to achieve submillimeter precision.

The multipath error exhibits a strong correlation with the receiver environment of the station. When monitoring the deformation of the structure, the buildings, water environment, and tree vegetation around the station cause multipath effects. The resultant multipath error, not amenable to elimination through the double-difference method, emerges as the primary source of error. This limitation constrains the broader adoption and application of GNSS positioning technology in the deformation monitoring of structures and geographical environments [109]. The exploration of the multipath error mitigation algorithm has great application value and research significance for high-accuracy deformation monitoring.

4.2. Precise Positioning of Urban Areas

With the increase in urbanization, the demand for location information services, such as mobile phones and vehicles, in urban areas is increasing. According to the 2015 “GNSS Market Report” of the European Union, the two major application markets, location service (LBS) and road navigation, have already occupied a dominant position (91%) in GNSS revenue. GNSS technology in the urban area environment has also received extensive research attention and been widely applied. There is a complex geographical and architectural environment in urban areas, which is mainly due to its large number of buildings and the green environment being scattered in the city. In the application of GNSS positioning techniques within urban environments, the dense positioning of buildings introduces a significant challenge, namely, the occurrence of pronounced reflections of satellite signals during signal propagation. This phenomenon results in a formidable multipath effect, substantially impairing the accuracy and reliability of positioning in urban settings [110]. Xu et al. [111] proposed a multipath estimation, detection, and mitigation method for carrier-phase observations. The experimental results in urban environments showed that the robustness and accuracy of navigation positioning were improved. Lu et al. [112] analyzed and verified the weakening effect of MHM and T-MHM on the PPP multipath effect of the BDS-3 system in a complex urban environment.

The multipath errors in the urban area are mainly divided into non-line-of-sight signal (NLOS) and reflected multipath effects. These two types of errors are essentially caused by the coherent signal of the extra path, and the difference lies in the participation of the direct signal or not. They often co-exist in urban environments, such as dense buildings and elevated areas, causing complex and obvious positioning errors. Due to the difficulty of eliminating these errors through baseline difference technology and the difficulty of obtaining a unified parameterized expression, it has a serious impact on the precise positioning of the urban environment [113]. Therefore, it is of great application value and significance to study the error correction methods of NLOS signals and reflection multipath effects for the achievement of GNSS high-precision positioning in the disciplines of crowd vehicle route navigation and driverless vehicles driving in urban areas [114].

5. Conclusions

The mitigation of GNSS carrier-phase multipath errors is a hot topic with great research significance in the field of navigation signal error processing. Scholars globally have conducted considerable research on the mitigation of multipath errors from various perspectives. In over 30 years of development, there has been notable progress in the research on methods to mitigate GNSS carrier-phase multipath errors. This paper reviewed and summarized the research on GNSS carrier-phase multipath error mitigation in recent years, with a primary focus on introducing the mitigation method of carrier-phase multipath errors from the station side based on software data processing. At present, the sidereal filtering method based on the time domain repetition characteristics of multipath errors and the multipath hemispherical map method based on the spatial domain repetition characteristics of multipath errors are the future research hotspots of multipath error data processing methods.

Future research directions of multipath error mitigation methods could focus on the following three aspects:

• Extend the current multipath error correction modeling method to the multi-frequency data of multi-GNSS systems, including GPS, BDS, Galileo, GLONASS, and other systems. Zou et al. [115] extended the MHM method and proposed a MHGM (multi-point hemispherical grid model, MHGM) method suitable for multi-GNSS systems. This approach enabled the fusion of observation data from different GNSS systems for MHGM modeling, demonstrating a significant attenuation effect on the multipath errors of GNSS signals. At present, the fusion processing of multi-system and multi-frequency GNSS data has emerged as the future trend in satellite positioning [116]. Research into multipath error processing methods suitable for multi-system and multi-frequency GNSS data constitutes a focal point for future investigations.
• Enhance the effectiveness of multipath mitigation methods in practical applications. In order to improve the positioning accuracy and operating efficiency in actual engineering practice, research on multipath error mitigation should be developed to achieve real-time application, intelligence [117], and engineering application, and the actual application scenarios should be extended to single-point positioning, dynamic scenes, and more complex environments with severe occlusions.
• Integrate deep learning and machine learning technology into multipath error mitigation. Xu and Tao [118] used a combination of deep learning network long short-term memory network (LSTM) and EMD to predict and weaken the impact of multipath effects. Tao et al. [119] constructed a time–frequency mask and convolutional neural network (TFM–CNN) model, which had a remarkable effect on separating the multiple paths of GNSS observation sequences in real-time deformation monitoring. Gong et al. [120] used the K-means clustering algorithm from machine learning to distinguish direct signals and reflected signals in urban environments to achieve the purpose of improving positioning accuracy. By processing GNSS data through deep learning and machine learning technology, the strengths of these approaches are leveraged to improve the capability of handling GNSS data and enhance the accuracy and reliability of GNSS positioning results.