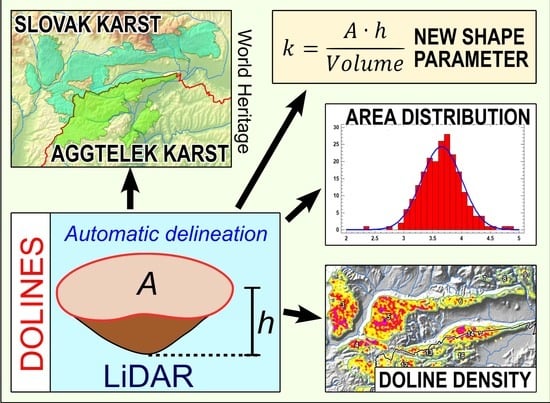
LiDAR-Based Morphometry of Dolines in Aggtelek Karst (Hungary) and Slovak Karst (Slovakia)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Base Data
2.3. Methodology
- Smoothing of the DTM to remove spurious errors.
- Filling of pits smaller than true dolines (by setting the appropriate Z-limit). (In the case of a too-small Z-limit, there are many false positives, i.e., features outlined by the algorithm that are not true dolines. In the case of a too-large Z-limit, there are many false negatives, i.e., dolines that are not recognized by the algorithm. In [18], it was demonstrated that 1 m is the optimal value for Aggtelek Karst; thus, in the present analysis, the same value was used as the Z-limit.) The result is the “filled DTM”.
- Determination of flow directions based on the filled DTM.
- Identification of the remaining sinks (which are deeper than the above Z-limit): these are the “sink points”.
- Delineation of watersheds belonging to the sink points.
- Filling of depressions up to the level of the lowermost point of their rim. The result is the “zonal-filled DTM”.
- Calculation of the difference between the “zonal-filled DTM” and the “filled DTM”: this is the depth.
- Delineation of areas where the depth is larger than 0: these are the dolines (as raster data).
- Conversion of dolines into a polygon shape file for further analysis.
- Calculation of the morphometric characteristics of sinkholes.
3. Results
3.1. Features Identified in LiDAR versus TOPO Data
3.2. Doline Spatial Distribution Parameters
3.3. Doline Area Empirical Distributions
3.4. Parameters Characterizing the Vertical Shape
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cvijić, J. Das Karstphänomen. Versuch Einer Morphologischen Monographie; Hölzel: Wien, Austria, 1893; Volume 5, pp. 218–329. [Google Scholar]
- Ford, D.; Williams, P.D. Karst Hydrogeology and Geomorphology; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Williams, P.W. Illustrating Morphometric Analysis of Karst with Examples from New Guinea. Z. Für Geomorphol. 1971, 15, 40–61. [Google Scholar] [CrossRef]
- Williams, P.W. Morphometric Analysis of Polygonal Karst in New Guinea. GSA Bull. 1972, 83, 761–796. [Google Scholar] [CrossRef]
- Orndorff, R.C.; Weary, D.J.; Lagueux, K.M. Geographic Information Systems Analysis of Geologic Controls on the Distribution on Dolines in the Ozarks of South-Central Missouri, USA. Acta Carsol. 2000, 29, 161–175. [Google Scholar] [CrossRef]
- Gao, Y.; Alexander, E.C., Jr.; Tipping, R.G. The Development of a Karst Feature Database for Southeastern Minnesota. J. Cave Karst Stud. 2002, 64, 51–57. [Google Scholar]
- Denizman, C. Morphometric and Spatial Distribution Parameters of Karstic Depressions, Lower Suwanee River Basin, Florida. J. Cave Karst Stud. 2003, 65, 29–35. [Google Scholar]
- Florea, L.J. Using State-Wide GIS Data to Identify the Coincidence Betwen Sinkholes and Geologic Structure. J. Cave Karst Stud. 2005, 67, 120–124. [Google Scholar]
- Faivre, S.; Pahernik, M. Structural Influences on the Spatial Distribution of Dolines, Island of Brac, Croatia. Z. Für Geomorphol. 2007, 51, 487–503. [Google Scholar] [CrossRef]
- Telbisz, T.; Dragušica, H.; Nagy, B. Doline Morphometric Analysis and Karst Morphology of Biokovo Mt (Croatia) Based on Field Observations and Digital Terrain Analysis. Hrvat. Geogr. Glas. 2009, 71, 5–22. [Google Scholar] [CrossRef]
- Gallay, M.; Kaňuk, J.; Petrvalská, A. Využitie Údajov Leteckého Laserového Skenovania vo Výskume Krasovej Krajiny Na Slovensku—Na Príklade Východnej Časti Slovenského Krasu. (Using the Airborne Laser Scanning Data in Studying the Karst Landscape of Slovakia—Case Study of the Eastern Part of the Slovak Karst). Slov. Kras 2013, 51, 99–108. [Google Scholar]
- Obu, J.; Podobnikar, T. Algoritem Za Prepoznavanje Kraških Kotanj Na Podlagi Digitalnega Modela Reliefa (Algorithm for Karst Depression Recognition Using Digital Terrain Model). Geod. Vestn. 2013, 57, 260–270. [Google Scholar] [CrossRef]
- Rahimi, M.; Alexander, C. Locating Sinkholes in LiDAR Coverage of a Glacio-Fluvial Karst, Winona County, MN. In Proceedings of the Full Proceedings of the Thirteenth Multidisciplinary Conference on Sinkholes and the Engineering and Environmental Impacts of Karst, Carlsbad, NM, USA, 6–10 May 2013; National Cave and Karst Research Institute: Carlsbad, NM, USA, 2013; pp. 469–480. [Google Scholar]
- Zhu, J.; Taylor, T.P.; Currens, J.C.; Crawford, M.M. Improved Karst Sinkhole Mapping in Kentucky Using LiDAR Techniques: A Pilot Study in Floyds Fork Watershed. J. Cave Karst Stud. 2014, 76, 207–216. [Google Scholar] [CrossRef]
- Kobal, M.; Bertoncelj, I.; Pirotti, F.; Dakskobler, I.; Kutnar, L. Using Lidar Data to Analyse Sinkhole Characteristics Relevant for Understory Vegetation under Forest Cover—Case Study of a High Karst Area in the Dinaric Mountains. PLoS ONE 2015, 10, e0122070. [Google Scholar] [CrossRef]
- Bauer, C. Analysis of Dolines Using Multiple Methods Applied to Airborne Laser Scanning Data. Geomorphology 2015, 250, 78–88. [Google Scholar] [CrossRef]
- Jeanpert, J.; Genthon, P.; Maurizot, P.; Folio, J.-L.; Vendé-Leclerc, M.; Sérino, J.; Join, J.-L.; Iseppi, M. Morphology and Distribution of Dolines on Ultramafic Rocks from Airborne LiDAR Data: The Case of Southern Grande Terre in New Caledonia (SW Pacific). Earth Surf. Process. Landf. 2016, 41, 1854–1868. [Google Scholar] [CrossRef]
- Telbisz, T.; Látos, T.; Deák, M.; Székely, B.; Koma, Z.; Standovár, T. The Advantage of Lidar Digital Terrain Models in Doline Morphometry Compared to Topographic Map Based Datasets—Aggtelek Karst (Hungary) as an Example. Acta Carsol. 2016, 45, 5–18. [Google Scholar] [CrossRef]
- Wu, Q.; Deng, C.; Chen, Z. Automated Delineation of Karst Sinkholes from LiDAR-Derived Digital Elevation Models. Geomorphology 2016, 266, 1–10. [Google Scholar] [CrossRef]
- Hofierka, J.; Gallay, M.; Bandura, P.; Šašak, J. Identification of Karst Sinkholes in a Forested Karst Landscape Using Airborne Laser Scanning Data and Water Flow Analysis. Geomorphology 2018, 308, 265–277. [Google Scholar] [CrossRef]
- Verbovšek, T.; Gabor, L. Morphometric Properties of Dolines in Matarsko Podolje, SW Slovenia. Environ. Earth Sci. 2019, 78, 396. [Google Scholar] [CrossRef]
- Bauer, C.; Wagner, T. From Landform Inventories to Landscape Evolution?—Karst Development in the Central Styrian Karst (Austria). Geomorphology 2024, 447, 109024. [Google Scholar] [CrossRef]
- Látos, T.; Telbisz, T. LiDAR És UAV Alapú Digitális Domborzatmodellek Összevetése Töbör-Morfometria Szempontjából a Jósvafői-Fennsík Példáján. Karsztfejlődés 2018, 23, 19–30. [Google Scholar] [CrossRef]
- Oliveira, S.; Moura, D.; Boski, T.; Horta, J. Coastal Paleokarst Landforms: A Morphometric Approach via UAV for Coastal Management (Algarve, Portugal Case Study). Ocean Coast. Manag. 2019, 167, 245–261. [Google Scholar] [CrossRef]
- Menezes, D.F.; Bezerra, F.H.; Balsamo, F.; Arcari, A.; Maia, R.P.; Cazarin, C.L. Subsidence Rings and Fracture Pattern around Dolines in Carbonate Platforms—Implications for Evolution and Petrophysical Properties of Collapse Structures. Mar. Pet. Geol. 2020, 113, 104113. [Google Scholar] [CrossRef]
- Utlu, M.; Öztürk, M.Z. Comparison of Morphometric Characteristics of Dolines Delineated from TOPO-Maps and UAV-DEMs. Environ. Earth Sci. 2023, 82, 165. [Google Scholar] [CrossRef]
- Ford, D. Jovan Cvijić and the Founding of Karst Geomorphology. Environ. Geol. 2007, 51, 675–684. [Google Scholar] [CrossRef]
- Kemmerly, P.R. Spatial Analysis of a Karst Depression Population: Clues to Genesis. GSA Bull. 1982, 93, 1078–1086. [Google Scholar] [CrossRef]
- Troester, J.W.; White, E.L.; White, W.B. A Comparison of Sinkhole Depth Frequency Distributions in Temperate and Tropic Karst Regions. In Proceedings of the Multidisciplinary Conference on Sinkholes. 1, Orlando, FL, USA, 15–17 October 1984; pp. 65–73. [Google Scholar]
- Kemmerly, P.R. Exploring a Contagion Model for Karst-Terrane Evolution. GSA Bull. 1986, 97, 619–625. [Google Scholar] [CrossRef]
- Telbisz, T. Új Megközelítések a Töbör-Morfológiában Az Aggteleki-Karszt Példáján (New Perspectives in Doline-Morphometry—Aggtelek Karst as an Example). Földrajzi Közlemények 2001, 125, 95–108. [Google Scholar]
- Pahernik, M. Spatial Density of Dolines in the Croatian Territory. Hrvat. Geogr. Glas. 2012, 74, 5–26. [Google Scholar] [CrossRef]
- Veress, M.; Telbisz, T.; Tóth, G.; Lóczy, D.; Ruban, D.A.; Gutak, J. Glaciokarsts; Springer Geography; Springer International Publishing: Cham, Swizterland, 2019; ISBN 978-3-319-97291-6. [Google Scholar]
- Gao, Y.; Alexander, E.C.; Barnes, R.J. Karst Database Implementation in Minnesota: Analysis of Sinkhole Distribution. Environ. Geol. 2005, 47, 1083–1098. [Google Scholar] [CrossRef]
- Plan, L.; Decker, K. Quantitative Karst Morphology of the Hochschwab Plateau, Eastern Alps, Austria. Z. Geomorphol. Suppl. Issues 2006, 147, 29–54. [Google Scholar]
- Brinkmann, R.; Parise, M.; Dye, D. Sinkhole Distribution in a Rapidly Developing Urban Environment: Hillsborough County, Tampa Bay Area, Florida. Eng. Geol. 2008, 99, 169–184. [Google Scholar] [CrossRef]
- Pardo-Iguzquiza, E.; Pulido-Bosch, A.; Lopez-Chicano, M.; Duran, J. Morphometric Analysis of Karst Depressions on a Mediterranean Karst Massif. Geogr. Ann. Ser. A Phys. Geogr. 2016, 98, 247–263. [Google Scholar] [CrossRef]
- Pardo-Igúzquiza, E.; Dowd, P.A.; Durán, J.J.; Robledo-Ardila, P. A Review of Fractals in Karst. Int. J. Speleol. 2018, 48, 11–20. [Google Scholar] [CrossRef]
- Pardo-Igúzquiza, E.; Dowd, P.A.; Telbisz, T. On the Size-Distribution of Solution Dolines in Carbonate Karst: Lognormal or Power Model? Geomorphology 2020, 351, 106972. [Google Scholar] [CrossRef]
- Šušteršič, F. Are “Collapse Dolines” Formed Only by Collapse? Acta Carsol. 2000, 29, 213–230. [Google Scholar] [CrossRef]
- Šušteršič, F. A Power Function Model for the Basic Geometry of Solution Dolines: Considerations from the Classical Karst of South-Central Slovenia. Earth Surf. Process. Landf. 2006, 31, 293–302. [Google Scholar] [CrossRef]
- Yakar, M.; Yilmaz, H.M.; Mutluoglu, O. Performance of Photogrammetric and Terrestrial Laser Scanning Methods in Volume Computing of Excavtion and Filling Areas. Arab. J. Sci. Eng. 2014, 39, 387–394. [Google Scholar] [CrossRef]
- Lu, B.; Zhu, J.; Ge, Y.; Chen, Q.; Wen, Z.; Liu, G.; Li, L. Automated Determination of the Volume of Loose Engineering Deposits Using Terrestrial Laser Scanning. Remote Sens. 2023, 15, 4604. [Google Scholar] [CrossRef]
- Slattery, K.T.; Slattery, D.K.; Peterson, J.P. Road Construction Earthwork Volume Calculation Using Three-Dimensional Laser Scanning. J. Surv. Eng. 2012, 138, 96–99. [Google Scholar] [CrossRef]
- Bisson, M.; Spinetti, C.; Andronico, D.; Palaseanu-Lovejoy, M.; Fabrizia Buongiorno, M.; Alexandrov, O.; Cecere, T. Ten Years of Volcanic Activity at Mt Etna: High-Resolution Mapping and Accurate Quantification of the Morphological Changes by Pleiades and Lidar Data. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102369. [Google Scholar] [CrossRef]
- Kósik, S.; Németh, K.; Rees, C. Integrating LiDAR to Unravel the Volcanic Architecture and Eruptive History of the Peralkaline Tūhua (Mayor Island) Volcano, New Zealand. Geomorphology 2022, 418, 108481. [Google Scholar] [CrossRef]
- Schmid, B.M.; Williams, D.L.; Chong, C.-S.; Kenney, M.D.; Dickey, J.B.; Ashley, P. Use of Digital Photogrammetry and LiDAR Techniques to Quantify Time-Series Dune Volume Estimates of the Keeler Dunes Complex, Owens Valley, California. Aeolian Res. 2022, 54, 100764. [Google Scholar] [CrossRef]
- Zheng, Z.; Du, S.; Taubenböck, H.; Zhang, X. Remote Sensing Techniques in the Investigation of Aeolian Sand Dunes: A Review of Recent Advances. Remote Sens. Environ. 2022, 271, 112913. [Google Scholar] [CrossRef]
- Bernard, T.G.; Lague, D.; Steer, P. Beyond 2D Landslide Inventories and Their Rollover: Synoptic 3D Inventories and Volume from Repeat Lidar Data. Earth Surf. Dyn. 2021, 9, 1013–1044. [Google Scholar] [CrossRef]
- Faivre, S.; Reiffsteck, P. From Doline Distribution to Tectonics Movements Example of the Velebit Mountain Range, Croatia. Acta Carsol. 2002, 31, 139–154. [Google Scholar] [CrossRef]
- Telbisz, T.; Mari, L.; Szabó, L. Geomorphological Characteristics of the Italian Side of Canin Massif (Julian Alps) Using Digital Terrain Analysis and Field Observations. Acta Carsol. 2011, 40, 255–266. [Google Scholar] [CrossRef]
- Cucchi, F.; Zini, L.; Calligaris, C. Le Acque Del Carso Classico. Vodonosnik Klasičnega Krasa. Projekt Hydrokarst; Edizioni Università di Trieste: Trieste, Italy, 2015; ISBN 978-88-8303-621-7. [Google Scholar]
- Öztürk, M.Z.; Şimşek, M.; Şener, M.F.; Utlu, M. GIS Based Analysis of Doline Density on Taurus Mountains, Turkey. Environ. Earth Sci. 2018, 77, 536. [Google Scholar] [CrossRef]
- Öztürk, M. Fluvio-Karstic Evolution of the Taşeli Plateau (Central Taurus, Turkey). Turk. J. Earth Sci. 2020, 29, 733–746. [Google Scholar] [CrossRef]
- Lončar, N.; Grcić, I. Gis-Based Analysis of Doline Density on Miljevci Karst Plateau (Croatia). Acta Carsol. 2022, 51, 5–17. [Google Scholar] [CrossRef]
- Bella, P.; Gruber, P.; Gaál, L.; Papáč, V.; Bárány Kevei, I. Caves of Aggtelek and Slovak Karsts, Northern Hungary and Southern Slovakia. Z. Für Geomorphol. Suppl. Issues 2021, 62, 19–47. [Google Scholar] [CrossRef]
- Telbisz, T.; Mari, L.; Gessert, A.; Dická, J.N.; Gruber, P. Attitudes and Perceptions of Local Residents and Tourists—A Comparative Study of the Twin National Parks of Aggtelek (Hungary) and Slovak Karst (Slovakia). Acta Carsol. 2022, 51, 93–109. [Google Scholar] [CrossRef]
- Ferreira, C.F.; Hussain, Y.; Uagoda, R. A Semi-Automatic Approach for Doline Mapping in Brazilian Covered Karst: The Way Forward to Vulnerability Assessment. Acta Carsol. 2022, 51, 19–31. [Google Scholar] [CrossRef]
- Leone, G.; Catani, V.; Pagnozzi, M.; Ginolfi, M.; Testa, G.; Esposito, L.; Fiorillo, F. Hydrological Features of Matese Karst Massif, Focused on Endorheic Areas, Dolines and Hydroelectric Exploitation. J. Maps 2023, 19, 2144497. [Google Scholar] [CrossRef]
- Less, G.; Grill, J.; Róth, L.; Szentpétery, I.; Gyuricza, G. Geological Map of the Aggtelek-Rudabánya-Mts., 1:25.000; Hungarian Geological Institute: Budapest, Hungary, 1988. [Google Scholar]
- Mello, J.; Elečko, M.; Pristaš, J.; Reichwalder, P.; Snopko, L.; Vass, D.; Vozárová, A. Geologická Mapa Slovenského Krasu. Geological Map of the Slovenský Kras Mts; GSSR: Bratislava, Slovakia, 1996. [Google Scholar]
- Mello, J. Vysvetlivky Ku Geologickej Mape Slovenského Krasu 1:50000; Štátny Geologický ústav Dionýza Štúra: Bratislava, Slovakia, 1997. [Google Scholar]
- Less, G. Polyphase Evolution of the Structure of the Aggtelek-Rudabánya Mountains (NE Hungary), the Southernmost Element of the Inner Western Carpathians—A Review. Slovak Geol. Mag. 2000, 6, 260–268. [Google Scholar]
- Az Aggtelek–Rudabányai-Hegység Földtana. Magyarázó Az Aggtelek–Rudabányai-Hegység 1988-Ban Megjelent 1:25000 Méretarányú Fedetlen Földtani Térképéhez; Less, G., Szentpétery, I., Eds.; Magyar Állami Földtani Intézet: Budapest, Hungary, 2006. [Google Scholar]
- Gaál, L.; Bella, P. Vplyv Tektonických Pohybov Na Geomorfologický Vývoj Západnej Časti Slovenského Krasu (The Influence of Tectonic Movements to the Geomorphological Development of the Western Part of Slovak Karst). Slov. Kras (Acta Carsol. Slovaca) 2005, 43, 17–36. [Google Scholar]
- Gaál, Ľ.; Bella, P.; Jakál, J. Slovak Karst: Surface and Subsurface Geodiversity of the Karst Plateau in the Temperate Climate Zone. In Landscapes and Landforms of Slovakia; Lehotský, M., Boltižiar, M., Eds.; World Geomorphological Landscapes; Springer International Publishing: Cham, Swizterland, 2022; pp. 323–349. ISBN 978-3-030-89293-7. [Google Scholar]
- Mazur, E. Slovenský Kras. Regionalna Fyzikogeografická Analyza. In Proceedings of the 6th International Congress of Speleology; Pano, V., Ed.; Academia: Praha, Czech Republic, 1973; p. 117. [Google Scholar]
- Jakál, J. Kras Silickej Planiny; Osveta: Martin, Slovakia, 1975. [Google Scholar]
- Bosák, P.; Horáček, I.; Panoš, V. Paleokarst of Czechoslovakia. In Paleokarst. A Systematic and Regional Review; Bosák, P., Ford, D.C., Głazek, J., Horáček, I., Eds.; Paleokarst; Elsevier: Amsterdam, The Netherlands, 1990; Volume 1, pp. 107–135. ISBN 978-1-4832-9176-5. [Google Scholar]
- Móga, J. Felszínalaktani Megfigyelések a Gömör-Tornai-Karszton. Ph.D. Thesis, Department of Physical Geography, Eötvös Loránd University, Budapest, Hungary, 1998. [Google Scholar]
- Gessert, A. Geomorphology of the Slovak Karst (Eastern Part). J. Maps 2016, 12, 285–288. [Google Scholar] [CrossRef]
- Zámbó, L. Az Aggteleki-Karszt Felszínalaktani Jellemzése. Földrajzi Értesítő 1998, 47, 359–378. [Google Scholar]
- Láng, S. Geomorfológiai Tanulmányok Az Aggteleki Karsztvidéken. Földrajzi Értesítő 1955, 6, 1–17. [Google Scholar]
- Mezősi, G. A Sajó-Bódva Köze Felszínfejlődése. Földrajzi Értesítő 1984, 33, 181–205. [Google Scholar]
- Petrvalská, A. Vývoj Názorov Na Vznik a Genézu Zarovnaných Povrchov Slovenskeho Krasu (Development of Conceptions Concerning Origins and Genesis of Planation Surface of Slovak Karst). Acta Geogr. Univ. Comen. 2010, 54, 81–99. [Google Scholar]
- Veselskỳ, M.; Bandura, P.; Burian, L.; Harciníková, T.; Bella, P. Semi-Automated Recognition of Planation Surfaces and Other Flat Landforms: A Case Study from the Aggtelek Karst, Hungary. Open Geosci. 2015, 7, 799–811. [Google Scholar] [CrossRef]
- Bella, P.; Bosák, P.; Braucher, R.; Pruner, P.; Hercman, H.; Minár, J.; Veselský, M.; Holec, J.; Léanni, L. Multi-Level Domica–Baradla Cave System (Slovakia, Hungary): Middle Pliocene–Pleistocene Evolution and Implications for the Denudation Chronology of the Western Carpathians. Geomorphology 2019, 327, 62–79. [Google Scholar] [CrossRef]
- Kercsmár, Z.; Selmeczi, I.; Budai, T.; Less, G.; Konrád, G. Geology of the Karst Terrains in Hungary. In Cave and Karst Systems of Hungary; Veress, M., Leél-Őssy, S., Eds.; Cave and Karst Systems of the World; Springer International Publishing: Cham, Swizterland, 2022; pp. 63–116. ISBN 978-3-030-92959-6. [Google Scholar]
- Móga, J.; Veress, M. The Geomorphic Evolution of Karsts and Karstic Surfaces. In Cave and Karst Systems of Hungary; Veress, M., Leél-Őssy, S., Eds.; Cave and Karst Systems of the World; Springer International Publishing: Cham, Swizterland, 2022; pp. 161–177. ISBN 978-3-030-92959-6. [Google Scholar]
- Petrvalská, A. Morfometrická Analýza Závrtov Na Príklade Jasovskej Planiny, Slovenský Kras. (Morphometric Analysis of Dolines on Jasovská Plateau, Slovak Karst). Geomorphol. Slovaca Bohem. 2010, 10, 33–44. [Google Scholar]
- Veress, M. The Surface Morphology of Karsts in Hungary. In Cave and Karst Systems of Hungary; Veress, M., Leél-Őssy, S., Eds.; Cave and Karst Systems of the World; Springer International Publishing: Cham, Swizterland, 2022; pp. 179–247. ISBN 978-3-030-92959-6. [Google Scholar]
- Móga, J. Reconstruction of the Development History of Karstic Water Networks on the Southern Part of the Gömör-Torna Karst on the Bases of Ruined Caves and Landforms. Acta Carsol. 1999, 28, 159–174. [Google Scholar] [CrossRef]
- UNESCO World Heritage. Caves of Aggtelek Karst and Slovak Karst. Available online: https://whc.unesco.org/en/list/725/ (accessed on 17 December 2023).
- Jakucs, L. Adatok Az Aggteleki Hegység És Barlangjainak Morfogenetikájához (Data to the Morphogenetics of Caves of Aggtelek Karst). Földrajzi Közlemények 1956, 80, 25–38. [Google Scholar]
- Sásdi, L. Az Aggtelek–Rudabányai-Hegység Karsztjának Földtani Fejlődéstörténete. Karszt És Barlang 1990, 1, 3–8. [Google Scholar]
- Hevesi, A. Magyarország Karsztvidékeinek Kialakulása És Formakincse I. (Evolution and Landforms of Karst Terrains in Hungary I). Földrajzi Közlemények 1991, 115, 25–35. [Google Scholar]
- Gaál, L. Prehlad Geomorfologického Vývoja Územia. In Vysvetlivky Ku Geologickej Mape Slovenského Krasu 1:50.000 (Overview of the Geomorphological Evolution, Explanations to the Geological Map of the Slovak Karst); Vyd Dionýza Štúra: Bratislava, Slovakia, 1997. [Google Scholar]
- Bárány-Kevei, I.; Mezősi, G. New Morphometrical Parameters for Explanation of Karst Development. Acta Geogr. Szeged. 1994, 31, 27–33. [Google Scholar]
- Veress, M. Adalékok Az Aggteleki-Fennsík Völgyeinek Fejlődéséhez. Karszt És Barlang 2008, 1, 3–12. [Google Scholar]
- Gessert, A.; Telbisz, T. Geomorfologické špecifiká reliéfu Zádielskej planiny v Slovenskom Krase. Geomorphological particularities of the Zádiel Plateau relief in the Slovak Karst. Slov. Kras Acta Carsologica Slovaca 2017, 55, 47–60. [Google Scholar]
- Geodetický a Kartografický ústav Bratislava Geoportál. Available online: https://www.geoportal.sk/en/zbgis/als_dmr/ (accessed on 9 February 2023).
- Geoportál Základná Mapa SR. Available online: http://www.geoportal.sk/sk/archiv/statne-mapy/zakladna-mapa-sr/ (accessed on 19 January 2024).
- Lechner, T. Topográfiai Térkép. Available online: https://lechnerkozpont.hu/node/478 (accessed on 19 January 2024).
- Pardo-Igúzquiza, E.; Durán, J.J.; Dowd, P.A. Automatic Detection and Delineation of Karst Terrain Depressions and Its Application in Geomorphological Mapping and Morphometric Analysis. Acta Carsol. 2013, 42, 17–24. [Google Scholar] [CrossRef]
- Kranjc, A. Some Large Dolines in the Dinaric Karst. Cave Karst Sci. 2005, 32, 99–100. [Google Scholar]
- Ćalić, J. Karstic Uvala Revisited: Toward a Redefinition of the Term. Geomorphology 2011, 134, 32–42. [Google Scholar] [CrossRef]
- Telbisz, T. Lidar-Based Morphometry of Conical Hills in Temperate Karst Areas in Slovenia. Remote Sens. 2021, 13, 2668. [Google Scholar] [CrossRef]
- Šegina, E.; Benac, Č.; Rubinić, J.; Knez, M. Morphometric Analyses of Dolines—The Problem of Delineation and Calculation of Basic Parameters. Acta Carsol. 2018, 47, 23–33. [Google Scholar] [CrossRef]
- Čeru, T.; Šegina, E.; Gosar, A. Geomorphological Dating of Pleistocene Conglomerates in Central Slovenia Based on Spatial Analyses of Dolines Using LiDAR and Ground Penetrating Radar. Remote Sens. 2017, 9, 1213. [Google Scholar] [CrossRef]
- Davis, J.C. Statistics and Data Analysis in Geology, 3rd ed.; JohnWiley & Sons: New York, NY, USA, 2002; ISBN 978-0-471-17275-8. [Google Scholar]
- Telbisz, T.; Mari, L.; Ćalić, J. Doline Morphometry of Mt. Miroč Using GIS Methods. Glas. Srp. Geogr. Drus. 2007, 87, 21–30. [Google Scholar] [CrossRef]
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The Shuttle Radar Topography Mission—A New Class of Digital Elevation Models Acquired by Spaceborne Radar. ISPRS J. Photogramm. Remote Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
- Limpert, E.; Stahel, W.A.; Abbt, M. Log-Normal Distributions across the Sciences: Keys and Clues: On the Charms of Statistics, and How Mechanical Models Resembling Gambling Machines Offer a Link to a Handy Way to Characterize Log-Normal Distributions, Which Can Provide Deeper Insight into Variability and Probability—Normal or Log-Normal: That Is the Question. BioScience 2001, 51, 341–352. [Google Scholar] [CrossRef]
- Gibrat, R. Les Inégalites Économiques; Sirey: Paris, France, 1931. [Google Scholar]
- Santarelli, E.; Klomp, L.; Thurik, A.R. Gibrat’s Law: An Overview of the Empirical Literature. In Entrepreneurship, Growth, and Innovation: The Dynamics of Firms and Industries; Santarelli, E., Ed.; International Studies in Entrepreneurship; Springer: Boston, MA, USA, 2006; pp. 41–73. ISBN 978-0-387-32314-5. [Google Scholar]
- Mitzenmacher, M. A Brief History of Generative Models for Power Law and Lognormal Distributions. Internet Math. 2004, 1, 226–251. [Google Scholar] [CrossRef]
- Barabási, A.L. Network Science 4. The Scale-Free Property; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Gabrovšek, F. On Denudation Rates in Karst. Acta Carsol. 2007, 36, 7–13. [Google Scholar] [CrossRef]
- Matsushi, Y.; Hattanji, T.; Akiyama, S.; Sasa, K.; Takahashi, T.; Sueki, K.; Matsukura, Y. Evolution of Solution Dolines Inferred from Cosmogenic 36Cl in Calcite. Geology 2010, 38, 1039–1042. [Google Scholar] [CrossRef]
- Xu, S.; Liu, C.; Freeman, S.; Lang, Y.; Schnabel, C.; Tu, C.; Wilcken, K.; Zhao, Z. In-Situ Cosmogenic 36Cl Denudation Rates of Carbonates in Guizhou Karst Area. Chin. Sci. Bull. 2013, 58, 2473–2479. [Google Scholar] [CrossRef]
- Sartégou, A.; Bourlès, D.L.; Blard, P.-H.; Braucher, R.; Tibari, B.; Zimmermann, L.; Leanni, L.; Aumaître, G.; Keddadouche, K. Deciphering Landscape Evolution with Karstic Networks: A Pyrenean Case Study. Quat. Geochronol. 2018, 43, 12–29. [Google Scholar] [CrossRef]
- Krklec, K.; Domínguez-Villar, D.; Braucher, R.; Perica, D.; Mrak, I. Morphometric Comparison of Weathering Features on Side by Side Carbonate Rock Surfaces with Different Exposure Ages―A Case from the Croatian Coast. Quat. Int. 2018, 494, 275–285. [Google Scholar] [CrossRef]
- Shen, H.; Sasa, K.; Meng, Q.; Matsumura, M.; Matsunaka, T.; Hosoya, S.; Takahashi, T.; Honda, M.; Sueki, K.; He, M.; et al. Exposure Age Dating of Chinese Tiankengs by 36Cl-AMS. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2019, 459, 29–35. [Google Scholar] [CrossRef]
- Krklec, K.; Braucher, R.; Perica, D.; Domínguez-Villar, D. Long-Term Denudation Rate of Karstic North Dalmatian Plain (Croatia) Calculated from 36Cl Cosmogenic Nuclides. Geomorphology 2022, 413, 108358. [Google Scholar] [CrossRef]
- Plan, L. Factors Controlling Carbonate Dissolution Rates Quantified in a Field Test in the Austrian Alps. Geomorphology 2005, 68, 201–212. [Google Scholar] [CrossRef]
- Gabrovšek, F. On Concepts and Methods for the Estimation of Dissolutional Denudation Rates in Karst Areas. Geomorphology 2009, 106, 9–14. [Google Scholar] [CrossRef]
- Gessert, A.; Sládek, I.; Straková, V.; Braun, M.; Heim, E.; Czébely, A.; Palcsu, L. Ionic Runoff as a Way to Determine the Degree of Karst Denudation (Case Study Jasov Plateau, Slovak Karst, Slovakia). Water 2021, 13, 1449. [Google Scholar] [CrossRef]
















| Id | Plateau Name | Number of Dolines | Doline Density (km−2) | Doline Area Ratio (%) | Doline–Area Mean (m2) | Doline–Area Median (m2) |
|---|---|---|---|---|---|---|
| 1 | Jelšavská | 38 | 12.6 | 8.5% | 6723 | 3863 |
| 2 | Koniarska | 213 | 17.3 | 11.0% | 6342 | 4657 |
| 3 | Plešivská | 946 | 28.4 | 14.4% | 5079 | 3597 |
| 4 | Bučina | 191 | 35.6 | 15.9% | 4474 | 3608 |
| 5 | Silická | 1436 | 29.9 | 16.3% | 5460 | 3930 |
| 6 | Horný | 170 | 12.8 | 6.0% | 4676 | 3540 |
| 7 | Žl’ab | 0 | 0.0 | 0.0% | n.d. | n.d. |
| 8 | Bôrčianska | 8 | 2.4 | 0.6% | 2408 | 636 |
| 9 | Zádielska | 30 | 3.8 | 2.9% | 7733 | 4888 |
| 10 | Jasovská | 152 | 3.2 | 1.6% | 4931 | 2732 |
| 11 | Kečovská-Haragistya | 380 | 15.8 | 9.6% | 6065 | 3419 |
| 12 | Nagyoldal | 148 | 23.3 | 10.8% | 4615 | 3544 |
| 13 | W-Alsó-hegy | 154 | 15.5 | 6.8% | 4378 | 2849 |
| 14 | E-Alsó-hegy | 645 | 30.0 | 13.6% | 4550 | 3177 |
| 15 | Szinpetri | 144 | 10.9 | 7.5% | 6929 | 5274 |
| 16 | Páska-bükk | 21 | 10.8 | 16.5% | 15,229 | 8469 |
| 17 | Aggtelek | 182 | 8.8 | 9.9% | 11,237 | 5934 |
| 18 | Rudabánya | 2 | 1.0 | 0.1% | 1254 | 1254 |
| 19 | Szalonna | 29 | 5.3 | 4.3% | 8094 | 4932 |
| 20 | Jósvafő | 66 | 33.0 | 16.0% | 4829 | 3333 |
| General Slope Angle Values for Different Percentiles | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| General Slope Calculated From | 1% | 5% | 10% | 25% | 50% | 75% | 90% | 95% | 99% |
| Unsmoothed SRTM 1″ | 1.0 | 1.6 | 2.1 | 3.1 | 4.5 | 6.4 | 8.2 | 9.7 | 12.8 |
| 3-cell mean-filtered SRTM 1″ | 0.7 | 1.2 | 1.6 | 2.5 | 3.9 | 5.6 | 7.4 | 8.7 | 11.8 |
| 5-cell mean-filtered SRTM 1″ | 0.5 | 1.0 | 1.3 | 2.3 | 3.7 | 5.3 | 7.0 | 8.4 | 11.9 |
| Lithology | Count | Percent of All Dolines (PAD) | Percent of Plateau Dolines (PPD) | Percent of Plateau Area (PPA) | PPD/PPA |
|---|---|---|---|---|---|
| Wetterstein Limestone | 3834 | 72.9% | 74.1% | 60.5% | 1.22 |
| Steinalm Limestone | 532 | 10.1% | 10.6% | 10.7% | 0.99 |
| Wetterstein Dolomite | 154 | 2.9% | 2.9% | 4.4% | 0.67 |
| Gutenstein Limestone | 121 | 2.3% | 2.3% | 2.7% | 0.87 |
| Reifling Limestone | 119 | 2.3% | 1.8% | 1.8% | 0.99 |
| Gutenstein Dolomite | 116 | 2.2% | 2.3% | 2.5% | 0.90 |
| Deluvial sediments | 71 | 1.3% | 0.9% | 3.0% | 0.32 |
| Waxeneck Limestone | 62 | 1.2% | 1.0% | 1.8% | 0.55 |
| Szin Beds | 61 | 1.2% | 0.8% | 2.1% | 0.40 |
| Gutenstein undistinguished | 49 | 0.9% | 0.8% | 1.4% | 0.54 |
| Id | Plateau Name | Chi-Square Statistic | Chi-Square p-Value | Kolmogorov–Smirnov D | Kolmogorov–Smirnov p-Value |
|---|---|---|---|---|---|
| 1 | Jelšavská | 12.5263 | 0.4850 | 0.1003 | 0.8394 |
| 2 | Koniarska | 26.0563 | 0.6723 | 0.0424 | 0.8376 |
| 3 | Plešivská | 115.8750 | 4.60 × 10−6 | 0.0507 | 0.0153 |
| 4 | Bučina | 24.3770 | 0.6615 | 0.0417 | 0.8936 |
| 5 | Silická | 137.2580 | 6.40 × 10−7 | 0.0449 | 0.0061 |
| 6 | Horný | 29.7647 | 0.3248 | 0.0978 | 0.0773 |
| 7 | Žl’ab | n.d. | n.d. | n.d. | n.d. |
| 8 | Bôrčianska | n.d. | n.d. | n.d. | n.d. |
| 9 | Zádielska | 13.0000 | 0.3690 | 0.1119 | 0.8468 |
| 10 | Jasovská | 26.5789 | 0.4317 | 0.0616 | 0.6121 |
| 11 | Kečovská-Haragistya | 28.2737 | 0.8749 | 0.0361 | 0.7057 |
| 12 | Nagyoldal | 20.3784 | 0.7267 | 0.0727 | 0.4210 |
| 13 | W-Alsó-hegy | 26.7792 | 0.4210 | 0.0545 | 0.7497 |
| 14 | E-Alsó-hegy | 69.0791 | 0.0247 | 0.0419 | 0.2085 |
| 15 | Szinpetri | 31.0000 | 0.1890 | 0.0776 | 0.3543 |
| 16 | Páska-bükk | 3.1429 | 0.9779 | 0.1060 | 0.9723 |
| 17 | Aggtelek | 39.0879 | 0.0795 | 0.0541 | 0.6617 |
| 18 | Rudabánya | n.d. | n.d. | n.d. | n.d. |
| 19 | Szalonna | 5.5690 | 0.2337 | 0.0859 | 0.9830 |
| 20 | Jósvafő | 14.6061 | 0.6238 | 0.0748 | 0.8535 |
| Id | Plateau Name | Doline Depth, Mean (m) | Depth-to-Diameter Ratio | Volume, Mean (m3) | 3D-Shape Parameter (k), Mean | Mean Denudation Thickness (m) |
|---|---|---|---|---|---|---|
| 1 | Jelšavská | 7.6 | 0.0866 | 49,560 | 2.21 | 0.6265 |
| 2 | Koniarska | 8.3 | 0.0943 | 30,421 | 2.23 | 0.5265 |
| 3 | Plešivská | 8.8 | 0.1078 | 24,277 | 2.56 | 0.6897 |
| 4 | Bučina | 9.9 | 0.1285 | 23,161 | 2.34 | 0.8235 |
| 5 | Silická | 8.7 | 0.1063 | 25,009 | 2.41 | 0.7478 |
| 6 | Horný | 6.1 | 0.0777 | 14,870 | 2.40 | 0.1896 |
| 7 | Žl’ab | n.d. | n.d. | n.d. | n.d. | n.d. |
| 8 | Bôrčianska | 4.0 | 0.0457 | 2864 | 2.54 | 0.0067 |
| 9 | Zádielska | 4.9 | 0.0503 | 20,344 | 2.59 | 0.0764 |
| 10 | Jasovská | 4.9 | 0.0622 | 14,158 | 2.76 | 0.0456 |
| 11 | Kečovská-Haragistya | 6.9 | 0.0877 | 27,436 | 2.12 | 0.4330 |
| 12 | Nagyoldal | 7.1 | 0.0956 | 21,483 | 2.08 | 0.5010 |
| 13 | W-Alsó-hegy | 5.9 | 0.0846 | 17,456 | 2.00 | 0.2707 |
| 14 | E-Alsó-hegy | 10.0 | 0.1384 | 26,113 | 2.25 | 0.7828 |
| 15 | Szinpetri | 7.4 | 0.0840 | 36,645 | 1.97 | 0.3987 |
| 16 | Páska-bükk | 12.4 | 0.1052 | 139,720 | 2.05 | 1.5124 |
| 17 | Aggtelek | 8.4 | 0.0835 | 66,745 | 2.04 | 0.5856 |
| 18 | Rudabánya | 1.0 | 0.0257 | n.d. | n.d. | n.d. |
| 19 | Szalonna | 8.5 | 0.0885 | n.d. | n.d. | n.d. |
| 20 | Jósvafő | 4.2 | 0.0571 | 14,796 | 1.90 | 0.4890 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Telbisz, T.; Mari, L.; Székely, B. LiDAR-Based Morphometry of Dolines in Aggtelek Karst (Hungary) and Slovak Karst (Slovakia). Remote Sens. 2024, 16, 737. https://doi.org/10.3390/rs16050737
Telbisz T, Mari L, Székely B. LiDAR-Based Morphometry of Dolines in Aggtelek Karst (Hungary) and Slovak Karst (Slovakia). Remote Sensing. 2024; 16(5):737. https://doi.org/10.3390/rs16050737
Chicago/Turabian StyleTelbisz, Tamás, László Mari, and Balázs Székely. 2024. "LiDAR-Based Morphometry of Dolines in Aggtelek Karst (Hungary) and Slovak Karst (Slovakia)" Remote Sensing 16, no. 5: 737. https://doi.org/10.3390/rs16050737
APA StyleTelbisz, T., Mari, L., & Székely, B. (2024). LiDAR-Based Morphometry of Dolines in Aggtelek Karst (Hungary) and Slovak Karst (Slovakia). Remote Sensing, 16(5), 737. https://doi.org/10.3390/rs16050737