As the main body of the terrestrial ecosystem and the largest organic carbon reservoir [
1,
2], forests play an irreplaceable role in regulating the global carbon cycle [
3] and mitigating the global climate change crisis [
4]. However, accurate inversion of forest above ground biomass (AGB) remains challenging, especially in regions with complex topography, which greatly limits sustainable mountain forest stand management and the quantification of carbon sequestration by AGB [
5,
6]. Synthetic aperture radar (SAR) is an advanced remote sensing observation technology for the earth, and because of its active remote sensing and microwave penetration characteristics, it has all-time, all-weather working capability [
7,
8]. Therefore, it can effectively avoid the problems of time-consuming and labor-intensive discontinuity in ground measurement [
9,
10], the problems of optical remote sensing being easily restricted by climate factors and the bottleneck of saturation point [
11,
12,
13], and the limitations of light detection and ranging (LiDAR) remote sensing being limited in scale and high in economic cost [
14], which are conducive to long-term, continuous, and macroscopic observation of large areas. However, as SAR is a side-looking radar imaging system that judges oblique distance based on echo time, SAR data are not only affected by system parameters (wavelength, radar incidence angle, polarization mode) but also limited by surface characteristics (complex dielectric constant, terrain slope, surface roughness). The topographic factor interferes with SAR data especially seriously, and the geometric deformation and radiation distortion caused by it lead to the serious deviation of the backscattering coefficient of ground objects [
15], thus restricting the reliability of forest AGB inversion based on the backscattering coefficient of SAR images. Therefore, it is very important to explore the technique of retrieving AGB in mountainous forest areas with complex terrain based on the SAR dataset. Since different AGB inversion schemes have different topographic correction processes, the inversion technology of aboveground biomass is first analyzed. At present, AGB estimation techniques based on SAR data can be divided into: (1) Statistical modeling method based on SAR characteristic parameters (including backscattering coefficient [
16,
17,
18,
19], polarization decomposition parameter [
20,
21], interference coherence [
22,
23,
24], and tomographic vertical structure parameter [
25]) and (2) forest canopy height extracted from interferometric SAR (InSAR) [
26,
27,
28], polarimetric interferometric SAR (PolInSAR) [
29,
30,
31] and tomographic SAR (TomoSAR) [
32]; and then indirect AGB estimation using an allometric equation [
33,
34]. Among them, the accuracy of indirect inversion of forest AGB based on an allometric equation is heavily dependent on the inversion accuracy of the growth equation and forest canopy height. However, the accurate acquisition of forest height, interference coherence, and tomographic vertical structure parameters depends on InSAR, PolInSAR, TomoSAR, and other related technologies, which are mostly used for airborne data but seldom studied for spaceborne data, are not mature enough, and have many limitations. However, polarimetric SAR (PolSAR) technology can obtain multi-polarization scattering information about ground objects, so it has been widely used in estimating forest AGB [
35,
36,
37]. In addition, the forest AGB model constructed based on SAR characteristic parameters is divided into a parametric model and a non-parametric model, among which the non-parametric model has greater flexibility and adaptability because it does not depend on specific functional forms [
38,
39]. However, the parameter model is easy to explain and understand because of its clear mathematical formula, and the parameter estimation can be relatively fast and the calculation efficiency is high, so it has a wide range of applications in the estimation of forest AGB. The method of retrieving AGB based on the backscattering coefficient of PolSAR data is relatively mature and widely used, so this study focuses on analyzing the influence of terrain on the parameter model based on the backscattering coefficient to retrieve AGB. For full-polarization SAR data, the backscattering coefficient method is to extract the backscattering intensity of different polarization channels after proper preprocessing of PolSAR data and establish a univariate or multivariate statistical model about AGB [
40]. However, PolSAR data are affected by topographic factors, resulting in geometric deformation and radiation distortion of SAR images [
41]. Among them, the correction of geometric distortions (including foreshortening, layover, and shadow) can be done during geocoding of terrain correction (GTC) [
42]. In addition, the impact of topographic factors on radiation distortion of PolSAR data mainly includes three aspects [
43]: (1) The shift of polarization orientation angle (POA) results in a change in polarization state; (2) the difference in effective scattering area (ESA) leads to a change in intensity information of target scattering matrix elements; (3) changes in the scattering mechanism and penetration depth are caused by the angular variation effect (AVE). For sloping ground, the POA will shift [
44]. As the parameters of the polarization elliptic equation, POA and ellipse angle can be used to describe the polarization state of any polarized electromagnetic wave [
45]. Therefore, the polarization state of a polarized electromagnetic wave will change correspondingly with the change in POA. As the key to polarization orientation angle correction (POAC), the extraction of POA currently has four methods: Based on the polarization response method [
46], based on polarization decomposition method [
47], based on the external DEM method [
48], and based on the circular polarization covariance matrix method [
48]. Among them, the estimation method based on circular polarization covariance matrix has the best adaptability, a simple calculation process, and an optimal comprehensive effect [
49]. Subsequently, correction factors constructed by POA are used to compensate for different forms of polarization information [
48,
50,
51], such as the complex Sinclair scatter matrix (S2), the three-dimensional polarization coherency matrix (T3), or the three-dimensional polarization covariance matrix (C3). It is worth noting that the compensation for POA is only for full-polarization SAR data [
48]. Effective scattering area correction (ESAC) is a system-level correction of the SAR image based on the geometric relationship of the SAR image and is a necessary step in radiation terrain correction. For ground units with only different slopes (even with geometric correction), the existence of a topographic slope will lead to differences in the projected area (effective scattered echo information) of their positive plane; for example, the echo intensity of the front slope is greater than that of the back slope [
43]. At present, there are four ESAC methods: Local incidence angle method [
52,
53] and projection angle method [
54] under ground distance geometry, and
σ area integration method and
γ area integration method under oblique distance geometry [
55,
56], which can correct PolSAR information such as backscattering coefficient or C3 or T3. Angular variation effect correction (AVEC) takes into account factors such as the penetration depth of radar waves and the interaction mechanism between the radar waves and vegetation, which is a more precise correction method for vegetation areas with certain penetration. Therefore, for forested areas, further AVEC is required on the basis of ESAC. AVEC usually uses the semi-empirical correction equation of the cosine of the local incidence angle to the
nth power [
57], where the
n value depends on the polarization mode and the structural characteristics of the vegetation canopy and is usually given based on prior knowledge. Subsequently, a variety of methods for the value of
n have appeared [
52,
57,
58,
59,
60], but they are still difficult to apply because they cannot be separated from prior knowledge. However, a new iterative method [
43] based on the minimum correlation coefficient between the backscattering coefficient and the local incidence angle after AVEC realizes the adaptive determination of the optimal
n value for different polarized channels.
Compared to a process that does not consider or does not adequately consider topographic correction [
38,
61], radiative terrain correction for PolSAR data is a combination of three aspects of terrain correction [
50,
59,
60,
62,
63], of which the most comprehensive radiometric terrain correction (RTC) process is one that includes all three aspects (POAC, ESAC, and AVEC) [
43,
64,
65]. However, in terms of ESAC, the cross-sectional area of radar scattering is only applicable to a single scattering target (the target object is smaller than the irradiation range), and the scattered signal of the resolution unit for distributed scatterers (such as forests) is the result of coherent superposition of the scattered signal of each single scatterer, so the backscattering coefficient is commonly used to describe the scattering ability of ground objects based on statistical methods. Three different backscattering coefficients can be defined according to the area of the effective scattering element: The backscattering coefficient of the imaging surface (
β0), the backscattering coefficient of the ground regardless of the terrain (
σ0), and the backscattering coefficient of the isophase surface (
γ0) [
55,
66]. When ESAC’s object is
σ0, it essentially converts
σ0 to
γ0 in relation to the topographic factor. However, when the ESAC object is C3 or T3, it is not appropriate to directly use the ESAC factors applied to
σ0 as the ESAC factors of C3. Because, on flat ground with no topographic slope, C3 does not require topographic correction; that is, the correction factor should equal 1.0. Therefore, it is necessary to introduce a new ESAC factor to realize real terrain correction rather than simple conversion. In addition, the robustness of the RTC process to different AGB inversion models and different SAR data has not been fully evaluated.
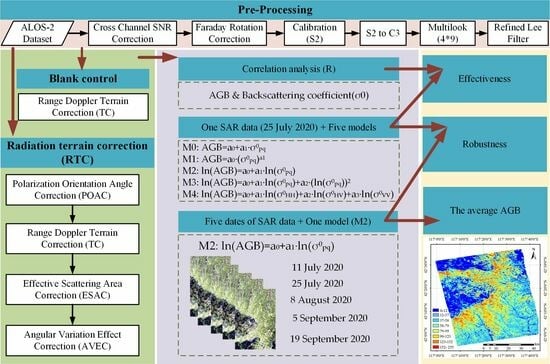
This study aims to achieve three goals: (1) In order to deal with the problem that the impact of terrain on SAR data is not considered or not fully considered, we fully consider the impact (including POA, ESA, and AVE) of terrain on PolSAR data in AGB inversion based on the backscattering coefficient method; (2) to solve the problem that PolSAR data needs more accurate terrain correction rather than simple conversion, we introduced and verified the effectiveness of the ESAC normalized correction factor; and (3) to evaluate the robustness of the RTC process under different AGB models and SAR data of different dates, because it has not been adequately evaluated.