Next Article in Journal
Autonomous Navigation Airborne Forward-Looking SAR High Precision Imaging with Combination of Pseudo-Polar Formatting and Overlapped Sub-Aperture Algorithm
Next Article in Special Issue
Combined Spatial and Temporal Effects of Environmental Controls on Long-Term Monthly NDVI in the Southern Africa Savanna
Previous Article in Journal
Exploring the Use of Google Earth Imagery and Object-Based Methods in Land Use/Cover Mapping
Previous Article in Special Issue
Evaluation of Land Surface Models in Reproducing Satellite-Derived LAI over the High-Latitude Northern Hemisphere. Part I: Uncoupled DGVMs
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 5
Issue 11
10.3390/rs5116043
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Recent Changes in Terrestrial Gross Primary Productivity in Asia from 1982 to 2011

by
Kazuhito Ichii
1,2,*,
Masayuki Kondo
1,
Yuki Okabe
1,
Masahito Ueyama
3,
Hideki Kobayashi
4,
Seung-Jae Lee
5,
Nobuko Saigusa
2,
Zaichun Zhu
6,7,8 and
Ranga B. Myneni
8
1
Faculty of Symbiotic Systems Science, Fukushima University, Kanayagawa, Fukushima 960-1296, Japan
2
Center for Global Environmental Research, National Institute for Environmental Studies, 16–2, Onogawa, Tsukuba 305-8506, Japan
3
Graduate School of Life and Environmental Sciences, Osaka Prefecture University, 1–1, Gakuen-cho, Naka-ku, Sakai 599-8531, Japan
4
Research Institute for Global Change, Japan Agency for Marine-Earth Science and Technology, 3173-25, Showa-machi, Kanazawa-ku, Yokohama 236-0001, Japan
5
National Center for Agro-Meteorology, Seoul National University, Gwanak-ro, Gwanak-gu, Seoul 151-921, Korea
6
State Key Laboratory of Remote Sensing Science, Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China
7
Center for Applications of Spatial Information Technologies in Public Health, Beijing 100101, China
8
Department of Earth and Environment, Boston University, 685 Commonwealth Avenue, Boston, MA 02215, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2013, 5(11), 6043-6062; https://doi.org/10.3390/rs5116043
Submission received: 30 September 2013 / Revised: 25 October 2013 / Accepted: 11 November 2013 / Published: 15 November 2013
(This article belongs to the Special Issue Monitoring Global Vegetation with AVHRR NDVI3g Data (1981-2011))
Browse Figures
Versions Notes

Abstract

:
Past changes in gross primary productivity (GPP) were assessed using historical satellite observations based on the Normalized Difference Vegetation Index (NDVI) from the Advanced Very High Resolution Radiometer (AVHRR) onboard the National Oceanic and Atmospheric Administration (NOAA) satellite series and four terrestrial biosphere models to identify the trends and driving mechanisms related to GPP and NDVI in Asia. A satellite-based time-series data analysis showed that approximately 40% of the area has experienced a significant increase in the NDVI, while only a few areas have experienced a significant decreasing trend over the last 30 years. The increases in the NDVI are dominant in the sub-continental regions of Siberia, East Asia, and India. Simulations using the terrestrial biosphere models also showed significant increases in GPP, similar to the results for the NDVI, in boreal and temperate regions. A modeled sensitivity analysis showed that the increases in GPP are explained by increased temperature and precipitation in Siberia. Precipitation, solar radiation and CO2 fertilization are important factors in the tropical regions. However, the relative contributions of each factor to GPP changes are different among the models.

Graphical Abstract

1. Introduction

Asia, which is characterized by a rapidly growing economy, human-induced disturbances, and climate changes, is an important region for understanding global terrestrial carbon cycles [1–3]. Siberian regions have experienced a 1.0–2.0 °C increase in temperature from 1961 to 2004 [4]. China and India have recently experienced rapid economic growth and a large increase in CO2 emissions. For example, CO2 emissions in China and India accounted for 28% and 7%, respectively, of the global CO2 emissions in 2011 [5]. In addition, many regions, for example, China, Southeast Asia, and South Asia, have experienced land-use changes, including changes in the use of cropland and forest areas [6,7].
Terrestrial gross primary productivity (GPP) is the largest atmosphere-land carbon flux, driving terrestrial carbon cycles as a primary input for vegetation carbon. An accurate estimate of the magnitude of temporal GPP changes is required to quantify and predict terrestrial carbon budgets. Numerous approaches have been used to analyze GPP at both global and regional scales, which include analyzing satellite-based remote sensing data as an indicator of GPP [8–11], using empirical upscaling with machine learning techniques [12–15], and assembling diagnostic [16–18] and prognostic [19,20] terrestrial biosphere model simulations.
These approaches have also been used to analyze spatio-temporal GPP variations in Asia. For example, numerous studies have analyzed satellite-based time-series data, including data that from the Advanced Very High Resolution Radiometer (AVHRR) onboard the National Oceanic and Atmospheric Administration (NOAA) satellite series, to infer GPP variations in relation to environmental changes. Analyses of NOAA AVHRR data have revealed that vegetation productivity is increasing and the growing season has lengthened in boreal and Arctic regions [8,9,21]. In East Asia, including China, several studies have revealed that the vegetation greenness has increased over the last 20–30 years [22–26]. In Southeast Asia, interannual variations in vegetation indices were found to be largely determined by the El Niño Southern Oscillation [27]. Furthermore, vegetation greenness was found to have increased in India because irrigated areas and fertilization use increased [28]. However, this increase in vegetation greenness has stagnated in recent years [29]. Terrestrial biosphere models and empirical models have also been used to analyze GPP variations in many regions in Asia. Empirically upscaled estimates of GPP in East Asia revealed a significant reduction in the summer of 2003 in response to meteorological anomalies [30]. Increased GPP has also been identified using diagnostic terrestrial biosphere models in China [31] and India [28].
Further analyses could utilize a combined application of satellite-based observations and terrestrial biosphere models. Moreover, satellite-based observation data can be used for model evaluation. Once the model output successfully reproduces the satellite-based observations, mechanisms from the observed results can be analyzed with process-based models using sensitivity experiments. Recent vegetation greening trends in northern high-latitude regions have been analyzed using the satellite-based leaf area index (LAI) and a terrestrial biosphere model; increases in temperature were related to the vegetation greening trend [32]. The combined use of remote sensing data and terrestrial biosphere models have helped explain the observed changes in the Normalized Difference Vegetation Index (NDVI) in the Amazon from 1984 to 1999. In this region, increased solar radiation has been found to enhance the terrestrial net primary productivity [33]. Vegetation growth in the Northern Hemisphere (>25°N) has been explained by a process-based terrestrial biosphere model and has been found to have resulted from changes in atmospheric CO2, temperature, and precipitation [34]. An application of the above approaches to Asian regions could elucidate the changes in vegetation greening trends in Asia in a process-based manner.
In this study, we used both satellite-based time-series observations and four process-based terrestrial biosphere models to identify and understand changes in terrestrial GPP in Asia (the regions are defined in Figure 1). Using the updated satellite-based vegetation index products, that is, NOAA AVHRR NDVI3g [37,38], we first quantified changes in the NDVI from 1982 to 2011 in Asia and identified the regions with increasing or decreasing trends in vegetation activity. Then, we applied four different terrestrial biosphere models to simulate recent changes in terrestrial GPP; we verified these results with satellite-based NDVI variations as a proxy of terrestrial GPP at sub-continental scales. Finally, using the model simulation results, we determined the causes of the simulated trends in terrestrial GPP.

2. Materials and Methods

2.1. Study Region

We analyzed a region that covers a wide range of vegetation and climate conditions in Asia (Figure 1a), including a temperature gradient from tropical forest regions in Southeast Asia (annual average temperature > 25 °C) to tundra regions in Siberia (annual average temperature < −10 °C) as well as a precipitation gradient from coastal and tropical regions (>2,000 mm·year−1) to semiarid or arid regions in Central Asia (<200 mm·year−1). The vegetation cover also exhibits large differences with evergreen tropical forests in Southeast Asia; temperate forests in East Asia; boreal forests in Siberia; croplands in China, India and Russia; grasslands in central Asia; and open shrublands (tundra) in northern Siberia.
For a sub-continental scale analysis, we divided the region into nine sub-regions based on the definition used in the atmospheric CO2 inversion analysis (Figure 1b). We adopted the sub-continental division of the Greenhouse Gases Observing Satellite (GOSAT) Level 4A products (i.e., CO2 flux for each of the 64 global regions) [36]. The areal definition is based on the continental-scale vegetation type. Therefore, this sub-region definition is suitable for assessing the large-scale terrestrial carbon cycle changes in specific ecosystems at the sub-continental scale.

2.2. Data

2.2.1. Satellite-Based Time-Series Data: NDVI, LAI, and FPAR

The latest version of the NDVI dataset generated from the AVHRR sensor onboard a series of NOAA satellites (Global Inventory Modeling and Mapping Studies (GIMMS) NDVI3g) from January 1982 to December 2011 was used in this study [37,38]. The NDVI data were used as a proxy for terrestrial GPP [39] to compare with the model outputs. The datasets were provided with a spatial resolution of 8 km × 8 km and a 15-day temporal resolution over the period from July 1981 to December 2011. To create spatially and temporally consistent data with the terrestrial biosphere model simulations, we averaged the GIMMS NDVI3g data to create quarter-degree spatial resolution and monthly temporal resolution data.
The third generation data of the LAI and Fraction of Photosynthetically Active Radiation absorbed by a canopy (FPAR) datasets (LAI3g and FPAR3g) [40] were used as inputs for the BEAMS model [18,41]. These datasets are integrated products of GIMMS NDVI3g data [37,38] and Moderate Resolution Imaging Spectroradiometer (MODIS) LAI/FPAR products [42] that include updated algorithms for data screening [43]. In generating the LAI3g and FPAR3g data, a set of neural networks were first trained on best-quality and post-processed MODIS LAI and FPAR products as well as GIMMS NDVI3g data for the overlapping period from 2000 to 2009. The trained neural networks were then used to produce the LAI3g and FPAR3g datasets using GIMMS NDVI3g data for the remaining period. The original data were provided at 15-day temporal intervals and 8-km spatial resolutions. We converted these data into monthly temporal resolution and quarter-degree spatial resolution by averaging that data using the same procedure used for the NDVI dataset.

2.2.2. Climate Time-Series Data

Daily climate data were generated from 1901 to 2011 with quarter-degree spatial resolution by merging reanalysis-based products and observation-based products based on a similar approach used with the CRUNCEP data [44]. For example, daily air temperature data from 1901 to 2011 were generated based on the Climate Research Unit Time Series 3.2 (CRU TS3.2) data (available period: 1901–2011) [45] and National Centers for Environmental Prediction (NCEP)/the National Center for Atmospheric Research (NCAR) reanalysis (NCEP/NCAR reanalysis) data (available period: 1948 to present) [46]. The daily variations in air temperature were based on NCEP/NCAR reanalysis data; the monthly averages were adjusted to fit the CRU TS3.2 data by adding an offset. Because NCEP/NCAR reanalysis data are not available for the 1901–1947 period, the reanalysis data for 1948 were used instead. Similarly, precipitation data were generated by merging daily NCEP/NCAR reanalysis data and CRU TS3.2 monthly precipitation data [45] by multiplying by an adjustment factor. In addition, we found that the frequency of rainy days in the NCEP/NCAR reanalysis data was too high compared with the CRU TS3.2 wet-day frequency data. Therefore, the frequency of wet days was also adjusted using the CRU TS3.2 wet-day frequency data by redistributing the rain. Incoming surface shortwave radiation data were generated by merging daily shortwave radiation created by the Mountain Climate Simulator (MTCLIM) [47] (available period: 1901–2011) and monthly averages of Japan Aerospace Exploration Agency (JAXA) NASA/MODIS global 5-km irradiance (JAXA radiation) data [30,48] (available period: 2000–2010) by multiplying by an adjustment factor. The MTCLIM-based shortwave radiation relies on the assumption that variations in diurnal temperature ranges are related to incoming solar radiation. Because JAXA radiation data are not available for 1901–1999 and 2011, the average of the data for 2000–2010 was used instead. Daily vapor pressure deficit data were generated using MTCLIM. For longwave radiation and wind speed, NCEP/NCAR reanalysis data were directly used; the data from 1948 were used for the 1901–1947 period.

2.2.3. Atmospheric CO2 Time-Series Data

Atmospheric CO2 data were obtained from the observed monthly mean at the Mauna Loa station from 1959 to 2011 [49] and from the observed annual mean from the ice core at Law Dome, Antarctica, from 1901 to 1958 [50]. The monthly mean atmospheric CO2 concentration data from 1901 to 1958 were created by subtracting differences in the annual mean between 1959 and the corresponding year from the monthly data in 1959. The annual mean atmospheric CO2 concentrations were used as inputs to the Biome-BGC, LPJ and TRIFFID models. The monthly mean atmospheric CO2 concentrations were used as model inputs for BEAMS.

2.2.4. Static Data

Static data used for the analysis included land cover, elevation, soil texture, and soil depth. Land-cover data were derived from MODIS products (MCD12Q1 collection 5.0) [35] by taking the most dominant land cover in each quarter-degree grid cell. Elevation data were obtained from GTOPO30 [51]. Soil texture data and soil depth data were created using the Harmonized World Soil Database version 1.2 and ISLSCP II Ecosystem Rooting Depths (mean 95% ecosystem rooting depth in meters [52]), respectively. All data were re-gridded to quarter-degree resolution using the nearest neighbor method.

2.3. Terrestrial Biosphere Models

We used four terrestrial biosphere models to analyze changes in GPP from 1982 to 2011. The models included BEAMS Version 1.3 [18,41], Biome-BGC Version 4.2 [53], LPJ Version 3 [20,54], and MOSES/TRIFFID [55,56]. These models differ in terms of their model structure, parameters, and required input data. The BEAMS model is categorized as a diagnostic terrestrial biosphere model, which simulates spatial and temporal patterns in the carbon cycle more realistically using satellite-based LAI and FPAR inputs than prognostic terrestrial biosphere models. The model calculates GPP using a function of FPAR, shortwave radiation and an environmental regulation factor. The environmental regulation factor is calculated by combined Farquhar’s photosynthesis model [57,58] and the Ball-Berry-type stomatal conductance model [59,60] using CO2, temperature, soil moisture, and relative humidity. The Biome-BGC model is a prognostic terrestrial biosphere model with fixed vegetation cover. The model runs with only climate data as a time-variant input. The model calculates GPP using a function of the CO2, shortwave radiation, temperature, soil moisture, and vapor pressure deficit using the Farquhar biochemical photosynthesis model [57] with a Jarvis-type stomatal conductance model [61]. LPJ and TRIFFID are dynamic global vegetation models that explicitly simulate vegetation types and run with only climate data as a time-variant input. The LPJ model calculates GPP using a function of CO2, shortwave radiation, temperature, and soil moisture using the Farquhar biochemical photosynthesis model [62] with stomatal conductance estimated from a Ball-type conductance model [59]. The TRIFFID model calculates GPP as a function of CO2, shortwave radiation, temperature, soil moisture, and relative humidity using a leaf-level photosynthesis model [58,63] with a coupled photosynthesis and stomatal conductance model [64].
The models were used under a consistent protocol. The 1901–1930 period was used for the spin-up period dependent on each model’s spin-up setting. The models were run from 1901 to 2011 with time-variable inputs of climate data (for all models) and satellite-based LAI and FPAR data (for BEAMS only). BEAMS was spun-up for 3000 years using 1901 climate data. Biome-BGC was spun-up using the 1901–1930 climate data repeatedly until the soil carbon reached equilibrium, with 6,000 years as the maximum spin-up length. LPJ was spun-up for 1,000 years using the 1901–1930 climate data repeatedly with the fire module disabled. Finally, TRIFFID was spun-up for 1000 years using the 1901–1930 climate data repeatedly.
In addition to the simulations with time-variable inputs for all climate parameters, we conducted sensitivity experiments based on an existing study to identify the causes of temporal GPP variations [65]. For each simulation, the models were run using only one climate time-series with an interannual variability in temperature, precipitation, solar radiation and atmospheric CO2 concentration; the other climate components were held at their 1901 values. We tested four climate parameters (i.e., temperature, precipitation, solar radiation and atmospheric CO2 concentration) that are commonly incorporated in terrestrial biosphere models.

2.4. Analysis

2.4.1. Detection of the NDVI and Climate Trends from 1982 to 2011

Using the NDVI data from 1982 to 2011, trends in the NDVI were estimated in each grid and each subcontinental region in a manner similar to an existing study [33]. The Mann-Kendall trend test [66] was used for statistical analysis because this technique does not require an assumption of normality in variance and is more robust against anomalous outliers compared with linear regression analysis. The slopes of the trends were calculated based on the Kendall robust line-fit method [67], which is a method for robust linear regression that chooses the median slope among all lines through pairs of two-dimensional sample points. The method is a non-parametric method and is relatively insensitive to outliers.
To avoid including changes in non-vegetation effects (e.g., snow) in the calculation of temporal changes, we focused on the annual average during the vegetation growing season in each grid cell. The vegetation growing season is defined in each grid as those months in which the 1982–2011 monthly average air temperatures were greater than 5 °C and the monthly average NDVI was greater than 0.1.
Climate trends (temperature and precipitation) were also estimated from 1982 to 2011 to interpret the NDVI trends using the same approach as for the NDVI analysis, that is, the Kendall robust line-fit method [62]. We used the growing season average for temperature and the annual total for precipitation in the trend estimation.

2.4.2. Evaluation of Trends in NDVI and Modeled GPP from 1982 to 2011

Recent trends in GPP from 1982 to 2011 were analyzed using model simulation results with time-variable inputs. Changing trends in the annual total GPP, which were estimated using the same methods as described in Section 2.4.1, were compared with satellite-based NDVI trends. Furthermore, we also evaluated the interannual variations in the NDVI and modeled GPP based on the correlation analysis between the NDVI and modeled GPP using Kendall’s rank correlation coefficients (Kendall’s τ) [66] to determine the ability of each model to simulate interannual variability consistently with the satellite-based NDVI.

2.4.3. Attribution of the Detected Changes in NDVI and GPP

Factors determining the modeled GPP trends were analyzed using the results of sensitivity experiments for each terrestrial biosphere model. A series of model simulations was conducted by changing a single time-series climate variable—temperature, precipitation, solar radiation, or atmospheric CO2 concentration—while keeping the other climate variables fixed. To ensure that the comparison was consistent among the models, we used outputs from three terrestrial biosphere models that can only be run with climate data (i.e., Biome-BGC, LPJ and TRIFFID). The BEAMS model was not used in this analysis because the model uses time-variable satellite-based LAI and FPAR, which already contains climate variation effects, and isolating the unique effect of a specific climate parameter is difficult.
We evaluated the relative contribution of each individual factor—that is, temperature, precipitation, solar radiation, and atmospheric CO2 concentration—to the simulated GPP trends under actual climate variations. Using the model results simulated by changing a single time-series climate variable, we evaluated the relative contribution of each individual factor by plotting them in stacked bar graphs in each region and for each model.

3. Results and Discussion

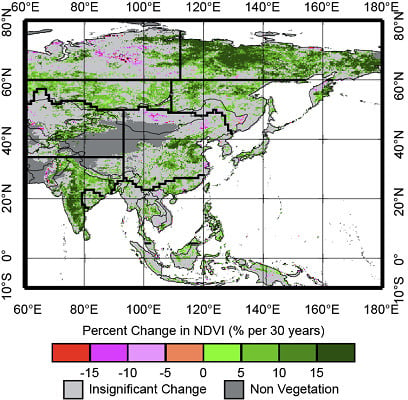
3.1. Observed Climate and NDVI Trend for 1982–2011

For the 1982–2011 period, the temperature increased over most regions; precipitation had a geographically variable pattern in the sign of the trends (Figure 2). Distinct increases in temperature were distributed over eastern Siberia (60°N–75°N, 110°E–180°E) and semiarid regions around inner-Mongolia (45°N–50°N, 100°E–130°E). Precipitation had distinct increases in eastern Siberia (60°N–75°N, 110°E–180°E) and part of India (10°N–25°N, 70°E–80°E), with distinct decreases in semiarid regions around inner-Mongolia (45°N–50°N, 100°E–130°E).
Increasing trends in the NDVI were dominant in Asia for the 1982–2011 period (Figure 3). Moreover, 41.8% of the vegetated regions had increased NDVI values, with distinct increases in eastern Siberia (50°N–80°N, 100°E–180°E), boreal Eurasia (45°N–60°N zones), parts of China and India, and some scattered regions in tropical Asia. However, the regions with significant NDVI decreases were distributed among small regions (2.9% of the vegetated regions); for example, parts of western Arctic Siberia (60°N–80°N, 80°E–100°E) and semiarid regions around inner-Mongolia (45°N–50°N, 100°E–120°E).
In the sub-continental scale analysis, we detected a statistically significant NDVI increase in seven of the nine sub-continental regions (Table 1). The two exceptions were the Boreal Eurasia North West region and the Tropical Asia South region. However, these regions had positive but minor increases in the NDVI. In the Boreal Eurasia North West region, interannual variations in the NDVI gradually increased from 1982 to 2000 and decreased after 2001, except for 2011 (Figure 4a). In the Tropical Asia South region, the NDVI had large interannual variations without significant increasing or decreasing trends from 1982 to 2000 (Figure 4i).

3.2. Evaluation of the 30-Year Trends in NDVI and Modeled GPP

The terrestrial biosphere models suggest increasing GPP in Asia from 1982 to 2011, which is mostly consistent with the satellite-based NDVI trends. The Biome-BGC and LPJ models exhibited significant increasing GPP trends in all nine regions. Moreover, the BEAMS and TRIFFID models showed significant increasing GPP trends in eight regions (Table 1). The consistency between models and the NDVI is highest for the BEAMS model because the model uses satellite-based LAI and FPAR as inputs; only the Tropical Asia South region did not exhibit a difference in the trend significance (e.g., the BEAMS model predicts statistically significant increases in GPP, whereas the NDVI does not) likely due to uncertainties in the solar radiation data used for BEAMS models. In both the Boreal Eurasia North West region and the Tropical Asia South region, the prognostic terrestrial biosphere models (Biome-BGC, LPJ, and TRIFFID) suggest significant increases in GPP. However, a similar trend is not detected for the NDVI.
The interannual variations in the NDVI and modeled GPP were highly consistent in temperate and boreal regions and weakly consistent in tropical regions (Table 2 and Figure 4). We found that the BEAMS-based GPP, in which GPP was calculated using satellite-based LAI and FPAR data, was highly consistent with the satellite-based NDVI (e.g., τ = 0.67 – 0.83 for boreal and temperate regions). The results from the prognostic biosphere models also showed good agreement with the satellite-based NDVI data regarding interannual variations in GPP (e.g., averages of τ in all boreal and temperate regions are τ = 0.48, 0.50 and 0.43 for Biome-BGC, LPJ, and TRIFFID, respectively). However, we found large deviations between the models and the satellite-based NDVI in tropical forest regions (e.g., τ < 0.3 for most tropical regions).
The consistency of interannual variability and 30-year trends in boreal and temperate regions between the NDVI and modeled GPP indicates that these increases are robust for the different methodologies, that is, terrestrial biosphere models and satellite-based observations. Therefore, we can use the models to perform a process-based analysis on the underlying mechanisms. As exceptions, disagreement between the model and the NDVI data was detected in several regions and specific years. For example, in the Boreal Eurasia North West region, mainly during the 2007–2010 period (Figure 4a), the satellite-based NDVI had negative anomalies for this period, whereas the GPPs in the prognostic models (Biome-BGC, LPJ, and TRIFFID) had positive anomalies for this period. Another distinct difference was found in the Temperate Asia North West over the period 1996–2001. In this region, there was a consistent discrepancy between the three model simulations run with only climate data (i.e., BIOME-BGC, LPJ and TRIFFID) versus the NDVI data and the BEAMS model simulation that incorporates effects of satellite-based observation. In addition, the BIOME-BGC simulations had anomalously high spikes in 2007 for all temperate regions. The disagreement between these data should be analyzed in the future to identify the potential limitations of each methodology.
Disagreements between the models and data for tropical regions are evident in the current study. Possible explanations may relate to both the satellite-based observations and the terrestrial biosphere models. In principle, monitoring tropical forests using shortwave radiations from satellite-based observations is difficult because of atmospheric effects, for example, severe cloud contamination and heavy aerosol loading in tropical regions [68]. Moreover, simulating the terrestrial carbon cycle using terrestrial biosphere models is difficult in tropical forests. For example, a site-level model comparison study showed that the model performance in simulating carbon fluxes was poor in tropical forests among various ecosystems in Asia [69]. The difficulty in modeling GPP in tropical forest is partly due to complex processes involving water and solar radiation controls on seasonal GPP variations and the requirement for appropriate rooting depth settings [70].

3.3. Attribution of Detected Changes in NDVI and GPP

In boreal Eurasia regions (the Boreal Eurasia North West, North East, South West and South East regions), the modeled increases in GPP are explained by variations in temperature (Biome-BGC and LPJ models), precipitation (Biome-BGC, LPJ, and TRIFFID models), and atmospheric CO2 concentration (LPJ and TRIFFID models) (Figure 5a–d). Changes in temperature and precipitation provide similar contributions to the GPP increase. The Biome-BGC model showed that increases in the atmospheric CO2 concentration had a small effect on the GPP increase. However, the LPJ and TRIFFID models showed that changes in atmospheric CO2 concentration, temperature, and precipitation had similar effects on GPP.
In the temperate Asia regions (the Temperate Asia North West, North East and South East regions), the causes of the GPP increases were not consistent among the models (Figure 5e–g). The GPP increases were primarily due to changes in temperature in the Biome-BGC model. According to the LPJ and TRIFFID models, atmospheric CO2 concentration change is the main driver of the GPP increases.
In tropical Asia (the Tropical Asia North and South regions), the GPP increases were mostly explained by changes in atmospheric CO2 concentration in the LPJ and TRIFFID models. In the Biome-BGC model, changes in precipitation and the atmospheric CO2 concentration equally contributed to the increases in GPP. Changes in incoming solar radiation were another important factor in the GPP increases in the Tropical Asia South region in the Biome-BGC and LPJ models. However, quantifying the solar radiation contribution requires better estimates of solar radiation (see Section 3.4).
Although the estimated GPP trends were similar for the different models and were generally consistent with the satellite-based NDVI trends, the contribution of CO2 fertilization to the increase in GPP differed among the models and regions (Figure 5). The CO2 fertilization effect on the GPP trends was lower in the Biome-BGC model compared with the LPJ and TRIFFID models. Therefore, further analysis using data from field observations [71] is required to elucidate the effects of CO2 fertilization on GPP.

3.4. Limitations and Potential Further Studies

Based on the analysis of the four terrestrial biosphere models and the satellite-based NDVI data, we found that the detected NDVI trends are mostly consistent with model-based GPP trends in Asia. These detected NDVI and GPP trends were analyzed to identify the important processes driving changes in the NDVI and GPP using the terrestrial biosphere models.
To fill the gaps in the results from the satellite-based NDVI and model-based GPP, additional analyses are required. First, the terrestrial biosphere models need to be further improved to reproduce observed carbon fluxes in Asia [69,72] and other regions, for example, North America [73] and Europe [74]. Further refinements to these models using ground-based observation networks [75] may improve the consistency between the modeled GPP and the satellite-based NDVI and inter-model consistency. Second, an analysis of human-induced disturbances and land-use changes, including afforestation and agriculture, should be assessed in future studies because afforestation in China [22] and the increased irrigation area and fertilization use in India [28] have been found to contribute to increases in terrestrial GPP and the NDVI. In addition, the terrestrial biosphere models used in this study do not include disturbance effects or land-use changes, including plantation and deforestation in the tropical Asia. Third, to assess each model’s sensitivity to climate anomalies, terrestrial GPP anomalies in response to certain anomalous climate events should be analyzed. For example, the Boreal Eurasia South East region experienced cooler and cloudier meteorological conditions in the summer of 2003, corresponding to negative anomalies in GPP. All of the models showed the same negative GPP anomalies in 2003 (Figure 4d). The mechanisms should be carefully assessed using observations and models to determine if each model reproduces GPP anomalies through a similar mechanism. Fourth, a further assessment of model-data mismatches should be conducted to clarify the potential issues for both models and satellite-based observations. In this study, we demonstrated several model and data mismatches in Section 3.2. Identifying the mismatch causes may improve the performances of terrestrial biosphere models.
A quantitative comparison of the models and data are also required in the further studies even though current qualitative assessments showed consistent variations in modeled GPPs and satellite-derived NDVI. To date, satellite-based vegetation indices have often been used for the evaluation of terrestrial biosphere models in continental-scale analysis [33]. A possible method to conduct a quantitative comparison is to use GPPs of empirically upscaled products that rely on the dense network of eddy-covariance observations and satellite-based data [12]. The eddy-covariance network dataset in Asia is insufficient to cover various ecosystems in Asia, especially in Siberia and Southeast and South Asia [70]; further improvements in the dataset are required.
An improved solar radiation dataset is required to interpret the effects of solar radiation on the modeled GPP. In this study, we used empirically estimated surface radiation based on the MTCLIM model with corrections using satellite-based solar radiation data during the 2000–2010 period. The method relies on the assumption that variations in diurnal temperature changes are related to incoming solar radiation, which may produce large uncertainties in estimating solar radiation. Other satellite-based radiation data (e.g., SRB data; [76]) cover the period from 1983 to 2007; no data are available for the past 30 years. Solar radiation is one of the important variables that determines GPP [17]; improved solar radiation data are thus required to improve the analysis of GPP.

4. Conclusion

Many regions in Asia have experienced vegetation greening from 1982 to 2011. Trends in vegetation greening have been reproduced using multiple terrestrial biosphere models for most regions in Asia. The analysis in this study clearly showed statistically significant increases in the NDVI for almost 40% of the regions in Asia, whereas decreasing vegetation trends were found for only a small percentage of the studied regions (less than 5%). Among the nine sub-continental regions, seven regions showed statistically significant increases in the NDVI. Simulations using the terrestrial biosphere models showed vegetation greening trends that were consistent with the results for the NDVI in boreal and temperate regions.
Three terrestrial biosphere models were used to determine the causes of the detected increasing trend in the NDVI. The determined contributions of climate and atmospheric CO2 changes varied considerably among the models. Further assessment is required to determine the effect of CO2 fertilization on GPP and assess the sensitivity of the models to climate anomalies.

Acknowledgments

We acknowledge Takahiro Sasai for valuable comments and discussions. This research was supported by the Environment Research and Technology Development Fund (RFa-1201) of the Ministry of the Environment, Japan, JSPS KAKENHI Grant Number 25281003, and the Korea Meteorological Administration Research and Development Program under Grant CATER 2013-3030. RBM participation was made possible by funding from NASA Earth Science Division.

Conflict of Interest

The authors declare no conflict of interest.

References and Notes

  1. Piao, S.L.; Ito, A.; Li, S.G.; Huang, Y.; Ciais, P.; Wang, X.H.; Peng, S.S.; Nan, H.J.; Zhao, C.; Ahlström, A.; et al. The carbon budget of terrestrial ecosystems in East Asia over the last two decades. Biogeosciences 2012, 9, 3571–3586. [Google Scholar] [Green Version]
  2. Patra, P.K.; Canadell, J.G.; Houghton, R.A.; Piao, S.L.; Oh, N.H.; Ciais, P.; Manjunath, K.R.; Chhabra, A.; Wang, T.; Bhattacharya, T.; et al. The carbon budget of South Asia. Biogeosciences 2013, 10, 513–527. [Google Scholar]
  3. Dolman, A.J.; Shvidenko, A.; Schepaschenko, D.; Ciais, P.; Tchebakova, N.; Chen, T.; van der Molen, M.K.; Belelli Marchesini, L.; Maximov, T.C.; Maksyutov, S.; et al. An estimate of the terrestrial carbon budget of Russia using inventory-based, eddy covariance and inversion methods. Biogeosciences 2012, 9, 5323–5340. [Google Scholar] [Green Version]
  4. Chapin, F.S.; Sturm, M.; Serreze, M.C.; McFadden, J.P.; Key, J.R.; Lloyd, A.H.; McGuire, A.D.; Rupp, T.S.; Lynch, A.H.; Schimel, J.P.; et al. Role of land-surface changes in arctic summer warming. Science 2005, 310, 657–660. [Google Scholar]
  5. Le Quere, C.; Andres, R.J.; Boden, T.; Conway, T.; Houghton, R.A.; House, J.I.; Marland, G.; Peters, G.P.; van der Werf, G.R.; Ahlstrom, A.; et al. The global carbon budget 1959–2011. Earth Syst. Sci. Data 2013, 5, 165–183. [Google Scholar]
  6. Lepers, E.; Lambin, E.F.; Janetos, A.C.; DeFries, R.; Achard, F.; Ramankutty, N.; Scholes, R.J. A synthesis of information on rapid land-cover change for the period 1981–2000. Bioscience 2005, 55, 115–124. [Google Scholar]
  7. Liu, M.; Tian, H. China’s land cover and land use change from 1700 to 2005: Estimations from high-resolution satellite data and historical archives. Glob. Biogeochem. Cy. 2010, 24. [Google Scholar] [CrossRef]
  8. Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar]
  9. Zhou, L.M.; Tucker, C.J.; Kaufmann, R.K.; Slayback, D.; Shabanov, N.V.; Myneni, R.B. Variations in northern vegetation activity inferred from satellite data of vegetation index during 1981 to 1999. J. Geophys. Res 2001, 106, 20069–20083. [Google Scholar]
  10. Kawabata, A.; Ichii, K.; Yamaguchi, Y. Global monitoring of interannual changes in vegetation activities using NDVI and its relationships to temperature and precipitation. Int. J. Remote Sens 2001, 22, 1377–1382. [Google Scholar]
  11. Xiao, J.; Moody, A. Geographical distribution of global greening trends and their climatic correlates: 1982–1998. Int. J. Remote Sens 2005, 26, 2371–2390. [Google Scholar]
  12. Yang, F.; Ichii, K.; White, M.; Hashimoto, H.; Michaelis, A.; Votava, P.; Zhu, A.; Huete, A.; Running, S.; Nemani, R. Developing a continental-scale measure of gross primary production by combining MODIS and Ameriflux data through support vector machine approach. Remote Sens. Environ 2007, 110, 109–122. [Google Scholar]
  13. Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rodenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar]
  14. Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.; et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. 2011. [Google Scholar] [CrossRef]
  15. Xiao, J.; Zhuang, Q.; Law, B.E.; Chen, J.; Baldocchi, D.D.; Cook, D.R.; Oren, R.; Richardson, A.D.; Wharton, S.; Ma, S. A continuous measure of gross primary production for the conterminous United States derived from MODIS and Ameriflux data. Remote Sens. Environ 2010, 114, 576–591. [Google Scholar]
  16. Goetz, S.J.; Prince, S.D.; Goward, S.N.; Thawley, M.M.; Small, J. Satellite remote sensing of primary production: An improved production efficiency modeling approach. Ecol. Model 1999, 122, 239–255. [Google Scholar]
  17. Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar]
  18. Sasai, T.; Ichii, K.; Yamaguchi, Y.; Nemani, R. Simulating terrestrial carbon fluxes using the new biosphere model “Biosphere model integrating eco-physiological and mechanistic approaches using satellite data” (BEAMS). J. Geophys. Res. 2005. [Google Scholar] [CrossRef]
  19. Ito, A.; Oikawa, T. A simulation model of the carbon cycle in land ecosystems (Sim-cycle): A description based on dry-matter production theory and plot-scale validation. Ecol. Model 2002, 151, 143–176. [Google Scholar]
  20. Sitch, S.; Smith, B.; Prentice, I.C.; Arneth, A.; Bondeau, A.; Cramer, W.; Kaplan, J.O.; Levis, S.; Lucht, W.; Sykes, M.T.; et al. Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model. Glob. Chang. Biol 2003, 9, 161–185. [Google Scholar]
  21. Piao, S.; Wang, X.; Ciais, P.; Zhu, B.; Wang, T.A.O.; Liu, J.I.E. Changes in satellite-derived vegetation growth trend in temperate and boreal Eurasia from 1982 to 2006. Glob. Chang. Biol 2011, 17, 3228–3239. [Google Scholar]
  22. Piao, S. Interannual variations of monthly and seasonal normalized difference vegetation index (NDVI) in China from 1982 to 1999. J. Geophys. Res. 2003. [Google Scholar] [CrossRef]
  23. Peng, S.; Chen, A.; Xu, L.; Cao, C.; Fang, J.; Myneni, R.B.; Pinzon, J.E.; Tucker, C.J.; Piao, S. Recent change of vegetation growth trend in China. Environ. Res. Lett 2011, 6, 044027. [Google Scholar]
  24. Xiao, J.; Moody, A. Trends in vegetation activity and their climatic correlates: China 1982 to 1998. Int. J. Remote Sens 2004, 25, 5669–5689. [Google Scholar]
  25. Park, H.S.; Sohn, B.J. Recent trends in changes of vegetation over East Asia coupled with temperature and rainfall variations. J. Geophys. Res. 2010. [Google Scholar] [CrossRef]
  26. Jeong, S.-J.; Ho, C.-H.; Jeong, J.-H. Increase in vegetation greenness and decrease in springtime warming over East Asia. Geophys. Res. Lett. 2009. [Google Scholar] [CrossRef]
  27. Nagai, S.; Ichii, K.; Morimoto, H. Interannual variations in vegetation activities and climate variability caused by ENSO in tropical rainforests. Int. J. Remote Sens 2007, 28, 1285–1297. [Google Scholar]
  28. Bala, G.; Joshi, J.; Chaturvedi, R.; Gangamani, H.; Hashimoto, H.; Nemani, R. Trends and variability of AVHRR-derived NPP in India. Remote Sens 2013, 5, 810–829. [Google Scholar]
  29. Milesi, C.; Samanta, A.; Hashimoto, H.; Kumar, K.K.; Ganguly, S.; Thenkabail, P.S.; Srivastava, A.N.; Nemani, R.R.; Myneni, R.B. Decadal variations in NDVI and food production in India. Remote Sens 2010, 2, 758–776. [Google Scholar]
  30. Saigusa, N.; Ichii, K.; Murakami, H.; Hirata, R.; Asanuma, J.; Den, H.; Han, S.-J.; Ide, R.; Li, S.-G.; Ohta, T.; et al. Impact of meteorological anomalies in the 2003 summer on gross primary productivity in East Asia. Biogeosciences 2010, 7, 641–655. [Google Scholar]
  31. Piao, S.; Fang, J.; Zhou, L.; Zhu, B.; Tan, K.; Tao, S. Changes in vegetation net primary productivity from 1982 to 1999 in China. Glob. Biogeochem. Cy. 2005. [Google Scholar] [CrossRef]
  32. Lucht, W.; Prentice, I.C.; Myneni, R.B.; Sitch, S.; Friedlingstein, P.; Cramer, W.; Bousquet, P.; Buermann, W.; Smith, B. Climatic control of the high-latitude vegetation greening trend and Pinatubo effect. Science 2002, 296, 1687–1689. [Google Scholar]
  33. Hashimoto, H.; Melton, F.; Ichii, K.; Milesi, C.; Wang, W.; Nemani, R.R. Evaluating the impacts of climate and elevated carbon dioxide on tropical rainforests of the western Amazon basin using ecosystem models and satellite data. Glob. Chang. Biol 2010, 16, 255–271. [Google Scholar]
  34. Piao, S.; Friedlingstein, P.; Ciais, P.; Zhou, L.; Chen, A. Effect of climate and CO2 changes on the greening of the northern hemisphere over the past two decades. In Geophys. Res. Lett.; 2006. [Google Scholar] [CrossRef]
  35. Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ 2010, 114, 168–182. [Google Scholar]
  36. Takagi, H.; Saeki, T.; Oda, T.; Saito, M.; Valsala, V.; Belikov, D.; Saito, R.; Yoshida, Y.; Morino, I.; Uchino, O.; et al. On the benefit of GOSAT observations to the estimation of regional CO2 fluxes. Sola 2011, 7, 161–164. [Google Scholar]
  37. Tucker, C.; Pinzon, J.; Brown, M.; Slayback, D.; Pak, E.; Mahoney, R.; Vermote, E.; El Saleous, N. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT VEGETATION NDVI data. Int. J. Remote Sens 2005, 26, 4485–4498. [Google Scholar]
  38. Pinzon, J.E. Revisiting error, precision and uncertainty in NDVI AVHRR data: Development of a consistent NDVI3g time series. Remote Sens. in preparation..
  39. Veroustraete, F.; Patyn, J.; Myneni, R.B. Estimating net ecosystem exchange of carbon using the normalized difference vegetation index and an ecosystem model. Remote Sens. Environ 1996, 58, 115–130. [Google Scholar]
  40. Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.; Myneni, R. Global data sets of vegetation leaf area index (LAI)3g and fraction of photosynthetically active radiation (FPAR)3g derived from global inventory modeling and mapping studies (GIMMS) normalized difference vegetation index (NDVI3g) for the period 1981 to 2011. Remote Sens 2013, 5, 927–948. [Google Scholar]
  41. Sasai, T.; Okamoto, K.; Hiyama, T.; Yamaguchi, Y. Comparing terrestrial carbon fluxes from the scale of a flux tower to the global scale. Ecol. Model 2007, 208, 135–144. [Google Scholar]
  42. Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ 2002, 83, 214–231. [Google Scholar]
  43. Yuan, H.; Dai, Y.; Xiao, Z.; Ji, D.; Shangguan, W. Reprocessing the MODIS leaf area index products for land surface and climate modelling. Remote Sens. Environ 2011, 115, 1171–1187. [Google Scholar]
  44. CRUNCEP Data Set. Available online: http://nacp.ornl.gov/thredds/fileServer/reccapDriver/cru_ncep/analysis/readme.htm (accessed on 13 November 2013).
  45. Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations - the CRUTS3.10 dataset. Int. J. Climatol. 2013. [Google Scholar] [CrossRef]
  46. Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc 1996, 77, 437–471. [Google Scholar]
  47. Thornton, P.E.; Running, S.W. An improved algorithm for estimating incident daily solar radiation from measurements of temperature, humidity, and precipitation. Agric. For. Meteorol 1999, 93, 211–228. [Google Scholar]
  48. Frouin, R.; Murakami, H. Estimating photosynthetically available radiation at the ocean surface from ADEOS-II Global Imager data. J. Oceanogr 2007, 63, 493–503. [Google Scholar]
  49. Trends in Atmospheric Carbon Dioxide. Available online: http://www.esrl.noaa.gov/gmd/ccgg/trends/ (accessed on 13 October 2013).
  50. Historical CO2 Records from the Law Dome DE08, DE08–2, and DSS Ice Cores. Available online: http://cdiac.ornl.gov/trends/co2/lawdome.html (accessed on 13 October 2013).
  51. Global 30 Arc-Second Elevation (GTOPO30). Available online: https://lta.cr.usgs.gov/GTOPO30 (accessed on 13 October 2013).
  52. Schenk, H.J.; Jackson, R.B. ISLSCL II Ecosystem Rooting Depths; Oak Ridge National Laboratory Distributed Active Archive Center: Oak Ridge, TN, USA, 2009. [Google Scholar]
  53. Thornton, P.E.; Law, B.E.; Gholz, H.L.; Clark, K.L.; Falge, E.; Ellsworth, D.S.; Goldstein, A.H.; Monson, R.K.; Hollinger, D.; Falk, M.; et al. Modeling and measuring the effects of disturbance history and climate on carbon and water budgets in evergreen needleleaf forests. Agric. For. Meteorol 2002, 113, 185–222. [Google Scholar]
  54. Gerten, D.; Schaphoff, S.; Haberlandt, U.; Lucht, W.; Sitch, S. Terrestrial vegetation and water balance—hydrological evaluation of a dynamic global vegetation model. J. Hydrol 2004, 286, 249–270. [Google Scholar]
  55. Cox, P. Description of the “TRIFFID” Dynamic Global Vegetation Model; Hadley Center: Exeter, UK, 2001. [Google Scholar]
  56. Suzuki, T.; Ichii, K. Evaluation of a terrestrial carbon cycle submodel in an earth system model using networks of eddy covariance observations. Tellus B 2010, 62, 729–742. [Google Scholar]
  57. Farquhar, G.D.; Caemmerer, V.; Berry, J.A. A biochemical model of phytosynthetic CO2 assimilation in leaves of C3 species. Planta 1980, 149, 78–90. [Google Scholar]
  58. Collatz, G.; Ball, J.T.; Grivet, C.; Berry, J.A. Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: A model that includes a laminar boundary layer. Agric. For. Meteorol 1991, 54, 107–136. [Google Scholar]
  59. Ball, J.T.; Woodrow, I.E.; Berry, J.A. A Model Predicting Stomatal Conductance and Its Contribution to the Control of Photosynthesis under Different Environmental Conditions. In Progress in Photosynthesis Research; Biggins, J., Ed.; Marinus Nijhoff: Leiden, The Netherlands, 1987; Volume 4, pp. 221–224. [Google Scholar]
  60. Leuning, R. Modelling stomatal behavior and photosynthesis of eucalyptus grandis. Aust. J. Plant Physiol 1990, 17, 159–175. [Google Scholar]
  61. Jarvis, P.G. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. Trans. R. Soc. B-Biol. Sci 1976, 273, 593–610. [Google Scholar]
  62. Haxeltine, A.; Prentice, I.C. BIOME3: An equilibrium terrestrial biosphere model based on ecophysiological constraints, resource availability, and competition among plant functional types. Glob. Biogeochem. Cy 1996, 10, 693–709. [Google Scholar]
  63. Collatz, G.; Ribas-Carbo, M.; Berry, J. Coupled photosynthesis-stomatal conductance model for leaves of C4 plants. Aust. J. Plant Physiol 1992, 19, 519–538. [Google Scholar]
  64. Cox, P.M.; Betts, R.A.; Bunton, C.B.; Essery, R.L.H.; Rowntree, P.R.; Smith, J. The impact of new land surface physics on the GCM simulation of climate and climate sensitivity. Clim. Dyn 1999, 15, 183–203. [Google Scholar]
  65. Ichii, K.; Hashimoto, H.; Nemani, R.; White, M. Modeling the interannual variability and trends in gross and net primary productivity of tropical forests from 1982 to 1999. Glob. Planet. Chang 2005, 48, 274–286. [Google Scholar]
  66. Kendall, M.G. A new measure of rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar]
  67. Sokal, R.R.; Rohlf, F.J. Biometry: The Principles and Practice of Statistics in Biological Research, 3rd ed; W.H. Freeman: New York, NY, USA, 1995; p. 539. [Google Scholar]
  68. Kobayashi, H.; Dye, D.G. Atmospheric conditions for monitoring the long-term vegetation dynamics in the Amazon using normalized difference vegetation index. Remote Sens. Environ 2005, 97, 519–525. [Google Scholar]
  69. Ichii, K.; Kondo, M.; Lee, Y.-H.; Wang, S.-Q.; Kim, J.; Ueyama, M.; Lim, H.-J.; Shi, H.; Suzuki, T.; Ito, A.; et al. Site-level model—Data synthesis of terrestrial carbon fluxes in the CarboEastAsia eddy-covariance observation network: Toward future modeling efforts. J. For. Res 2013, 18, 13–20. [Google Scholar]
  70. Ichii, K.; Hashimoto, H.; White, M.A.; Potters, C.; Hutyra, L.R.; Huete, A.R.; Myneni, R.B.; Nemanis, R.R. Constraining rooting depths in tropical rainforests using satellite data and ecosystem modeling for accurate simulation of gross primary production seasonality. Glob. Chang. Biol 2007, 13, 67–77. [Google Scholar]
  71. Piao, S.; Sitch, S.; Ciais, P.; Friedlingstein, P.; Peylin, P.; Wang, X.; Ahlstrom, A.; Anav, A.; Canadell, J.G.; Cong, N.; et al. Evaluation of terrestrial carbon cycle models for their response to climate variability and to CO2 trends. Glob. Chang. Biol 2013, 19, 2117–2132. [Google Scholar]
  72. Ichii, K.; Suzuki, T.; Kato, T.; Ito, A.; Hajima, T.; Ueyama, M.; Sasai, T.; Hirata, R.; Saigusa, N.; Ohtani, Y.; et al. Multi-model analysis of terrestrial carbon cycles in Japan: Limitations and implications of model calibration using eddy flux observations. Biogeosciences 2010, 7, 2061–2080. [Google Scholar]
  73. Schwalm, C.R.; Williams, C.A.; Schaefer, K.; Anderson, R.; Arain, M.A.; Baker, I.; Barr, A.; Black, T.A.; Chen, G.; Chen, J.M.; et al. A model-data intercomparison of CO2 exchange across North America: Results from the North American Carbon Program site synthesis. J. Geophys. Res. 2010. [Google Scholar] [CrossRef]
  74. Jung, M.; le Maire, G.; Zaehle, S.; Luyssaert, S.; Vetter, M.; Churkina, G.; Ciais, P.; Viovy, N.; Reichstein, M. Assessing the ability of three land ecosystem models to simulate gross carbon uptake of forests from boreal to mediterranean climate in Europe. Biogeosciences 2007, 4, 647–656. [Google Scholar]
  75. Saigusa, N.; Li, S.-G.; Kwon, H.; Takagi, K.; Zhang, L.-M.; Ide, R.; Ueyama, M.; Asanuma, J.; Choi, Y.-J.; Chun, J.H.; et al. Dataset of CarboEastAsia and uncertainties in the CO2 budget evaluation caused by different data processing. J. For. Res 2013, 18, 41–48. [Google Scholar]
  76. SRB Data and Information. Available online: https://eosweb.larc..nasa.gov/project/srb/srb_table (accessed on 13 October 2013).
Remotesensing 05 06043f1 1024
Figure 1. (a) Land cover in the study regions. MODIS land-cover data (MCD12Q1) [35] were used. (b) The sub-continental division used in this study was based on the Greenhouse gases Observing Satellite (GOSAT) Level 4A product [36]. Abbreviations of the ecosystem types are evergreen needleleaf forest (ENF), evergreen broadleaf forest (EBF), deciduous needleleaf forest (DNF), deciduous broadleaf forest (DBF), and mixed forest (MF).
Figure 1. (a) Land cover in the study regions. MODIS land-cover data (MCD12Q1) [35] were used. (b) The sub-continental division used in this study was based on the Greenhouse gases Observing Satellite (GOSAT) Level 4A product [36]. Abbreviations of the ecosystem types are evergreen needleleaf forest (ENF), evergreen broadleaf forest (EBF), deciduous needleleaf forest (DNF), deciduous broadleaf forest (DBF), and mixed forest (MF).
Remotesensing 05 06043f1
Remotesensing 05 06043f2 1024
Figure 2. Trend in (a) growing season average temperature (°C·30 y−1) and (b) annual total precipitation (%·30 y−1) from 1982 to 2011. The trend slope was estimated using the Kendall robust line-fit method. Solid black lines in the map show the sub-continental division (only for the Eurasian continent) defined in Figure 1b.
Figure 2. Trend in (a) growing season average temperature (°C·30 y−1) and (b) annual total precipitation (%·30 y−1) from 1982 to 2011. The trend slope was estimated using the Kendall robust line-fit method. Solid black lines in the map show the sub-continental division (only for the Eurasian continent) defined in Figure 1b.
Remotesensing 05 06043f2
Remotesensing 05 06043f3 1024
Figure 3. Trend in growing season average Normalized Difference Vegetation Index (NDVI) from 1982 to 2011. Only grids with statistically significant trends (p < 0.05) are colored. The Mann-Kendall trend test was applied for the significance test; the slope was estimated using the Kendall robust line-fit method. Solid black lines in the map show the subcontinental division (only for the Eurasian continent) defined in Figure 1b.
Figure 3. Trend in growing season average Normalized Difference Vegetation Index (NDVI) from 1982 to 2011. Only grids with statistically significant trends (p < 0.05) are colored. The Mann-Kendall trend test was applied for the significance test; the slope was estimated using the Kendall robust line-fit method. Solid black lines in the map show the subcontinental division (only for the Eurasian continent) defined in Figure 1b.
Remotesensing 05 06043f3
Remotesensing 05 06043f4 1024
Figure 4. Interannual variations in the NDVI and annual GPP in each subcontinental region (Figure 1b and Table 1). Normalized NDVI anomalies and modeled GPPs (based on the average for the 1982–2011 period) are shown.
Figure 4. Interannual variations in the NDVI and annual GPP in each subcontinental region (Figure 1b and Table 1). Normalized NDVI anomalies and modeled GPPs (based on the average for the 1982–2011 period) are shown.
Remotesensing 05 06043f4
Remotesensing 05 06043f5 1024
Figure 5. Contribution of the modeled GPP trend of each individual factor (i.e., temperature, precipitation, solar radiation, and atmospheric CO2 concentration) as stacked bar graphs in each region ((a) Boreal Eurasia North West, (b) Boreal Eurasia North East, (c) Boreal Eurasia South West, (d) Boreal Eurasia South East, (e) Temperate Asia North West, (f) Temperate Asia North East, (g) Temperate Asia South East, (h) Tropical Asia North, and (i) Tropical Asia South). Cumulative sums of GPP trends for the simulations with each input data temporally changing are approximately consistent with the GPP trends in the simulation with all input data temporally changing (y = 1.21 x + 0.09, R2 = 0.92; x is the sum of GPP trends for the simulations with each input data changing in each region and for every model, and y represents the GPP trends for the simulation with all input data changing in each region and for each model; 27 data points (3 models × 9 sub-regions)).
Figure 5. Contribution of the modeled GPP trend of each individual factor (i.e., temperature, precipitation, solar radiation, and atmospheric CO2 concentration) as stacked bar graphs in each region ((a) Boreal Eurasia North West, (b) Boreal Eurasia North East, (c) Boreal Eurasia South West, (d) Boreal Eurasia South East, (e) Temperate Asia North West, (f) Temperate Asia North East, (g) Temperate Asia South East, (h) Tropical Asia North, and (i) Tropical Asia South). Cumulative sums of GPP trends for the simulations with each input data temporally changing are approximately consistent with the GPP trends in the simulation with all input data temporally changing (y = 1.21 x + 0.09, R2 = 0.92; x is the sum of GPP trends for the simulations with each input data changing in each region and for every model, and y represents the GPP trends for the simulation with all input data changing in each region and for each model; 27 data points (3 models × 9 sub-regions)).
Remotesensing 05 06043f5
Table
Table 1. Temporal trends in the NDVI (NDVI·30 y−1) and model-based gross primary productivity (GPP) (gC·m−2·y−2) from 1982 to 2011. Values in parentheses are model-based GPP trends (TgC·y−1).
Table 1. Temporal trends in the NDVI (NDVI·30 y−1) and model-based gross primary productivity (GPP) (gC·m−2·y−2) from 1982 to 2011. Values in parentheses are model-based GPP trends (TgC·y−1).
RegionNDVIBEAMSBiome-BGCLPJTRIFFID
Boreal Eurasia North West0.0150.5 (2.5)2.4 (9.2) **3.2 (11.8) **3.8** (14.6)
Boreal Eurasia North East0.068**1.3 (5.3) **3.6 (14.7) **5.0 (19.6) **5.7** (21.1)
Boreal Eurasia South West0.041**1.9 (5.5) **5.9 (16.5) **5.5 (15.3) **3.5** (9.2)
Boreal Eurasia South East0.034**1.8 (6.2) **1.9 (6.1) **3.4 (11.4) **0.8 (2.5)
Temperate Asia North West0.024**1.4 (4.6) **0.6 (2.3) *2.9 (9.3) *0.9** (3.0)
Temperate Asia North East0.020**1.7 (11.8) **2.5 (17.8) **1.3 (9.9) *1.4* (11.2)
Temperate Asia South East0.032**3.7 (15.5) **0.9 (4.1) **4.2 (17.4) **2.7** (11.6)
Tropical Asia North0.023*5.1 (21.2) **6.6 (27.2) **7.1 (29.9) **4.5** (18.9)
Tropical Asia South0.0133.0 (11.9) **11.8 (46.0) **7.9 (30.8) **7.9** (30.9)
Statistically significant trends are marked as
**(p < 0.05) and
*(p < 0.1).
Table
Table 2. Correlation coefficients between the NDVI and GPP from each terrestrial biosphere model. Correlation coefficients were calculated based on Kendall’s rank correlation coefficients (Kendall’s τ).
Table 2. Correlation coefficients between the NDVI and GPP from each terrestrial biosphere model. Correlation coefficients were calculated based on Kendall’s rank correlation coefficients (Kendall’s τ).
RegionBEAMSBiome-BGCLPJTRIFFID
Boreal Eurasia North West0.67**0.31*0.50**0.33*
Boreal Eurasia North East0.72**0.70**0.66**0.68**
Boreal Eurasia South West0.80**0.40**0.37**0.16
Boreal Eurasia South East0.71**0.45**0.46**0.37**
Temperate Asia North West0.83**0.49**0.51**0.57**
Temperate Asia North East0.76**0.44**0.44**0.39**
Temperate Asia South East0.74**0.54**0.55**0.48**
Tropical Asia North0.58**0.27*0.230.20
Tropical Asia South0.170.26*0.160.17
Statistically significant correlations are marked as
**(p < 0.01), and
*(p < 0.05).

Share and Cite

MDPI and ACS Style

Ichii, K.; Kondo, M.; Okabe, Y.; Ueyama, M.; Kobayashi, H.; Lee, S.-J.; Saigusa, N.; Zhu, Z.; Myneni, R.B. Recent Changes in Terrestrial Gross Primary Productivity in Asia from 1982 to 2011. Remote Sens. 2013, 5, 6043-6062. https://doi.org/10.3390/rs5116043

AMA Style

Ichii K, Kondo M, Okabe Y, Ueyama M, Kobayashi H, Lee S-J, Saigusa N, Zhu Z, Myneni RB. Recent Changes in Terrestrial Gross Primary Productivity in Asia from 1982 to 2011. Remote Sensing. 2013; 5(11):6043-6062. https://doi.org/10.3390/rs5116043

Chicago/Turabian Style

Ichii, Kazuhito, Masayuki Kondo, Yuki Okabe, Masahito Ueyama, Hideki Kobayashi, Seung-Jae Lee, Nobuko Saigusa, Zaichun Zhu, and Ranga B. Myneni. 2013. "Recent Changes in Terrestrial Gross Primary Productivity in Asia from 1982 to 2011" Remote Sensing 5, no. 11: 6043-6062. https://doi.org/10.3390/rs5116043

APA Style

Ichii, K., Kondo, M., Okabe, Y., Ueyama, M., Kobayashi, H., Lee, S. -J., Saigusa, N., Zhu, Z., & Myneni, R. B. (2013). Recent Changes in Terrestrial Gross Primary Productivity in Asia from 1982 to 2011. Remote Sensing, 5(11), 6043-6062. https://doi.org/10.3390/rs5116043

Article Metrics

Back to TopTop