Evaluating Parameter Adjustment in the MODIS Gross Primary Production Algorithm Based on Eddy Covariance Tower Measurements
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. Eddy-Covariance Data
2.1.2. MODIS 8-Day Average GPP Product
2.2. Model Description
2.2.1. MODIS GPP Algorithm
2.2.2. Farquhar Model
2.3. Model Simulation
2.3.1. Forcing Data
2.3.2. Parameter Selection and Optimization
2.3.3. Experiment
- LUE: A simulation with the MODIS GPP algorithm (Equaiton (1)) and optimized biome-parameters using EC measurements;
- LUE-SW: Addition of the soil water scale (Equation (5)) to the MODIS GPP algorithm. The parameters were optimized after the addition.
- LUEdef: A simulation with the MODIS GPP algorithm and the default biome-parameters supplied by BPLUT [20], which is aimed at testing default parameters forced by EC data;
- Farquhar: A simulation with the two-leaf Farquhar model (Equations (6) and (7)) to investigate structural error introduced by the one-leaf upscaling strategy and to validate compensation of parameter adjustment to the MODIS algorithm.
2.4. Model Performance
3. Results
3.1. Model Parameters Variation
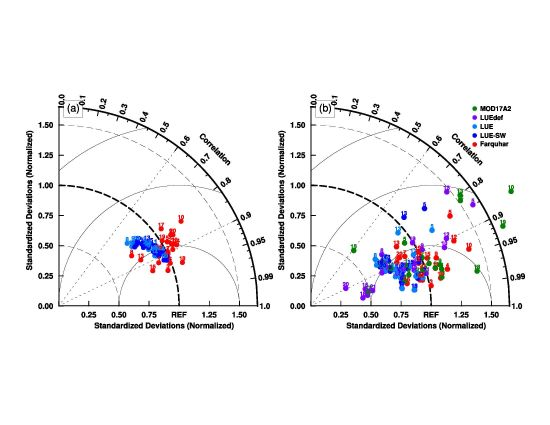
3.2. Model–Data Agreement on Half-Hourly and Daily Time Scales
3.3. Model–Data Agreement on Monthly and Seasonal Time Scales
4. Discussion
4.1. Uncertainties in Input Data and Parameters in MOD17A2
4.2. Uncertainties in Parameter Sets in the MODIS GPP Algorithm
4.3. Link between Parameter Sets and Model Structures
5. Conclusions
- (1)
- Large bias was observed in the MODIS GPP product, especially in deciduous forests and shrubs and grasslands. Its uncertainties were affected by both input data and the look-up table values of ɛmax for individual PFTs. It is necessary to optimize the parameters in the look-up table used by the MODIS algorithm, but the optimized parameters should correspond to specific input data for applications, i.e., the optimized parameters cannot be applied to a simulation with changed driver data because errors from parameters and input data can accumulate.
- (2)
- Optimizing the key parameter ɛmax in the MODIS GPP algorithm can compensate the errors caused by ignoring soil water factor at the site level, but the ɛmax values would have large uncertainties among sites within the same PFT and among the PFTs, especially for sites with low yearly average soil water factors. This result casts doubt on the accuracy of simulated spatial distribution of GPP yielded by the MODIS algorithm. Moreover, GPP was underestimated by the one-leaf models in summer, regardless of whether the soil water factor was considered, but could be improved by separating the canopy structure into sunlit and shaded parts. This result indicates that improving model structure is a better choice than only adjusting parameters. Photosynthetic dynamics in spring and fall for forests and shrubs and seasonal GPP change for grasslands could not be captured by both one-leaf and two-leaf models. Therefore, there is a need to improve seasonal and phenology variations of key parameters and variables in carbon assimilation calculation to reduce uncertainties in GPP simulation.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rodenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar]
- Bonan, G.B.; Lawrence, P.J.; Oleson, K.W.; Levis, S.; Jung, M.; Reichstein, M.; Lawrence, D.M.; Swenson, S.C. Improving canopy processes in the Community Land Model version 4 (CLM4) using global flux fields empirically inferred from fluxnet data. J. Geophys. Res 2011. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.; et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res 2011. [Google Scholar] [CrossRef]
- Chen, J.M.; Mo, G.; Pisek, J.; Liu, J.; Deng, F.; Ishizawa, M.; Chan, D. Effects of foliage clumping on the estimation of global terrestrial gross primary productivity. Glob. Biogeochem. Cy 2012. [Google Scholar] [CrossRef]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ 2005, 95, 164–176. [Google Scholar]
- Piao, S.; Sitch, S.; Ciais, P.; Friedlingstein, P.; Peylin, P.; Wang, X.; Ahlstrom, A.; Anav, A.; Canadell, J.G.; Cong, N.; et al. Evaluation of terrestrial carbon cycle models for their response to climate variability and to CO2 trends. Glob. Change Biol 2013, 19, 2117–2132. [Google Scholar]
- Chen, H.; Dickinson, R.E.; Dai, Y.; Zhou, L. Sensitivity of simulated terrestrial carbon assimilation and canopy transpiration to different stomatal conductance and carbon assimilation schemes. Clim. Dynam 2010, 36, 1037–1054. [Google Scholar]
- Kanniah, K.D.; Beringer, J.; Hutley, L.B.; Tapper, N.J.; Zhu, X. Evaluation of collections 4 and 5 of the MODIS gross primary productivity product and algorithm improvement at a tropical savanna site in northern Australia. Remote Sens. Environ 2009, 113, 1808–1822. [Google Scholar]
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol 1972, 9, 747–766. [Google Scholar]
- Farquhar, G.D.; Caemmerer, S.V.; Berry, J.A. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 1980, 149, 78–90. [Google Scholar]
- Beer, C.; Reichstein, M.; Ciais, P.; Farquhar, G.D.; Papale, D. Mean annual GPP of Europe derived from its water balance. Geophys. Res. Lett 2007. [Google Scholar] [CrossRef]
- Thurner, M.; Beer, C.; Santoro, M.; Carvalhais, N.; Wutzler, T.; Schepaschenko, D.; Shvidenko, A.; Kompter, E.; Ahrens, B.; Levick, S.R.; et al. Carbon stock and density of northern boreal and temperate forests. Glob. Ecol. Biogeogr 2013. [Google Scholar] [CrossRef]
- He, M.; Zhou, Y.; Ju, W.; Chen, J.; Zhang, L.; Wang, S.; Saigusa, N.; Hirata, R.; Murayama, S.; Liu, Y. Evaluation and improvement of MODIS gross primary productivity in typical forest ecosystems of east Asia based on eddy covariance measurements. J. Forest Res 2013, 18, 31–40. [Google Scholar]
- Sjöström, M.; Zhao, M.; Archibald, S.; Arneth, A.; Cappelaere, B.; Falk, U.; de Grandcourt, A.; Hanan, N.; Kergoat, L.; Kutsch, W.; et al. Evaluation of MODIS gross primary productivity for Africa using eddy covariance data. Remote Sens. Environ 2013, 131, 275–286. [Google Scholar]
- He, M.; Ju, W.; Zhou, Y.; Chen, J.; He, H.; Wang, S.; Wang, H.; Guan, D.; Yan, J.; Li, Y.; et al. Development of a two-leaf light use efficiency model for improving the calculation of terrestrial gross primary productivity. Agric. Forest Meteorol 2013, 173, 28–39. [Google Scholar]
- Yuan, W.; Liu, S.; Zhou, G.; Zhou, G.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. Forest Meteorol 2007, 143, 189–207. [Google Scholar]
- Xiao, X.; Zhang, Q.; Hollinger, D.; Aber, J.; Moore, B. Modeling gross primary production of an evergreen needleleaf forest using MODIS and climate data. Ecol. Appl 2005, 15, 954–969. [Google Scholar]
- Wu, C.; Munger, J.W.; Niu, Z.; Kuang, D. Comparison of multiple models for estimating gross primary production using MODIS and eddy covariance data in harvard forest. Remote Sens. Environ 2010, 114, 2925–2939. [Google Scholar]
- Heinsch, F.A.; Reeves, M.; Votava, P.; Kang, S.; Milesi, C.; Zhao, M.; Glassy, J.; Jolly, W.M.; Loehman, R.; Bowker, C.F.; et al. User’s Guide GPP and NPP (MOD17A2/A3) Products NASA MODIS Land Algorithm; Version 2.0; MODIS Land Team: Washington, DC, USA, 2003; p. 17. [Google Scholar]
- Zhao, M.; Running, S.W. Drought-induced reduction in global terrestrial net primary production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Zhao, M.; Running, S.W.; Wofsy, S.C.; Urbanski, S.; Dunn, A.L.; Munger, J.W. Scaling gross primary production (GPP) over boreal and deciduous forest landscapes in support of MODIS GPP product validation. Remote Sens. Environ 2003, 88, 256–270. [Google Scholar]
- Sims, D.; Rahman, A.; Cordova, V.; Elmasri, B.; Baldocchi, D.; Bolstad, P.; Flanagan, L.; Goldstein, A.; Hollinger, D.; Misson, L. A new model of gross primary productivity for north American ecosystems based solely on the enhanced vegetation index and land surface temperature from MODIS. Remote Sens. Environ 2008, 112, 1633–1646. [Google Scholar]
- Wu, C.; Niu, Z.; Gao, S. Gross primary production estimation from MODIS data with vegetation index and photosynthetically active radiation in maize. J. Geophys. Res 2010. doi: 12110.11029/12009JD013023. [Google Scholar]
- Zhang, F.; Chen, J.M.; Chen, J.; Gough, C.M.; Martin, T.A.; Dragoni, D. Evaluating spatial and temporal patterns of MODIS GPP over the conterminous U.S. Against flux measurements and a process model. Remote Sens. Environ 2012, 124, 717–729. [Google Scholar]
- Dai, Y.; Dickinson, R.E.; Wang, Y.P. A two-big-leaf model for canopy temperature, photosynthesis and stomatal conductance. J. Clim 2004, 17, 2281–2299. [Google Scholar]
- Sprintsin, M.; Chen, J.M.; Desai, A.; Gough, C.M. Evaluation of leaf-to-canopy upscaling methodologies against carbon flux data in north america. J. Geophys. Res 2012. [Google Scholar] [CrossRef]
- Wang, X.; Ma, M.; Li, X.; Song, Y.; Tan, J.; Huang, G.; Zhang, Z.; Zhao, T.; Feng, J.; Ma, Z.; et al. Validation of MODIS-GPP product at 10 flux sites in northern China. Int. J. Remote Sens 2013, 34, 587–599. [Google Scholar]
- Hashimoto, H.; Wang, W.; Milesi, C.; Xiong, J.; Ganguly, S.; Zhu, Z.; Nemani, R. Structural uncertainty in model-simulated trends of global gross primary production. Remote Sens 2013, 5, 1258–1273. [Google Scholar]
- Mäkelä, A.; Pulkkinen, M.; Kolari, P.; Lagergren, F.; Berbigier, P.; Lindroth, A.; Loustau, D.; Nikinmaa, E.; Vesala, T.; Hari, P. Developing an empirical model of stand GPP with the LUE approach: Analysis of eddy covariance data at five contrasting conifer sites in Europe. Glob. Chang. Biol 2008, 14, 92–108. [Google Scholar]
- Mu, Q.; Zhao, M.; Heinsch, F.A.; Liu, M.; Tian, H.; Running, S.W. Evaluating water stress controls on primary production in biogeochemical and remote sensing based models. J. Geophys. Res 2007. [Google Scholar] [CrossRef]
- Keenan, T.F.; Davidson, E.; Moffat, A.M.; Munger, W.; Richardson, A.D. Using model-data fusion to interpret past trends, and quantify uncertainties in future projections, of terrestrial ecosystem carbon cycling. Glob. Chang. Biol 2012, 18, 2555–2569. [Google Scholar]
- Chen, B.; Chen, J.M.; Ju, W. Remote sensing-based ecosystem–atmosphere simulation scheme (EASS)—Model formulation and test with multiple-year data. Ecol. Model 2007, 209, 277–300. [Google Scholar]
- Chen, J.; Chen, B.; Black, T.A.; Innes, J.L.; Wang, G.; Kiely, G.; Hirano, T.; Wohlfahrt, G. Comparison of terrestrial evapotranspiration estimates using the mass-transfer and Penman-Monteith equations in land-surface models. J. Geophys. Res 2013. [Google Scholar] [CrossRef]
- Wilson, K.B.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at fluxnet sites. Agric. Forest Meteorol 2002, 113, 223–243. [Google Scholar]
- Stoy, P.C.; Mauder, M.; Foken, T.; Marcolla, B.; Boegh, E.; Ibrom, A.; Arain, M.A.; Arneth, A.; Aurela, M.; Bernhofer, C.; et al. A data-driven analysis of energy balance closure across fluxnet research sites: The role of landscape scale heterogeneity. Agric. Forest Meteorol 2013, (171–172), 137–152. [Google Scholar]
- Schaefer, K.; Schwalm, C.R.; Williams, C.; Arain, M.A.; Barr, A.; Chen, J.M.; Davis, K.J.; Dimitrov, D.; Hilton, T.W.; Hollinger, D.Y.; et al. A model-data comparison of gross primary productivity: Results from the north American carbon program site synthesis. J. Geophys. Res 2012. [Google Scholar] [CrossRef]
- Oleson, K.W.; Lawrence, D.M.; Bonan, G.B.; Flanner, M.G.; Kluzek, E.; Lawrence, P.J.; Levis, S.; Swenson, S.C.; Thornton, P.E.; Dai, A.; et al. Technical Description of Version 4.0 of the Community Land Model (CLM); National Center for Atmospheric Research: Boulder, CO, USA, 2010. [Google Scholar]
- Chen, B.; Coops, N.C.; Andy Black, T.; Jassal, R.S.; Chen, J.M.; Johnson, M. Modeling to discern nitrogen fertilization impacts on carbon sequestration in a pacific northwest douglas-fir forest in the first-postfertilization year. Glob. Chang. Biol 2011, 17, 1442–1460. [Google Scholar]
- Krishnan, P.; Black, T.A.; Jassal, R.S.; Chen, B.; Nesic, Z. Interannual variability of the carbon balance of three different-aged douglas-fir stands in the pacific northwest. J. Geophys. Res 2009. [Google Scholar] [CrossRef]
- Grant, R.F.; Barr, A.G.; Black, T.A.; Margolis, H.A.; McCaughey, J.H.; Trofymow, J.A. Net ecosystem productivity of temperate and boreal forests after clearcutting a fluxnet-Canada measurement and modelling synthesis. Tellus B 2010, 62, 475–496. [Google Scholar]
- Grünwald, T.; Bernhofer, C. A decade of carbon, water and energy flux measurements of an old spruce forest at the Anchor Station Tharandt. Tellus B 2007, 59, 387–396. [Google Scholar]
- Blyth, E.; Gash, J.; Lloyd, A.; Pryor, M.; Weedon, G.P.; Shuttleworth, J. Evaluating the JULES land surface model energy fluxes using fluxnet data. J. Hydrometeorol 2010, 11, 509–519. [Google Scholar]
- Hollinger, D.Y.; Aber, J.; Dail, B.; Davidson, E.A.; Goltz, S.M.; Hughes, H.; Leclerc, M.Y.; Lee, J.T.; Richardson, A.D.; Rodrigues, C.; et al. Spatial and temporal variability in forest-atmosphere CO2 exchange. Glob. Chang. Biol 2004, 10, 1689–1706. [Google Scholar]
- Li, X.; Liu, Q.; Cai, Z.; Ma, Z. Specificleaf area and leaf area index of conifer plantations in Qianyanzhou station of subtropical China. J. Plant Ecol 2007, 31, 93–101. (In Chinese) [Google Scholar]
- Bergeron, O.; Margolis, H.A.; Black, T.A.; Coursolle, C.; Dunn, A.L.; Barr, A.G.; Wofsy, S.C. Comparison of carbon dioxide fluxes over three boreal black spruce forests in Canada. Glob. Chang. Biol 2007, 13, 89–107. [Google Scholar]
- Kljun, N.; Black, T.A.; Griffis, T.J.; Barr, A.G.; Gaumont-Guay, D.; Morgenstern, K.; McCaughey, J.H.; Nesic, Z. Response of net ecosystem productivity of three boreal forest stands to drought. Ecosystems 2006, 9, 1128–1144. [Google Scholar]
- Gaumont-Guay, D.; Black, T.A.; Barr, A.G.; Griffis, T.J.; Jassal, R.S.; Krishnan, P.; Grant, N.; Nesic, Z. Eight years of forest-floor CO2 exchange in a boreal black spruce forest: spatial integration and long-term temporal trends. Agric. Forest Meteorol 2014, 184, 25–35. [Google Scholar]
- Hill, T.C.; Williams, M.; Woodward, F.I.; Moncrieff, J.B. Constraining ecosystem processes from tower fluxes and atmospheric profile. Ecol. Appl 2011, 21, 1474–1489. [Google Scholar]
- Tanja, S.; Berninger, F.; Sala, T.V.; Markkanen, T.I.; Hari, P.; MaKela, A.; Ilvesniemi, H.; Hanninen, H.; Nikinmaa, E.; Huttula, T.; et al. Air temperature triggers the recovery of evergreen boreal forest photosynthesis in spring. Glob. Chang. Biol 2003, 9, 1410–1426. [Google Scholar]
- Rambal, S.; Ourcival, J.E.-M.; Joffre, R.; Mouillot, F.L.; Nouvellon, Y.; Reichstein, M.; Rocheteauz, A. Drought controls over conductance and assimilation of a mediterranean evergreen ecosystem: scaling from leaf to canopy. Glob. Chang. Biol 2003, 9, 1813–1824. [Google Scholar]
- Garbulsky, M.F.; PeÑUelas, J.; Papale, D.; Filella, I. Remote estimation of carbon dioxide uptake by a mediterranean forest. Glob. Chang. Biol 2008, 14, 2860–2867. [Google Scholar]
- Reichstein, M.; Ciais, P.; Papale, D.; Valentini, R.; Running, S.; Viovy, N.; Cramer, W.; Granier, A.; Ogee, J.; Allard, V.; et al. Reduction of ecosystem productivity and respiration during the european summer 2003 climate anomaly: A joint flux tower, remote sensing and modelling analysis. Glob. Chang. Biol 2007, 13, 634–651. [Google Scholar]
- Valentini, R.; Angelis, P.D.; Matteuci, G.; Monaco, R.; Dore, S.; Mucnozza, G.E.S. Seasonal net carbon dioxide exchange of a beech forest with the atmosphere. Glob. Chang. Biol 1996, 2, 199–207. [Google Scholar]
- Gu, L.; Meyers, T.; Pallardy, S.G.; Hanson, P.J.; Yang, B.; Heuer, M.; Hosman, K.P.; Riggs, J.S.; Sluss, D.; Wullschleger, S.D. Direct and indirect effects of atmospheric conditions and soil moisture on surface energy partitioning revealed by a prolonged drought at a temperate forest site. J. Geophys. Res 2006. [Google Scholar] [CrossRef]
- Barr, A.G.; Black, T.A.; Hogg, E.H.; Griffis, T.J.; Morgenstern, K.; Kljun, N.; Theede, A.; Nesic, Z. Climatic controls on the carbon and water balances of a boreal aspen forest, 1994–2003. Glob. Chang. Biol 2007, 13, 561–576. [Google Scholar]
- Krishnan, P.; Black, T.A.; Grant, N.J.; Barr, A.G.; Hogg, E.H.; Jassal, R.S.; Morgenstern, K. Impact of changing soil moisture distribution on net ecosystem productivity of a boreal aspen forest during and following drought. Agric. Forest Meteorol 2006, 139, 208–223. [Google Scholar]
- Pilegaard, K.; Ambus, P.; Mikkelsen, T.N.; Beier, C.; Ro-Poulsen, H. Field measurements of atmosphere-biosphere interactions in a danish beech forest. Boreal Environ. Res 2003, 8, 315–333. [Google Scholar]
- Lafleur, P.M.; Roulet, N.T.; Bubier, J.L.; Frolking, S.; Moore, T.R. Interannual variability in the peatland-atmosphere carbon dioxide exchange at an ombrotrophic bog. Glob. Biogeochem. Cy 2003. [Google Scholar] [CrossRef]
- Roulet, N.T.; Lafleur, P.M.; Richard, P.J.H.; Moore, T.R.; Humphreys, E.R.; Bubier, J. Contemporary carbon balance and late holocene carbon accumulation in a northern peatland. Glob. Chang. Biol 2007, 13, 397–411. [Google Scholar]
- Goulden, M.L.; Winston, G.C.; McMillan, A.M.S.; Litvak, M.E.; Read, E.L.; Rocha, A.V.; Rob Elliot, J. An eddy covariance mesonet to measure the effect of forest age on land-atmosphere exchange. Glob. Chang. Biol 2006, 12, 2146–2162. [Google Scholar]
- McMillan, A.M.S.; Winston, G.C.; Goulden, M.L. Age-dependent response of boreal forest to temperature and rainfall variability. Glob. Chang. Biol 2008, 14, 1904–1916. [Google Scholar]
- Wohlfahrt, G.; Hammerle, A.; Haslwanter, A.; Bahn, M.; Tappeiner, U.; Cernusca, A. Seasonal and inter-annual variability of the net ecosystem CO2 exchange of a temperate mountain grassland: Effects of weather and management. J. Geophys. Res 2008. doi: 08110.01029/02007JD009286. [Google Scholar]
- Montaldo, N.; Albertson, J.D.; Mancini, M. Dynamic calibration with an ensemble Kalman filter based data assimilation approach for root-zone moisture predictions. J. Hydrometeorol 2007, 8, 910–921. [Google Scholar]
- Peichl, M.; Leahy, P.; Kiely, G. Six-year stable annual uptake of carbon dioxide in intensively managed humid temperate grassland. Ecosystems 2010, 14, 112–126. [Google Scholar]
- Zhao, M.; Running, S.W.; Nemani, R.R. Sensitivity of moderate resolution imaging spectroradiometer (MODIS) terrestrial primary production to the accuracy of meteorological reanalyses. J. Geophys. Res 2006. doi: 01010.01029/02004JG000004. [Google Scholar]
- Chen, B.; Coops, N.C.; Fu, D.; Margolis, H.A.; Amiro, B.D.; Barr, A.G.; Black, T.A.; Arain, M.A.; Bourque, C.P.A.; Flanagan, L.B.; et al. Assessing eddy-covariance flux tower location bias across the fluxnet-canada research network based on remote sensing and footprint modelling. Agric. Forest Meteorol 2011, 151, 87–100. [Google Scholar]
- Chasmer, L.; Barr, A.; Hopkinson, C.; McCaughey, H.; Treitz, P.; Black, A.; Shashkov, A. Scaling and assessment of GPP from MODIS using a combination of airborne lidar and eddy covariance measurements over jack pine forests. Remote Sens. Environ 2009, 113, 82–93. [Google Scholar]
- Xiao, J.; Zhuang, Q.; Law, B.E.; Chen, J.; Baldocchi, D.D.; Cook, D.R.; Oren, R.; Richardson, A.D.; Wharton, S.; Ma, S. A continuous measure of gross primary production for the conterminous united states derived from MODIS and Ameriflux data. Remote Sens. Environ 2010, 114, 576–591. [Google Scholar]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, Maosheng; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. BioScience 2004, 54, 547–560. [Google Scholar]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Running, S.W.; Zhao, M.; Costa, M.H.; Kirschbaum, A.A.; Ham, J.M.; Saleska, S.R.; et al. Evaluation of MODIS NPP and GPP products across multiple biomes. Remote Sens. Environ 2006, 102, 282–292. [Google Scholar]
- Propastin, P.; Ibrom, A.; Knohl, A.; Erasmi, S. Effects of canopy photosynthesis saturation on the estimation of gross primary productivity from MODIS data in a tropical forest. Remote Sens. Environ 2012, 121, 252–260. [Google Scholar]
- Hu, Z.; Li, S.; Yu, G.; Sun, X.; Zhang, L.; Han, S.; Li, Y. Modeling evapotranspiration by combing a two-source model, a leaf stomatal model, and a light-use efficiency model. J. Hydrol 2013, 501, 186–192. [Google Scholar]
- Chen, J.M.; Liu, J.; Cihlar, J.; Goulden, M.L. Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications. Ecol. Model 1999, 124, 99–119. [Google Scholar]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, R.; Clement, R.; Dolman, H.; et al. Gap filling strategies for defensible annual sums of net ecosystem exchange. Agric. Forest Meteorol 2001, 107, 43–69. [Google Scholar]
- Moffat, A.M.; Papale, D.; Reichstein, M.; Hollinger, D.Y.; Richardson, A.D.; Barr, A.G.; Beckstein, C.; Braswell, B.H.; Churkina, G.; Desai, A.R.; et al. Comprehensive comparison of gap-filling techniques for eddy covariance net carbon fluxes. Agric. Forest Meteorol 2007, 147, 209–232. [Google Scholar]
- Chen, J.M.; Menges, C.H.; Leblanc, S.G. Global mapping of foliage clumping index using multi-angular satellite data. Remote Sens. Environ 2005, 97, 447–457. [Google Scholar]
- Deng, F.; Chen, J.M.; Plummer, S.; Mingzhen, C.; Pisek, J. Algorithm for global leaf area index retrieval using satellite imagery. IEEE Tran. Geosci. Remote Sens 2006, 44, 2219–2229. [Google Scholar]
- Qian, T.; Dai, A.; Trenberth, K.E.; Oleson, K.W. Simulation of global land surface conditions from 1948 to 2004. Part I: Forcing data and evaluations. J. Hydrometeorol 2006, 7, 953–975. [Google Scholar]
- Lawrence, D.M.; Oleson, K.W.; Flanner, M.G.; Thornton, P.E.; Swenson, S.C.; Lawrence, P.J.; Zeng, X.; Yang, Z.L.; Levis, S.; Sakaguchi, K.; et al. Parameterization improvements and functional and structural advances in version 4 of the community land model. J. Adv. Model. Earth Syst 2011. doi: 03010.01029/02011MS000045. [Google Scholar]
- Mo, X.; Chen, J.M.; Ju, W.; Black, T.A. Optimization of ecosystem model parameters through assimilating eddy covariance flux data with an ensemble kalman filter. Ecol. Model 2008, 217, 157–173. [Google Scholar]
- Groenendijk, M.; Dolman, A.J.; van der Molen, M.K.; Leuning, R.; Arneth, A.; Delpierre, N.; Gash, J.H.C.; Lindroth, A.; Richardson, A.D.; Verbeeck, H.; et al. Assessing parameter variability in a photosynthesis model within and between plant functional types using global fluxnet eddy covariance data. Agric. Forest Meteorol 2011, 151, 22–38. [Google Scholar]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meterol. Soc 1982, 63, 1309–1313. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res 2005, 30, 79–82. [Google Scholar]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res 1985, 90, 8995–9005. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res 2001, 106, 7183–7192. [Google Scholar]
- Schwalm, C.R.; Williams, C.A.; Schaefer, K.; Anderson, R.; Arain, M.A.; Baker, I.; Barr, A.; Black, T.A.; Chen, G.; Chen, J.M.; et al. A model-data intercomparison of CO2 exchange across north America: Results from the north American carbon program site synthesis. J. Geophys. Res 2010. [Google Scholar] [CrossRef] [Green Version]
- John, R.; Chen, J.; Noormets, A.; Xiao, X.; Xu, J.; Lu, N.; Chen, S. Modelling gross primary production in semi-arid inner Mongolia using MODIS imagery and eddy covariance data. Int. J. Remote. Sens 2013, 34, 2829–2857. [Google Scholar]
- Coops, N.; Black, T.; Jassal, R.; Trofymow, J.; Morgenstern, K. Comparison of MODIS, eddy covariance determined and physiologically modelled gross primary production (GPP) in a douglas-fir forest stand. Remote Sens. Environ 2007, 107, 385–401. [Google Scholar]
- Schubert, P.; Lagergren, F.; Aurela, M.; Christensen, T.; Grelle, A.; Heliasz, M.; Klemedtsson, L.; Lindroth, A.; Pilegaard, K.; Vesala, T.; et al. Modeling GPP in the nordic forest landscape with MODIS time series data—Comparison with the MODIS GPP product. Remote Sens. Environ 2012, 126, 136–147. [Google Scholar]
- Heinsch, F.A.; Zhao, M.; Running, S.W.; Kimball, J.S.; Nemani, R.R.; Davis, K.J.; Bolstad, P.V.; Cook, B.D.; Desai, A.R.; Ricciuto, D.M.; et al. Evaluation of remote sensing based terrestrial productivity from MODIS using regional tower eddy flux network observations. IEEE Tran. Geosci. Remote Sens 2006, 44, 1908–1923. [Google Scholar]
- Cracknell, A.P.; Kanniah, K.D.; Tan, K.P.; Wang, L. Evaluation of MODIS gross primary productivity and land cover products for the humid tropics using oil palm trees in Peninsular Malaysia and Google Earth imagery. Int. J. Remote Sens 2013, 34, 7400–7423. [Google Scholar]
- Garbulsky, M.F.; Peñuelas, J.; Papale, D.; Ardö, J.; Goulden, M.L.; Kiely, G.; Richardson, A.D.; Rotenberg, E.; Veenendaal, E.M.; Filella, I. Patterns and controls of the variability of radiation use efficiency and primary productivity across terrestrial ecosystems. Glob. Ecol. Biogeogr 2010, 19, 253–267. [Google Scholar]
- Yang, F.; Ichii, K.; White, M.A.; Hashimoto, H.; Michaelis, A.R.; Votava, P.; Zhu, A.X.; Huete, A.; Running, S.W.; Nemani, R.R. Developing a continental-scale measure of gross primary production by combining MODIS and Ameriflux data through support vector machine approach. Remote Sens. Environ 2007, 110, 109–122. [Google Scholar]
- Chen, J.M.; Black, T.A. Measuring leaf-area index of plant canopies with branch architecture. Agric. Forest Meteorol 1991, 57, 1–12. [Google Scholar]
- Macfarlane, C.; Hoffman, M.; Eamus, D.; Kerp, N.; Higginson, S.; McMurtrie, R.; Adams, M. Estimation of leaf area index in eucalypt forest using digital photography. Agric. Forest Meteorol 2007, 143, 176–188. [Google Scholar]
- Nightingale, J.M.; Coops, N.C.; Waring, R.H.; Hargrove, W.W. Comparison of MODIS gross primary production estimates for forests across the U.S.A. With those generated by a simple process model, 3-PGS. Remote Sens. Environ 2007, 109, 500–509. [Google Scholar]
- Pury, D.G.G.D.; Farquhar, G.D. Simple scaling of photosynthesis from leaves to canopies without the errors of big-leaf model. Plant Cell Environ 1997, 20, 537–557. [Google Scholar]
- Wang, Y.P.; Leuning, R. A two-leaf model for canopy conductance, photosynthesis and partitioning of available energy I: Model description and comparison with a multi-layered model. Agric. Forest Meteorol 1998, 91, 89–111. [Google Scholar]
- Muraoka, H.; Saigusa, N.; Nasahara, K.N.; Noda, H.; Yoshino, J.; Saitoh, T.M.; Nagai, S.; Murayama, S.; Koizumi, H. Effects of seasonal and interannual variations in leaf photosynthesis and canopy leaf area index on gross primary production of a cool-temperate deciduous broadleaf forest in Takayama, Japan. J. Plant Res 2010, 123, 563–576. [Google Scholar]
- Groenendijk, M.; Dolman, A.J.; Ammann, C.; Arneth, A.; Cescatti, A.; Dragoni, D.; Gash, J.H.C.; Gianelle, D.; Gioli, B.; Kiely, G.; et al. Seasonal variation of photosynthetic model parameters and leaf area index from global fluxnet eddy covariance data. J. Geophys. Res 2011. [Google Scholar] [CrossRef]
- Zhu, G.F.; Li, X.; Su, Y.H.; Lu, L.; Huang, C.L. Seasonal fluctuations and temperature dependence in photosynthetic parameters and stomatal conductance at the leaf scale of populus euphratica Oliv. Tree Physiol 2011, 31, 178–195. [Google Scholar]
- Ichii, K.; Hashimoto, H.; White, M.A.; Potter, C.; Hutyra, L.R.; Huete, A.R.; Myneni, R.B.; Nemani, R.R. Constraining rooting depths in tropical rainforests using satellite data and ecosystem modeling for accurate simulation of gross primary production seasonality. Glob. Chang. Biol 2007, 13, 67–77. [Google Scholar]
Appendix
Photosynthesis in the Dynamic Land Model
References
- Ball, J.T.; Woodrow, I.E.; Berry, J.A. A Model Predicting Stomatal Conductance and Its Contribution to th Control of Photosynthesis under Different Envrionmental Conditions. In Progress in Photosynthesis Research; Biggins, J., Ed.; Martinus Nijhoff: Dordrecht, The Nertherlands, 1987; pp. 221–224. [Google Scholar]
- Tang, S.; Chen, J.M.; Zhu, Q.; Li, X.; Chen, M.; Sun, R.; Zhou, Y.; Deng, F.; Xie, D. LAI inversion algorithm based on directional reflectance kernels. J. Environ. Manag 2007, 85, 638–648. [Google Scholar]





| Number | Site ID a | Latitude (°N) | Longitude (°E) | Elevation (m) | Biome Type b | Climate Zone | Site-Years | Precipitation (mm·yr−1) | LAImax (m2·m−2) | References |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | CA-Ca1 | 49.867 | −125.334 | 313 | NEF | Temperate | 2001–08(06) c | 1456 | 7.3 | Chen et al. (2011), Krishnan et al. (2009) [38,39] |
| 2 | CA-Ca2 | 49.871 | −125.291 | 170 | NEF | Temperate | 2007–10(08) | 619 | 2.7 | Grant et al. (2010) [40] |
| 3 | CA-Ca3 | 49.535 | −124.900 | 153 | NEF | Temperate | 2003–07(05) | 1683 | 7.0 | Grant et al. (2010) [40] |
| 4 | DE-Tha | 50.964 | 13.567 | 380 | NEF | Temperate | 2001–05(01) | 804 | 7.6 | Grünwald and Bernhofer (2007) [41] |
| 5 | ES-ES1 | 39.346 | −0.319 | 1 | NEF | Mediterranean | 2004–07(05) | 414 | 2.6 | Blyth et al. (2010) [42] |
| 6 | US-Ho1 | 45.204 | −68.740 | 72 | NEF | Temperate | 1996–98, 2003–04(03) | 951 | 5.7 | Hollinger et al. (2004) [43] |
| 7 | CN-Qia | 26.741 | 115.058 | 86 | NEF | Temperate | 2003–04, 2006–07(04) | 1325 | 4.7 | Li et al. (2007) [44] |
| 8 | CA-Ojp | 53.916 | −104.692 | 518 | NEF | Boreal | 2007–10(08) | 418 | 2.0 | Bergeron et al. (2007), Kljun et al. (2006) [45,46] |
| 9 | CA-Obs | 53.987 | −105.118 | 598 | NEF | Boreal | 2001–05(01) | 408 | 3.4 | Gaumont-Guay et al. (2014) [47] |
| 10 | CA-NS1 | 55.879 | −98.484 | 253 | NDF | Boreal | 2002–06(03) | 213 | 3.0c | Hill et al. (2011) [48] |
| 11 | FI-Hyy | 61.847 | 24.295 | 185 | NDF | Boreal | 2005–08(06) | 500 | 6.7 | Tanja et al. (2003) [49] |
| 12 | FR-Pue | 43.741 | 3.596 | 270 | BEF | Mediterranean | 2004–09(08) | 1116 | 2.9 | Rambal et al. (2003) [50] |
| 13 | IT-Cpz | 41.705 | 12.376 | 9 | BEF | Mediterranean | 2006–09(07) | 593 | 3.5 | Garbulsky et al .(2008), Reichstein et al. (2007) [51,52] |
| 14 | IT-Col | 41.849 | 13.588 | 1645 | BDF | Mediterranean | 2004–07(05) | 954 | 6.4 | Valentini et al. (1996) [53] |
| 15 | US-MOz | 38.744 | −92.200 | 212 | BDF | Mediterranean | 2004–08(05) | 1023 | 4.0 | Gu et al. (2006) [54] |
| 16 | CA-Oas | 53.629 | −106.198 | 580 | BDF | Boreal | 2001–05(03) | 261 | 2.6 | Barr et al. (2007), Krishnan et al. (2006) [55,56] |
| 17 | DK-Sor | 55.487 | 11.646 | 40 | BDF | Boreal | 2003–05, 2008–09(04) | 631 | 5.0 | Pilegaard et al. (2003) [57] |
| 18 | CA-Mer | 45.409 | −75.519 | 65 | BDS | Temperate | 2004–07(06) | 1203 | 1.2 | Lafleur et al. (2003), Roulet et al. (2007) [58,59] |
| 19 | CA-NS6 | 55.917 | −98.964 | 271 | BDS | Boreal | 2002–06(02) | 267 | 3.0 d | Goulden et al. (2006), McMillan et al. (2008) [60,61] |
| 20 | AT-Neu | 47.116 | 11.320 | 970 | GRA | Temperate | 2002–07(03) | 764 | 6.5 | Wohlfahrt et al. (2008) [62] |
| 21 | IE-Dri | 51.987 | −8.752 | 187 | GRA | Temperate | 2002–06(04) | 1341 | 5.2 c | Montaldo et al. (2007), Peichl et al. (2010) [63,64] |
| Biome Types | Climate Zones | LUEdef | LUE | LUE-SW | Farquhar |
|---|---|---|---|---|---|
| ɛmax b (gC·MJ−1) | ɛmax (gC·MJ−1) | ɛmax (gC·MJ−1) | (μmol·m−2·s−1) | ||
| NEF | Temperate | 0.96 | 1.01(±0.15) c | 1.08(±0.13) | 46.69 ± (4.79) |
| NEF | Boreal | 0.96 | 0.78(±0.18) | 0.85(±0.24) | 40.70 ± (2.14) |
| NDF | Boreal | 1.09 | 0.85(±0.22) | 1.02(±0.02) | 25.28 ± (2.81) |
| BEF | Temperate | 1.27 | 0.81(±0.09) | 1.00(±0.09) | 40.81 ± (4.03) |
| BDF | Temperate | 1.17 | 0.99(±0.19) | 1.02(±0.14) | 32.21 ± (3.09) |
| BDF | Boreal | 1.17 | 1.70(±0.03) | 1.73(±0.06) | 37.55 ± (1.22) |
| BDS | Temperate | 0.84 | 1.65 | 1.65 | 26.21 |
| BDS | Boreal | 0.84 | 0.54 | 0.71 | 21.58 |
| GRA(C3) | Temperate | 0.86 | 1.31(±0.12) | 1.32(±0.10) | 26.33(±2.03) |
| Overall | 1.01(±0.12) | 1.05(±0.33) | 1.13(±0.29) | 37.16(±9.48) | |
| Parameter Differences | |||||
| PFTs | - | <0.001 | <0.001 | <0.001 | |
| Biome types | - | 0.233 | 0.388 | 0.002 | |
| Climate zones | 0.791 | 0.824 | 0.953 | 0.127 | |
| Months/Seasons | MOD17A2 | LUE | LUE-SW | Farquhar | ||||
|---|---|---|---|---|---|---|---|---|
| Bias | RMSE | Bias | RMSE | Bias | RMSE | Bias | RMSE | |
| Jan. | −0.28(±0.43) a | 0.42(±0.39) | −0.36(±0.56) | 0.49(±0.54) | −0.31(±0.46) | 0.43(±0.47) | −0.26(±0.45) | 0.43(±0.44) |
| Feb. | −0.18(±0.48) | 0.42(±0.43) | −0.18(±0.65) | 0.56(±0.54) | −0.15(±0.54) | 0.47(±0.49) | −0.12(±0.59) | 0.49(±0.47) |
| Mar. | −0.28(±0.98) | 0.81(±0.78) | −0.11(±0.91) | 0.81(±0.61) | −0.09(±0.57) | 0.57(±0.42) | 0.15(±0.95) | 0.80(±0.74) |
| Apr. | −0.15(±1.91) | 1.53(±1.31) | 0.31(±1.28) | 1.22(±0.77) | 0.37(±0.98) | 1.01(±0.62) | 0.76(±1.19) | 1.30(±0.87) |
| May | −0.39(±2.66) | 2.36(±1.69) | −0.62(±1.30) | 1.59(±0.96) | −0.42(±1.35) | 1.58(±0.95) | 0.68(±1.35) | 1.48(±0.95) |
| Jun. | −0.49(±3.08) | 2.68(±2.00) | −1.52(±1.33) | 2.06(±1.10) | −1.45(±1.21) | 1.80(±1.09) | 0.19(±1.30) | 1.45(±1.02) |
| Jul. | −0.33(±3.06) | 2.70(±1.76) | −1.71(±1.38) | 2.02(±1.17) | −1.69(±1.30) | 1.92(±1.06) | −0.36(±1.21) | 1.42(±0.62) |
| Aug. | 0.08(±2.44) | 2.16(±1.48) | −1.18(±1.29) | 1.62(±0.97) | −1.03(±1.14) | 1.53(±0.85) | −0.54(±0.92) | 1.23(±0.54) |
| Sep. | −0.04(±1.75) | 1.61(±1.07) | −0.71(±0.85) | 1.19(±0.54) | −0.82(±0.95) | 1.30(±0.62) | −0.38(±1.10) | 1.16(±0.72) |
| Oct. | −0.28(±1.03) | 0.93(±0.65) | −0.45(±0.88) | 0.87(±0.60) | −0.43(±0.90) | 0.88(±0.61) | −0.11(±1.21) | 0.96(±0.83) |
| Nov. | −0.22(±0.52) | 0.51(±0.38) | −0.19(±0.66) | 0.63(±0.45) | −0.15(±0.65) | 0.61(±0.46) | 0.00(±0.71) | 0.60(±0.52) |
| Dec. | −0.08(±0.58) | 0.39(±0.47) | −0.08(±0.46) | 0.38(±0.37) | −0.06(±0.51) | 0.38(±0.43) | 0.03(±0.55) | 0.39(±0.45) |
| Winter b | −0.18(±0.44) | 0.43(±0.40) | −0.20(±0.42) | 0.52(±0.44) | −0.17(±0.35) | 0.77(±0.38) | −0.12(±0.34) | 0.47(±0.42) |
| Spring | −0.21(±0.98) | 1.02(±0.81) | −0.02(±0.78) | 0.95(±0.51) | 0.01(±0.47) | 2.05(±0.98) | 0.22(±0.69) | 0.96(±0.58) |
| Summer | −0.40(±2.71) | 2.66(±1.70) | −1.28(±1.00) | 1.96(±0.96) | −1.21(±0.88) | 1.57(±0.70) | 0.17(±0.90) | 1.54(±0.69) |
| Fall | −0.06(±1.59) | 1.81(±0.95) | −0.81(±0.66) | 1.36(±0.60) | −1.08(±0.68) | 0.47(±0.42) | −0.36(±0.80) | 1.21(±0.54) |
| All year | −0.22(±1.25) | 1.78(±0.96) | −0.59(±0.37) | 1.38(±0.51) | −0.66(±0.38) | 0.43(±0.47) | −0.01(±0.47) | 1.18(±0.44) |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, J.; Zhang, H.; Liu, Z.; Che, M.; Chen, B. Evaluating Parameter Adjustment in the MODIS Gross Primary Production Algorithm Based on Eddy Covariance Tower Measurements. Remote Sens. 2014, 6, 3321-3348. https://doi.org/10.3390/rs6043321
Chen J, Zhang H, Liu Z, Che M, Chen B. Evaluating Parameter Adjustment in the MODIS Gross Primary Production Algorithm Based on Eddy Covariance Tower Measurements. Remote Sensing. 2014; 6(4):3321-3348. https://doi.org/10.3390/rs6043321
Chicago/Turabian StyleChen, Jing, Huifang Zhang, Zirui Liu, Mingliang Che, and Baozhang Chen. 2014. "Evaluating Parameter Adjustment in the MODIS Gross Primary Production Algorithm Based on Eddy Covariance Tower Measurements" Remote Sensing 6, no. 4: 3321-3348. https://doi.org/10.3390/rs6043321
APA StyleChen, J., Zhang, H., Liu, Z., Che, M., & Chen, B. (2014). Evaluating Parameter Adjustment in the MODIS Gross Primary Production Algorithm Based on Eddy Covariance Tower Measurements. Remote Sensing, 6(4), 3321-3348. https://doi.org/10.3390/rs6043321