1. Introduction
As a newly arisen space geodetic technique, synthetic aperture radar interferometry (InSAR) is well known as an effective and powerful tool for monitoring land deformation. By analyzing the temporal deformation behavior using time series of phase signals, multi-temporal InSAR is able to mitigate the negative effects of two major limitations in conventional InSAR for deformation tracking,
i.e., spatiotemporal decorrelation and atmospheric artifacts [
1,
2,
3,
4]. In the past decade, several advanced approaches to multi-temporal InSAR have been proposed to adapt to the specific applications, including permanent scatterer interferometry [
1,
2], small baseline subset method [
3], coherent pixel technique [
4], persistent scatterer interferometry (PSI) [
5,
6], persistent scatterer (PS) networking analysis [
7,
8,
9,
10], and temporarily coherent point InSAR [
11].
Previous investigations indicate that the PS networking approach has advantages in eliminating geometric inconsistency and raising quality of deformation measurements, e.g. [
7,
8,
9,
10,
11]. The network, formed by using all the PSs in a study area, contains a number of connections (
i.e., arcs) between adjacent PSs. Therefore, the differential modeling of phase data can be implemented for every arc to cancel out or decrease the impact of spatially-correlated atmospheric delay and other systematic errors [
7,
8,
9,
10], thus benefiting deformation extraction by a least squares (LS) estimator. As shown in
Figure 1, several types of PS networks, including star network, minimum spanning tree (MST) network, triangular irregular network (TIN), and freely connected network (FCN), have been used for differential modeling and time-series deformation analysis. For the above four types of network, the former two types (
i.e., star and MST) are relatively simple and cannot be used for the LS-based estimation, while the latter two types (
i.e., TIN and FCN) with the redundant connections and differential phases can be used for the LS-based estimation [
4,
7,
8,
9,
10,
11,
12,
13,
14]. It is understood that more connections between adjacent PSs in a network can result in a more reliable solution of deformation measurements by the LS adjustment, but decreases computational efficiency. High density of PSs for deformation analysis benefits from high-resolution SAR imagery (e.g., TerraSAR-X and COSMO-SkyMed data) [
9], but the computer time and memory requirements increase significantly for the LS-based PS solution.
To balance between computational efficiency and solution accuracy, this paper presents a hierarchical approach to PS networking and solution for deformation analysis using a time series of high-resolution satellite SAR images. We propose a dividing and conquering algorithm for estimating deformation rates at all the PSs in the area of interest, in which two levels of PS network construction and LS-based solution are performed, and the results derived from the first-level analysis are used as the reference data for the second-level analysis. All the PSs in the imaged area are first divided into multiple subsets by gridding division. For the first-level solution, a global control network (GCN) is constructed by using the feature PSs in each grid cell (see
Section 2.2.1). The feature PSs mean having high signal-to-noise ratio (SNR) in phase measurements and they are empirically selected as the primary control points (PCPs) for estimating deformation rates at the PCPs by a LS-based solution. For the second-level solution, the PSs in each grid cell are used to form a localized triangular irregular network (LTIN) for estimating deformation rates at all PSs through a LS solution by taking the PCPs in the grid cell as reference points. The algorithm will be tested using 40 high-resolution TerraSAR-X (TSX) images collected by SpotLight mode between March 2009 and December 2010 over Tianjin in China for subsidence analysis, and validated by using ground-based leveling measurements obtained at seven leveling benchmarks (BM) and six man-made corner reflectors (CR). In terms of both computing time and memory required for PS solution, the results derived by the hierarchical method will be compared with those derived by a conventional method,
i.e., a single level of TIN-based solution.
Figure 1.
Several typical PS networks used elsewhere, including star network, minimum spanning tree (MST) network, triangular irregular network (TIN), and freely connected network (FCN).
Figure 1.
Several typical PS networks used elsewhere, including star network, minimum spanning tree (MST) network, triangular irregular network (TIN), and freely connected network (FCN).
2. Methodology
Unlike the methodology for a single level of PS networking and solution as described in [
7,
8], a novel hierarchical approach will be described in this section for estimating deformation rates by using time series of high-resolution satellite SAR images. The deformation rates at all the PSs can be estimated by a dividing and conquering algorithm, in which the two levels of PS networking and LS-based solution are performed, and the results derived from the first-level network are used as the reference data for the second-level network. This investigation mainly concentrates on estimating the linear deformation rates. The procedures for estimating nonlinear deformation can still be applied by following the method as described in [
7], which will not be repeatedly presented here.
2.1. Gridding Division of Persistent Scatterers
The grid size for partition of PSs should be determined reasonably to make the data quantity be moderate for two levels of PS networking. We determine the grid size by using the following equation:
where
S stands for the grid size,
for the averaged PS density of the imaged area, and
N for the objective number of PSs in each grid cell (see
Section 4.1), which can be used as a criterion for determining the grid size.
For better understanding,
Figure 2 shows an example of gridding division of the 5000 PSs simulated for an area with a size of 400 × 400 pixels and the averaged PS density
of 1/32. If expecting the number
N of PSs in each grid cell to be 100, one can simply infer by (1) that the grid size
S should be of 6400 pixels,
i.e., a square of 80 × 80 pixels. As shown in
Figure 2, the imaged area is therefore divided into 5 × 5 grid cells.
Figure 2.
An example of the global control network (GCN) and the localized triangular irregular networks (LTINs) constructed with the 5000 PSs (marked by dark dots) simulated for an area with a size of 400×400 pixels. A primary control point (PCP, marked by a filled green square) is selected for each grid, and the PCPs in adjacent grids are linked by the transition PCPs (marked by black circles), thus forming the GCN (marked by black lines). All the PSs in each grid are connected to form the LTIN (marked by gray lines).
Figure 2.
An example of the global control network (GCN) and the localized triangular irregular networks (LTINs) constructed with the 5000 PSs (marked by dark dots) simulated for an area with a size of 400×400 pixels. A primary control point (PCP, marked by a filled green square) is selected for each grid, and the PCPs in adjacent grids are linked by the transition PCPs (marked by black circles), thus forming the GCN (marked by black lines). All the PSs in each grid are connected to form the LTIN (marked by gray lines).
2.2. Global Control Network Construction and Least Squares Solution
As mentioned previously, the two levels of PS networks, i.e., global control network (GCN) and localized triangular irregular network (LTIN), are constructed for estimating deformation rates. The former consists of the feature PSs selected from all the grid cells, while the latter consists of all the PSs in each grid cell. Such feature PSs are termed the primary control points (PCPs), which should be evenly distributed in the entire study area. Deformation rates at the PCPs can be estimated using LS adjustment.
2.2.1. Primary Control Point Selection and Global Control Network Construction
The PCPs are selected by considering two aspects,
i.e., high SNR in phase measurements and proper location. For each grid cell, a representative PS is first selected as a core PCP that should have the smallest amplitude dispersion index [
2] and the shortest distance to the center of the grid cell. The selection process for the core PCP can be represented by:
where
ADIi stands for the amplitude dispersion index of the
ith PS (
i = 1, 2, …,
n) in the grid cell,
n for the total number of PSs in the grid cell, and
Di for the distance between the grid center and the location of the
ith PS.
Considering that atmospheric delay varies quickly in space domain, the shorter distance between neighboring PCPs means a higher spatial correlation for neighborhood differential modeling. As the separation between two adjacent core PCPs is generally too large, we add some transition PCPs to shorten the distance.
The transition PCPs should be determined using some definite criteria. Here we propose a two-step method for choosing the transition PCPs. As an example,
Figure 3 shows how the transition PCPs between the two core PCPs (
i.e., A and B) are identified properly. The first step is to set a boundary (
i.e., blue lines in
Figure 3) around the line AB (a band of 30 pixels used for this example), and the PSs within the boundary and located nearest to the line AB in each normal direction are chosen as the initial candidates of transition PCPs. The second step is to further discard some candidates through removing some very short arcs by using a distance threshold (30 pixels used for this example), thus obtaining the final transition PCPs. The points and connections derived by the two steps can be exemplified by
Figure 3a and b, respectively. It can be seen from this example that four PSs are eventually selected as the transition PCPs from 11 PSs (
i.e., the initial candidates for transition PCPs) through the two-step selection process.
It should be noted that there is only a core PCP for each grid (marked by a filled green square in
Figure 2), and the transition PCPs (marked by black circles in
Figure 2) between any two core PCPs from two adjacent grids should be identified using the procedures described above. Once both the core and transition PCPs are identified, they generally distribute along the longitudinal and transverse directions. We connect the two types of PCPs by minimizing the accumulative distance between adjacent PCPs, thus forming a grid-like network that is referred to as the GCN. As an example,
Figure 2 shows the GCN constructed by using the core PCPs and transition PCPs selected from the simulated data. As a remark, special treatment should be given to the grids at the margin of the imaged area or other grids where only few PSs are available due to localized temporal decorrelation. If the total number of PSs in a grid is not greater than 4, all the PSs are chosen as the core or transition PCPs. If a grid is located at the image margin, the connections between the PCPs may be very weak (e.g., long arcs), thus resulting in some isolated arcs and PCPs. Therefore, we connect those PCPs to the core or transition PCPs in the adjacent grids, thus forming a closed path for further analysis. As an example,
Figure 4 demonstrates such special treatment for constructing a GCN in the case of few PSs being available for some grids.
Figure 3.
An example of the selection process of the transition primary control points (PCPs). The transition PCPs are selected from all the PSs located in the buffer defined by the blue lines around line AB, as shown in (a) to (b).
Figure 3.
An example of the selection process of the transition primary control points (PCPs). The transition PCPs are selected from all the PSs located in the buffer defined by the blue lines around line AB, as shown in (a) to (b).
Figure 4.
An example of global control network in the case of few PSs being available in several grids. Only one or two PSs are located in the top-left and bottom-right grid, respectively, and there is no PS in the central grid.
Figure 4.
An example of global control network in the case of few PSs being available in several grids. Only one or two PSs are located in the top-left and bottom-right grid, respectively, and there is no PS in the central grid.
2.2.2. Least Squares Solution Based on the Global Control Network
For a PCP with pixel coordinates (
x,
y), the interferometric phase
in the
ith interferogram with temporal baseline
ti can be expressed by [
2]:
where
and
Ti are the perpendicular (spatial) and temporal baselines, respectively;
λ,
R, and
θ are the radar wavelength (3.1 cm for TSX case), the sensor-to-PCP distance, and the radar incidence angle, respectively; and
,
,
and
are the elevation error, linear deformation rate along radar line of sight (LOS), and residual phase, respectively.
For an arc connecting two adjacent PCPs (
l and
p) in the GCN, the differential phase can be derived using Equation (3),
i.e.,
where
,
and
are the mean perpendicular baseline, the mean sensor-to-PCP distance, and the mean incident angle of the two PCPs, respectively; and
and
are the differential elevation error and the differential linear deformation rate between the two PCPs. With
M interferograms generated from
N SAR images,
M observation equations as shown in Equation (4) can be obtained for any arc of the GCN.
By following the methodology proposed by Ferretti
et al. [
1,
2], the unknowns
and
of all the arcs in the GCN can be derived. Then, a LS solution can be applied to the GCN for the purpose of eliminating geometric inconsistency and deriving the most probable values for the deformation rate and elevation error for each PCP. For deformation rate estimation, the observation equation for the deformation rate increment between two adjacent PCPs is:
Where
and
are the deformation rates along radar LOS of the PCP
l and PCP
p, respectively;
is the increment of deformation rates between the two PCPs;
is the residual of
; and
K is the total number of PCPs in the GCN. The matrix form of the observation equations is written as:
where
B is a coefficient matrix;
L and
R are the vectors of the observations (
i.e., deformation rate increments) and the residuals, respectively;
Q is the total number of arcs in the GCN; and
X is the vector of unknown deformation rates to be estimated,
i.e.,
Furthermore, let the weight matrix be
whose diagonal elements are the squares of the model coherence (MC) values previously estimated for the PS pairs. Ferretti
et al. indicate that if
is small enough, say
, it is possible to estimate both
and
directly from the
M wrapped differential interferograms by maximizing the following objective function [
1,
2]:
where
γ is the MC value of the two PS points;
, and
denotes the difference between the measured and the estimated phase values,
Therefore, the LS solution of the unknowns X can be expressed by:
It should be noted that a reference point (e.g., a PCP without any movement or a leveling point with the known deformation rate) needs to be chosen for the LS solution, and the deformation rates of all other PCPs are derived relative to this reference point.
2.3. Localized Triangular Irregular Network Construction and Least Squares Solution
Upon completion of the first level networking and solution, the PCPs can be used as control points with the known deformation rates for the second-level analysis, which is performed on a grid-by-grid basis. For any grid cell, all the PSs (including the PCPs) are connected using the Delaunay triangulation method to form a localized triangular irregular network (LTIN). For the simulated data,
Figure 2 also shows the resultant LTINs for all the grid cells and the associated GCN. It should be emphasized that each individual LTIN is related to the adjacent LTINs by the GCN, and considered as an individual processing unit. The estimation of deformation rates at the non-PCP PSs can be conducted by following the same procedures as described for the GCN-based LS solution in
Section 2.2. The deformation rates at the PCPs derived by the first-level analysis are used as known data in the observation equations, thus providing the reference datum for the second level LS solution.
3. Study Area and Data Source
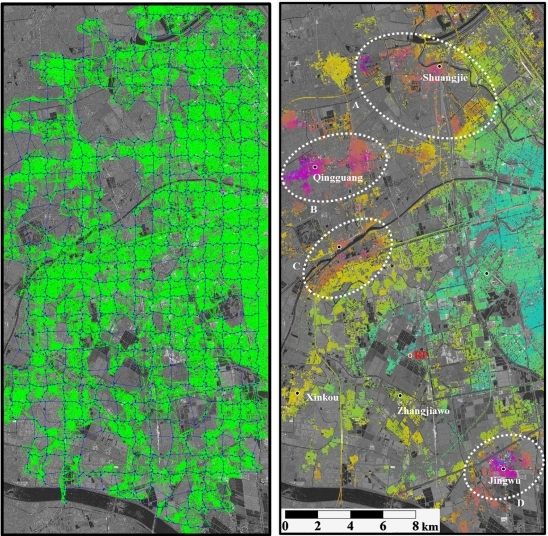
For validation purposes, we selected the northwestern part of Tianjin in China as the study area. As shown in
Figure 5, the study area of 450 km
2 belongs to the alluvial plain of the Haihe River and has very flat relief with a relative elevation difference of 2–3 m [
9]. As one of the biggest cities in China, Tianjin suffers water shortage due to its natural geographic condition and semi-arid climate [
15]. To meet its industrial and agricultural needs, a large amount of groundwater has been exploited in Tianjin since the 1920s, thus resulting in severe land subsidence in many areas [
16]. In recent years, some effective measures such as groundwater injection and restricting or prohibiting groundwater extraction in some planned zones have been taken to mitigate subsidence, and the subsidence rates in urban areas have slowed down to about 10–20 mm/year [
17,
18]. However, serious subsidence is still ongoing around suburban areas and reaches up to 100 mm/year due to overuse of groundwater [
18,
19].
Figure 5.
The location map and the study area around Tianjin in China. The insert at the top-left corner shows the location map and the coverage of the TSX scenes. The left panel shows the amplitude image (averaged from 40 TSX images) in which the study area is marked by the rectangle. The right panel shows the enlarged amplitude image of the study area in which the seven benchmarks (BMs) and six corner reflectors (CRs) are annotated for later analysis.
Figure 5.
The location map and the study area around Tianjin in China. The insert at the top-left corner shows the location map and the coverage of the TSX scenes. The left panel shows the amplitude image (averaged from 40 TSX images) in which the study area is marked by the rectangle. The right panel shows the enlarged amplitude image of the study area in which the seven benchmarks (BMs) and six corner reflectors (CRs) are annotated for later analysis.
For subsidence extraction, we used 40 TSX images acquired by SpotLight mode along descending orbits between 27 March 2009 and 25 December 2010 (all imaging at 6:17 am local time with pixel spacing of 1.36 m in slant range and 1.90 m in azimuth). The 376 interferometric pairs were generated by setting the spatial baseline threshold to 120 m. Although the study area is flat, the SRTM DEM with a spacing of 3 arc sec was used to remove topographic effects from all 376 interferograms. As seen in
Figure 5, the seven BMs and six CRs were used for verification purpose. The four epochs of second-order leveling campaigns (with accuracy of 2 mm/km in height difference) were conducted on both the BMs and the CRs during the period of the TSX acquisitions. The leveling dates for the four epochs are around 20 April 2009, 5 September 2009, 15 April 2010, and 30 October 2010, respectively.
5. Conclusions
For the purpose of balancing between computational efficiency and solution accuracy, this paper presents a hierarchical approach in PSI, i.e., two levels of PS networking and solution, for estimating deformation rates with time series of high-resolution satellite SAR images. For validation purposes, the algorithm was tested using 40 high-resolution TSX images collected by SpotLight mode between 2009 and 2010 over Tianjin in China. The subsidence rates estimated by the hierarchical solution varied between 0 and 110 mm/year in the study area of 450 km2. The subsidence rates in the suburban areas range between 30 and 110 mm/year, which are higher than those (0 to 20 mm/year) in the urban areas. This confirms that subsidence due to ground water extraction is still severe in the suburban areas.
The subsidence rates derived by the leveling and the hierarchical (i.e., GCN-LTINs) PSI solution are comparable at seven BMs and six CRs, and the mean and RMSE of their discrepancies are 0.7 mm/year and ±2.4 mm/year, respectively. The subsidence time series derived from the hierarchical PSI solution is in good agreement with the leveling measurements and those derived from the global-TIN PSI solution. Moreover, the hierarchical method for estimating subsidence rates in the study area raises the computational efficiency and reduces the memory consumption if compared with the method based on the global TIN. It can be concluded that the hierarchical approach proposed in this paper is very suitable for estimating deformation rates even over a huge area with time series of high-resolution SAR images.
It should be pointed out that the relatively weak connections in the GCN used in this study may cause slight jumps in the subsidence rates between neighboring grids. Although the resultant errors are negligible for this study, further investigation should be performed to overcome such drawbacks in the hierarchical approach, thus leaving room for future work.