Monitoring Groundwater Variations from Satellite Gravimetry and Hydrological Models: A Comparison with in-situ Measurements in the Mid-Atlantic Region of the United States
Abstract
:1. Introduction
2. Method and Data
2.1. GRACE-Derived TWS: Data Acquisition and Processing
2.2. Soil Moisture and Snow from GLDAS
2.3. Groundwater from Monitoring Wells

3. Results and Discussion
3.1. Terrestrial Water Storage Variations


| Variables | Annual Amplitude (cm) | Annual Phase (months) | Correlation |
|---|---|---|---|
| GRACE TWS | 8.57 ± 0.59 | 2.90 ± 0.02 | 0.93 |
| SM + SWE + GW | 7.98 ± 0.48 | 2.62 ± 0.02 |
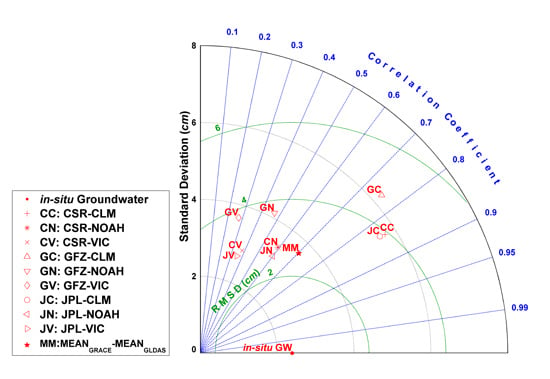
3.2. Intercomparison Analysis of Groundwater Variations



4. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zektser, I.S.; Lorne, E. Groundwater Resources of the World: And Their Use; United Nations Educational, Scientific and Cultural Organization: Paris, France, 2004. [Google Scholar]
- Postel, S. Water and agriculture. In Water in Crisis: A Guide to the World’s Fresh Water Resources; Gleick, P.H., Ed.; Oxford University Press: New York, NY, USA, 1993; pp. 56–66. [Google Scholar]
- Feng, W.; Zhong, M.; Lemoine, J.-M.; Biancale, R.; Hsu, H.-T.; Xia, J. Evaluation of groundwater depletion in North China using the gravity recovery and climate experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef]
- Li, Z.; Muller, J.P.; Cross, P.; Fielding, E.J. Interferometric synthetic aperture radar (InSAR) atmospheric correction: GPS, moderate resolution imaging spectroradiometer (MODIS), and InSAR integration. J. Geophys. Res.: Solid Earth 2005, 110, B03410. [Google Scholar]
- Abdelkareem, M.; El-Baz, F.; Askalany, M.; Akawy, A.; Ghoneim, E. Groundwater prospect map of Egypt’s Qena Valley using data fusion. Int. J. Image Data Fusion 2011, 3, 169–189. [Google Scholar] [CrossRef]
- Luo, Q.; Perissin, D.; Lin, H.; Zhang, Y.; Wang, W. Subsidence monitoring of Tianjin suburbs by TerraSAR-X persistent scatterers interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1642–1650. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S. An analysis of terrestrial water storage variations in Illinois with implications for the gravity recovery and climate experiment (GRACE). Water Resour. Res. 2001, 37, 1327–1339. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J.; Milly, P.C.D. Estimated accuracies of regional water storage variations inferred from the gravity recovery and climate experiment (GRACE). Water Resour. Res. 2003, 39, 1223. [Google Scholar] [CrossRef]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in india. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed]
- Swenson, S.; Wahr, J. Methods for inferring regional surface-mass anomalies from gravity recovery and climate experiment (GRACE) measurements of time-variable gravity. J. Geophys. Res.: Solid Earth 2002. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Rodell, M. Water in the balance. Science 2013, 340, 1300–1301. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Yang, Z.L.; Niu, G.Y. 2005 drought event in the Amazon River basin as measured by GRACE and estimated by climate models. J. Geophys. Res.: Solid Earth 2009, 114, B05404. [Google Scholar]
- Feng, W.; Lemoine, J.-M.; Zhong, M.; Hsu, T.-T. Terrestrial water storage changes in the Amazon basin measured by GRACE during 2002–2010. Chin. J. Geophys.–Chin. Ed. 2012, 55, 814–821. [Google Scholar]
- Frappart, F.; Ramillien, G.; Ronchail, J. Changes in terrestrial water storage versus rainfall and discharges in the Amazon basin. Int. J. Climatol. 2013, 33, 3029–3046. [Google Scholar] [CrossRef] [Green Version]
- Pokhrel, Y.N.; Fan, Y.; Miguez-Macho, G.; Yeh, P.J.F.; Han, S.-C. The role of groundwater in the Amazon water cycle: 3. Influence on terrestrial water storage computations and comparison with GRACE. J. Geophys. Res.: Atmos. 2013, 118, 3233–3244. [Google Scholar] [CrossRef]
- Hu, X.G.; Chen, J.L.; Zhou, Y.H.; Huang, C.; Liao, X.H. Seasonal water storage change of the Yangtze River basin detected by GRACE. Sci. China Ser. D–Earth Sci. 2006, 49, 483–491. [Google Scholar] [CrossRef]
- Ferreira, V.G.; Gong, Z.; He, X.; Zhang, Y.; Andam-Akorful, S.A. Estimating total discharge in the Yangtze River basin using satellite-based observations. Remote Sens. 2013, 5, 3415–3430. [Google Scholar] [CrossRef]
- Crowley, J.W.; Mitrovica, J.X.; Bailey, R.C.; Tamisiea, M.E.; Davis, J.L. Land water storage within the Congo Basin inferred from GRACE satellite gravity data. Geophys. Res. Lett. 2006, 33, L19402. [Google Scholar] [CrossRef]
- Awange, J.L.; Sharifi, M.A.; Ogonda, G.; Wickert, J.; Grafarend, E.W.; Omulo, M.A. The falling lake Victoria water level: GRACE, TRIMM and CHAMP satellite analysis of the lake basin. Water Resour. Manag. 2008, 22, 775–796. [Google Scholar] [CrossRef]
- Velicogna, I. Increasing rates of ice mass loss from the Greenland and Antarctic ice sheets revealed by GRACE. Geophys. Res. Lett. 2009, 36, L19503. [Google Scholar] [CrossRef]
- Wen, H.; Zhu, G.; Cheng, P.; Chang, X.; Liu, H. The ice sheet height changes and mass variations in Antarctica by using ICESAT and GRACE data. Int. J. Image Data Fusion 2011, 2, 255–265. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Zwally, H.J.; Abdalati, W.; Rowlands, D.D.; Ray, R.D.; Nerem, R.S.; Lemoine, F.G.; McCarthy, J.J.; Chinn, D.S. Recent greenland ice mass loss by drainage system from satellite gravity observations. Science 2006, 314, 1286–1289. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. Interannual variability of greenland ice losses from satellite gravimetry. J. Geophys. Res.: Solid Earth 2011, 116, B07406. [Google Scholar]
- Bergmann, I.; Ramillien, G.; Frappart, F. Climate-driven interannual ice mass evolution in greenland. Glob. Planet. Chang. 2012, 82–83, 1–11. [Google Scholar] [CrossRef]
- Jacob, T.; Wahr, J.; Pfeffer, W.T.; Swenson, S. Recent contributions of glaciers and ice caps to sea level rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. Contribution of ice sheet and mountain glacier melt to recent sea level rise. Nat. Geosci. 2013, 6, 549–552. [Google Scholar] [CrossRef]
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating groundwater storage changes in the Mississippi River basin (USA) using GRACE. Hydrogeol. J. 2007, 15, 159–166. [Google Scholar] [CrossRef]
- Tiwari, V.M.; Wahr, J.; Swenson, S. Dwindling groundwater resources in northern India, from satellite gravity observations. Geophys. Res. Lett. 2009, 36, L18401. [Google Scholar] [CrossRef]
- Voss, K.A.; Famiglietti, J.S.; Lo, M.; de Linage, C.; Rodell, M.; Swenson, S.C. Groundwater depletion in the Middle East from GRACE with implications for transboundary water management in the Tigris-Euphrates-Western Iran region. Water Resour. Res. 2013, 49, 904–914. [Google Scholar] [CrossRef] [PubMed]
- Jin, S.; Feng, G. Large-scale global groundwater variations from satellite gravimetry and hydrological models, 2002–2012. Glob. Planet. Chang. 2013, 106, 20–30. [Google Scholar] [CrossRef]
- Klees, R.; Liu, X.; Wittwer, T.; Gunter, B.C.; Revtova, E.A.; Tenzer, R.; Ditmar, P.; Winsemius, H.C.; Savenije, H.H.G. A comparison of global and regional grace models for land hydrology. Surv. Geophys. 2008, 29, 335–359. [Google Scholar] [CrossRef]
- Bonin, J.; Bettadpur, S.; Tapley, B. High-frequency signal and noise estimates of CSR GRACE RL04. J. Geod. 2012, 86, 1165–1177. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Cheng, M.K.; Tapley, B.D. Variations in the Earth’s oblateness during the past 28 years. J. Geophys. Res.: Solid Earth 2004. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res.: Solid Earth 2008, 113, B08410. [Google Scholar]
- Paulson, A.; Zhong, S.; Wahr, J. Inference of mantle viscosity from GRACE and relative sea level data. Geophys. J. Int. 2007, 171, 497–508. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Grand, S. GRACE detects coseismic and postseismic deformation from the Sumatra-Andaman earthquake. Geophys. Res. Lett. 2007. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Longuevergne, L.; Yang, Z.L.; Scanlon, B.R. Recent La Plata basin drought conditions observed by satellite gravimetry. J. Geophys. Res.: Atmos. 2010. [Google Scholar] [CrossRef]
- Swenson, S.; Yeh, P.J.F.; Wahr, J.; Famiglietti, J. A comparison of terrestrial water storage variations from GRACE with in situ measurements from Illinois. Geophys. Res. Lett. 2006. [Google Scholar] [CrossRef]
- Duan, X.J.; Guo, J.Y.; Shum, C.K.; van der Wal, W. On the postprocessing removal of correlated errors in GRACE temporal gravity field solutions. J. Geod. 2009, 83, 1095–1106. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res.: Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Chao, B.F. On inversion for mass distribution from global (time-variable) gravity field. J. Geodyn. 2005, 39, 223–230. [Google Scholar] [CrossRef]
- Han, D.; Wahr, J. The viscoelastic relaxation of a realistically stratified earth, and a further analysis of postglacial rebound. Geophys. J. Int. 1995, 120, 287–311. [Google Scholar] [CrossRef]
- Andam-Akorful, S.A.; Ferreira, V.G.; Awange, J.L.; Forootan, E.; He, X.F. Multi-model and multi-sensor estimations of evapotranspiration over the Volta Basin, West Africa. Int. J. Climatol. 2014. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48, W04531. [Google Scholar] [CrossRef]
- Jin, S.G.; Hassan, A.A.; Feng, G.P. Assessment of terrestrial water contributions to polar motion from GRACE and hydrological models. J. Geodyn. 2012, 62, 40–48. [Google Scholar] [CrossRef]
- Dai, Y.J.; Zeng, X.B.; Dickinson, R.E.; Baker, I.; Bonan, G.B.; Bosilovich, M.G.; Denning, A.S.; Dirmeyer, P.A.; Houser, P.R.; Niu, G.Y.; et al. The common land model. Bull. Am. Meteorol. Soc. 2003, 84, 1013–1023. [Google Scholar] [CrossRef]
- Shamsudduha, M.; Taylor, R.G.; Longuevergne, L. Monitoring groundwater storage changes in the highly seasonal humid tropics: Validation of GRACE measurements in the bengal basin. Water Resour. Res. 2012, 48, W02508. [Google Scholar]
- Cunningham, W.L.; Geiger, L.H.; Karavitis, G.A.U.S. Geological Survey Ground-Water Climate Response Network. Available online: http://pubs.usgs.gov/fs/2007/3003/pdf/2007-3003-hires.pdf (accessed on 9 January 2015).
- Fetter, C.W. Applied Hydrogeology, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Sun, A.Y.; Green, R.; Rodell, M.; Swenson, S. Inferring aquifer storage parameters using satellite and in situ measurements: Estimation under uncertainty. Geophys. Res. Lett. 2010. [Google Scholar] [CrossRef]
- Heath, R.C. Basic Ground-Water Hydrology. Available online: http://pubs.er.usgs.gov/publication/wsp2220 (accessed on 9 January 2015).
- Joseph, R.L.; Eberts, S.M. Selected Data on Characteristics of Glacial-Deposit and Carbonate-Rock Aquifers, Midwestern Basins and Arches Region. Available online: http://pubs.er.usgs.gov/publication/ofr93627 (accessed on 9 January 2015).
- Syed, T.H.; Famiglietti, J.S.; Rodell, M.; Chen, J.; Wilson, C.R. Analysis of terrestrial water storage changes from grace and gldas. Water Resour. Res. 2008, 44, W02433. [Google Scholar] [CrossRef]
- Shum, C.K.; Guo, J.-Y.; Hossain, F.; Duan, J.; Alsdorf, D.E.; Duan, X.-J.; Kuo, C.-Y.; Lee, H.; Schmidt, M.; Wang, L. Inter-annual water storage changes in Asia from GRACE data. In Climate Change and Food Security in South Asia; Springer: Dordrecht, The Netherlands, 2011; pp. 69–83. [Google Scholar]
- NOAA. State of the Climate: Drought for September 2007; NOAA National Climatic Data Center: Asheville, NC, USA, 2007. [Google Scholar]
- Houborg, R.; Rodell, M.; Li, B.; Reichle, R.; Zaitchik, B.F. Drought indicators based on model-assimilated gravity recovery and climate experiment (GRACE) terrestrial water storage observations. Water Resour. Res. 2012, 48, W07525. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res.: Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Tang, Q.; Zhang, X.; Tang, Y. Anthropogenic impacts on mass change in North China. Geophys. Res. Lett. 2013, 40, 3924–3928. [Google Scholar] [CrossRef]
- Longuevergne, L.; Scanlon, B.R.; Wilson, C.R. Grace hydrological estimates for small basins: Evaluating processing approaches on the high plains aquifer, USA. Water Resour. Res. 2010, 46, W11517. [Google Scholar] [CrossRef]
- Sakumura, C.; Bettadpur, S.; Bruinsma, S. Ensemble prediction and intercomparison analysis of grace time-variable gravity fieldmodels. Geophys. Res. Lett. 2014, 41, 1389–1397. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar]
- Kendall, M.G. Rank Correlation Measures; Griffin: London, UK, 1955. [Google Scholar]
- Kenny, J.F.; Barber, N.L.; Hutson, S.S.; Linsey, K.S.; Lovelace, J.K.; Maupin, M.A. Estimated Use of Water in the United States in 2005. Available online: http://pubs.usgs.gov/circ/1344/ (accessed on 9 January 2015).
- Wahr, J.; Swenson, S.; Velicogna, I. Accuracy of grace mass estimates. Geophys. Res. Lett. 2006, 33, L06401. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, R.; He, X.; Zhang, Y.; Ferreira, V.G.; Chang, L. Monitoring Groundwater Variations from Satellite Gravimetry and Hydrological Models: A Comparison with in-situ Measurements in the Mid-Atlantic Region of the United States. Remote Sens. 2015, 7, 686-703. https://doi.org/10.3390/rs70100686
Xiao R, He X, Zhang Y, Ferreira VG, Chang L. Monitoring Groundwater Variations from Satellite Gravimetry and Hydrological Models: A Comparison with in-situ Measurements in the Mid-Atlantic Region of the United States. Remote Sensing. 2015; 7(1):686-703. https://doi.org/10.3390/rs70100686
Chicago/Turabian StyleXiao, Ruya, Xiufeng He, Yonglei Zhang, Vagner G. Ferreira, and Liang Chang. 2015. "Monitoring Groundwater Variations from Satellite Gravimetry and Hydrological Models: A Comparison with in-situ Measurements in the Mid-Atlantic Region of the United States" Remote Sensing 7, no. 1: 686-703. https://doi.org/10.3390/rs70100686
APA StyleXiao, R., He, X., Zhang, Y., Ferreira, V. G., & Chang, L. (2015). Monitoring Groundwater Variations from Satellite Gravimetry and Hydrological Models: A Comparison with in-situ Measurements in the Mid-Atlantic Region of the United States. Remote Sensing, 7(1), 686-703. https://doi.org/10.3390/rs70100686