Estimation of Land Surface Temperature under Cloudy Skies Using Combined Diurnal Solar Radiation and Surface Temperature Evolution

Abstract

Land surface temperature (LST) is a key parameter in the interaction of the land-atmosphere system. However, clouds affect the retrieval of LST data from thermal-infrared remote sensing data. Thus, it is important to determine a method for estimating LSTs at times when the sky is overcast. Based on a one-dimensional heat transfer equation and on the evolution of daily temperatures and net shortwave solar radiation (NSSR), a new method for estimating LSTs under cloudy skies (T_cloud) from diurnal NSSR and surface temperatures is proposed. Validation is performed against in situ measurements that were obtained at the ChangWu ecosystem experimental station in China. The results show that the root-mean-square error (RMSE) between the actual and estimated LSTs is as large as 1.23 K for cloudy data. A sensitivity analysis to the errors in the estimated LST under clear skies (T_clear) and in the estimated NSSR reveals that the RMSE of the obtained T_cloud is less than 1.5 K after adding a 0.5 K bias to the actual T_clear and 10 percent NSSR errors to the actual NSSR. T_cloud is estimated by the proposed method using T_clear and NSSR products of MSG-SEVIRI for southern Europe. The results indicate that the new algorithm is practical for retrieving the LST under cloudy sky conditions, although some uncertainty exists. Notably, the approach can only be used during the daytime due to the assumption of the variation in LST caused by variations in insolation. Further, if there are less than six T_clear observations on any given day, the method cannot be used.

1. Introduction

Land surface temperature (LST) is an important variable in many research areas, such as global climate change, retrieval of soil moisture content, and ground flux [1,2]. Remote sensing is an effective way of providing LSTs at the regional and global scales. Remote sensors with infrared channels, such as the Moderate-resolution imaging Spectrometer (MODIS) and the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER), play important roles in estimating LST. Currently, four major TIR-based LST retrieval methods have been developed, including the single-channel method, the split-window method, the multi-angle method and the multi-temporal method; the accuracy of most methods is within 1 K [3,4].

Most studies focus on cloud-free conditions. However, on a regional scale, the actual weather is cloudy in most regions for more than half of the year [5]. The presence of clouds significantly modifies the surface energy budget [6]. Many land surface temperature products from existing satellite remote sensing data only detect cloud pixels without recording the pixel’s temperature; thus, LST data are lacking in cloudy areas. However, many studies concerning the application of these data (such as drought monitoring, vegetation growth and crop yield estimation) need the entire spatial distribution of the LST over a region. Therefore, LST estimates under cloudy skies (T_cloud) are urgently needed. Because of the absorption of surface emission by clouds, T_cloud cannot be calculated directly from remotely sensed thermal-infrared information. Presently, only microwave remote sensing can be used to obtain T_cloud because it is able to penetrate clouds. Jia et al. [7] retrieved LST data based on passive-microwave remotely sensed data and achieved an accuracy of 3 K relative to the MODIS LST product. However, these methods of using microwave observations are limited because microwave remote sensing is very sensitive to surface roughness and surface moisture.

On the basis of the surface energy balance, Jin et al. [6] proposed a “neighboring-pixel” approach to estimate the LST of cloudy pixels from polar-orbiting satellite data, in which the LST of a cloudy pixel is interpolated from LST observations of surrounding clear sky (T_clear) pixels within 100–300 Km or within two days. The method is limited if the clear and cloudy pixels are not homogeneous and the atmospheric conditions are non-uniform. To overcome this weakness, Lu et al. [8] calculated T_cloud, which is interpolated from temporal-based neighboring-pixel T_clear observations and is compared using the spatial-based neighboring-pixel method. The result shows that the temporal “neighboring-pixel” method is better than a spatial approach, and the absolute error is within 1.5 K. However, one disadvantage of this approach is inevitable. Specifically, T_cloud is interpolated from T_clear of temporally neighboring pixels, while the difference in net solar shortwave radiation (NSSR) in the proposed method is obtained from spatially neighboring pixels.

The objective of this study is to estimate the LST under cloudy skies from multi-temporal remote sensing observations. The methodology is presented in Section 2, and the data, including satellite and ground-based measurements, are described in Section 3. The results and discussions of the proposed method are presented in Section 4. Section 5 provides an example of estimating LST under overcast conditions from Meteosat Second Generation (MSG)/SEVIRI data. Finally, the conclusion is presented in Section 6.

2. Method

Assuming the 1D periodic heating of a uniform half-space of constant thermal properties, the temperature obeys the diffusion equation:

$$\frac{\partial T}{\partial t}=k\frac{{\partial }^{2}T}{\partial z^2}$$

(1)

where k is thermal diffusivity (m²∙s⁻¹) and T(z,t) represents the soil temperature at a distance (z) below the surface at time (t). Under a specific set of initial and boundary conditions, the model gives the surface-subsurface temperature profiles as a function of time. Initial conditions are specified 24 h or more before the time to weaken the dependence of the model results on initial values. The lower boundary condition is that the temperature is constant at a depth of 50 cm and the upper boundary condition is the energy balance equation which is listed as Equation (2) [9].

$$NSSR+L_{net}+H+LE+G=0$$

(2)

where NSSR is the net shortwave solar radiation (W∙m⁻²), L_net is the net longwave radiation from ground and air (W∙m⁻²), H is sensible heat transfer between ground and air (W∙m⁻²), LE is the latent heat transfer between ground and air (W∙m⁻²) and G is heat conducted in the soil or rock unit (W∙m⁻²).

A solution to Equation (1) using the cosine function is

$$T(z,t)=\overline{T}+T_0\text{cos}(w(t-t_d)-z/\text{δ})\text{exp}(-z/\text{δ})$$

(3)

where $\text{δ}=\sqrt{2k\text{/}w}$ is the damping depth of the diurnal temperature wave, t_d is the time at which the surface temperature (z = 0) reaches its maximum and w is the angular diurnal frequency of surface temperature in a period (which is nearly π/DD (DD is the duration of daytime)).

Combining Equation (3), the ground G (z = 0) heat transport in Equation (2), which is defined as positive in the downward direction, can be written as

$$G(z=0)=-K\frac{\partial T}{\partial z}=P{T}_0\sqrt{w}\text{cos}(w(t-t_d)+\frac{\text{π}}{4})$$

(4)

where K is the thermal conductivity (W∙m⁻¹∙K⁻¹), P is the thermal inertia (W∙s^1/2∙m⁻²∙k⁻¹) and the other parameters are the same as those in Equation (3).

Equation (2) can be also written as:

$$G=Rn-H-LE=(1-A)S\mathit{\tau }\text{cos}(Zn)-{\text{ε}}_s\text{σ}{T}^4+L_{atm\downarrow }-H-LE$$

(5)

where

$$\begin{array}{l}{R}_n=NSSR+L_{net}\\ NSSR=(1-A)S\mathit{\tau }\text{cos}(Zn)\\ L_{net}=L_{at{m}_{\downarrow }}-{\text{ε}}_s\text{σ}{T}^4\\ \text{cos}(Zn)=\text{cos}(\text{λ})\text{cos}({\text{δ}}_s)\text{cos}(w_1(t-t_s))+\text{sin}(\text{λ})\text{sin}({\text{δ}}_s)\end{array}$$

where S is the solar constant, τ is the transmission, A is the broadband albedo, Zn is the solar zenith, R_n is the net radiation (W∙m⁻²), ε_s is the surface emissivity, L_atm↓ is the atmospheric downward radiation, λ is the latitude, δ_s is the solar declination angle, NSSR is the net shortwave solar radiation (W∙m⁻²), w₁ is the angular diurnal frequency of solar radiation in a period that is nearly π/DD (DD is the duration of daytime), t_s is the time (local time 12 h in general) at which the NSSR is maximized (NSSR_max).

According to Equation (5), NSSR can be expressed as:

$$NSSR=(1-A)S\text{τ}\times [\text{cos}(\text{λ})\text{cos}({\text{δ}}_s)\text{cos}(w_1(t-t_s))+\text{sin}(\text{λ})\text{sin}({\text{δ}}_s)]=S_{\text{min}}+S_{\text{max}}\times \text{cos}(w_1(t-t_s))$$

(6)

where: in theory, S_min = (1 − A)S τsin(λ)sin(δ_s), approximately represents the minimum daytime NSSR, and S_max = (1 − A)S τcos(λ)cos(δ_s), approximately represents amplitude of the daytime NSSR, w₁ and t_s are the same as those in Equation (5).

Just as shown in Equation (6), if A and τ are stable over a day, then a harmonic variation (cosine function) can be used to describe the diurnal NSSR evolution exactly. Note, the surface is not a Lambertian reflector, i.e., the albedo is related to the solar zenith angle, and the transmittance (τ) is not constant over a day. However, A and τ are relative stable to incoming solar radiation, and diurnal NSSR in the daytime can be only approximately described with four parameters (S_min, S_max, w₁ and t_s), we defined the model as diurnal solar cycle model (DSC).

According to Equation (3), the surface temperature can be written as

$$T(0,t)=\overline{T}+T_0\text{cos}(w(t-t_d))$$

(7)

Many researchers think the cosine function can only be used to describe the daytime LST, and an exponential attenuation function can be employed to fit the nighttime LST [10,11,12]; thus, the diurnal evolution of the LST (DTC) can be written as

$$T\left(t\right)=\{\begin{array}{l}\overline{T}+T_0\text{cos}(w(t-t_d)),(t<t_{rs})\\ b_1+b_2\exp (\text{β}(t-t_{rs})),(t\ge t_{rs})\end{array}$$

(8)

where

$$\begin{gathered} b_2=-T_{0}w\text{sin}w(t_{rs}-t_d)/\beta \\ {b}_1=\overline{T}+T_0\text{cos}w(t_{rs}-t_d)-b_2 \end{gathered}$$

Moreover, T and T₀ are the two parameters to be defined: approximately represents the minimum temperature (T_min), while T₀ represents the amplitude (approximately T_max − T_min, where T_max is the maximum daytime LST). Furthermore, t_rs is the starting time of the attenuation (near sunset), β is the decay coefficient during the nighttime, t_d and w are the same as those in Equation (3).

Assuming that L_atm↓ − H – LE = aT + b and that the surface longwave radiation function is linearized in the vicinity (T_i), the following function can be derived by simple mathematical manipulation of Equations (4)–(6):

$$G=S \text{min}+S \text{max}\times \text{cos}(w_1\times (t-t_s))+3\times \mathit{\epsilon }\mathit{\sigma }{T}_i^4+b+(a-4\mathit{\epsilon }\mathit{\sigma }{T}_i^3)T=P{T}_0\sqrt{w}\text{cos}(w(t-t_d)+\frac{\text{π}}{4})$$

(9)

Assuming w₁ is the same as w in Equation (9), i.e., w₁ = w, and substituting Equation (7) into Equation (9), the daytime surface temperature (T) can be expressed as follows:

$$T=-\frac{D}{E}+\frac{S\text{max}}{\sqrt{w{P}^2+\sqrt{2w}EP+E^2}}\text{cos}(w(t-(t_d-t_s)))$$

(10)

where,

$$\begin{array}{c}D=b+3\epsilon \sigma T_i^4+S \text{min}\\ E=4\epsilon \sigma T_i^3-a\\ tg(w·(t_d-t_s))=\frac{P\sqrt{w}}{\sqrt{2}E+P\sqrt{w}}\end{array}$$

and

$$T_0=\frac{S\text{max}}{\sqrt{w{P}^2+\sqrt{2w}EP+E^2}}$$

(11)

The method used to estimate the thermal inertia can be obtained by combining tg(w × (t_d − t_s)) with T₀ as follows:

$$P=-\frac{2\text{sin}(w\cdot (t_d-t_s))\times S\text{max}}{\sqrt{2w}{T}_0}$$

(12)

If the time series of the surface temperature and NSSR can be derived (more than six observations), three parameters (S_max, t_s and w) in Equation (6) and two parameters (T₀ and t_d) in Equation (8) can be estimated by fitting Equations (6) and (8) using least square method, then P can be obtained using w × (t_d − t_s), T₀ and S_max with Equation (12).

Thermal inertia represents the resistance to a temperature change in the upper few centimeters of the surface throughout the day, and it is independent of the local time, latitude, and season. A higher thermal inertia corresponds to a slower change in the temperature for the same incoming energy [13]. Solar radiation is the primary type of energy that reaches the Earth’s surface; thus, the surface temperature decreases when the sky is overcast. Because of the character of thermal inertia, the change in temperature lags behind the reduced incoming solar radiation. For example, the time at which the temperature is maximized (t_d) often lags behind the time at which the NSSR is maximized (t_s). Meanwhile, the amplitude of the variation in surface temperature is also affected by thermal inertia. When the sky is cloudy, the reduced incoming solar radiation causes a drop in the LST; but, the time in temperature change will be postponed, perhaps lasts t_d − t_s, and the amplitude of the temperature change increases incrementally (from 0 to 1). Assuming that the LST variations are caused by variations in insolation (ΔS), which is related to cloudiness, at the same time, the amplitudes of the LST variations are related to thermal inertia (P). Considering ΔS is less than 500 W∙m⁻², and P changes from 400 to 4000 W∙s^1/2∙m⁻²∙k⁻¹ in most situations, Lu et al. [8] also pointed out the ratio of solar radiation change and temperature change is between 30 and 300. So, the amplitudes of the LSTs variations are enlarged by a factor of 10. The method to calculate the daytime LST under cloudy skies combining the diurnal solar radiation and surface temperature is proposed as follows:

T_cloud = T_clear – 10 × ΔS/P

(13)

where T_cloud is the LST under cloudy skies, T_clear is the LST under cloud-free skies (estimated using Equation (8)), and ΔS is the difference in the NSSR values between clear or cloudy skies. Considering the lag between LST variations and insolation variations, ΔS cannot attain a maximum once a cloud appears. Instead, the value reaches a maximum at some time after a cloud appears (t_d − t_s). Moreover, the degree of the influence increases incrementally (from 0–1). Therefore, ΔS is given as follows:

$$\Delta S={\displaystyle \sum _{t=t_{now}-(td-ts)}^{t_{now}}(S_{fit}(t)-S_{actual}(t))\times \text{cos}[w\times (t-t_{now}})]\times \frac{t_d-t_s-(t-t_{now})}{t_d-t_s}$$

(14)

where S_actual is the actual NSSR at t time, S_fit is fitted using Equation (6) which means NSSR under cloud-free skies (NSSR_clear) at t time, and t is time.

To sum up, if the time series of the surface temperature and NSSR can be derived (more than six observations), three parameters (S_max, t_s and w) in Equation (6) and two parameters (T₀ and t_d) in Equation (8) can be estimated by fitting Equations (6) and (8) using least square method, then P can be obtained using w × (t_d − t_s), T₀ and S_max with Equation (12). Meanwhile, T_clear at any time during the daytime can be estimated using Equation (8) with six parameters (T, T₀, w, t_d, t_s, and β which are inversed using more than six observations with least square method). Similarly, NSSR_clear can be also obtained using Equation (6), and ΔS can be calculated after NSSR_clear minus observed NSSR, in the end, substituting these variables (T_clear, ΔS and P) to Equation (13), T_cloud can be calculated.

Notably, the method of estimating thermal inertia is based on homogeneous bare soil, which is not realistic. So, the P in Equations (12) and (13) is defined as the apparent thermal inertia. Furthermore, in the process of inducing thermal inertia, the angular diurnal frequency (w) is the same for Equations (6) and (8). Considering the varying atmospheric conditions and underlying surfaces, w exhibits a slight difference. Therefore, the mean w (for NSSR and LST) is used to obtain the LST under cloudy skies. Figure 1 presents a flow chart for estimating LST under cloudy skies.

3. Data

3.1. Data from Field Experiments

To validate the proposed method, in situ data were collected from the Chang Wu experimental station located in Shaanxi Province (107°40′E and 35°12′N), which joined the Chinese Ecosystem Research Network in 1991. The site comprises a field dominated by wheat and corn in the proximity of the meteorological station. Incoming and reflected solar radiation were measured by a pyranometer. Non-contact infrared thermometers were used to measure the surface temperature. Data for an entire year (i.e., 2012) collected at 1-h intervals were used for validation in this study.

3.2. Satellite Data

The 12 spectral channels of MSG/SEVIRI cover a range of visible, near-infrared and thermal-infrared bands. The LST under cloud-free skies can be obtained from the atmospheric windows of 3.9, 8.7, 10.8 and 12.0 µm [14,15,16]. The NSSR can be estimated from the visible and near-infrared channels (0.6, 0.8, 1.6, and 3.9 µm) [17,18]. In this study, the LST, Down-welling Surface Short-wave Radiation Flux (DSSF) and surface albedo products for 1 April 2012, were downloaded from the Land Surface Analysis Satellite Applications Facility [19] to determine the LST under cloudy skies.

Figure 1. Flow chart of estimated LST under cloudy skies.

Figure 1. Flow chart of estimated LST under cloudy skies.

4. Results and Discussions

4.1. LST under a Cloudy Sky

Field measurements collected from the Chang Wu experimental station are used to validate the proposed method; the results are discussed below.

4.1.1. Determining Parameters in the DTC Model

As discussed by Duan et al. [20,21,22], the DTC model can only be used to describe the LST diurnal cycle under cloud-free skies, i.e., the LST estimated using Equation (8) denotes the LST under cloud-free conditions. If the sky is overcast, the LST daily evolution cannot be determined using the DTC model. Considering that the LST is the same as that under cloud-free skies before a cloud appears or sometime after a cloud disappears, we believe the DTC model parameters can be estimated using observations from cloud-free conditions. Moreover, under overcast skies, the LST is lower than the LST under clear skies [6]. Therefore, some prior information can be assumed: (1) the fitted LST is equal to or slightly higher than the actual LST when inverting the six parameters; (2) the observations collected before a cloud first appears or at some time (assumed to be 2 h in this study) after a cloud disappears are given higher weights (set to 2) when inverting the six parameters, while observations under cloud-free skies are given lower weights (set to 1). In general, the six parameters can be estimated using more than six T_clear observations. However, the six T_clear observations must be distributed throughout the day, i.e., they cannot be concentrated in the morning or afternoon. Figure 2 displays the fitted results for six days under various cloud conditions. The black points denote the measured LST under cloud-free skies, and the black hollow points denote the LST fitted using Equation (8). The root-mean-square error (RMSE) between the measured LST and the predicted LST using Equation (8) are within 2 K. The fit is suitable for the daytime but not for the nighttime. Although the overcast time is different among the six days, the DTC model can be used to describe the daily LST evolution, even when most of the daytime is cloudy (e.g., 8 June in Figure 2).

Figure 2. Comparison of the measured daily temperature evolution with that predicted by the DTC model for six days under various cloud conditions.

Figure 2. Comparison of the measured daily temperature evolution with that predicted by the DTC model for six days under various cloud conditions.

4.1.2. Determining the Parameters in the DSC Model

Prior knowledge that the fitted NSSR is equal to or slightly higher than the actual NSSR is considered when inverting the four parameters in Equation (6) [23]. Four parameters can be obtained from more than four NSSR observations using Equation (6). Like the LST, the four observations cannot be concentrated in the morning or afternoon; the observations must be distributed throughout the day. The diurnal NSSR cycle is shown in Figure 3, which delineates the DSC curve for six days under various cloud cover conditions. The red hollow points denote the measured NSSR in one day, and the black points denote the NSSR fitted using Equation (6), i.e., the clear-sky NSSR (NSSR_clear). Considering that clouds suppress the amount of solar radiation reaching the surface, it is assumed that the fitted NSSR is equal to or slightly higher than the actual NSSR. Therefore, the RMSEs between the measured and predicted NSSR are large; most RMSEs exceed 170 W∙m⁻². However, the fitted curve reflects the changes in the NSSR in one day and suggests that the DSC model described in Equation (6) can predict the diurnal NSSR evolution on clear days. Just as shown in Figure 2 and Figure 3, measured diurnal LST curve is smoother than measured diurnal NSSR curve, it is because LST will display the slow process of change and the time in LST change lag the time in the reduced incoming solar radiation under the influence of thermal inertia.

Figure 3. Comparison of the measured daily NSSR evolution with that predicted by the DSC model for six days under various cloud cover conditions.

Figure 3. Comparison of the measured daily NSSR evolution with that predicted by the DSC model for six days under various cloud cover conditions.

4.1.3. Estimation of LST Under a Cloudy Sky

T_cloud is calculated by the proposed method after obtaining T_clear, NSSR_clear and thermal inertia using Equations (6), (8) and (13), and the results for the six days are shown in Figure 4. The black points denote the measured LST under cloud-free skies, the red solid points denote the measured LST under cloudy skies, and the red hollow points denote the estimated LST using the proposed method. The RMSE values of the measured and estimated LST are 1.2, 1.8, 1.05, 1.2, 0.8 and 0.72 K for April 17, June 8, June 15, June 22, August 21 and September 28, respectively. Compared with the other five days, the overcast time on 8 June was much longer, which influenced the fit (Equation (8)) shown in Figure 2. As a result, the absolute errors of the measured LST and the predicted LST using Equation (13) on 8 June are higher than those on the other five days. Compared to the RMSEs between the measured and estimated LSTs under cloud-free conditions (Figure 2), the RMSE between the measured and estimated LSTs is smaller on 28 September. Because errors between the measured and estimated LSTs under cloud-free conditions are primarily produced at night (after midnight) and the RMSE between the measured and estimated daytime LSTs under cloud-free conditions is only 1.10 K, the RMSE is smaller on 28 September. The curve of the LST predicted by Equation (13) is very similar to that of the measured LST under cloudy skies on 17 April, 15 June, 22 June, 21 August and 28 September; therefore, Equation (13) can be used to describe the response of the LST changes to variations in the NSSR. Prior knowledge that the fitted LST is equal to or slightly higher than the actual LST when estimating the six parameters in Equation (8) suggests that a few of the measured LSTs under cloud-free skies are less than the estimated LSTs.

Figure 4. Comparison of the measured daily temperature evolution with that predicted by the proposed method for six days under various cloud conditions.

Figure 4. Comparison of the measured daily temperature evolution with that predicted by the proposed method for six days under various cloud conditions.

Figure 5 shows a comparison of the measured daytime LST and the estimated daytime LST using the proposed method under cloudy skies at the Chang Wu Ecosystem experimental station in 2012 (excluding the days in which less than six T_clear observations are available). The scatter plot shows that most points are distributed near the 1:1 line, and the RMSE is 1.23 K. The histogram indicates that most errors between the measured LST and the estimated LST using the proposed method under cloudy skies are distributed within ±2 K. The maximum error is −6 K, implying that the proposed method can be used to estimate the LST under cloudy skies by combining the diurnal solar radiation with surface temperature under clear skies. The errors are caused by the uncertainty in the algorithm, DTC, the DSC model, and measurement errors, among other factors.

Figure 5. Comparison of the measured daytime LST and the daytime LST predicted by the proposed method under cloudy skies at the Chang Wu Ecosystem experimental station in 2012 (left: scatter plot; right: histogram of errors of the measured and estimated LST).

Figure 5. Comparison of the measured daytime LST and the daytime LST predicted by the proposed method under cloudy skies at the Chang Wu Ecosystem experimental station in 2012 (left: scatter plot; right: histogram of errors of the measured and estimated LST).

4.2. Error Analysis

4.2.1. Sensitivity to Errors of the Estimated LST Under Cloud-Free Skies

The LST under cloudy skies (T_cloud) is retrieved using T_clear observations in the proposed method. In general, T_clear is obtained using infra-thermal band data, and errors are unavoidable due to the uncertainty in the emissivity, unknown atmospheric conditions and the inversed method, etc. Thus, errors in T_clear are fully translated into errors in the estimation of T_cloud. Regarding the errors in T_cloud from T_clear, a sensitivity analysis is performed by adding ±0.25 K and ±0.5 K to the actual T_clear. Figure 6 shows the resulting error histograms. The RMSE values of the measured and estimated T_cloud are 1.34, 1.39, 1.36 and 1.44 K with a mean error of 0.35 K, 0.12 K, −0.57 K and −0.34 K, respectively when adding −0.25, −0.5, 0.25 and 0.5 K biases to the real T_clear. We find that most errors in T_cloud are within ±2.5 K from the histogram of errors. The mean error is positive when T_clear is underestimated, while the mean error is negative when T_clear is overestimated.

4.2.2. Sensitivity to Errors in the Estimated NSSR

In the algorithm, the daily NSSR evolution is needed. The NSSR values estimated by the method will produce some errors, and the errors will be translated into errors in the estimation of T_cloud. Regarding the errors in T_cloud introduced by NSSR, a sensitivity analysis is performed after adding ±5 and ±10 percent NSSR biases to the actual NSSR, respectively. Figure 7 shows the corresponding histograms of errors. The RMSE values of the measured and estimated T_cloud are 1.484, 1.424, 1.42 and 1.31 K with a mean error of −0.05 K, −0.05 K, −0.13 K and −0.14 K respectively after adding −5, −10, 5 and 10 percent NSSR biases to the actual NSSR.

Figure 6. Histogram of errors in the measured T_cloud and in the estimated T_cloud based on adding biases to T_clear ((A): add a −0.25 K bias; (B): add a −0.5 K bias; (C): add a 0.25 K bias; and (D): add a 0. 5 K bias).

Figure 6. Histogram of errors in the measured T_cloud and in the estimated T_cloud based on adding biases to T_clear ((A): add a −0.25 K bias; (B): add a −0.5 K bias; (C): add a 0.25 K bias; and (D): add a 0. 5 K bias).

Figure 7. Histogram of errors of the measured T_cloud and the estimated T_cloud after adding biases to the NSSR ((A): add a −5 percent NSSR bias to the actual NSSR; (B): add a −10 percent NSSR bias to the actual NSSR; (C): add a 5 percent NSSR bias to the actual NSSR; and (D): add a 10 percent NSSR bias to the actual NSSR).

Figure 7. Histogram of errors of the measured T_cloud and the estimated T_cloud after adding biases to the NSSR ((A): add a −5 percent NSSR bias to the actual NSSR; (B): add a −10 percent NSSR bias to the actual NSSR; (C): add a 5 percent NSSR bias to the actual NSSR; and (D): add a 10 percent NSSR bias to the actual NSSR).

5. Application to Actual MSG-SEVIRI Satellite Data

The objective of the present work is to estimate the LST under cloudy skies from MSG data. Figure 8 provides an example of the LST retrieval using geospatial coverage between 35°N–50°N and 20°E–30°E during the MSG scan on 1 April 2012 at 11:00 UTC. Figure 8 (right) is the LST product from the Land Surface Analysis Satellite Applications Facility (LSASAF), and the black region in the middle of the picture denotes invalid values due to the cloud cover. The black regions are filled with the LST predicted by the proposed method (Figure 8, left).

Figure 8. Comparison of LST products from LSASAF, with the LST estimated by the proposed method on 1 April 2012 at 11:00 UTC (left: estimates from the proposed method; right: the LST products).

Figure 8. Comparison of LST products from LSASAF, with the LST estimated by the proposed method on 1 April 2012 at 11:00 UTC (left: estimates from the proposed method; right: the LST products).

The LSTs under cloudy skies are not validated due to the lack of in situ measurements and remotely sensed data from other sources. Validation of LSTs at the satellite pixel scale is challenging because LSTs can vary significantly within a pixel and change within relatively short time periods [21]. However, the LSTs are generally similar to neighboring pixels. Due to the appearance of clouds, LSTs under cloudy skies are lower than that under cloud-free skies. Figure 8 presents the results from 44°–45°N and 28°–29°E, which means that the method can be used to estimate LSTs under cloudy skies. Considering the absent of LST product under cloudy conditions, comparison of LST product from LSASAF and LST estimated using proposed method under cloud-free skies is performed and the RMSE is 1.3 K with a mean error of −0.5 K.

6. Conclusions

With more and more geostationary meteorological satellites in operation, the estimation of LST for cloudy pixels is required. In this paper, we proposed a new method to estimate LST under cloudy skies by combining diurnal solar radiation with surface temperatures.

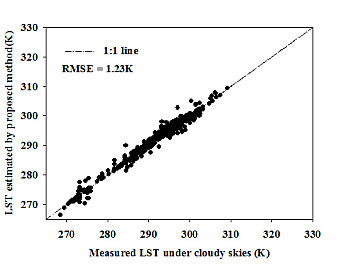
The RMSE between the in situ LST from the Chang Wu experimental station located in Shaanxi Province (107°40′E and 35°12′N) and the predicted value is 1.23 K; thus, the proposed algorithm can be used to calculate LST under cloudy skies.

The proposed method requires the use of LST under cloud-free skies (T_clear) and diurnal NSSR. Considering the errors in the estimated LST under cloudy conditions (T_cloud) when using NSSR and T_clear, a sensitivity analysis regarding the uncertainty of T_clear and NSSR was also performed. The results show that the accuracy of the LST retrieval can be off by 0.11 K, 0.16 K, 0.17 K and 0.21 K, respectively, when adding a −0.25 K, −0.5 K, 0.25 K and 0.5 K bias to the actual T_clear. The effect of the uncertainty in the NSSR on the LST retrieval could be approximately 0.254, 0.194, 0.19 and 0.08 K, respectively, when adding −5, −10, 5 and 10 percent NSSR errors to the real NSSR.

Finally, T_cloud was calculated using T_clear and Down-welling Surface Short-wave Radiation Flux (DSSR) and albedo products of MSG2-SEVIRI from the Land Surface Analysis Satellite Applications Facility (LSASAF) using the new method. The new algorithm can be applied to LST data retrieved from a geo-stationary satellite during cloudy conditions, and it provides the ability to reconstruct diurnal LST cycles from geo-stationary satellite observations. These cycles are particularly useful in regions where ground-based meteorological observations are scarce.

Notably, the proposed method assumes that the variation in the LST is caused by variations in insolation (which is related to cloudiness) during the daytime. Therefore, the approach can only be used during the daytime. Furthermore, at least six T_clear values in one day are needed to fit the DTC model; therefore, the algorithm cannot be used to estimate the LST when less than six T_clear observations are available. These limitations will be addressed in future research.