Ocean Wave Parameters Retrieval from TerraSAR-X Images Validated against Buoy Measurements and Model Results
Abstract
:1. Introduction
2. Satellite and Buoy Data
| Time (UTC) | Swath (Km) | Incidence Angle (°) | Range×Azimuth Resolution (m) | Center Location(°W, °N) |
|---|---|---|---|---|
| 6 February 2008 02:00 | 5 × 3 | 29.6–32.6 | 1.25 × 1.25 | 122.5, 37.2 |
| 22 February 2008 02:08 | 5 × 3 | 41.6–44.0 | 1.25 × 1.25 | 123,2, 38.1 |
| 3 December 2008 05:39 | 8 × 10 | 22.3–32.5 | 8.25 × 8.25 | 179.3, 51.3 |
| 29 January 2009 23:56 | 8 × 10 | 22.3–34.9 | 8.25 × 8.25 | 90.3, 25.8 |
| 22 July 2009 17:03 | 5 × 3 | 34.0–36.7 | 1.25 × 1.25 | 160.6, 54.3 |
| 12 August 2009 04:14 | 5 × 3 | 31.8–34.6 | 1.25 × 1.25 | 153.9, 22.9 |
| 5 December 2010 22:50 | 15 × 10 | 22.3–32.7 | 8.25 × 8.25 | 75.1, 35.5 |
| 13 December 2010 16:19 | 15 × 10 | 22.3–32.5 | 8.25 × 8.25 | 154.1, 23.4 |
| 24 December 2010 16:19 | 15 × 10 | 19.7–30.3 | 8.25 × 8.25 | 153.8, 23.5 |
| 13 March 2011 14:07 | 15 × 10 | 37.9–45.6 | 8.25 × 8.25 | 121.1, 35.2 |
| 29 October 2011 15:54 | 5 × 3 | 31.8–34.6 | 1.25 × 1.25 | 142.4, 55.8 |
| 5 November 2011 02:30 | 5 × 3 | 24.9–28.1 | 1.25 × 1.25 | 122.4, 37.2 |
| 23 January 2012 22:20 | 5 × 3 | 31.7–34.6 | 1.25 × 1.25 | 64.9, 21.1 |
| 25 January 2012 21:51 | 5 × 3 | 22.3–25.6 | 1.25 × 1.25 | 62.1, 42.2 |
| 29 January 2012 10:03 | 5 × 3 | 34.0–36.7 | 1.25 × 1.25 | 58.0, 43.0 |
| 5 February 2012 02:56 | 5 × 3 | 36.0–38.6 | 1.25 × 1.25 | 138.8, 53.9 |
| Geographic Coordinate (°W, °N) | Time (UTC) | in situ | SAR-derived | ||||
|---|---|---|---|---|---|---|---|
| WDIR | WSPD | SWH | MWP | WDIR | WSPD | ||
| 122.8, 37.7 | 6 February 2008 | 330 | 7.9 | 2.28 | 7.48 | 317 | 6.4 |
| 123.3, 38.2 | 22 February 2008 | 283 | 5.9 | 3.39 | 7.40 | 274 | 4.8 |
| 89.7, 25.9 | 29 January 2009 | 29 | 10.1 | 1.46 | 5.13 | 33 | 8.2 |
| 75.4, 35.0 | 5 December 2010 | 313 | 11.4 | 1.90 | 4.82 | 303 | 13.5 |
| 153.9, 23.6 | 13 December 2010 | 134 | 6.7 | 1.85 | 5.62 | 137 | 4.8 |
| 153.9, 23.6 | 24 December 2010 | 182 | 5.0 | 1.76 | 6.43 | 206 | 4.3 |
| 120.9, 35.0 | 13 March 2011 | 330 | 4.5 | 2.13 | 8.86 | 350 | 3.4 |
| 142.5, 55.9 | 20 October 2011 | 241 | 12.1 | 3.26 | 6.12 | 240 | 9.5 |
| 64.9, 21.1 | 23 January 2012 | 78 | 8.2 | 1.76 | 5.10 | 63 | 7.4 |

3. SAR Wave Parameter Retrieval Methodology
3.1. Empirical Wave Model
3.2. SAR Wind Retrieval
3.3. Scheme of Wave Retrieval Algorithm: PFSM

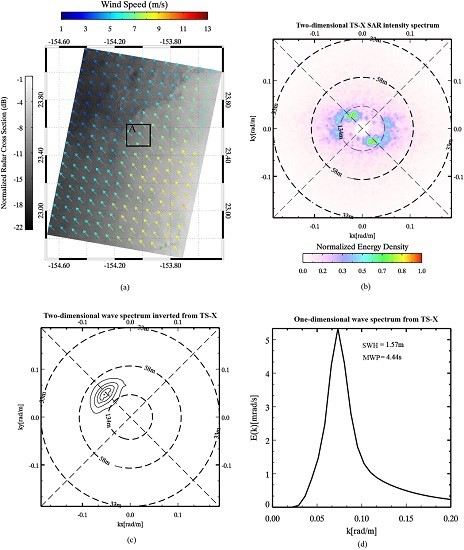
4. SAR Wave Retrieval Validation


| SWH(m) SAR-Derived | MWP(s) SAR-Derived | SWH(m) in situ | MWP(s) in situ | SWH(m) WAVEWATCH-III | MWP(s) WAVEWATCH-III |
|---|---|---|---|---|---|
| 1.57 | 4.44 | 1.82 | 5.62 | 2.15 | 6.8 |
| Bias | −0.25 | −1.18 | −0.58 | −2.36 | |

5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, X.M.; Lehner, S. Algorithm for sea surface wind retrieval from TerraSAR-X and TanDEM-X Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2928–2939. [Google Scholar]
- Ren, Y.Z.; He, M.X.; Lehner, S. An algorithm for the retrieval of sea surface wind fields using X-band TerraSAR-X data. Int. J. Remote Sens. 2012, 33, 7310–7336. [Google Scholar] [CrossRef]
- Shao, W.Z.; Li, X.M.; Lehner, S.; Guan, C.L. Development of Polarization Ratio model for sea surface wind field retrieval from TerraSAR-X HH polarization data. Int. J. Remote Sens. 2014, 35, 4046–4063. [Google Scholar] [CrossRef]
- Alpers, W.; Ross, D.B.; Rufenach, C.L. On the detectability of ocean surface waves by real and synthetic radar. J. Geophys. Res. 1981, 86, 10529–10546. [Google Scholar] [CrossRef]
- Hasselmann, S.; Hasselmann, K. Computations and parametrizations of the nonlinear energy transfer in a gravity-wave spectrum. I: A new method for efficient computations of the exact nonlinear transfer integral. J. Phys. Oceanogr. 1985, 15, 1369–1377. [Google Scholar] [CrossRef]
- Alpers, W.; Bruning, C. On the relative importance of motion-related contributions to SAR imaging mechanism of ocean surface waves. IEEE Trans. Geosci. Remote Sens. 1986, 24, 873–885. [Google Scholar] [CrossRef]
- Li, X.F.; Pichel, W.; He, M.; Wu, S.; Friedman, K.; Clemente-Colon, P.; Zhao, C. Observation of hurricane-generated ocean swell refraction at the Gulf Stream North Wall with the RADARSAT-1 synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2131–2142. [Google Scholar]
- Hasselmann, K.; Hasselmann, S. On the nonlinear mapping of an ocean wave spectrum into a synthetic aperture radar image spectrum. J. Geophys. Res. 1991, 96, 10713–10729. [Google Scholar] [CrossRef]
- Hasselmann, S.; Bruning, C.; Hasselmann, K. An improved algorithm for the retrieval of ocean wave spectra from synthetic aperture radar image spectra. J. Geophys. Res. 1996, 101, 6615–6629. [Google Scholar] [CrossRef]
- Schulz-Stellenfleth, J.; Lehner, S.; Hoja, D. A parametric scheme for the retrieval of two-dimensional ocean wave spectra from synthetic aperture radar look cross spectra. J. Geophys. Res. 2005, 110, 97–314. [Google Scholar] [CrossRef]
- Mastenbroek, C.; de Valk, C.F. A semi-parametric algorithm to retrieve ocean wave spectra from synthetic aperture radar. J. Geophys. Res. 2000, 105, 3497–3516. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of Wind-Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP); UDC 551.466.31; Deutches Hydrographisches Institut: Hamburg, Germany, 1973. [Google Scholar]
- Voorrips, C.; Makin, V.; Hasselmann, S. Assimilation of wave spectra from pitch-and-roll buoys in a North Sea wave model. J. Geophys. Res. 1997, 102, 5829–5849. [Google Scholar] [CrossRef]
- Sun, J.; Guan, C.L. Parameterized first-guess spectrum method for retrieving directional spectrum of swell-dominated waves and huge waves from SAR images. Chin. J. Oceanol. Limnol. 2006, 24, 12–20. [Google Scholar]
- Sun, J.; Kawamura, H. Retrieval of surface wave parameters from SAR images and their validation in the coastal seas around Japan. J. Oceanogr. 2009, 65, 567–577. [Google Scholar] [CrossRef]
- Schulz-Stellenfleth, J.; Konig, T.; Lehner, S. An empirical approach for the retrieval of integral ocean wave parameters from synthetic aperture radar data. J. Geophys. Res. 2007, 112, 1–14. [Google Scholar]
- Li, X.M.; Lehner, S.; Rosenthal, W. Investigation of ocean surface wave refraction using TerraSAR-X data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 830–840. [Google Scholar]
- Li, X.M.; Lehner, S.; Bruns, T. Ocean wave integral parameter measurements using Envisat ASAR wave mode data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 155–174. [Google Scholar] [CrossRef]
- Bruck, M.; Lehner, S. Coastal wave field extraction using TerraSAR-X data. J. Appl. Remote Sens. 2013. [Google Scholar] [CrossRef]
- Yang, X.F.; Li, X.F.; Pichel, W.; Li, Z.W. Comparison of ocean surface winds from ENVISAT ASAR, MetOp ASCAT scatterometer, buoy measurements, and NOGAPS model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4743–4750. [Google Scholar] [CrossRef]
- Wackerman, C.; Clemente-Colon, P.; Pichel, W.; Li, X. A two-scale model to predict C-band VV and HH normalized radar cross section values over the ocean. Can. J. Remote Sens. 2002, 28, 367–384. [Google Scholar]
- Yang, X.; Li, X.; Zheng, Q.; Gu, X.; Pichel, W.; Li, Z.W. Comparison of ocean-surface winds retrieved from QuikSCAT scatterometer and Radarsat-1 SAR in offshore waters of the U.S. west coast. IEEE Geosci. Remote Sens. Lett. 2011, 8, 163–167. [Google Scholar] [CrossRef]
- Xu, Q.; Lin, H.; Li, X.F.; Zheng, Q.; Pichel, W.; Liu, Y. Assessment of an analytical model for sea surface wind speed retrieval from spaceborne SAR. Int. J. Remote Sens. 2010, 31, 993–1008. [Google Scholar]
- Zhang, B.; Li, X.; Perrie, W.; He, Y. Synergistic measurements of ocean winds and waves from SAR. J. Geophys. Res. 2015. [Google Scholar] [CrossRef]
- Tolman, H.L. A mosaic approach to wind wave modeling. Ocean Model. 2008, 25, 35–47. [Google Scholar] [CrossRef]
- Alpers, W.; Rufenach, C. The effect of orbital motions on synthetic aperture radar imagery of ocean waves. IEEE Trans. Antenn. Propag. 1979, 27, 685–690. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, J.; Yang, J. A semiempirical algorithm for SAR wave height retrieval and its validation using Envisat ASAR wave mode data. Acta Oceanol. Sin. 2012, 31, 59–66. [Google Scholar] [CrossRef]
- Monaldo, F.M.; Beal, R.C. Comparison of SIR-C SAR wavenumber spectra with WAM model predictions. J. Geophys. Res. 1998, 103, 18815–18825. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Hauser, D.; Caudal, G.; Chapron, B. A semiempirical model of the normalized radar cross section of the sea surface, 2. Radar modulation transfer function. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Phillips, O.M.; Posner, F.L.; Hansen, J.P. High range resolution radar measurements of the speed distribution of breaking events in wind-generated ocean waves: Surface impulse and wave energy dissipation rates. J. Phys. Oceanogr. 2001, 31, 450–460. [Google Scholar] [CrossRef]
- Haller, M.C.; Lyzenga, D.R. Comparison of radar and video observations of shallow water breaking waves. IEEE Geosci. Remote Sens. Lett. 2003, 41, 832–844. [Google Scholar] [CrossRef]
- Cavaleri, L. Wave modeling—Missing the peaks. J. Phys. Oceanogr. 2009, 39, 2757–2778. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, W.; Li, X.; Sun, J. Ocean Wave Parameters Retrieval from TerraSAR-X Images Validated against Buoy Measurements and Model Results. Remote Sens. 2015, 7, 12815-12828. https://doi.org/10.3390/rs71012815
Shao W, Li X, Sun J. Ocean Wave Parameters Retrieval from TerraSAR-X Images Validated against Buoy Measurements and Model Results. Remote Sensing. 2015; 7(10):12815-12828. https://doi.org/10.3390/rs71012815
Chicago/Turabian StyleShao, Weizeng, Xiaofeng Li, and Jian Sun. 2015. "Ocean Wave Parameters Retrieval from TerraSAR-X Images Validated against Buoy Measurements and Model Results" Remote Sensing 7, no. 10: 12815-12828. https://doi.org/10.3390/rs71012815
APA StyleShao, W., Li, X., & Sun, J. (2015). Ocean Wave Parameters Retrieval from TerraSAR-X Images Validated against Buoy Measurements and Model Results. Remote Sensing, 7(10), 12815-12828. https://doi.org/10.3390/rs71012815