Assessing Optimal Flight Parameters for Generating Accurate Multispectral Orthomosaicks by UAV to Support Site-Specific Crop Management
Abstract
:1. Introduction
2. Material and Methods
2.1. UAV and Sensor Description

2.2. Study Site and UAV Flights
2.3. Photogrammetric Processing
2.4. Assessment of Spatial Resolution

2.5. Assessment of Spectral Discrimination

3. Results
| Flight Duration | Wind Speed (m/s) | ||||
|---|---|---|---|---|---|
| AGL (m) | Route Length (m) | Stop Mode | Cruising Mode | Stop Mode | Cruising Mode |
| 60 | 10,740 | 38 min 11 s | 9 min 28 s | 0.8 | 1.3 |
| 80 | 8045 | 18 min 24 s | 4 min 46 s | 1.3 | 1.8 |
| 100 | 9254 | 11 min 56 s | 3 min 40 s | 1.8 | 1.9 |

3.1. Effect of UAV Flights Parameters on Orthophoto Spatial Resolution
| AGL (m) | Flight Mode | 4 GCPs RMSE (cm) | 5 GCPs RMSE (cm) | ||
|---|---|---|---|---|---|
| FA | SM | FA | SM | ||
| 60 | Stop | 14.7 | 11.6 | 14.5 | 11.7 |
| Cruising | 9.8 | 5.1 | 8.3 | 5.3 | |
| 80 | Stop | 16.6 | 14.7 | 16.4 | 14. 3 |
| Cruising | 13.1 | 9.3 | 8.5 | 6.3 | |
| 100 | Stop | 28.8 | 18.2 | 23.2 | 16.5 |
| Cruising | 13.5 | 12.1 | 9.7 | 9.2 | |


| AGL (m) | Flight Mode | 4 GCPs RMSE (cm) | 5 GCPs RMSE (cm) |
|---|---|---|---|
| 60 | Stop | 19.5 | 18.5 |
| Cruising | 14.5 | 11.3 | |
| 80 | Stop | 21.0 | 10.8 |
| Cruising | 11.0 | 9.5 | |
| 100 | Stop | 22.7 | 14.9 |
| Cruising | 14.8 | 13.5 |
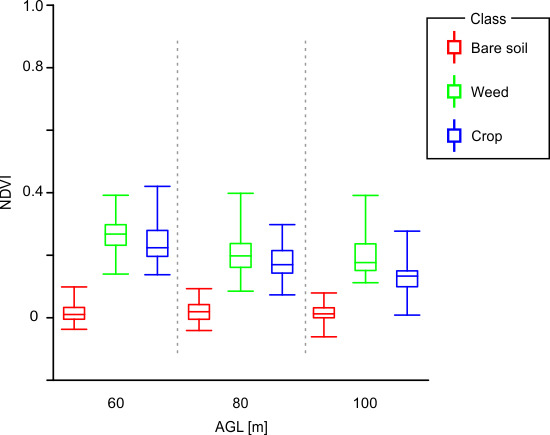
3.2. Effect of UAV Flights Parameters on Orthophoto Spectral Discrimination

| NDVI | 60 m AGL | 80 m AGL | 100 m AGL | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Statistics | V | W | C | B | V | W | C | B | V | W | C | B |
| Minimum | 0.14 | 0.14 | 0.13 | −0.03 | 0.07 | 0.08 | 0.07 | −0.04 | 0.01 | 0.11 | 0.01 | −0.03 |
| Maximum | 0.42 | 0.39 | 0.42 | 0.09 | 0.40 | 0.39 | 0.29 | 0.09 | 0.39 | 0.39 | 0.27 | 0.07 |
| Deviation | 0.06 | 0.05 | 0.06 | 0.02 | 0.06 | 0.07 | 0.05 | 0.02 | 0.07 | 0.06 | 0.05 | 0.02 |
| Mean | 0.25 | 0.26 | 0.24 | 0.01 | 0.20 | 0.21 | 0.18 | 0.02 | 0.17 | 0.19 | 0.13 | 0.01 |
| Median | 0.25 | 0.26 | 0.22 | 0.01 | 0.19 | 0.19 | 0.17 | 0.01 | 0.02 | 0.17 | 0.13 | 0.01 |
| Classes | 60 m | 80 m | 100 m | |||
|---|---|---|---|---|---|---|
| Crop | Bare Soil | Crop | Bare Soil | Crop | Bare Soil | |
| Weed | 0.23 | 3.06 | 0.24 | 1.88 | 0.52 | 1.92 |
| Crop | - | 2.51 | - | 1.94 | - | 1.38 |
| Vegetation | - | 2.74 | - | 1.86 | - | 1.55 |

4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Srbinovska, M.; Gavrovski, C.; Dimcev, V.; Krkoleva, A.; Borozan, V. Environmental parameters monitoring in precision agriculture using wireless sensor networks. J. Clean. Prod. 2015, 88, 297–307. [Google Scholar] [CrossRef]
- Mulla, D.J. Twenty five years of remote sensing in precision agriculture: Key advances and remaining knowledge gaps. Biosyst. Eng. 2013, 114, 358–371. [Google Scholar] [CrossRef]
- Ge, Y.; Thomasson, J.A.; Sui, R. Remote sensing of soil properties in precision agriculture: A review. Front. Earth Sci. 2011, 5, 229–238. [Google Scholar] [CrossRef]
- De Castro, A.; López-Granados, F.; Jurado-Expósito, M. Broad-scale cruciferous weed patch classification in winter wheat using QuickBird imagery for in-season site-specific control. Precis. Agric. 2013, 14, 392–413. [Google Scholar] [CrossRef]
- López-Granados, F.; Jurado-Expósito, M.; Peña-Barragán, J.M.; García-Torres, L. Using geostatistical and remote sensing approaches for mapping soil properties. Eur. J. Agron. 2005, 23, 279–289. [Google Scholar] [CrossRef]
- Abbas, A.; Khan, S.; Hussain, N.; Hanjra, M.A.; Akbar, S. Characterizing soil salinity in irrigated agriculture using a remote sensing approach. Phys. Chem. Earth 2013, 55–57, 43–52. [Google Scholar] [CrossRef]
- Laliberte, A.S.; Goforth, M.A.; Steele, C.M.; Rango, A. Multispectral remote sensing from unmanned aircraft: Image processing workflows and applications for rangeland environments. Remote Sens. 2011, 3, 2529–2551. [Google Scholar] [CrossRef]
- López-Granados, F. Weed detection for site-specific weed management: Mapping and real-time approaches. Weed Res. 2011, 51, 1–11. [Google Scholar] [CrossRef]
- Zhang, C.; Kovacs, J. The application of small unmanned aerial systems for precision agriculture: A review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Rango, A.; Laliberte, A.; Steele, C.; Herrick, J.E.; Bestelmeyer, B.; Schmugge, T.; Roanhorse, A.; Jenkins, V. Using unmanned aerial vehicles for rangelands: Current applications and future potentials. Environ. Pract. 2006, 8, 159–168. [Google Scholar] [CrossRef]
- Peña, J.M.; Torres-Sánchez, J.; de Castro, A.I.; Kelly, M.; López-Granados, F. Weed mapping in early-season maize fields using object-based analysis of unmanned aerial vehicle (UAV) images. PLoS ONE 2013, 8, e77151. [Google Scholar]
- Paparoditis, N.; Souchon, J.-P.; Martinoty, G.; Pierrot-Deseilligny, M. High-end aerial digital cameras and their impact on the automation and quality of the production workflow. ISPRS J. Photogramm. Remote Sens. 2006, 60, 400–412. [Google Scholar] [CrossRef]
- Markelin, L.; Honkavaara, E.; Hakala, T.; Suomalainen, J.; Peltoniemi, J. Radiometric stability assessment of an airborne photogrammetric sensor in a test field. ISPRS J. Photogramm. Remote Sens. 2010, 65, 409–421. [Google Scholar] [CrossRef]
- Ackermann, F. Operational Rules and Accuracy Models for GPS-Aerotriangulation. Available online: http://www.isprs.org/proceedings/xxix/congress/part3/691_XXIX-part3.pdf (accessed on 17 June 2015).
- Müller, J.; Gärtner-Roer, I.; Thee, P.; Ginzler, C. Accuracy assessment of airborne photogrammetrically derived high-resolution digital elevation models in a high mountain environment. ISPRS J. Photogramm. Remote Sens. 2014, 98, 58–69. [Google Scholar] [CrossRef]
- European Commission Joint Research Centre. Inspire Data Specification for the Spatial Data Theme Orthoimagery. Available online: http://inspire.ec.europa.eu/index.cfm/pageid/2 (accessed on 17 June 2015).
- Zhang, Y.; Xiong, J.; Hao, L. Photogrammetric processing of low-altitude images acquired by unpiloted aerial vehicles. Photogramm. Rec. 2011, 26, 190–211. [Google Scholar] [CrossRef]
- Pajares, G. Overview and current status of remote sensing applications based on unmanned aerial vehicles (UAVs). Photogramm. Eng. Remote Sens. 2015, 81, 281–330. [Google Scholar] [CrossRef]
- Torres-Sánchez, J.; López-Granados, F.; de Castro, A.I.; Peña-Barragán, J.M. Configuration and specifications of an unmanned aerial vehicle (UAV) for early site specific weed management. PLoS ONE 2013, 8, e58210. [Google Scholar] [PubMed]
- Hengl, T. Finding the right pixel size. Comput. Geosci. 2006, 32, 1283–1298. [Google Scholar] [CrossRef]
- Peña, J.M.; Torres-Sánchez, J.; Serrano-Pérez, A.; de Castro, A.I.; López-Granados, F. Quantifying efficacy and limits of unmanned aerial vehicle (UAV) technology for weed seedling detection as affected by sensor resolution. Sensors 2015, 15, 5609–5626. [Google Scholar] [CrossRef] [PubMed]
- Eisenbeiss, H.; Sauerbier, M. Investigation of uav systems and flight modes for photogrammetric applications. Photogramm. Rec. 2011, 26, 400–421. [Google Scholar] [CrossRef]
- Rodriguez-Gonzalvez, P.; Gonzalez-Aguilera, D.; Lopez-Jimenez, G.; Picon-Cabrera, I. Image-based modeling of built environment from an unmanned aerial system. Automation Constr. 2014, 48, 44–52. [Google Scholar] [CrossRef]
- Eisenbeiss, H. The autonomous mini helicopter: A powerful platform for mobile mapping. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 977–983. [Google Scholar]
- Wang, J.; Ge, Y.; Heuvelink, G.B.M.; Zhou, C.; Brus, D. Effect of the sampling design of ground control points on the geometric correction of remotely sensed imagery. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 91–100. [Google Scholar] [CrossRef]
- Vega, F.A.; Ramírez, F.C.; Saiz, M.P.; Rosúa, F.O. Multi-temporal imaging using an unmanned aerial vehicle for monitoring a sunflower crop. Biosyst. Eng. 2015, 132, 19–27. [Google Scholar] [CrossRef]
- Turner, D.; Lucieer, A.; Watson, C. An automated technique for generating georectified mosaics from ultra-high resolution unmanned aerial vehicle (UAV) imagery, based on structure from motion (SFM) point clouds. Remote Sens. 2012, 4, 1392–1410. [Google Scholar] [CrossRef]
- Mesas-Carrascosa, F.J.; Clavero Rumbao, I.; Barrera Berrocal, J.A.; García-Ferrer Porras, A. Positional quality assessment of orthophotos obtained from sensors onboard multi-rotor UAV platforms. Sensors 2014, 14, 22394–22407. [Google Scholar] [CrossRef]
- Primicerio, J.; di Gennaro, S.; Fiorillo, E.; Genesio, L.; Lugato, E.; Matese, A.; Vaccari, F. A flexible unmanned aerial vehicle for precision agriculture. Precis. Agric. 2012, 13, 517–523. [Google Scholar] [CrossRef]
- Hruska, R.; Mitchell, J.; Anderson, M.; Glenn, N.F. Radiometric and geometric analysis of hyperspectral imagery acquired from an unmanned aerial vehicle. Remote Sens. 2012, 4, 2736–2752. [Google Scholar] [CrossRef]
- Möller, M.; Alchanatis, V.; Cohen, Y.; Meron, M.; Tsipris, J.; Naor, A.; Ostrovsky, V.; Sprintsin, M.; Cohen, S. Use of thermal and visible imagery for estimating crop water status of irrigated grapevine. J. Exp. Bot. 2007, 58, 827–838. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Candón, D.; de Castro, A.I.; López-Granados, F. Assessing the accuracy of mosaics from unmanned aerial vehicle (UAV) imagery for precision agriculture purposes in wheat. Precis. Agric. 2014, 15, 44–56. [Google Scholar] [CrossRef]
- Torres-Sánchez, J.; Peña, J.M.; de Castro, A.I.; López-Granados, F. Multi-temporal mapping of the vegetation fraction in early-season wheat fields using images from UAV. Comput. Electron. Agric. 2014, 103, 104–113. [Google Scholar] [CrossRef]
- Hunt, E.R.; Hively, W.D.; Fujikawa, S.; Linden, D.; Daughtry, C.S.; McCarty, G. Acquisition of nir-green-blue digital photographs from unmanned aircraft for crop monitoring. Remote Sens. 2010, 2, 290–305. [Google Scholar] [CrossRef]
- Huang, Y.; Thomson, S.J.; Lan, Y.; Maas, S.J. Multispectral imaging systems for airborne remote sensing to support agricultural production management. Int. J. Agric. Biol. Eng. 2010, 3, 50–62. [Google Scholar]
- Kelcey, J.; Lucieer, A. Sensor correction of a 6-band multispectral imaging sensor for UAV remote sensing. Remote Sens. 2012, 4, 1462–1493. [Google Scholar] [CrossRef]
- Tetracam. Pixelwrench 2. Available online: http://www.Tetracam.Com/pdfs/pw2%20faq.Pdf (accessed on 17 June 2015).
- Meier, U. Growth Stages of Mono- and Dicotyledonous Plants. Bb Monograph. Available online: http://www.bba.de/veroeff/bbch/bbcheng.pdf (accessed on 17 June 2015).
- Kraus, K. Photogrammetry—Geometry from Images and Laser Scans; Walter de Gruyter: Goettingen, Germany, 2007. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Snavely, N.; Garg, R.; Seitz, S.M.; Szeliski, R. Finding paths through the world’s photos. ACM Trans. Graph. 2008, 27, 1–11. [Google Scholar] [CrossRef]
- Aber, J.S.; Marzolff, I.; Ries, J.B. Chapter 3—Photogrammetry. In Small-Format Aerial Photography; Ries, J.S.A.M.B., Ed.; Elsevier: Amsterdam, The Netherlands, 2010; pp. 23–39. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Bemis, S.P.; Micklethwaite, S.; Turner, D.; James, M.R.; Akciz, S.; Thiele, S.T.; Bangash, H.A. Ground-based and UAV-based photogrammetry: A multi-scale, high-resolution mapping tool for structural geology and paleoseismology. J. Struct. Geol. 2014, 69, 163–178. [Google Scholar] [CrossRef]
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A Comparison and Evaluation of Multi-View Stereo Reconstruction Algorithms. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 17–22 June 2006; pp. 519–528.
- Furukawa, Y.; Ponce, J. Accurate, dense, and robust multiview stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1362–1376. [Google Scholar] [CrossRef] [PubMed]
- International Organization for Standardization (ISO). Geographic Information—Data Quality; ISO: London, UK, 2013. [Google Scholar]
- Ariza Lopez, F.J.; Atkinson Gordo, A.D.; Rodriguez Avi, J. Acceptance curves for the positional control of geographic databases. J. Surv. Eng. 2008, 134, 26–32. [Google Scholar] [CrossRef]
- American Society of Photogrammetry and Remote Sensing (ASPRS). ASPRS Positional Accuracy Standards for Digital Geospatial Data; ASPRS: Bethesda, MA, USA, 2014. [Google Scholar]
- US Army Corps of Engineers (USACE). Engineering and Design. Photogrammetric Mapping; USACE: Washington, DC, USA, 2002. [Google Scholar]
- Practice, D.O.D.S. Mapping, Charting and Geodesy Accuracy. Available online: http://earth-info.nga.mil/publications/specs/printed/600001/600001_Accuracy.pdf (accessed on 25 September 2015).
- Kaufman, Y.J.; Remer, L.A. Detection of forests using mid-IR reflectance: An application for aerosol studies. IEEE Trans. Geosci. Remote Sens. 1994, 32, 672–683. [Google Scholar] [CrossRef]
- Baltsavias, E.P. A comparison between photogrammetry and laser scanning. ISPRS J. Photogramm. Remote Sens. 1999, 54, 83–94. [Google Scholar] [CrossRef]
- Ruzgienė, B.; Berteška, T.; Gečyte, S.; Jakubauskienė, E.; Aksamitauskas, V.Č. The surface modelling based on uav photogrammetry and qualitative estimation. Measurement 2015, 73, 619–627. [Google Scholar]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. “Structure-from-motion” photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef] [Green Version]
- Orti, F. Optimal distribution of control points to minimize Landsat image registration errors. Photogramm. Eng. Remote Sens. 1981, 47, 101–110. [Google Scholar]
- Verbeke, J.; Hulens, D.; Ramon, H.; Goedeme, T.; de Schutter, J. The design and construction of a high endurance hexacopter suited for narrow corridors. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 543–551.
- Gatti, M.; Giulietti, F. Preliminary design analysis methodology for electric multirotor. In Proceedings of the RED-UAS 2013, 2nd IFAC Workshop Research, Education and Development of Unmanned Aerial Systems, Compiegne, France, 20–22 November 2013; pp. 58–63.
- Forster, B.C.; Best, P. Estimation of spot p-mode point spread function and derivation of a deconvolution filter. ISPRS J. Photogramm. Remote Sens. 1994, 49, 32–42. [Google Scholar] [CrossRef]
- Peña-Barragán, J.M.; Ngugi, M.K.; Plant, R.E.; Six, J. Object-based crop identification using multiple vegetation indices, textural features and crop phenology. Remote Sens. Environ. 2011, 115, 1301–1316. [Google Scholar] [CrossRef]
- Torres-Sánchez, J.; López-Granados, F.; Peña, J.M. An automatic object-based method for optimal thresholding in UAV images: Application for vegetation detection in herbaceous crops. Comput. Electron. Agric. 2015, 114, 43–52. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mesas-Carrascosa, F.-J.; Torres-Sánchez, J.; Clavero-Rumbao, I.; García-Ferrer, A.; Peña, J.-M.; Borra-Serrano, I.; López-Granados, F. Assessing Optimal Flight Parameters for Generating Accurate Multispectral Orthomosaicks by UAV to Support Site-Specific Crop Management. Remote Sens. 2015, 7, 12793-12814. https://doi.org/10.3390/rs71012793
Mesas-Carrascosa F-J, Torres-Sánchez J, Clavero-Rumbao I, García-Ferrer A, Peña J-M, Borra-Serrano I, López-Granados F. Assessing Optimal Flight Parameters for Generating Accurate Multispectral Orthomosaicks by UAV to Support Site-Specific Crop Management. Remote Sensing. 2015; 7(10):12793-12814. https://doi.org/10.3390/rs71012793
Chicago/Turabian StyleMesas-Carrascosa, Francisco-Javier, Jorge Torres-Sánchez, Inmaculada Clavero-Rumbao, Alfonso García-Ferrer, Jose-Manuel Peña, Irene Borra-Serrano, and Francisca López-Granados. 2015. "Assessing Optimal Flight Parameters for Generating Accurate Multispectral Orthomosaicks by UAV to Support Site-Specific Crop Management" Remote Sensing 7, no. 10: 12793-12814. https://doi.org/10.3390/rs71012793
APA StyleMesas-Carrascosa, F. -J., Torres-Sánchez, J., Clavero-Rumbao, I., García-Ferrer, A., Peña, J. -M., Borra-Serrano, I., & López-Granados, F. (2015). Assessing Optimal Flight Parameters for Generating Accurate Multispectral Orthomosaicks by UAV to Support Site-Specific Crop Management. Remote Sensing, 7(10), 12793-12814. https://doi.org/10.3390/rs71012793