Comparison of the Continuity of Vegetation Indices Derived from Landsat 8 OLI and Landsat 7 ETM+ Data among Different Vegetation Types
Abstract
:1. Introduction
2. Data
2.1. Ground Experimental Data
2.2. Satellite Data

| Seasons | Path/Row: 45/32 | Path/Row: 35/38 | ||
|---|---|---|---|---|
| Landsat 7 ETM+ | Landsat 8 OLI | Landsat 7 ETM+ | Landsat 8 OLI | |
| Spring | LE72013121 (1 May 2013) | LC8 2013113 (24 April 2013) | LE7 2014070 (11 March 2014) | LC8 2014078 (19 March 2014) |
| Summer | LE7 2013201 (20 July 2013) | LC8 2013193 (12 July 2013) | LE7 2014182 (1 July 2014) | LC8 2014174 (23 June 2014) |
| Autumn | LE7 2013249 (6 September 2013) | LC8 2013257 (12 September 2013) | LE7 2013275 (2 October 2013) | LC8 2013267 (24 September 2013) |
| Winter | LE7 2013329 (25 November 2013) | LC8 2013337 (3 December 2013) | LE7 2014006 (6 January 2014) | LC8 2014014 (14 January 2014) |
3. Methodology

3.1. Simulated Data Process

3.2. Satellite Data Process

3.3. Vegetation Indices
4. Results
4.1. Continuity of VIs Derived from Simulated Data
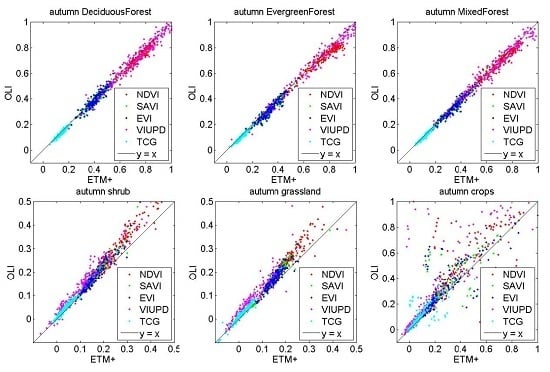
4.2. Continuity of VIs Derived from Satellite Data




4.2.1. Analysis of the Generation Algorithm for VIs
| -- | NDVI | SAVI | EVI | VIUPD | TCG | |
|---|---|---|---|---|---|---|
| Spring | Deciduous Forest | Y = 0.97 x − 0.017 | Y = 0.98 x − 0.027 | Y = 0.95 x − 0.024 | Y = 1.03 x − 0.095 | Y = 0.91 x − 0.015 |
| Evergreen Forest | Y = 0.93 x + 0.029 | Y = 0.94 x + 0.003 | Y = 0.92 x + 0.005 | Y = 0.96 x + 0.004 | Y = 0.88 x − 0.003 | |
| Mixed Forest | Y = 0.89 x + 0.052 | Y = 0.91 x + 0.010 | Y = 0.89 x + 0.009 | Y = 0.94 x − 0.003 | Y = 0.85 x − 0.0003 | |
| Shrub | Y = 0.96 x + 0.015 | Y = 0.95 x + 0.014 | Y = 0.94 x + 0.012 | Y = 0.92 x + 0.007 | Y = 0.98 x − 0.008 | |
| Grassland | Y = 1.12 x − 0.001 | Y = 1.10 x + 0.001 | Y = 1.05 x + 0.004 | Y = 1.10 x + 0.014 | Y = 1.17 x − 0.013 | |
| Crops | Y = 1.06 x + 0.017 | Y = 1.10 x + 0.014 | Y = 0.98 x + 0.021 | Y = 1.07 x + 0.025 | Y = 1.03 x − 0.004 | |
| Summer | Deciduous Forest | Y = 0.95 x + 0.047 | Y = 0.996 x + 0.01 | Y = 0.98 x + 0.011 | Y = 0.99 x + 0.018 | Y = 0.96 x + 0.001 |
| Evergreen Forest | Y = 0.98 x + 0.011 | Y = 1.01 x − 0.002 | Y = 0.99 x − 0.003 | Y = 0.995 x − 0.008 | Y = 0.97 x − 0.004 | |
| Mixed Forest | Y = 0.92 x + 0.060 | Y = 0.97 x + 0.018 | Y = 0.97 x + 0.011 | Y = 0.97 x + 0.020 | Y = 0.93 x + 0.003 | |
| Shrub | Y = 1.06 x + 0.006 | Y = 1.05 x + 0.005 | Y = 1.03 x + 0.005 | Y = 1.03 x + 0.013 | Y = 1.02 x − 0.008 | |
| Grassland | Y = 0.87 x + 0.030 | Y = 0.82 x + 0.030 | Y = 0.73 x + 0.04 | Y = 0.79 x + 0.010 | Y = 0.99 x − 0.013 | |
| Crops | Y = 0.85 x + 0.053 | Y = 0.81 x + 0.051 | Y = 0.72 x + 0.06 | Y = 0.75 x + 0.044 | Y = 0.79 x + 0.005 | |
| Autumn | Deciduous Forest | Y = 0.93 x + 0.035 | Y = 1.00 x − 0.012 | Y = 0.997 x − 0.01 | Y = 0.95 x + 0.020 | Y = 0.94 x − 0.008 |
| Evergreen Forest | Y = 0.89 x + 0.056 | Y = 1.02 x − 0.022 | Y = 1.01 x − 0.021 | Y = 0.93 x + 0.032 | Y = 0.96 x − 0.011 | |
| Mixed Forest | Y = 0.90 x + 0.055 | Y = 0.97 x + 0.001 | Y = 0.98 x − 0.005 | Y = 0.94 x + 0.027 | Y = 0.91 x − 0.002 | |
| Shrub | Y = 1.18 x − 0.004 | Y = 1.19 x − 0.006 | Y = 1.16 x − 0.005 | Y = 1.17 x + 0.017 | Y = 1.17 x − 0.008 | |
| Grassland | Y = 1.17 x + 0.003 | Y = 1.10 x + 0.010 | Y = 1.02 x + 0.019 | Y = 1.09 x + 0.028 | Y = 1.20 x − 0.011 | |
| Crops | Y = 0.87 x + 0.125 | Y = 0.81 x + 0.094 | Y = 0.75 x + 0.105 | Y = 0.84 x + 0.124 | Y = 0.78 x + 0.030 | |
| Winter | Deciduous Forest | Y = 0.90 x + 0.072 | Y = 1.07 x − 0.023 | Y = 1.03 x − 0.021 | Y = 0.98 x + 0.037 | Y = 0.995 x − 0.006 |
| Evergreen Forest | Y = 0.79 x + 0.157 | Y = 1.09 x − 0.034 | Y = 1.06 x − 0.032 | Y = 0.92 x + 0.102 | Y = 1.01 x − 0.010 | |
| Mixed Forest | Y = 0.88 x + 0.086 | Y = 1.08 x − 0.024 | Y = 1.05 x − 0.024 | Y = 0.98 x + 0.036 | Y = 1.00 x − 0.006 | |
| Shrub | Y = 1.00 x + 0.008 | Y = 0.99 x + 0.006 | Y = 0.94 x + 0.008 | Y = 0.92 x + 0.004 | Y = 1.01 x − 0.009 | |
| Grassland | Y = 0.97 x + 0.012 | Y = 0.95 x + 0.011 | Y = 0.89 x + 0.014 | Y = 0.96 x + 0.007 | Y = 1.08 x − 0.014 | |
| Crops | Y = 1.06 x + 0.002 | Y = 1.04 x + 0.005 | Y = 0.98 x + 0.009 | Y = 1.07 x + 0.008 | Y = 1.03 x − 0.009 | |
| Seasons | Vegetation Types | NDVI | SAVI | EVI | VIUPD | TCG |
|---|---|---|---|---|---|---|
| Spring | Deciduous Forest | 0.7421 | 0.7364 | 0.734 | 0.7968 | 0.7609 |
| Evergreen Forest | 0.9314 | 0.9117 | 0.9015 | 0.9502 | 0.9201 | |
| Mixed Forest | 0.8031 | 0.8234 | 0.8263 | 0.8616 | 0.8376 | |
| Shrub | 0.8898 | 0.8299 | 0.8312 | 0.9199 | 0.883 | |
| Grassland | 0.9411 | 0.9406 | 0.9362 | 0.9486 | 0.9616 | |
| crops | 0.9442 | 0.9487 | 0.9503 | 0.9518 | 0.9512 | |
| Summer | Deciduous Forest | 0.9272 | 0.9326 | 0.9187 | 0.9584 | 0.936 |
| Evergreen Forest | 0.9606 | 0.9623 | 0.9527 | 0.9736 | 0.9643 | |
| Mixed Forest | 0.9294 | 0.9498 | 0.9444 | 0.9621 | 0.9561 | |
| Shrub | 0.9155 | 0.9008 | 0.9004 | 0.9339 | 0.9176 | |
| Grassland | 0.8659 | 0.8694 | 0.8596 | 0.8692 | 0.9333 | |
| crops | 0.7475 | 0.6799 | 0.6277 | 0.6675 | 0.657 | |
| Autumn | Deciduous Forest | 0.9252 | 0.937 | 0.9247 | 0.9564 | 0.9441 |
| Evergreen Forest | 0.9403 | 0.9402 | 0.9347 | 0.9642 | 0.9492 | |
| Mixed Forest | 0.9453 | 0.9561 | 0.9501 | 0.9685 | 0.96 | |
| Shrub | 0.9503 | 0.9425 | 0.9376 | 0.9615 | 0.9468 | |
| Grassland | 0.8847 | 0.839 | 0.7692 | 0.8201 | 0.9217 | |
| crops | 0.6376 | 0.6038 | 0.5847 | 0.5768 | 0.6103 | |
| Winter | Deciduous Forest | 0.8317 | 0.9311 | 0.9266 | 0.9072 | 0.9407 |
| Evergreen Forest | 0.6968 | 0.9446 | 0.9407 | 0.8408 | 0.9552 | |
| Mixed Forest | 0.8016 | 0.9622 | 0.9564 | 0.886 | 0.9652 | |
| Shrub | 0.8768 | 0.841 | 0.8184 | 0.8818 | 0.899 | |
| Grassland | 0.9215 | 0.9171 | 0.9164 | 0.9535 | 0.9589 | |
| crops | 0.9716 | 0.9773 | 0.9771 | 0.957 | 0.9773 |



4.2.2. The Response of VIs to Growth Variation
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
| Path/Row: 45/32 | Path/Row: 35/38 | ||
|---|---|---|---|
| Landsat 8 OLI | Landsat 7 ETM+ | Landsat 8 OLI | Landsat 7 ETM+ |
| LC82013113 | LE72013121 | LC82013123 | LE72013115 |
| LC82013145 | LE72013153 | LC82013139 | LE72013163 |
| LC82013193 | LE72013185 | LC82013155 | LE72013195 |
| LC82013209 | LE72013201 | LC82013171 | LE72013227 |
| LC82013225 | LE72013217 | LC82013187 | LE72013243 |
| LC82013241 | LE72013233 | LC82013267 | LE72013259 |
| LC82013257 | LE72013249 | LC82013299 | LE72013275 |
| LC82013305 | LE72013297 | LC82013315 | LE72013291 |
| LC82013321 | LE72013313 | LC82013347 | LE72014006 |
| LC82013337 | LE72013329 | LC82013363 | LE72014038 |
| LC82013353 | LE72014076 | LC82014014 | LE72014070 |
| LC82014004 | LE72014156 | LC82014046 | LE72014086 |
| LC82014020 | LE72014172 | LC82014078 | LE72014118 |
| LC82014052 | LE72014188 | LC82014094 | LE72014134 |
| LC82014100 | LE72014220 | LC82014110 | LE72014150 |
| LC82014132 | LE72014236 | LC82014126 | LE72014166 |
| LC82014148 | LE72014284 | LC82014142 | LE72014182 |
| LC82014164 | -- | LC82014158 | LE72014278 |
| LC82014180 | -- | LC82014174 | LE72014326 |
| LC82014212 | -- | LC82014190 | -- |
| LC82014228 | -- | LC82014206 | -- |
| LC82014244 | -- | LC82014254 | -- |
| LC82014276 | -- | LC82014286 | -- |
| -- | -- | LC82014302 | -- |
| -- | -- | LC82014334 | -- |
| 40 scenes in total | 44 scenes in total | ||
References
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Main-Knorn, M.; Cohen, W.B.; Kennedy, R.E.; Grodzki, W.; Pflugmacher, D.; Griffiths, P.; Hostert, P. Monitoring coniferous forest biomass change using a Landsat trajectory-based approach. Remote Sens. Environ. 2013, 139, 277–290. [Google Scholar] [CrossRef]
- Fraser, R.H.; Olthof, I.; Carrière, M.; Deschamps, A.; Pouliot, D. Detecting long-term changes to vegetation in northern Canada using the Landsat satellite image archive. Environ. Res. Lett. 2011, 6. Available online: http://iopscience.iop.org/article/10.1088/1748-9326/6/4/045502/meta;jsessionid=A6AAB78709ADF04988163217D910E3DD.c1 (accessed on 10 June 2015). [Google Scholar] [CrossRef]
- Melaas, E.K.; Friedl, M.A.; Zhu, Z. Detecting interannual variation in deciduous broadleaf forest phenology using Landsat TM/ETM+ data. Remote Sens. Environ. 2013, 132, 176–185. [Google Scholar] [CrossRef]
- Hostert, P.; Röder, A.; Hill, J. Coupling spectral unmixing and trend analysis for monitoring of long-term vegetation dynamics in Mediterranean rangelands. Remote Sens. Environ. 2003, 87, 183–197. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Jackson, R.D.; Huete, A.R. Interpreting vegetation indices. Prev. Vet. Med. 1991, 11, 185–200. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Trishchenko, A.P. Effects of spectral response function on surface reflectance and NDVI measured with moderate resolution satellite sensors: Extension to AVHRR NOAA-17, 18 and METOP-A. Remote Sens. Environ. 2009, 113, 335–341. [Google Scholar] [CrossRef]
- Gallo, K.; Ji, L.; Reed, B.; Eidenshink, J.; Dwyer, J. Multi-platform comparisons of MODIS and AVHRR normalized difference vegetation index data. Remote Sens. Environ. 2005, 99, 221–231. [Google Scholar] [CrossRef]
- Teillet, P.M.; Barker, J.L.; Markham, B.L.; Irish, R.R.; Fedosejevs, G.; Storey, J.C. Radiometric cross-calibration of the Landsat-7 ETM+ and Landsat-5 TM sensors based on tandem data sets. Remote Sens. Environ. 2001, 78, 39–54. [Google Scholar] [CrossRef]
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
- Miura, T.; Huete, A.R.; Yoshioka, H. Evaluation of sensor calibration uncertainties on vegetation indices for MODIS. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1399–1409. [Google Scholar] [CrossRef]
- Brown, M.E.; Pinzón, J.E.; Didan, K.; Tucker, J.T.M.C.J. Evaluation of the consistency of long-term NDVI time series derived from AVHRR,SPOT-vegetation, SeaWiFS, MODIS, and Landsat ETM+ sensors. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1787–1793. [Google Scholar] [CrossRef]
- Hill, J.; Aifadopoulou, D. Comparative analysis of Landsat-5 TM and spot HRV-1 data for use in multiple sensor approaches. Remote Sens. Environ. 1990, 34, 55–70. [Google Scholar] [CrossRef]
- Gallo, K. Comparison of MODIS and AVHRR 16-day normalized difference vegetation index composite data. Geophys. Res. Lett. 2004, 31, 455–467. [Google Scholar] [CrossRef]
- Steven, M.D.; Malthus, T.J.; Baret, F.; Xu, H.; Chopping, M.J. Intercalibration of vegetation indices from different sensor systems. Remote Sens. Environ. 2003, 88, 412–422. [Google Scholar] [CrossRef]
- Tarnavsky, E.; Garrigues, S.; Brown, M.E. Multiscale geostatistical analysis of AVHRR, SPOT-VGT, and MODIS global NDVI products. Remote Sens. Environ. 2008, 112, 535–549. [Google Scholar] [CrossRef]
- Swinnen, E.; Veroustraete, F. Extending the SPOT-VEGETATION NDVI time series (1998–2006) back in time with NOAA-AVHRR data (1985–1998) for southern Africa. IEEE Trans. Geosci. Remote Sens. 2008, 46, 558–572. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, L.; Zhang, X.; Liu, B. Comparison of the sensor dependence of vegetation indices based on Hyperion and CHRIS hyperspectral data. Int. J. Remote Sens. 2013, 34, 2200–2215. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Lyon, J.G.; Huete, A. Hyperspectral Remote Sensing of Vegetation; CRC Press: New York, NY, USA, 2011. [Google Scholar]
- Meroni, M.; Atzberger, C.; Vancutsem, C.; Gobron, N.; Baret, F.; Lacaze, R.; Eerens, H.; Leo, O. Evaluation of agreement between space remote sensing SPOT-VEGETATION fAPAR time series. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1951–1961. [Google Scholar] [CrossRef]
- Arvidsona, T.; Gaschb, J.; Gowardc, S.N. Landsat 7’s long-term acquisition plan—An innovative approach to building a global imagery archive. Remote Sens. Environ. 2001, 78, 13–26. [Google Scholar] [CrossRef]
- Irons, J.R.; Dwyer, J.L.; Barsi, J.A. The next Landsat satellite: The Landsat data continuity mission. Remote Sens. Environ. 2012, 122, 11–21. [Google Scholar] [CrossRef]
- Williams, D.L.; Goward, S.; Arvidson, T. Landsat yesterday, today, and tomorrow. Photogramm. Eng. Remote Sens. 2006, 72, 1171–1178. [Google Scholar] [CrossRef]
- Markham, B.L.; Storey, J.C.; Williams, D.L.; Irons, J.R. Landsat sensor performance: History and current status. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2691–2694. [Google Scholar] [CrossRef]
- Flood, N. Continuity of Reflectance Data between Landsat-7 ETM+ and Landsat-8 OLI, for both top-of-atmosphere and surface reflectance: A Study in the Australian landscape. Remote Sens. 2014, 6, 7952–7970. [Google Scholar] [CrossRef]
- Markham, B.; Barsi, J.; Kvaran, G.; Ong, L.; Kaita, E.; Biggar, S.; Czapla-Myers, J.; Mishra, N.; Helder, D. Landsat-8 operational land imager radiometric calibration and stability. Remote Sens. 2014, 6, 12275–12308. [Google Scholar] [CrossRef]
- Czapla-Myers, J.; McCorkel, J.; Anderson, N.; Thome, K.; Biggar, S.; Helder, D.; Aaron, D.; Leigh, L.; Mishra, N. The ground-based absolute radiometric calibration of Landsat 8 OLI. Remote Sens. 2015, 7, 600–626. [Google Scholar] [CrossRef]
- Morfitt, R.; Barsi, J.; Levy, R.; Markham, B.; Micijevic, E.; Ong, L.; Scaramuzza, P.; Vanderwerff, K. Landsat-8 Operational Land Imager (OLI) radiometric performance on-orbit. Remote Sens. 2015, 7, 2208–2237. [Google Scholar] [CrossRef]
- Knight, E.; Kvaran, G. Landsat-8 operational land imager design, characterization and performance. Remote Sens. 2014, 6, 10286–10305. [Google Scholar] [CrossRef]
- Li, P.; Jiang, L.; Feng, Z. Cross-Comparison of Vegetation Indices Derived from Landsat-7 Enhanced Thematic Mapper Plus (ETM+) and Landsat-8 Operational Land Imager (OLI) sensors. Remote Sens. 2013, 6, 310–329. [Google Scholar] [CrossRef]
- Zhang, L.; Fujiwara, N.; Furumi, S.; Muramatsu, K.; Daigo, M.; Zhang, L. Assessment of the universal pattern decomposition method using MODIS and ETM+ data. Int. J. Remote Sens. 2007, 28, 125–142. [Google Scholar] [CrossRef]
- Ke, Y.; Im, J.; Lee, J.; Gong, H.; Ryu, Y. Characteristics of Landsat 8 OLI-derived NDVI by comparison with multiple satellite sensors and in-situ observations. Remote Sens. Environ. 2015, 164, 298–313. [Google Scholar] [CrossRef]
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Liu, H.Q.; Huete, A. A feedback based modification of the NDV I to minimize canopy background and atmospheric noise. IEEE Trans. Geosci. Remote Sens. 1995, 33, 457–465. [Google Scholar]
- Zhang, L.; Furumi, S.; Muramatsu, K.; Fujiwara, N.; Daigo, M.; Zhang, L. A new vegetation index based on the universal pattern decomposition method. Int. J. Remote Sens. 2007, 28, 107–124. [Google Scholar] [CrossRef]
- Kauth, R.J.; Thomas, G.S. The Tasselled Cap—A graphic description of the spectral-temporal development of agricultural crops as seen by Landsat. In Proceedings of the Laboratory for Applications of Remote Sensing Symposia, Nashua, NH, USA, 29 June–1 July 1976.
- Miura, T.; Huete, A.; Yoshioka, H. An empirical investigation of cross-sensor relationships of NDVI and red/near-infrared reflectance using EO-1 Hyperion data. Remote Sens. Environ. 2006, 100, 223–236. [Google Scholar] [CrossRef]
- Zhang, L.; Furumi, S.; Muramatsu, K.; Fujiwara, N.; Daigo, M.; Zhang, L. Sensor-independent analysis method for hyperspectral data based on the pattern decomposition method. Int. J. Remote Sens. 2006, 27, 4899–4910. [Google Scholar] [CrossRef]
- She, X.; Zhang, L.; Baig, M.H.A.; Li, Y. Calculating vegetation index based on the universal pattern decomposition method (VIUPD) using Landsat 8. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 4734–4737.
- Huang, C.; Wylie, B.; Yang, L.; Homer, C.; Zylstra, G. Derivation of a tasselled cap transformation based on Landsat 7 at-satellite reflectance. Int. J. Remote Sens. 2002, 23, 1741–1748. [Google Scholar] [CrossRef]
- Baig, M.H.A.; Zhang, L.; Shuai, T.; Tong, Q. Derivation of a tasselled cap transformation based on Landsat 8 at-satellite reflectance. Remote Sens. Lett. 2014, 5, 423–431. [Google Scholar] [CrossRef]
- Wardlow, B.; Egbert, S.; Kastens, J. Analysis of time-series MODIS 250 m vegetation index data for crop classification in the U.S. Central Great Plains. Remote Sens. Environ. 2007, 108, 290–310. [Google Scholar] [CrossRef]
- Roy, D.P.; Ju, J.; Lewis, P.; Schaaf, C.; Gao, F.; Hansen, M.; Lindquist, E. Multi-temporal MODIS–Landsat data fusion for relative radiometric normalization, gap filling, and prediction of Landsat data. Remote Sens. Environ. 2008, 112, 3112–3130. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
She, X.; Zhang, L.; Cen, Y.; Wu, T.; Huang, C.; Baig, M.H.A. Comparison of the Continuity of Vegetation Indices Derived from Landsat 8 OLI and Landsat 7 ETM+ Data among Different Vegetation Types. Remote Sens. 2015, 7, 13485-13506. https://doi.org/10.3390/rs71013485
She X, Zhang L, Cen Y, Wu T, Huang C, Baig MHA. Comparison of the Continuity of Vegetation Indices Derived from Landsat 8 OLI and Landsat 7 ETM+ Data among Different Vegetation Types. Remote Sensing. 2015; 7(10):13485-13506. https://doi.org/10.3390/rs71013485
Chicago/Turabian StyleShe, Xiaojun, Lifu Zhang, Yi Cen, Taixia Wu, Changping Huang, and Muhammad Hasan Ali Baig. 2015. "Comparison of the Continuity of Vegetation Indices Derived from Landsat 8 OLI and Landsat 7 ETM+ Data among Different Vegetation Types" Remote Sensing 7, no. 10: 13485-13506. https://doi.org/10.3390/rs71013485
APA StyleShe, X., Zhang, L., Cen, Y., Wu, T., Huang, C., & Baig, M. H. A. (2015). Comparison of the Continuity of Vegetation Indices Derived from Landsat 8 OLI and Landsat 7 ETM+ Data among Different Vegetation Types. Remote Sensing, 7(10), 13485-13506. https://doi.org/10.3390/rs71013485