Flood Hazard Mapping Combining Hydrodynamic Modeling and Multi Annual Remote Sensing data

Abstract

This paper explores a method to combine the time and space continuity of a large-scale inundation model with discontinuous satellite microwave observations, for high-resolution flood hazard mapping. The assumption behind this approach is that hydraulic variables computed from continuous spatially-distributed hydrodynamic modeling and observed as discrete satellite-derived flood extents are correlated in time, so that probabilities can be transferred from the model series to the observations. A prerequisite is, therefore, the existence of a significant correlation between a modeled variable (i.e., flood extent or volume) and the synchronously-observed flood extent. If this is the case, the availability of model simulations over a long time period allows for a robust estimate of non-exceedance probabilities that can be attributed to corresponding synchronously-available satellite observations. The generated flood hazard map has a spatial resolution equal to that of the satellite images, which is higher than that of currently available large scale inundation models. The method was applied on the Severn River (UK), using the outputs of a global inundation model provided by the European Centre for Medium-range Weather Forecasts and a large collection of ENVISAT ASAR imagery. A comparison between the hazard map obtained with the proposed method and with a more traditional numerical modeling approach supports the hypothesis that combining model results and satellite observations could provide advantages for high-resolution flood hazard mapping, provided that a sufficient number of remote sensing images is available and that a time correlation is present between variables derived from a global model and obtained from satellite observations.

1. Introduction

In the framework of a comprehensive and standardized flood risk management at the global scale, the development of a remote sensing-based flood hazard mapping method is of primary interest. Hazard maps are needed to enhance flood preparedness at large scale and to improve the services provided for crisis response and mitigation. This type of information is requested by globally operating insurance agencies and humanitarian relief organizations, among others.

In recent years different modeling approaches have been developed to derive global flood risk and/or hazard maps [1]. For example, global hazard maps have been obtained by using readily-available geomorphological indices (e.g., [2]) or by applying a simplified river routing model to map flood extent (e.g., [3,4]) (Table 1). Recently, Pappenberger et al. [5] estimated global flood hazard through a physical model cascade, here named PDWC2012, consisting of an atmospheric model linked to a coupled hydrologic-hydraulic model and forced with ERA-Interim reanalysed meteorological data. It performs continuous hydrologic and hydraulic simulations for the entire globe on a 25 km grid which is then re-projected onto a 1 km grid to derive maps of higher resolution. The advantage of this approach is that it uses globally-available precipitation and evapotranspiration data as inputs to a process-based hydrologic-hydraulic model to generate global flood inundation maps over long periods. PDWC2012 produces realistic hazard maps for the globe; however, its current resolution of 1 km limits its interest for smaller regions. In a similar way, but restricted to the European continent, Alfieri et al. [6] introduced the use of observed meteorological data to generate a long-term streamflow time series, from which design hydrographs are derived and used as forcings for a combined distributed hydrologic and hydraulic model. However, as the use of the design hyetograph and/or the design hydrograph constitutes one of the main sources of uncertainty, in the recent literature the use of continuous hydrologic and hydraulic simulations has been introduced [7,8,9].

A flood hazard mapping approach purely based on satellite observations would be welcome by the scientific community, as it would have the merit of being accurate, robust, and applicable throughout the world, particularly in regions where ground observations are not available. However, this approach is currently limited by the fact that collected time series of images are discontinuous and that the time periods covered are not long enough to provide an estimate of flood inundation probability distributions.

More traditional approaches, based on field measurements and numerical models, are still preferred [6,10] to generate harmonized flood hazard maps of relatively high resolution. As of today, remote sensing-derived flood maps are mostly used for rapid mapping of floods during crisis [11,12,13,14,15,16,17] and, more rarely, for evaluating [18,19], re-calibrating [20,21,22,23], and updating flood inundation models [24,25,26].

Remote sensing has also been applied to map spatio-temporal variations of flood inundation. Sakamoto et al. [27] and Islam et al. [28] used Moderate-Resolution Imaging Spectroradiometer (MODIS) time-series imagery to map flood inundation frequency in the Cambodia and the Vietnamese Mekong Delta and in Bangladesh, respectively. Landsat imagery was used by Thomas et al. [29] to map annual inundation in Australia, while the combination of thermal (ASTER) and SAR (ENVISAT) data has been successfully used to delineate the maximum flood extent after the 2011 Tohoku (Japan) Tsunami and to monitor water receding in the following days [30]. Moving to a finer time-scale, COSMO-SkyMed images were used to monitor the evolution of inundation extent during a single flood event [31,32,33], affecting urban and vegetated areas, also. On a larger scale, the Dartmouth Flood Observatory (DFO) has produced global hazard maps based on observations [34]. However, DFO does not provide an estimate of inundation probability distributions, which are typically required for flood hazard mapping. These approaches examine time-series of different satellite images to produce inundation frequency maps, showing how often an area has been inundated in the past.

Table 1. Overview of some literature studies [2,3,4,5,6,7,29,31,32,33,34,35,36] using different approaches (modeling, remote sensing observations, or a combination of the two) for flood hazard mapping or to detect spatio-temporal variation of flood extent. The current study is added for the sake of completeness (RP: Return Period).

Reference	Final Product	Approach
Mehlhorn et al. [2]	nation-wide flood hazard map (RP: 50 to 500 years)	Modeling: Geomorphological Regression Method
Herold and Mouton [3]	global flood hazard map(RP: 100 years)	Modeling: hydrologic GIS processing on DEM
Winsemius et al. [4]	global flood hazard map	Modeling: global hydrological model + global flood-routing model + inundation downscaling routine
Pappenberger et al. [5]	global flood hazard map + daily global flood inundation maps over 30 years	Modeling: Land surface model HTESSEL + River routing CaMa-Flood
Alfieri et al. [6]	pan-European flood hazard map (RP: 100 years)	Modeling: LISFLOOD–ACC
Sakamoto et al. [7]	spatio-temporal variation of annual inundation extent Cambodia and the Vietnamese Mekong Delta	Remote sensing observations: MODIS time-series imagery (2000–2005)
Thomas et al. [29]	mapping annual inundation in central-eastern Australia	Remote sensing observations: Landsat images (1979–2006)
Pulvirenti et al. [31]	spatio-temporal variation of inundation extent in Italy	Remote sensing observations: Multitemporal COSMO-SkyMed data (flood in 2009)
Chini et al. [32]	spatio-temporal variation of inundation extent in Japan	Remote sensing observations: Multitemporal COSMO-SkyMed data (flood in 2011)
Pulvirenti et al. [33]	spatio-temporal variation of inundation extent in Italy	Remote sensing observations: Multitemporal COSMO-SkyMed data (flood in 2014)
Brakenridge [34]	global archive of flood events	Remote sensing observations: remote sensing sources + news, governmental and instrumental sources
Skakun et al. [35]	relative frequency of inundation (RFI) in Namibia	Remote sensing observations: Landsat images (1989-2012)
Huang et al. [36]	probability map of inundation in south-eastern Australia	Combination of remote sensing observations and gauged time-series data: MODIS time-series imagery (1983–2010) and discharge gauged data
Current study	hazard map in UK Severn catchment	Combination of remote sensing observations and modeled time-series data: ENVISAT time-series imagery (2007–2010) and daily global flood inundation maps over 30 years [5]

Table 1. Overview of some literature studies [2,3,4,5,6,7,29,31,32,33,34,35,36] using different approaches (modeling, remote sensing observations, or a combination of the two) for flood hazard mapping or to detect spatio-temporal variation of flood extent. The current study is added for the sake of completeness (RP: Return Period).

Reference	Final Product	Approach
Mehlhorn et al. [2]	nation-wide flood hazard map (RP: 50 to 500 years)	Modeling: Geomorphological Regression Method
Herold and Mouton [3]	global flood hazard map(RP: 100 years)	Modeling: hydrologic GIS processing on DEM
Winsemius et al. [4]	global flood hazard map	Modeling: global hydrological model + global flood-routing model + inundation downscaling routine
Pappenberger et al. [5]	global flood hazard map + daily global flood inundation maps over 30 years	Modeling: Land surface model HTESSEL + River routing CaMa-Flood
Alfieri et al. [6]	pan-European flood hazard map (RP: 100 years)	Modeling: LISFLOOD–ACC
Sakamoto et al. [7]	spatio-temporal variation of annual inundation extent Cambodia and the Vietnamese Mekong Delta	Remote sensing observations: MODIS time-series imagery (2000–2005)
Thomas et al. [29]	mapping annual inundation in central-eastern Australia	Remote sensing observations: Landsat images (1979–2006)
Pulvirenti et al. [31]	spatio-temporal variation of inundation extent in Italy	Remote sensing observations: Multitemporal COSMO-SkyMed data (flood in 2009)
Chini et al. [32]	spatio-temporal variation of inundation extent in Japan	Remote sensing observations: Multitemporal COSMO-SkyMed data (flood in 2011)
Pulvirenti et al. [33]	spatio-temporal variation of inundation extent in Italy	Remote sensing observations: Multitemporal COSMO-SkyMed data (flood in 2014)
Brakenridge [34]	global archive of flood events	Remote sensing observations: remote sensing sources + news, governmental and instrumental sources
Skakun et al. [35]	relative frequency of inundation (RFI) in Namibia	Remote sensing observations: Landsat images (1989-2012)
Huang et al. [36]	probability map of inundation in south-eastern Australia	Combination of remote sensing observations and gauged time-series data: MODIS time-series imagery (1983–2010) and discharge gauged data
Current study	hazard map in UK Severn catchment	Combination of remote sensing observations and modeled time-series data: ENVISAT time-series imagery (2007–2010) and daily global flood inundation maps over 30 years [5]

As shown in Table 1 [2,3,4,5,6,7,29,31,32,33,34,35,36], flood hazard maps are usually computed with hydrodynamic modeling. However, in the framework of global applications, flood hazard maps currently available for the entire globe tend to be characterized by a rather coarse resolution. On the other hand, remote sensing observations do have a higher spatial resolution but, before the advent of the Sentinel mission, acquisition of images was non-regular in time. As a consequence, the collected time series could not be used for statistical analysis, but rather to compute the frequency of inundation.

Due to the aforementioned limitations of existing methods, a step change in flood hazard mapping could be achieved by combining discontinuous (and typically short) series of remote sensing-derived flood inundation maps with a (long) time-continuous series of hydrological data. The assumption behind this approach is that observed inundations in the discontinuous series show a good correlation with the synchronous values of the hydrological variable in the continuous series. This has been proven true for the relationship between inundation and river discharge [37] and for the relationship between inundation and water height [38].

Huang et al. [36] combined remotely-sensed data obtained with MODIS and gauge observations of discharge, to derive a flood probability map over the Murray-Darling basin in Australia. The first step of their procedure is the selection of a point measurement, e.g., a stream gauge, which is assumed to be representative of a predefined floodable area. The choice requires a profound understanding of the hydrology of the region in terms of its response to floods. Additional constraints are related to the length, accuracy, and completeness of available data records, for reasons of statistical significance. An inherent limitation of this approach is, therefore, the type of hydrological variable used. Considering that river gauge networks tend to be poorly distributed and in decline, a global scale application of this method remains problematic.

As an alternative, in this study we combine the global water information provided by the PDWC2012 [5] model at high temporal (daily) and relatively coarse spatial (1 km) resolution with discontinuous but comparatively high spatial (150 m) resolution flood maps, derived from microwave remote sensing observations. The novelty of this study relies on the use of a modeled time-continuous series of flood extent or volume that covers, on a global scale and with consistent quality, a period that is adequate for enabling statistical analysis. The study site is the Severn basin (UK), a data-rich catchment that allows for a comprehensive evaluation of the proposed procedure.

A first objective of this study is to verify the existence of the pre-requisite of correlation between satellite-derived flood extent and synchronously-modeled variables, i.e. modeled flood extent and volume. Secondly, we aim to explore the possibility of using variables derived from a global scale hydrodynamic model to attribute probabilities to satellite-derived flood maps.

In this paper, we intend to highlight the complementarity of remote sensing-derived inundation maps and time-continuous modeled series for flood hazard mapping, building upon the availability for all regions of the world of a modeled time series of flood inundation map, both complete and of sufficient length for statistical analyses. The advantage of the proposed method is that it allows assigning probabilities to flood extents observed at different magnitudes. The novelty of this approach is the combination of two datasets with different spatial resolution, which is relatively coarse for a global model and higher for satellite-derived flood extents. This allows generating flood hazard maps with a resolution that is higher and arguably more accurate than what would be possible with the global model alone. This paper describes a proof-of-concept and we carefully consider the limitations of the proposed approach.

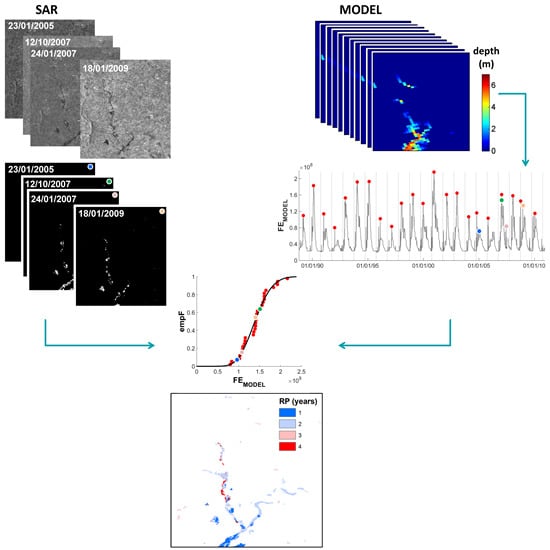
2. Method

The proposed method is based on a combination of modeled flood-related data (flood extent and volume) that are continuous in space and time with a sample of remote sensing-derived flood inundation maps (i.e., binary maps of flooded/non-flooded pixels) that are irregularly acquired.

Figure 1. Flowchart of the method.

Figure 1. Flowchart of the method.

The rationale is that the time-continuous series of modeled data, which is sufficiently long and uninterrupted, can be used to assign flood occurrence probabilities to a sample of remote sensing observations. The methodology (Figure 1) consists of the following processing steps:

(i)

to retrieve a stack of flood extent maps from all remote sensing images available over a given area of interest (AOI);

(ii)

to extract the annual maxima of a time-continuous series of flood-related data (modeled or gauged in the AOI) and to parameterize its cumulative distribution function (CDF);

(iii)

for each flood extent map, to compute the probability of the time-continuous series value at the specific satellite overpass and to attribute such probability to all flooded pixels in the flood extent map itself;

(iv)

to combine all flood maps, with associated probabilities, by selecting for each pixel the minimum probability value in the stack of flood maps, in order to obtain the final flood hazard map.

The assumption is that modeled variables and satellite derived flood extents are correlated, so that probabilities can be transferred from one series to the other.

2.1. Correlation between Time-Continuous Series and Remote Sensing Observations

A prerequisite for applying the proposed method is the existence of a significant correlation between satellite derived flood maps and the synchronously modeled variables, in our case modeled flood extent and volume.

Gauged values like discharge and water height are known to be correlated with inundation extent [37,38]. Consequently, the merit of using measured data as in Huang et al. [36] is that, when available, appropriately-selected gauged series show a strong correlation in time with flood extent. In case of a dense river network with long and complete records, an optimal selection would lead to the identification of an appropriate gauge, which is highly representative of the hydrological behavior of the region of interest. However, when dealing with large scale applications, a number of issues has to be considered. It has been estimated that 50% of the world’s rivers contain no gauges and that the number that are still active is actually declining [25,39]. Not only has the gauge to be installed in an appropriate location, but also its data record should (at least) cover the period of satellite overpasses. This condition is often not satisfied because of malfunctioning, data loss, maintenance, or damage caused by inundation. Eventually, the data record of the selected station has to be long enough and uninterrupted to allow for the subsequent statistical modeling. Another potential issue is the fact of linking a point ground measurement to a 2D inundation pattern. This means that it might be necessary to take into account flood duration and time-lag between gauge measurement and inundation.

On the other hand, the link between variables derived from a 2D grid output of a global model and satellite-observed inundation extent appears to be comparatively straightforward: the footprint of satellite-observed floods can be directly overlapped to the 2D model output, to extract the corresponding modeled values. The major limitation is the method’s sensitivity to model errors that, in specific areas, can potentially have significant adverse effects on the estimated flood hazard. For example, in a certain region of the globe the model may constantly estimate anticipated (or delayed) flood peaks. In this case, RPs attributed to satellite derived flood extents will be affected by errors due to model inaccuracies. However, Yamazaki et al. [19] showed that, for large basins (area > 8 × 10⁵ km²), the seasonal cycle of flood extent (monthly flooded areas averaged over seven years) as predicted by PDWC2012 correlates well with satellite observations, even though some discrepancies are still present. On a daily basis and on smaller basins, model results are expected to be less accurate. This motivates a preliminary evaluation of model performance, in terms of correlation between satellite-derived flood extent and modeled flood extent and volume.

Pearson’s coefficient, ρ, was used to evaluate the correlation between the observed flood extent in the AOI, here termed FE_SAR, and the synchronously modeled flood extent and surface water volume. For benchmarking purposes, we also computed ρ between FE_SAR and time-continuous series of gauged discharge. From the time-continuous series of modeled flood extent, modeled volume and gauged discharge we extracted the values at the time of each satellite observations and these values were then plotted against FE_SAR. We used the coefficient to verify the existence of a correlation that allows transferring probabilities from a hydrological series to the synchronous remote sensing observations.

Remote Sensing-Derived Flood Maps

For each SAR image, FE_SAR was estimated by multiplying the sum of all flooded cells by the cellsize.

A stack of observed flood maps can be obtained from collections of different satellites. For example Synthetic Aperture Radar (SAR) images (e.g., ENVISAT, TerraSAR-X, COSMO-SkyMed, Sentinel-1) with a resolution < 100 m are well-adapted for large scale flood mapping applications. Before the launch of Sentinel-1 mission, a major drawback of SAR missions used to be their non-systematic image acquisition mode. Several optical sensors, such as MODIS, therefore offer a collection size larger than what provided in the past by most SAR sensors. In the context of this study, the disadvantage of optical sensors is that, because of their sensitivity to cloud cover, the number of available flooding-related images could effectively be small. To deal with the issue of clouds, MODIS images are generally available as eight-day composites, while the merit of SAR satellites lies on their day and night observation capabilities, under all weather conditions, penetrating clouds which are usually present during flood events. Given the size of this study site and its floodplain (floodplain width of ~1000 m for the Severn River), we selected SAR data for their spatial resolution. Moreover, as we are interested in assigning probabilities to individual remote sensing images, we prefer working with SAR data which can be attributed to a single day of satellite overpass, rather than using image composites over more days.

To obtain a stack of binary flood inundation maps we used the automated algorithm of Giustarini et al. [12]. The algorithm combines statistical modeling of backscatter values attributed to water bodies with backscatter thresholding, region growing, and change detection, for enabling an automated, objective, and reliable flood extent extraction from SAR data [12,40,41]. The method uses as inputs two SAR backscattering images, one imaging the flood event (flood image) and another one observing the area when no flood was present (reference image). In order to make them comparable for the change detection step, the two selected images belong to the same orbital track, following the recommendations of Hostache et al. [42].

The preprocessing steps have been performed taking advantage of the Grid-Processing On Demand (G-POD) software, available through ESA facilities (http://gpod.eo.esa.int/). For each orbital track, first a reference image is selected and all other images are co-registered to this one. Subsequently, all images of a given track are calibrated and geocoded on a common cartographic system using the Shuttle Radar Topography Mission (SRTM) Digital Elevation Model (DEM), on a grid with pixel spacing equal to the nominal spatial resolution of Wide Swath acquisition mode images, 150 m.

The method assumes that the histogram of backscatter values in a flood image can be modeled as two partially overlapping histograms: one derived from the backscatter values representing “open water” in the image and the other from the backscatter values representing non-flooded areas [43]. A scaled gamma curve is fitted on the backscatter values representing “open water” and, based on this curve, a backscatter threshold parameter is determined as the value where the fitted curve and the histogram start deviating. Next, a sequence of three steps, optimized backscatter thresholding, region growing, and change detection, is applied on the flood image and the reference one.

Selecting all the pixels of the flood image with a backscatter value lower than the threshold, a preliminary flood inundation map is obtained. The same threshold is also applied to the reference image to map permanent water bodies, including also other smooth surfaces with a water surface-like radar response, such as shadow-affected areas. The preliminary flood inundation map represents the seeds for a subsequent region growing step, in which pixels in the vicinity of the seeds are included in the flood area. The regional homogeneity of the backscattering behavior helps determining a tolerance criterion that terminates the region growing process, when a given percentile of the theoretical gamma curve of “open water” pixels is exceeded. Region growing, with the same threshold value, is also applied to expand the seeds of permanent smooth surfaces obtained from the reference image, thereby providing a mask of water surface-like radar response areas that can be used to limit the region growing applied on the flood image. The region growing tolerance is optimized together with the change detection parameter by a simultaneous calibration approach [12]. The change detection step aims to remove pixels from the flood extent that do not significantly change their backscatter values with respect to a baseline of backscatter values. Its parameter is defined as the required minimum change in backscatter between reference and flood image for a pixel to be considered as flooded.

2.2. Flood Hazard

In the proposed method, outputs from a global model are used to derive a time-continuous series of modeled flood-related data (volume and flood extent) in the selected AOI. From this series, the annual maxima are extracted and used to compute non-exceedance probabilities by fitting a CDF. Later, the integration between model-derived probabilities and satellite-derived flood extent is performed. For any satellite-derived flood map, knowing its date of acquisition, we extract the synchronously-modeled variable and we compute its non-exceedance probabilities, based on the fit CDF. Such probability is then transferred to the satellite-derived flood map, attributing it to all flooded pixels in the flood extent map itself.

For comparison, following an approach similar to Huang et al. [36], we contrast the results obtained with the proposed approach against those that would have been found using in situ measured discharge as time-continuous series.

2.2.1. Flood Hazard Mapping

Extreme value theory is a branch of statistics that deals with extreme events. It aims to estimate, from a given ordered sample of a certain variable, the probability of specific events, including those that are more extreme than any previously observed. A preliminary step consists in deriving, from a given time series x, a yearly maxima series, x^max. Next, a generalized extreme value (GEV) distribution is fitted to the order-ranked series of x^max. The CDF, F, of the GEV distribution, introduced by Jenkinson [44], is used:

$$F\left(x_{max};\mu ,\sigma ,\gamma \right)= \{\begin{array}{cc}\exp \left\{-\left[1+\gamma {\left(\frac{x^{max}-\mu }{\sigma }\right)}^{-1/\gamma }\right]\right\}& 1+\gamma \frac{x^{max}-\mu }{\sigma }>0,\gamma \ne 0\\ exp\left\{-exp\left[-\frac{x^{max}-\mu }{\sigma }\right]\right\}& \gamma =0\end{array}$$

(1)

where μ, σ > 0 and γ are the location, scale, and shape parameters, respectively. The sub-families defined by γ = 0, γ > 0 and γ < 0 correspond, respectively, to the Gumbel, Frechet, and Weibull families [45]. Maximum Likelihood Estimates (MLE) [46,47] is applied to estimate GEV parameters for a given sample. For visual comparison, a sample estimate of probability, empF_i, is obtained with the plotting position of Cunnane [48]:

$$emp{F}_i= \frac{i-0.4}{N+0.2}$$

(2)

where i is the rank of the annual maxima and N the sample size.

The value of probability derived with the GEV CDF of Equation (1) represents the non-exceedance probability of a given event. The Return Period, RP, denoting the average recurrence interval over an extended period of time, is obtained from the probability F as:

$$RP= \frac{1}{1-F}$$

(3)

Once a CDF has been parameterized on the specific x^max values for the AOI of interest, the x value corresponding to the time of each remote sensing acquisition is extracted and a non-exceedance probability F is computed for it. This value is then transferred to the synchronous remote sensing-derived flood extent map: in other words, it is assumed that the spatial configuration of the flood extent has a single specific probability. This means that the computed F value is assigned to all flood pixels in the specific map.

When all the SAR-derived binary maps of the stack have been attributed an F value, each pixel is characterized by a stack of (potentially conflicting) F values. By identifying the minimum F value in the stack, we select a unique non-exceedance probability for each pixel. Hence, a regional hazard map can be generated by identifying for each pixel the lowest F value of the stack. From this non-exceedance probability map, an RP map can be computed by inverting each pixel value using Equation (3). Both maps can be considered flood hazard maps.

2.2.2. Evaluation of Results

The resulting flood hazard maps are evaluated against a reference hazard map that is computed with a numerical modeling approach. We apply scores designed to evaluate extremes [5]: the Extreme Dependency Score, EDS [49], and the Frequency Bias, FB [50].

The EDS is based on a contingency table (Table 2), which defines a, b, c, d, np, and evaluates the association between forecasted and observed rare events based on hits, a, and misses, b (not explicitly evaluating false alarms). It ranges from −1 to 1 (perfect score) with 0 indicating that there is no skill. The EDS is not sensitive to bias and, thus, needs to be complemented by the frequency bias.

$$EDS= \frac{2\text{log}\left(\frac{a+c}{np}\right)}{log\left(\frac{a}{np}\right)-1}$$

(4)

The FB measures whether the frequency of the two data sets is similar. A FB > 1 indicates that there is a positive bias (over forecasting) of the data set computed in this study in comparison to the reference data set (and vice versa). It ranges from 0 to ∞, with 1 indicating a perfect score.

$$FB= \frac{a+b}{a+c}$$

(5)

Table 2. Contingency table (np = a + b + c + d).

		Reference Hazard Map
		Flooded	Non-flooded
Hazard map	Flooded	a	b
to be validated	Non-flooded	c	d

Table 2. Contingency table (np = a + b + c + d).

		Reference Hazard Map
		Flooded	Non-flooded
Hazard map	Flooded	a	b
to be validated	Non-flooded	c	d

3. Study Site

The floodplain area of the Severn River in the UK has been affected by several flood events in recent years. A preliminary analysis revealed that a relatively high number of floods were observed by ENVISAT in that region.

The AOI of our study covers an extent of [51.9, 52.4] degrees of latitude and [−2.4, −1.9] degrees of longitude, as displayed in Figure 2. It has been chosen for two main reasons: (i) it covers an alluvial plain that is frequently affected by floods in the region, and (ii) a LISFLOOD-FP hydraulic model is available together with long records of in situ measured river discharge. The latter can be used to compute a reference hazard map with a traditional approach based on numerical modeling. This region is a data-rich environment, where model inputs, i.e. peak discharges of selected RPs, can be derived from statistical analysis of long discharge records.

Figure 2. Study site of the River Severn, with its basin (in red) closed at the gauging station of Haw Bridge: the AOI is given by the rectangular box and the dots represent available gauging stations.

Figure 2. Study site of the River Severn, with its basin (in red) closed at the gauging station of Haw Bridge: the AOI is given by the rectangular box and the dots represent available gauging stations.

The AOI covers an area of ~1700 km², extending over the floodplain comprised between the stations of Bewdley, Evesham, Kightsford Bridge, Kidderminster, and Haw Bridge. This intermediate catchment is composed by the sub-basin of the Avon and the sub-basin of the Severn. The Avon flows in from the East and is equipped with a gauging station inside the AOI at Bredon. The part of the Severn catchment that is located before the confluence with the Avon, represents the western side of the inter-basin inside the AOI and is gauged at Saxons Lode and at Upton on Severn. After the confluence, gauges are positioned at Deerhust and at Haw Bridge.

The region is a rural environment, with the only major town being Tewkesbury, located on the east side at the confluence of Severn and Avon. In terms of land cover, half of the basin at Haw Bridge is characterized by grassland, a third occupied by arable land and the remaining portion subdivided in woodland and montane habitats, with only a minor portion occupied by urban areas. The maximum altitudes are in the western part of the catchment, which is also characterized by very low permeability. The northern portion is defined as highly permeable, while the eastern one shows mixed to very low permeability, as well as the region included in the AOI. The climate of the region shows a small gradient in measured rainfall, with the highest precipitation located on the west, diminishing towards the east: in the selected AOI, little spatial variation of rainfall has been observed.

4. Datasets

4.1. Satellite-Derived Flood Maps

For the given AOI, we retrieved a dataset composed of 389 ENVISAT ASAR Wide Swath mode images characterized by a spatial resolution of 150 m, acquired from different orbital tracks in the period 2005–2012: 19 of these images observed flood events. Most flood maps are available for the years 2007 and 2008, which were characterized by high-magnitude flood events. It can be noted that no floods were observed in 2005, 2006, and 2011. From streamflow records it is known that these years were very dry periods.

As the information provided by PDWC2012 is available on a daily basis (attributed at midday of each day), for those days with more than one SAR observation, we selected only the map whose time of acquisition is closer to midday. In conclusion, out of the 19 images of floods, we eventually retained 12 images, for a total number of 12 days where inundation was observed and FE_SAR was computed. They include the 2007 summer flood, one of the highest events observed by satellite on the Severn.

4.2. Time-Continuous Series

The length of a series, i.e. the number of samples, determines the reliability and robustness of any statistic estimators. It has to be noted that series of 30 years or less are rather common in operational hydrology, a field where only rarely more than 40 years of recorded data are available for statistical analysis [51]. In our method, the time-continuous series is derived from a global model that provides as output 30 years of daily maps of water depth. Only for comparison, we also test the proposed method using gauged data as time-continuous series, following an approach similar to Huang et al. [36].

Time series of in situ measurements are typically characterized by random errors, while time series based on simulations may show systematic biases. For this reason, checking the existence of a good match between simulated and satellite-observed values is an essential prerequisite.

4.2.1. PDWC2012 Model-Derived Variables

PDWC2012 is the European Centre for Medium Range Weather Forecasts (ECMWF) land surface model [5], which is coupled to ERA-Interim reanalysis meteorological forcing data and whose resultant runoff is passed to a river routing algorithm that simulates floodplains and flood flow across the global land area. It has a daily temporal resolution and a relatively coarse spatial resolution of 1 km. Its output consists of simulated daily water depth maps [m] ranging from 1980 to 2010, for a total of 30 complete water years. The series of modeled flood extent, FE_PDWC2012, inside the AOI is obtained by multiplying the cell size with the number of cells having depth values greater than zero. Modeled volume, V_PDWC2012, represents the surface water storage within the AOI and is computed by multiplying the cell size with the sum of water depth values.

4.2.2. Gauged Daily Flow (GDF)

GDF data is provided by the National River Flow Archive (NRFA) (http://www.ceh.ac.uk/data/nrfa/data). The periods of record for the different gauges in the AOI are given in Table 3:

Table 3. Available stations and periods of record.

	Period of Record
Bewdley	1921–2013
Knightsford Bridge	1970–2013
Kidderminster Callows Lane	1953–2013
Evesham	1936–2013
Haw Bridge	1971–2013
Saxons Lode	1970–2013
Upton on Severn	1955–1970
Deerhust	2001–2012 (of which some years incomplete)
Bredon	1988–2011 (of which 7 years are missing and some incomplete)

Table 3. Available stations and periods of record.

	Period of Record
Bewdley	1921–2013
Knightsford Bridge	1970–2013
Kidderminster Callows Lane	1953–2013
Evesham	1936–2013
Haw Bridge	1971–2013
Saxons Lode	1970–2013
Upton on Severn	1955–1970
Deerhust	2001–2012 (of which some years incomplete)
Bredon	1988–2011 (of which 7 years are missing and some incomplete)

Of all the stations listed in Table 3, four of them are located inside the AOI and are good candidates to check for their representativeness of flooding in the region. Recorded series at Deerhust and at Bredon are incomplete and too short for statistical analysis of extremes, in which only complete years are considered to extract yearly maxima. On the other hand, both Saxons Lode and Upton on Severn present complete and sufficiently long series but they are affected by bypassing for the highest flows. Based on analysis of the AOI river network, Haw Bridge and Deerhust are expected to be the most representative stations for the inundation of the region. The four stations inside the AOI and the one located at Haw Bridge were tested for correlation with satellite derived flood extent.

It has to be noted that during extreme events, gauging stations are subject to failure: stations may be damaged or measured water levels may be outside the range of values for which a rating curve has been estimated. On the other hand, the events we are interested in are exactly those that cause overbank inundation, for which gauged data are often provided with the highest uncertainty. In particular, for the summer 2007 flood, one of the highest events observed on the Severn, discharge values at Haw Bridge do not derive from in situ measurements but are modeled discharge data reconstructed with hydraulic modeling. For the same event, discharge provided at Bredon is labeled as “suspect”, while gauged values at Saxons Lode are flagged as “estimated”. Another problem is that data at Deerhust were not available for this event. Therefore, the 2007 flood was excluded from the analysis.

4.3. Reference Hazard Map

A reference hazard map (Figure 3) has been computed with a traditional approach, based on numerical modeling. The LISFLOOD-FP model [52,53] is a two-dimensional hydrodynamic model specifically designed to simulate floodplain inundation in a computationally efficient manner. It has been set-up for the AOI, using as inputs peak discharge of selected RPs at Bewdley on the Severn and at Evesham on the Avon. These are the main tributaries to the AOI. A Gumbel distribution has been hypothesized as statistical distribution of the annual maxima discharge of the two stations by applying the maximum likelihood method.

Figure 3. Reference hazard map computed with LISFLOOD-FP inside the AOI.

Figure 3. Reference hazard map computed with LISFLOOD-FP inside the AOI.

Synthetic hydrographs having a peak discharge of selected RPs, ranging from 2 to ~300 years, were routed though the model to derive the maximum flood extent for each set of inputs of given RP.

5. Results

5.1. Analysis of Correlation

Here we display results in terms of correlation between hydrological series derived from PDWC2012, FE_PDWC2012 and V_PDWC2012, and flood extent, FE_SAR, as obtained from remote sensing. In parallel, we analyze the correlation between available gauged series in the AOI and FE_SAR.

The selected 12 SAR images of floods were provided as input to the algorithm of Giustarini et al. [12] to obtain binary maps of flood extents over the selected AOI. Figure 4 displays in panel (a) an example of such a binary map, together with an example of a depth map in panel (b) as provided for the same day by PDWC2012. It is important to highlight the difference of one order of magnitude between model (1 km) and image (150 m) resolution. More details of the spatial inundation pattern are visible in the selected satellite image, whereas only the major body of the flood is captured by the model results. Such heterogeneity in the spatial scale introduces discrepancies and inaccuracies in the computation of correlation between the two datasets. On the other hand, this comparison also shows that merging model results and remote sensing-derived observations allows generating flood hazard maps that have a resolution that is higher and arguably more accurate than what would be possible with the global model alone.

Figure 4. Example of (a) flood binary map and (b) corresponding daily PDWC2012 depth map, for the selected AOI.

Figure 4. Example of (a) flood binary map and (b) corresponding daily PDWC2012 depth map, for the selected AOI.

As already mentioned, the summer 2007 flood was excluded from this analysis, due to malfunctioning of several gauges. The flood map of this event was consequently omitted from the retained sample of 12 SAR images of floods. For the remaining 11 SAR observations, Figure 5 displays the correlation between observed flood extent inside the AOI and hydrological variables at the time of satellite overpasses. As the units of variables are different, they have been rendered dimensionless, each with respect to its maximum value.

Figure 5. Correlation between FE_SAR and hydrological variables in the rectangular AOI: (a) GDF at Haw Bridge; (b) GDF at Deerhust; (c) GDF at Saxons Lode; (d) GDF at Bredon; (e) FE_PDWC2012; (f) V_PDWC2012.

Figure 5. Correlation between FE_SAR and hydrological variables in the rectangular AOI: (a) GDF at Haw Bridge; (b) GDF at Deerhust; (c) GDF at Saxons Lode; (d) GDF at Bredon; (e) FE_PDWC2012; (f) V_PDWC2012.

Concerning the time series of discharge measurements, we selected from the ensemble of available stations in the AOI those that are hypothesized to be representative of flood in the AOI. Haw Bridge and Deerhust, which are positioned on the main river downstream of the confluence between Severn and Avon, are selected and tested for correlation. A very high correlation value, ρ GDF_DE-FE_SAR, is found for the station at Haw Bridge (panel a), which is also characterized by a long record of 41 water years. The gauge at Deerhust (panel b), located a few kilometers upstream of Haw Bridge and closer to the confluence, also presents a good correlation, ρ GDF_DE-FE_SAR. However, it has to be noted that the correlation could only be computed for five images, as this station record shows several episodes of missing data. Also, data availability at Deerhust covers only a period of ~10 years, which extends over the years of satellite observations, allowing assessing its representativeness with respect to FE_SAR, but that is not numerous enough for statistical analysis. Other stations, i.e., Saxons Lode (panel c) and Bredon (panel d), located on the two main tributaries, have been also tested for correlation with flood extent. The observed ρ values were predictably lower, as it was expected due to the fact that the two stations are located on the Severn and Avon sub-basins, respectively, and therefore are not representative of the total AOI. Even when dealing with a data-rich region, the choice of an appropriate gauging station is a sensitive issue: malfunctioning and shortness of the record period may hamper the use of a gauged time-continuous series in the proposed procedure.

Considering modeled flood extent (panel e) and volume (panel f), the correlation with FE_SAR is lower than what obtained for gauged data at Haw Bridge and Deerhust. This is arguably due to the fact that PDWC2012 is a global model that cannot be expected to have flawless performance on a local level and on a daily basis. FE_PDWC2012 has a higher correlation with flood observations than V_PDWC2012, as could be expected given the quantities that they represent. This may indicate a better capacity of PDWC2012 in terms of reproducing variations in flood extent than in storage volume. Moreover, it has to be considered that a variable like volume is strongly affected by the local topography. Therefore, we chose to consider FE_PDWC2012 for testing the approach. The results will be contrasted to those obtained using the discharge data at Haw Bridge, having the highest ρ value and a sufficiently long data record.

5.2. Flood Hazard Mapping

Considering the rectangular AOI, two hazard maps have been computed: one using a time-continuous series GDF at Haw Bridge, here termed HM_GDF, the second one using FE_PDWC2012, here named HM_FE.

For the two series, yearly maxima have been extracted (see red dots in Figure 6) for each water year and a GEV CDF has been fitted on them through MLE, obtaining the parameters reported in Figure 6. For a visual comparison, the plotting position of x^max is displayed together with the CDF, its parameters and corresponding 95% confidence intervals (in brackets). The x values at the dates of the satellite overpasses (blue dots) have then been used to extract from the CDF an F and an RP value that can be transferred to each corresponding binary flood map, as reported in Table 4.

Figure 6. Yearly maxima (red dots) and CDF fit; the values of the continuous series at the times of satellite overpasses are also shown (blue dots).

Figure 6. Yearly maxima (red dots) and CDF fit; the values of the continuous series at the times of satellite overpasses are also shown (blue dots).

The scatter plot of RPs for the 11 events (Figure 7) shows that there are some differences between return periods attributed to each flood map, using as time-continuous series either FE_SAR or GDF at Haw Bridge, respectively. As can be expected, differences are higher with higher RPs. However, it has to be noted that in one case the time-continuous series derives from a global-scale 2D model (originally with a grid size of 25 km and re-projected to 1 km), while in the other, it comes from point gauged measurements. Considering this significant difference in scale, the trend observed in Figure 7 can be regarded as a sufficient agreement in terms of resulting RP.

Table 4. RPs attributed to the different SAR-derived flood extent.

	RP (Years)
dates	FEPDWC2012	GDF Haw Bridge
26 January 2007 10:20:58	2.1	1.0
05 March 2007 10:27:41	1.8	1.9
08 March 2007 10:34:40	1.8	2.9
10 December 2007 21:53:19	1.0	1.1
14 January 2008 21:52:34	1.0	1.8
17 January 2008 21:55:15	2.0	3.8
24 January 2008 10:12:18	3.7	2.4
12 September 2008 21:46:50	1.0	1.0
15 September 2008 10:27:39	1.0	1.0
12 February 2009 10:12:13	1.2	1.0
18 January 2010 10:30:31	1.1	1.8

Table 4. RPs attributed to the different SAR-derived flood extent.

	RP (Years)
dates	FEPDWC2012	GDF Haw Bridge
26 January 2007 10:20:58	2.1	1.0
05 March 2007 10:27:41	1.8	1.9
08 March 2007 10:34:40	1.8	2.9
10 December 2007 21:53:19	1.0	1.1
14 January 2008 21:52:34	1.0	1.8
17 January 2008 21:55:15	2.0	3.8
24 January 2008 10:12:18	3.7	2.4
12 September 2008 21:46:50	1.0	1.0
15 September 2008 10:27:39	1.0	1.0
12 February 2009 10:12:13	1.2	1.0
18 January 2010 10:30:31	1.1	1.8

Figure 7. Scatter plots of RPs obtained using as time continuous series FE_PDWC2012 and GDF at Haw Bridge.

Figure 7. Scatter plots of RPs obtained using as time continuous series FE_PDWC2012 and GDF at Haw Bridge.

Table 4 and Figure 7 highlight the differences in terms of RPs, considering every flood map as independent from the others of the stack (see step iii of the methodology). In other words, all flooded pixels in a given flood map are attributed the same RP value obtained for the synchronous value of the time-continuous series. This means that at this stage, a given pixel is characterized by a stack of (potentially conflicting) F values. Subsequently, in step (iv) all flood maps, with associated probabilities, are combined to obtain a single flood hazard map. For each pixel we identify the minimum F value in the stack, thereby attributing a unique F and a corresponding unique RP to each pixel, in order to generate the flood hazard map. Figure 8 provides a comparison between the two flood hazard maps created using the two time series (i.e., HM_FE and HM_GDF).

Both flood hazard maps present RPs ranging from one to four years. For a given flood extent, HM_FE tends to attribute a somewhat higher return period than HM_GDF, particularly in the central portion of the AOI. However, visual inspection shows that the spatial pattern and the trend of increasing RPs are similar for both maps.

Figure 8. Hazard maps: (a) HM_FE with probabilities estimated through FE_PDWC2012 and (b) HM_GDF with probabilities estimated through GDF at Haw Bridge.

Figure 8. Hazard maps: (a) HM_FE with probabilities estimated through FE_PDWC2012 and (b) HM_GDF with probabilities estimated through GDF at Haw Bridge.

5.3. Evaluation

Both hazard maps, HM_FE and HM_GDF, have been quantitatively evaluated using as reference the hazard map obtained with the LISFLOOD-FP model. However, it has to be noted that the maximum RP of the benchmark map (~300 years) is higher than those in the two hazard maps generated in this study. In fact, in any modeling approach, synthetically-generated hydrographs are used to estimate the extent of flooding for very rare and potentially never observed events.

The skill scores of Figure 9 describe how HM_FE and HM_GDF compare against the LISFLOOD-FP reference data set. The EDS is always above 0.5, thereby indicating skill at all RPs, with a trend to improve with increasing RPs. The FB is above 1 for all RPs for both hazard maps: this indicates that, for any tested RP lower than 10 years, they both have a higher number of flooded cells than the reference LISFLOOD-FP hazard map. This means that both maps overestimate RPs with respect to the LISFLOOD-FP hazard map.

Figure 9. Scores of RPs for (a) HM_FE and (b) HM_GDF compared against the LISFLOOD-FP reference.

Figure 9. Scores of RPs for (a) HM_FE and (b) HM_GDF compared against the LISFLOOD-FP reference.

The analysis has then been extended by considering HM_FE as map to be evaluated and assuming HM_GDF to be the reference map (see Table 2). The skill scores of Figure 10 confirm the similarity between the maps, as expected from the results shown in Figure 8. In particular, EDS has a value close to its optimum: this indicates skill for all considered RPs and a trend that shows improvements with increasing RPs. FB indicates a slight overestimation of HM_FE with respect to HM_GDF.

Figure 10. Score indices of RPs for HM_FE compared against HM_GDF as reference.

Figure 10. Score indices of RPs for HM_FE compared against HM_GDF as reference.

6. Discussion

6.1. Analysis of Correlation

Variables derived from a global model, both in terms of flood extent and volume, where found to be sufficiently correlated with the synchronous SAR-observed flood extent. As can be expected, their correlations are slightly lower than the correlation that can be found between a carefully selected gauging station and remotely-sensed inundation extents. This outcome is due to a combination of factors. On the one hand, PDWC2012 is a cascade of process-based models, with a variety of sources of uncertainty. In particular, input data, the use of low-resolution DEM, the lack of bathymetry datasets at the global scale, and the complexity in spatial connections between the main channel and floodplain introduce difficulties in modeling accuracy and make so that hydrodynamic simulations at large scale remain highly uncertain. PDWC2012 models inundation on a global scale and at relatively coarse resolution and may, thus, fail to accurately simulate a river basin’s local response in certain areas of the globe. On the other hand, the selection of a gauging station is guided by the understanding of the hydrological behavior of the specific region of interest, which explains the higher correlation with the inundation pattern [36].

Before attempting to map flood hazard using the proposed approach it is, thus, critical to evaluate if, for the region of interest, PDWC2012 variables are sufficiently well-correlated to the sequence of observed inundation extents. Only if this is the case, statistics inferred from model results can be transferred to satellite-derived flood maps. When the correlation is not significant, it is clearly not recommended to apply this method for flood hazard mapping. However, one could argue that this verification is helpful to detect areas of the globe where PDWC2012 has a lower performance and where, as a consequence, structural improvements or local recalibration of model parameters may be considered. The approach introduced in this study has the advantage that it benefits from continuous model developments and recalibration of certain areas of the globe will improve model predictions in terms of both flood extent and volume.

6.2. Flood Hazard Mapping

The flood hazard map obtained with the proposed method, HM_FE, has been evaluated against a reference hazard map, computed with a traditional hydraulic modeling-based approach. Some discrepancies have been observed: in particular, HM_FE tends to provide a lower RP than the reference map. The same trend has been found when computing a flood hazard map, HM_GDF, using an approach similar to the one of Huang et al. [36]. An inter-comparison between HM_FE and HM_GDF shows that differences between the two maps are rather insignificant. This is encouraging in the sense that not only is the global model PDWC2012 sufficiently correlated with observations, but it can be also used for flood hazard mapping, obtaining similar results to those found with a carefully-selected gauge station.

Concerning the consistent underestimation of RPs observed in both HM_FE and HM_GDF with respect to the reference map, a visual inspection reveals that, according to both GDF at Haw Bridge and PDWC2012 simulations, the period 2005–2010 covered by the available ENVISAT data was a relatively dry one. Gauged and simulated values were below those of some of the previous years, e.g., 1990 or 2000. Hence, even under the unlikely scenario where all floods of the period 2005–2010 had been observed by a satellite at peak discharge, the remote sensing-based approach introduced in this study would have not generated any flood hazard map exceeding five years RP.

Finally, it has to be mentioned that the flood extents of the reference map (Figure 3) have been attributed the RP of the design flood hydrographs that were used as inputs of the hydrodynamic model. It is well known that this assumption is not always valid, particularly in situations where long river reaches are considered and long travel times and possible interactions between different tributaries play a significant role. In this paper we adopt a slightly different approach that does not require the computation of specific design flood hydrographs, but rather directly considers a long time series of modeled flood extents (or volumes). As a consequence, we do not rely on the existence of an unambiguous relationship between a set of discharge inputs and the model-derived flood extent. We propose to attribute to remotely-observed flood inundations the RP of the synchronously-modeled value, provided that a strong correlation exists between model results and observations. This prerequisite can be verified a priori, as shown above, before proceeding to flood hazard mapping. Following these considerations, in the comparison between Figure 3 and Figure 8a, similar flood extents may have been attributed rather different RPs due to the inherent differences in the methodologies that were applied to compute them.

In principle, the uncertainties associated with the fitted distribution parameters could also be considered to estimate their impact on the generated flood hazard maps.

6.3. Advantages and Limitations of the Proposed Method

The merit of the proposed method lies in the use of flood-related variables, derived from the 2D output of a global model, to attribute probabilities to satellite derived maps. It transfers exceedance probabilities inferred from the modeled series to a sample of flood extent maps, obtained from SAR images and having a resolution higher than that of the global model. The novelty of this study is that, combining two datasets of different spatial and temporal resolution, it allows generating a flood hazard map with a resolution that is higher than what would be possible with a global model alone.

A global model like the one used in this study [5] provides for all regions of the world a continuous series of sufficient length for statistical analysis. To check its representativeness with respect to satellite-observed floods, it is necessary to carry out a preliminary analysis of correlation between modeled and remotely-sensed variables, before applying the proposed method. A model like PDWC2012 provides globally-consistent maps, meaning that all grid point values have been derived in the same way. According to Pappenberger et al. [5], the quality and behavior of the underlying meteorological forcing is clearly dependent on the local geography. While the quality of the simulations may, thus, vary in space and time, the global model provides a homogeneous framework for carrying out flood hazard studies at a large scale. A major limitation of the proposed method is its dependency on the model accuracy. The use of a modeled variable implies that any error in the modeled data is transferred to the final hazard map. Once more, scatter plots like those in Figure 3 help evaluating if, for the region of interest, PDWC2012 is correlated to the observed inundations and, if, consequently, its statistics can be transferred to the flood maps. It is important to bear in mind that, when available, in situ discharge measurements will most probably offer the highest correlation with satellite derived inundations.

Concerning remote sensing inputs, we currently use ENVISAT images, which we selected for their relatively high spatial resolution and the size of the collection. Our aim is to assign probabilities to all individual observed inundations. On the other hand, Huang et al. [36] were interested in mapping the yearly maximum flood extent and assumed that this is identified as the extent observed at the time of the annual peak recorded in discharge measurements. For this, they used aggregated MODIS images, covering a period of 56 days around the annual peak, so that each peak registered at a gauge can be related to a satellite image. Regarding the method we propose in this paper, it has the merit of being flexible in terms of remote sensing inputs: any type of satellite-derived binary map can be included and a combination of acquisitions from different sensors, like Sentinel-1, COSMO-SkyMed, TerraSAR-X, etc. can be easily envisaged. The same flexibility applies to the hydrodynamic model used in the method. Moreover, other than a rectangular AOI, as used in this study, different sizes and shapes can be envisaged to discretize the landscape and define the region of interest.

A limitation that our method shares with the one of Huang et al. [36] is the fact that the highest F value that can be mapped is the one that was actually observed by a satellite. It is, thus, not possible to provide an estimate of the extent of flooding with F values higher than the maximum observed. This is a fundamental difference with respect to any modeling approach where synthetically-generated hydrographs that were never observed in the past can be used to estimate the extent of flooding for very rare (and never observed) events.

7. Conclusions

A new method for estimating flood hazard combining multi-year remote sensing observations and hydrodynamic modeling was presented. It strives at combining the respective strengths of global flood inundation modeling (i.e., time and space continuity) and microwave remote sensing (i.e., higher spatial resolutions). The approach aims to reduce the respective weaknesses, such as coarse spatial resolution and high uncertainty (in the case of global numerical models) and discontinuous data acquisitions over comparatively short time periods (in the case of microwave remote sensing observations). One of the main problems of remote sensing-based flood hazard analysis is that it is impossible to correctly estimate non-exceedance probabilities from a discontinuous sample of remote sensing observations. The proposed method allows linking probabilities estimated from a global hydrological model to individual remote sensing-derived flood extent maps.

Variables derived from a global model, either in terms of flood extent or volume, were found to be sufficiently correlated with SAR-observed flood extents. Having verified that modeled variables and satellite derived flood extents are correlated, probabilities were transferred from the time-continuous modeled series to the discontinuous sequence of maps. All inundation maps, with their associated non-exceedance probabilities, were combined to obtain a single flood hazard map. Evaluation of this map with respect to a reference hazard map, computed with a pure numerical modeling-based approach, highlights some discrepancies. However, it was found that the proposed approach leads to similar results, either using, as time-series, model results or in situ measurements. This is encouraging in the sense that the proposed approach can potentially be applied to any point in the world, provided that a sufficient number of remote sensing images are available and that a correlation is present between global model simulation and satellite observations. However, it has to be noted that this work is a first proof-of-concept study, in a small, yet well instrumented, area of in interest, and that its representativeness for future world-wide applications still has to be tested.

While this approach has the interesting merit of being independent from gauged data for deriving statistics, our analysis also shows that further improvements are still required in order to generate a reliable and useful flood hazard map. First, it is of paramount importance to continue improving global flood inundation models, either the PDWC2012 model used in this study or any other hydrodynamic model adopted for the proposed method. Errors in the model are directly transferred to the derived hazard map, with potentially significant adverse effects. Second, it is of similar importance to continue increasing the representativeness and the length of the time period covered by remote sensing observations. Especially in regions of the world where floods only last between some hours and a couple of days, it is very important that the (rare) floods are observed by satellites close to their peaks in order to estimate flood hazard. The problem of representativeness can be addressed today by combining data from several space missions, i.e., the recent Sentinel-1 and COSMO-SkyMed constellations. Flood hazard can only be estimated from remote sensing observations if images over many years are being considered. As long as this is not the case, methods like the one presented in this paper help to partially address the issue of short time periods covered by remote sensing observations.