An Optimal Sampling Design for Observing and Validating Long-Term Leaf Area Index with Temporal Variations in Spatial Heterogeneities
Abstract
:1. Introduction
2. Methodology
2.1. Sampling Strategy Based on Multi-Temporal a Priori Knowledge
- (1)
- Acquire multi-temporal VI images and the vegetation classification map from historical a priori knowledge.
- (2)
- Randomly select a group of n ESUs from all the fine-resolution pixels of the entire site.
- (3)
- Calculate the OF for the group of ESUs based on Equations (1)–(5).
- (4)
- Start the simulated annealing algorithm to search for the optimal group of ESUs.
- (5)
- Perform the change of an ESU in the group.
- (6)
- Repeat steps (3)–(5) until the OF value falls beyond the given stopping criterion OF < 0.01, or the defined maximum number of iterations 10,000 is reached.
2.2. Sampling Strategy Evaluation Procedure

3. Study Sites and Data Processing
3.1. Data Acquired and Processed for the Sampling Strategy Evaluation

| Class Type | N | Cab (μg/cm2) | Cw (cm) | Cm (g/cm2) | ALA (°) |
|---|---|---|---|---|---|
| Corn | 2.275 | 31.5 | 0.0075 | 0.0058 | 63.24 |
| Wheat | 1.518 | 53.2 | 0.0131 | 0.0037 | 57.3 |
| Rape | 2.656 | 44.8 | 0.0003 | 0.0066 | 26.76 |
3.2. Data Acquired and Processed for the Sampling Strategy Application

4. Results and Discussion
4.1. Evaluation of the ESUs Spreading in the Multi-Temporal Feature Space


4.2. Evaluation of the ESUs Spreading in the Geographical Space


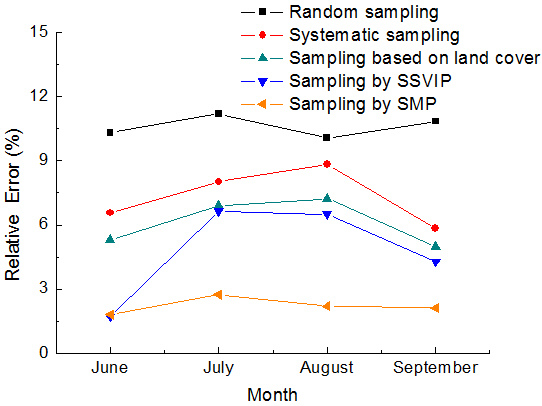
4.3. Accuracy Analysis of the LAI Reference Maps

4.4. Application to LAINet Observations at Huailai Site




| LAI Product | R2 | RMSE | Bias | Relative Uncertainty |
|---|---|---|---|---|
| MOD15A2 | 0.78 | 0.21 | 0.10 | 7.6% |
| MYD15A2 | 0.58 | 0.50 | −0.36 | 18.3% |
| MCD15A2 | 0.82 | 0.20 | −0.07 | 7.4% |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, J.M.; Black, T. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Stenberg, P. Correcting LAI-2000 estimates for the clumping of needles in shoots of conifers. Agric. For. Meteorol. 1996, 79, 1–8. [Google Scholar] [CrossRef]
- Bonan, G.B. Land-atmosphere interactions for climate system models: Coupling biophysical, biogeochemical, and ecosystem dynamical processes. Remote Sens. Environ. 1995, 51, 57–73. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Martonchik, J.; Myneni, R.; Diner, D.; Running, S. Synergistic algorithm for estimating vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from MODIS and MISR data. J. Geophys. Res. Atmos. 1998, 103, 32257–32275. [Google Scholar] [CrossRef]
- Bacour, C.; Baret, F.; Beal, D.; Weiss, M.; Pavageau, K. Neural network estimation of LAI, FAPAR, FCOVER and LAIXCAB, from top of canopy MERIS reflectance data: Principles and validation. Remote Sens. Environ. 2006, 105, 313–325. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B. Global vegetation phenology from Moderate Resolution Imaging Spectroradiometer (MODIS): Evaluation of global patterns and comparison with in situ measurements. J. Geophys. Res. Biogeosci. 2006, 111, G04017. [Google Scholar]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Niño, F.; Weiss, M.; Samain, O.; et al. LAI, FAPAR and FCOVER cyclopes global products derived from vegetation: Part 1: Principles of the algorithm. Remote Sens. Environ. 2007, 110, 275–286. [Google Scholar]
- Ganguly, S.; Samanta, A.; Schull, M.A.; Shabanov, N.V.; Milesi, C.; Nemani, R.R.; Knyazikhin, Y.; Myneni, R.B. Generating vegetation leaf area index earth system data record from multiple sensors. Part 2: Implementation, analysis and validation. Remote Sens. Environ. 2008, 112, 4318–4332. [Google Scholar]
- Ganguly, S.; Schull, M.A.; Samanta, A.; Shabanov, N.V.; Milesi, C.; Nemani, R.R.; Knyazikhin, Y.; Myneni, R.B. Generating vegetation leaf area index earth system data record from multiple sensors. Part 1: Theory. Remote Sens. Environ. 2008, 112, 4333–4343. [Google Scholar] [CrossRef]
- Chen, J.M.; Pavlic, G.; Brown, L.; Cihlar, J.; Leblanc, S.; White, H.; Hall, R.; Peddle, D.; King, D.; Trofymow, J.; et al. Derivation and validation of Canada-wide coarse-resolution leaf area index maps using high-resolution satellite imagery and ground measurements. Remote Sens. Environ. 2002, 80, 165–184. [Google Scholar]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y. Heihe watershed allied telemetry experimental research (Hiwater): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Li, Z.; Ma, M.; Wang, J.; Xiao, Q.; Liu, Q.; Che, T.; Chen, E.; Yan, G. Watershed allied telemetry experimental research. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Tian, Y.; Woodcock, C.E.; Wang, Y.; Privette, J.L.; Shabanov, N.V.; Zhou, L.; Zhang, Y.; Buermann, W.; Dong, J.; Veikkanen, B.; et al. Multiscale analysis and validation of the MODIS LAI product: Ii. Sampling strategy. Remote Sens. Environ. 2002, 83, 431–441. [Google Scholar]
- Morisette, J.T.; Baret, F.; Privette, J.L.; Myneni, R.B.; Nickeson, J.E.; Garrigues, S.; Shabanov, N.V.; Weiss, M.; Fernandes, R.A.; Leblanc, S.G.; et al. Validation of global moderate-resolution LAI products: A framework proposed within the CEOS land product validation subgroup. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1804–1817. [Google Scholar]
- Zeng, Y.L.; Li, J.; Liu, Q.H. Global LAI ground validation dataset and product validation framework: A review. Adv. Earth Sci. 2012, 27, 165–174. [Google Scholar]
- Whitford, K.; Colquhoun, I.; Lang, A.; Harper, B. Measuring leaf area index in a sparse eucalypt forest: A comparison of estimates from direct measurement, hemispherical photography, sunlight transmittance and Allometric regression. Agric. For. Meteorol. 1995, 74, 237–249. [Google Scholar] [CrossRef]
- Nackaerts, K.; Coppin, P.; Muys, B.; Hermy, M. Sampling methodology for LAI measurements with LAI-2000 in small forest stands. Agric. For. Meteorol. 2000, 101, 247–250. [Google Scholar] [CrossRef]
- Law, B.; Van Tuyl, S.; Cescatti, A.; Baldocchi, D. Estimation of leaf area index in open-canopy ponderosa pine forests at different successional stages and management regimes in Oregon. Agric. For. Meteorol. 2001, 108, 1–14. [Google Scholar] [CrossRef]
- Buermann, W.; Helmlinger, M. Safari 2000 LAI and FPAR Measurements at SUA Pan, Botswana, Dry Season 2000. Available online: http://daac.ornl.gov//S2K/safari.shtml (accessed on 26 December 2004).
- Majasalmi, T.; Rautiainen, M.; Stenberg, P.; Rita, H. Optimizing the sampling scheme for LAI-2000 measurements in a boreal forest. Agric. For. Meteorol. 2012, 154, 38–43. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. A conditioned Latin hypercube method for sampling in the presence of ancillary information. Comput. Geosci. 2006, 32, 1378–1388. [Google Scholar] [CrossRef]
- Mulder, V.; de Bruin, S.; Schaepman, M. Representing major soil variability at regional scale by constrained Latin hypercube sampling of remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 301–310. [Google Scholar] [CrossRef]
- Yang, L.; Zhu, A.X.; Qi, F.; Qin, C.Z.; Li, B.; Pei, T. An integrative hierarchical stepwise sampling strategy for spatial sampling and its application in digital soil mapping. Int. J. Geogr. Inf. Sci. 2013, 27, 1–23. [Google Scholar] [CrossRef]
- Zeng, Y.L.; Li, J.; Liu, Q.H.; Li, L.H.; Xu, B.D.; Yin, G.F.; Peng, J.J. A sampling strategy for remotely sensed LAI product validation over heterogeneous land surface. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3128–3142. [Google Scholar] [CrossRef]
- Baret, F.; Weiss, M.; Allard, D.; Garrigues, S.; Leroy, M.; Jeanjean, H.; Fernandes, R.; Myneni, R.; Privette, J.; Morisette, J.; et al. Valeri: A Network of Sites and a Methodology for the Validation of Medium Spatial Resolution Land Satellite Products. Available online: http://w3.avignon.inra.fr/valeri/ (accessed on 28 December 2005).
- Martinez, B.; García-Haro, F.; Camacho-de Coca, F. Derivation of high-resolution leaf area index maps in support of validation activities: Application to the cropland Barrax site. Agric. For. Meteorol. 2009, 149, 130–145. [Google Scholar] [CrossRef]
- Wang, Y.; Woodcock, C.E.; Buermann, W.; Stenberg, P.; Voipio, P.; Smolander, H.; Häme, T.; Tian, Y.; Hu, J.; Knyazikhin, Y. Evaluation of the MODIS LAI algorithm at a coniferous forest site in Finland. Remote Sens. Environ. 2004, 91, 114–127. [Google Scholar] [CrossRef]
- Claverie, M.; Vermote, E.F.; Weiss, M.; Baret, F.; Hagolle, O.; Demarez, V. Validation of coarse spatial resolution LAI and FAPAR time series over cropland in southwest France. Remote Sens. Environ. 2013, 139, 216–230. [Google Scholar] [CrossRef]
- Heiskanen, J.; Rautiainen, M.; Stenberg, P.; Mõttus, M.; Vesanto, V.H.; Korhonen, L.; Majasalmi, T. Seasonal variation in MODIS LAI for a boreal forest area in Finland. Remote Sens. Environ. 2012, 126, 104–115. [Google Scholar] [CrossRef]
- Ryu, Y.; Verfaillie, J.; Macfarlane, C.; Kobayashi, H.; Sonnentag, O.; Vargas, R.; Ma, S.; Baldocchi, D.D. Continuous observation of tree leaf area index at ecosystem scale using upward-pointing digital cameras. Remote Sens. Environ. 2012, 126, 116–125. [Google Scholar] [CrossRef]
- Qu, Y.; Han, W.; Fu, L.; Li, C.; Song, J.; Zhou, H.; Bo, Y.; Wang, J. Lainet—A wireless sensor network for coniferous forest leaf area index measurement: Design, algorithm and validation. Comput. Electron. Agric. 2014, 108, 200–208. [Google Scholar] [CrossRef]
- Qu, Y.; Zhu, Y.; Han, W.; Wang, J.; Ma, M. Crop leaf area index observations with a wireless sensor network and its potential for validating remote sensing products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 431–444. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, N.; Wang, M. Wireless sensors in agriculture and food industry—Recent development and future perspective. Comput. Electron. Agric. 2006, 50, 1–14. [Google Scholar] [CrossRef]
- Selavo, L.; Wood, A.; Cao, Q.; Sookoor, T.; Liu, H.; Srinivasan, A.; Wu, Y.; Kang, W.; Stankovic, J.; Young, D. Luster: Wireless sensor network for environmental research. In Proceedings of the 5th International Conference on Embedded Networked Sensor Systems, Sydney, Australia, 4–9 November 2007; pp. 103–116.
- Jin, R.; Li, X.; Yan, B.; Li, X.; Luo, W.; Ma, M.; Guo, J.; Kang, J.; Zhu, Z.; Zhao, S. A nested eco-hydrological wireless sensor network for capturing the surface heterogeneity in the midstream area of the Heihe River Basin, China. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2015–2019. [Google Scholar] [CrossRef]
- Hengl, T.; Rossiter, D.G.; Stein, A. Soil sampling strategies for spatial prediction by correlation with auxiliary maps. Soil Res. 2003, 41, 1403–1422. [Google Scholar] [CrossRef]
- Clark, P.J.; Evans, F.C. Distance to nearest neighbor as a measure of spatial relationships in populations. Ecology 1954, 35, 445–453. [Google Scholar] [CrossRef]
- Kim, J.; Guo, Q.; Baldocchi, D.; Leclerc, M.; Xu, L.; Schmid, H. Upscaling fluxes from tower to landscape: Overlaying flux footprints on high-resolution (Ikonos) images of vegetation cover. Agric. For. Meteorol. 2006, 136, 132–146. [Google Scholar] [CrossRef]
- Chen, B.; Coops, N.C.; Fu, D.; Margolis, H.A.; Amiro, B.D.; Black, T.A.; Arain, M.A.; Barr, A.G.; Bourque, C.P.A.; Flanagan, L.B. Characterizing spatial representativeness of flux tower eddy-covariance measurements across the Canadian carbon program network using remote sensing and footprint analysis. Remote Sens. Environ. 2012, 124, 742–755. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanré, D.; Deuze, J.L.; Herman, M.; Morcette, J.J. Second simulation of the satellite signal in the solar spectrum, 6s: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. Prospect + sail models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Vermote, E. Product Accuracy/Uncertainty: Mod09, Surface Reflectance; Atmospheric Correction Algorithm Product. In: MODIS Data Products Catalog (Eos Am Platform). Available online: http://modarch.gsfc.nasa.gov/MODIS/RESULTS/DATAPROD/ (accessed on 27 December 2000).
- Chen, J.M. Optically-based methods for measuring seasonal variation of leaf area index in boreal conifer stands. Agric. For. Meteorol. 1996, 80, 135–163. [Google Scholar] [CrossRef]
- Tan, B.; Woodcock, C.; Hu, J.; Zhang, P.; Ozdogan, M.; Huang, D.; Yang, W.; Knyazikhin, Y.; Myneni, R. The impact of gridding artifacts on the local spatial properties of MODIS data: Implications for validation, compositing, and band-to-band registration across resolutions. Remote Sens. Environ. 2006, 105, 98–114. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Garrigues, S.; Lacaze, R. LAI and FAPAR cyclopes global products derived from vegetation. Part 2: Validation and comparison with MODIS collection 4 products. Remote Sens. Environ. 2007, 110, 317–331. [Google Scholar]
- Yang, W.; Shabanov, N.; Huang, D.; Wang, W.; Dickinson, R.; Nemani, R.; Knyazikhin, Y.; Myneni, R. Analysis of leaf area index products from combination of MODIS terra and aqua data. Remote Sens. Environ. 2006, 104, 297–312. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Y.; Li, J.; Liu, Q.; Qu, Y.; Huete, A.R.; Xu, B.; Yin, G.; Zhao, J. An Optimal Sampling Design for Observing and Validating Long-Term Leaf Area Index with Temporal Variations in Spatial Heterogeneities. Remote Sens. 2015, 7, 1300-1319. https://doi.org/10.3390/rs70201300
Zeng Y, Li J, Liu Q, Qu Y, Huete AR, Xu B, Yin G, Zhao J. An Optimal Sampling Design for Observing and Validating Long-Term Leaf Area Index with Temporal Variations in Spatial Heterogeneities. Remote Sensing. 2015; 7(2):1300-1319. https://doi.org/10.3390/rs70201300
Chicago/Turabian StyleZeng, Yelu, Jing Li, Qinhuo Liu, Yonghua Qu, Alfredo R. Huete, Baodong Xu, Geofei Yin, and Jing Zhao. 2015. "An Optimal Sampling Design for Observing and Validating Long-Term Leaf Area Index with Temporal Variations in Spatial Heterogeneities" Remote Sensing 7, no. 2: 1300-1319. https://doi.org/10.3390/rs70201300
APA StyleZeng, Y., Li, J., Liu, Q., Qu, Y., Huete, A. R., Xu, B., Yin, G., & Zhao, J. (2015). An Optimal Sampling Design for Observing and Validating Long-Term Leaf Area Index with Temporal Variations in Spatial Heterogeneities. Remote Sensing, 7(2), 1300-1319. https://doi.org/10.3390/rs70201300