Detecting Clear-Cuts and Decreases in Forest Vitality Using MODIS NDVI Time Series
Abstract
:1. Introduction
2. Material
2.1. Study Area

2.2. MODIS Data
3. Methods
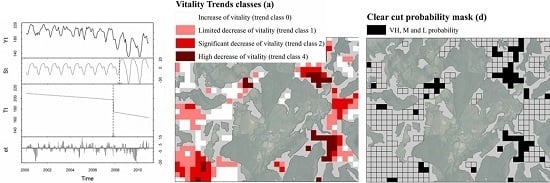
3.1. Map of Vitality Trends
- -
- Trend class 0: positive trends or trends not significantly different from the null slope, p-value > 0.05
- -
- Trend class 1: trends significantly negative, 0.05 > p-value > 0.01
- -
- Trend class 2: trends significantly negative, 0.01 > p-value > 0.001
- -
- Trend class 3: trends significantly negative, 0.001 > p-value
3.2. Breakpoint Detection
3.3. Clear-Cut Probability Model

3.3.1. Clear-Cut Reference Layer
3.3.2. Calibration of the Clear-Cut Probability Model
3.3.3. Assessment of the Accuracy of the Clear-Cut Detection Model
3.3.4. Effect of the Intra-Pixel Clear-Cut Proportion on the Accuracy of Clear-Cut Detection
4. Results
4.1. Dates and Magnitudes of Detected Breakpoints
- -
- The 2001–2002 period was characterized by a low negative breakpoint count, low magnitudes and limited standard deviations. No major climate anomalies or unscheduled clear-cutting activity was identified during this period.
- -
- The 2003–2004 period was characterized by a high negative breakpoint count with low magnitudes. This may be related to the direct impact of the 2003 summer drought and heat wave on the vitality of the forest stands [46]. After 2003, some stands were affected by pathogen attacks or by intense drying [47]. Furthermore, the low accumulation of reserves during the summer of 2003 led to a lack of activity during 2004 spring [48].
- -
- The 2005–2009 period was characterized by a medium negative breakpoint count with high magnitudes and standard deviations. Many clear-cuts were made further to the significant degradation of some stands after the 2003 summer drought. The summers of 2005 and 2006 were also characterized by a severe drought that may have impacted some forest stands. All the clear-cuts during this period can be associated with decaying stands presenting a high tree mortality rate.

| Period | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 1981–2010 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Annual | 1459 | 1153 | 1471 | 1240 | 1499 | 1048 | 1199 | 1298 | 1486 | 1277 | 1216 | 1409 |
| June, July, August | 580 | 459 | 614 | 199 | 539 | 283 | 338 | 491 | 481 | 450 | 362 | 461 |
4.2. Clear-Cut Probability Model
4.2.1. Clear-Cut Reference Layers

4.2.2. Relationship between Clear-Cut Probability and Breakpoint Magnitude
4.2.3. Definition of Clear-Cut Probability Classes


4.2.4. Accuracy of the Clear-Cut Detection Model

4.2.5. Impact of the Intra-Pixel Clear-Cut Proportion on the Accuracy of Clear-Cut Detection

4.3. Characterization of Clear-Cut Probability Classes
4.3.1. Spatial Distribution of Clear-Cut Probability Classes
| Clear-Cut Probability Classes | Breakpoint Magnitude Threshold | Clear-Cut Presence Probability | Proportion of Pixel in the Study Area (Total Area) | Intra-Pixel Clear-Cut Proportion in a MODIS Pixel |
|---|---|---|---|---|
| % | % (ha) | Mean and (standard deviation) % | ||
| VL – Very low probability of clear-cut | −10.5; +∞ | 3.8 | 80.1% (12 262 ha) | 3.8% (9.8) |
| L – Low probability of clear-cut | −17.9; −10.5 | 24.1 | 13.8% (2 120 ha) | 16.7% (20.1) |
| M – Medium probability of clear-cut | −26.4; −17.9 | 63.4 | 3.8% (585 ha) | 35.1% (24.8) |
| VH – Very high probability of clear-cut | − ∞; −26.4 | 94.4 | 2.7% (333 ha) | 69.2% (22.9) |
4.3.2. Annual Distribution of Clear-Cut Probability Classes

4.3.3. Relationship between Clear-Cut Probability Classes and Stand Vitality Trend Classes
- -
- Trend class 0: Increase or no significant decrease in vegetation activity, probably healthy stands;
- -
- Trend class 1: Limited decrease in vegetation activity, stand development uncertain;
- -
- Trend class 2: Significant decrease in vegetation activity, most forest stands are declining;
- -
- Trend class 3: Very high decrease in vegetation activity, declining stands, usually cut down.


5. Discussion
5.1. Regional Monitoring of Decrease in Forest Vitality
- (1)
- For the quantification of clear-cut areas, the medium and high clear-cut probability classes (class M and class VH) are of particular interest for users. By combining these two classes, the majority of large area clear-cuts are detected. However, the comparison with clear-cut reference data revealed an underestimation of approximately 16% of the total clear-cut area. The error of omission is mainly related to small clear-cut areas which do not generate a strong enough breakpoint to be included in class M and class VH. The majority of small clear-cut areas (less than 1 ha) are detected in class L, but this class also includes the signal for disturbances not related to clear-cuts. In this case, adding the results of this class to the clear-cut probability mask revealed a significant overestimation of about 176% of clear-cut area. For the quantification of clear-cut areas, it is preferable to limit the analysis to classes M and VH. Detecting small clear-cut areas using MODIS imagery remains out of reach [17]. We can assume that the model will be more efficient in other study areas where clear-cut areas are larger (e.g., Canada, Brazil). It may thus be necessary to assess the robustness of the method in areas with less fragmented stands and fewer stands impacted by clear-cuts.
- (2)
- For monitoring decreases in forest vitality, the interest of clear-cut probability classes lies in the possibility of establishing a mask that can be superimposed over a vitality trend map for the same period. By combining class L, class M and class VH to make the mask, we were able to identify, with a few errors, the location of areas impacted by clear-cuts. For the remaining pixels (class VL), the probability of the absence of clear-cuts was 96.2% (Figure 6).
5.2. Methodological Considerations
5.3. Future Works and Perspectives
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lindner, M.; Maroschek, M.; Netherer, S.; Kremer, A.; Barbati, A.; Garcia-Gonzalo, J.; Seidl, R.; Delzon, S.; Corona, P.; Kolström, M.; et al. Climate change impacts, adaptive capacity, and vulnerability of european forest ecosystems. For. Ecol. Manag. 2010, 259, 698–709. [Google Scholar] [CrossRef]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.H.; et al. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Van Mantgem, P.J.; Stephenson, N.L.; Byrne, J.C.; Daniels, L.D.; Franklin, J.F.; Fule, P.Z.; Harmon, M.E.; Larson, A.J.; Smith, J.M.; Taylor, A.H.; et al. Widespread increase of tree mortality rates in the western united states. Science 2009, 323, 521–524. [Google Scholar] [CrossRef]
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- White, M.A.; de Beurs, K.M.; Didan, K.; Inouye, D.W.; Richardson, A.D.; Jensen, O.P.; O’Keefe, J.; Zhang, G.; Nemani, R.R.; van Leeuwen, W.J.D.; et al. Intercomparison, interpretation, and assessment of spring phenology in north america estimated from remote sensing for 1982–2006. Glob. Chang. Biol. 2009, 15, 2335–2359. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Zeileis, A.; Culvenor, D. Phenological change detection while accounting for abrupt and gradual trends in satellite image time series. Remote Sens. Environ. 2010, 114, 2970–2980. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of maximum-value composite image from temporal AVHRR data. Int. J. Remote Sens. 1986, 1417–1434. [Google Scholar] [CrossRef]
- Glenn, E.; Huete, A.; Nagler, P.; Nelson, S. Relationship between remotely-sensed vegetation indices, canopy attributes and plant physiological processes: What vegetation indices can and cannot tell us about the landscape. Sensors 2008, 8, 2136–2160. [Google Scholar] [CrossRef]
- Teillet, P.M.; Staenz, K.; William, D.J. Effects of spectral, spatial, and radiometric characteristics on remote sensing vegetation indices of forested regions. Remote Sens. Environ. 1997, 61, 139–149. [Google Scholar] [CrossRef]
- Hlásny, T.; Barka, I.; Sitková, Z.; Bucha, T.; Konôpka, M.; Lukáč, M. Modis-based vegetation index has sufficient sensitivity to indicate stand-level intra-seasonal climatic stress in oak and beech forests. Ann. For. Sci. 2015, 72, 109–125. [Google Scholar] [CrossRef]
- Chéret, V.; Denux, J.P.; Ortisset, J.P.; Gacherieu, C. Utilisation de séries temporelles d’images satellitales pour cartographier le dépérissement des boisements résineux du sud massif central. Rendez-Vous Tech. 2011, 31, 55–62. [Google Scholar]
- Lambert, J.; Drénou, C.; Denux, J.P.; Balent, G.; Chéret, V. Monitoring forest decline through remote sensing time series analysis. GISci. Remote Sens. 2013, 50, 437–457. [Google Scholar]
- Lambert, J. Evaluation des Baisses de Vitalité des Peuplements Forestiers à Partir de Séries Temporelles D’images Satellitaires—Application aux Résineux du sud du Massif Central et à la Sapinière Pyrénéenne. Ph.D. Thesis, Institut National Polytechnique de Toulouse, Université Toulouse III, Toulouse, France, 2014. [Google Scholar]
- Zhan, X.; Sohlberg, R.A.; Townshend, J.R.G.; DiMiceli, C.; Carroll, M.L.; Eastman, J.C.; Hansen, M.C.; DeFries, R.S. Detection of land cover changes using MODIS 250 m data. Remote Sens. Environ. 2002, 83, 336–350. [Google Scholar] [CrossRef]
- Fraser, R.H.; Abuelgasim, A.; Latifovic, R. A method for detecting large-scale forest cover change using coarse spatial resolution imagery. Remote Sens. Environ. 2005, 95, 414–427. [Google Scholar] [CrossRef]
- Bucha, T.; Stibig, H.-J. Analysis of MODIS imagery for detection of clear cuts in the boreal forest in north-west russia. Remote Sens. Environ. 2008, 112, 2416–2429. [Google Scholar] [CrossRef]
- Jin, S.; Sader, S.A. modis time-series imagery for forest disturbance detection and quantification of patch size effects. Remote Sens. Environ. 2005, 99, 462–470. [Google Scholar] [CrossRef]
- Morton, D.C.; DeFries, R.S.; Shimabukuro, Y.E.; Anderson, L.O.; Espirito-Santo, F.D.B.; Hansen, M.; Carroll, M. Rapid assessment of annual deforestation in the brazilian amazon using MODIS data. Earth Interact. 2005, 9. [Google Scholar] [CrossRef]
- Bontemps, S.; Bogaert, P.; Titeux, N.; Defourny, P. An object-based change detection method accounting for temporal dependences in time series with medium to coarse spatial resolution. Remote Sens. Environ. 2008, 112, 3181–3191. [Google Scholar] [CrossRef]
- Hansen, M.C.; DeFries, R.S.; Townshend, J.R.G.; Sohlberg, R.; Dimiceli, C.; Carroll, M. Towards an operational MODIS continuous field of percent tree cover algorithm: Examples using AVHRR and MODIS data. Remote Sens. Environ. 2002, 83, 303–319. [Google Scholar] [CrossRef]
- Desclée, B.; Bogaert, P.; Defourny, P. Forest change detection by statistical object-based method. Remote Sens. Environ. 2006, 102, 1–11. [Google Scholar] [CrossRef]
- Hansen, M.C.; Roy, D.P.; Lindquist, E.; Adusei, B.; Justice, C.O.; Altstatt, A. A method for integrating MODIS and Landsat data for systematic monitoring of forest cover and change in the Congo basin. Remote Sens. Environ. 2008, 112, 2495–2513. [Google Scholar] [CrossRef]
- Potapov, P.; Hansen, M.C.; Stehman, S.V.; Loveland, T.R.; Pittman, K. Combining MODIS and Landsat imagery to estimate and map boreal forest cover loss. Remote Sens. Environ. 2008, 112, 3708–3719. [Google Scholar] [CrossRef]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Linke, J.; McDermid, G.; Masek, J.G.; Gao, F.; White, J.C. A new data fusion model for high spatial- and temporal-resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sens. Environ. 2009, 113, 1613–1627. [Google Scholar] [CrossRef]
- Lunetta, R.S.; Knight, J.F.; Ediriwickrema, J.; Lyon, J.G.; Worthy, L.D. Land-cover change detection using multi-temporal MODIS NDVI data. Remote Sens. Environ. 2006, 105, 142–154. [Google Scholar] [CrossRef]
- Vogelmann, J.E.; Xian, G.; Homer, C.; Tolk, B. Monitoring gradual ecosystem change using landsat time series analyses: Case studies in selected forest and rangeland ecosystems. Remote Sens. Environ. 2012, 122, 92–105. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- Alcaraz-Segura, D.; Liras, E.; Tabik, S.; Paruelo, J.; Cabello, J. Evaluating the consistency of the 1982–1999 NDVI trends in the Iberian Peninsula across four time-series derived from the AVHRR sensor: LTDR, GIMMS, FASIR, and PAL-II. Sensors 2010, 10, 1291–1314. [Google Scholar] [CrossRef] [PubMed]
- De Jong, R.; de Bruin, S.; de Wit, A.; Schaepman, M.E.; Dent, D.L. Analysis of monotonic greening and browning trends from global NDVI time-series. Remote Sens. Environ. 2011, 115, 692–702. [Google Scholar] [Green Version]
- Jacquin, A.; Sheeren, D.; Lacombe, J.-P. Vegetation cover degradation assessment in Madagascar savanna based on trend analysis of MODIS NDVI time series. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S3–S10. [Google Scholar] [CrossRef]
- Tüshaus, J.; Dubovyk, O.; Khamzina, A.; Menz, G. Comparison of medium spatial resolution ENVISAT-MERIS and TERRA-MODIS time series for vegetation decline analysis: A case study in central Asia. Remote Sens. 2014, 6, 5238–5256. [Google Scholar] [CrossRef]
- De Jong, R.; Verbesselt, J.; Schaepman, M.E.; de Bruin, S. Trend changes in global greening and browning: Contribution of short-term trends to longer-term change. Glob. Chang. Biol. 2012, 18, 642–655. [Google Scholar]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferriera, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation index. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. Timesat—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
- Roderick, M.; Smith, R.; Cridland, S. The precision of the NDVI derived from AVHRR observations. Remote Sens. Environ. 1996, 56, 57–65. [Google Scholar] [CrossRef]
- Reed, B.C. Trend analysis of time series phenology of north America derived from satellite data. GISci. Remote Sens. 2006, 43, 1–15. [Google Scholar] [CrossRef]
- Lambert, J.; Jacquin, A.; Denux, J.P.; Chéret, V. Comparison of two remote sensing time series analysis methods for monitoring forest decline. In Proceedings of the 6th International Workshop on the Analysis of Multi-Temporal Remote Sensing Images (Multi-Temp), Trento, Italy, 12–14 July 2011; pp. 93–96.
- Cleveland, R.; Cleveland, W.; McRae, J.; Terpenning, I. Stl: A seasonal-trend decomposition procedure based on Loess (with discussion). J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Makridakis, S.; Wheelwright, S.C.; Hyndman, R.J. Forecasting: Methods and Applications, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1998; p. 638. [Google Scholar]
- Fawcett, T. An introduction to roc analysis. Pattern Recog. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Alatorre, L.C.; Sanchez-Andres, R.; Cirujano, S.; Begueria, S.; Sanchez-Carrillo, S. Identification of mangrove areas by remote sensing: The roc curve technique applied to the northwestern Mexico coastal zone using landsat imagery. Remote Sens. 2011, 3, 1568–1583. [Google Scholar] [CrossRef] [Green Version]
- Sing, T.; Sander, O.; Beerenwinkel, N.; Lengauer, T. ROCR: Visualizing classifier performance in R. Bioinformatics 2005, 21, 3940–3941. [Google Scholar] [CrossRef]
- Hothorn, T.; Hornik, K.; Zeileis, A. Unbiased recursive partitioning: A conditional inference framework. J. Comput. Graph. Stat. 2006, 15, 651–674. [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Rebetez, M.; Mayer, H.; Dupont, O.; Schindler, D.; Gartner, K.; Kropp, J.P.; Menzel, A. Heat and drought 2003 in europe: A climate synthesis. Ann. For. Sci. 2006, 63, 569–577. [Google Scholar] [CrossRef]
- CRPF Midi-Pyrénées; ONF; EI-PURPAN. Dépérissement des Reboisements du sud Massif central—Etat des Lieux et Propositions D’analyse. Rapport d’étude. 2008, p. 43. Available online: www.crpf-midi-pyrenees.com/vousinformer/publication1-1_SANTE-DES-FORETS.htm (accessed on 10 March 2015).
- Bréda, N.; Huc, R.; Granier, A.; Dreyer, E. Temperate forest trees and stands under severe drought: A review of ecophysiological responses, adaptation processes and long-term consequences. Ann. For. Sci. 2006, 63, 625–644. [Google Scholar] [CrossRef]
- Hais, M.; Jonášová, M.; Langhammer, J.; Kučera, T. Comparison of two types of forest disturbance using multitemporal landsat TM/ETM+ imagery and field vegetation data. Remote Sens. Environ. 2009, 113, 835–845. [Google Scholar] [CrossRef]
- Jiménez-Valverde, A.; Lobo, J.M. Threshold criteria for conversion of probability of species presence to either–or presence–absence. Acta Oecol. 2007, 31, 361–369. [Google Scholar] [CrossRef]
- Liu, C.; Frazier, P.; Kumar, L. Comparative assessment of the measures of thematic classification accuracy. Remote Sens. Environ. 2007, 107, 606–616. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B. Detecting trends in forest disturbance and recovery using yearly landsat time series: 1. Landtrendr—Temporal segmentation algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Röder, A.; Hill, J.; Duguy, B.; Alloza, J.A.; Vallejo, R. Using long time series of landsat data to monitor fire events and post-fire dynamics and identify driving factors. A case study in the Ayora region (eastern Spain). Remote Sens. Environ. 2008, 112, 259–273. [Google Scholar] [CrossRef]
- Drusch, M.; del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’S optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Justice, C.O.; Vermote, E.; Townshend, J.R.G.; Defries, R.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.H.; et al. The moderate resolution imaging spectroradiometer (MODIS): Land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lambert, J.; Denux, J.-P.; Verbesselt, J.; Balent, G.; Cheret, V. Detecting Clear-Cuts and Decreases in Forest Vitality Using MODIS NDVI Time Series. Remote Sens. 2015, 7, 3588-3612. https://doi.org/10.3390/rs70403588
Lambert J, Denux J-P, Verbesselt J, Balent G, Cheret V. Detecting Clear-Cuts and Decreases in Forest Vitality Using MODIS NDVI Time Series. Remote Sensing. 2015; 7(4):3588-3612. https://doi.org/10.3390/rs70403588
Chicago/Turabian StyleLambert, Jonas, Jean-Philippe Denux, Jan Verbesselt, Gérard Balent, and Véronique Cheret. 2015. "Detecting Clear-Cuts and Decreases in Forest Vitality Using MODIS NDVI Time Series" Remote Sensing 7, no. 4: 3588-3612. https://doi.org/10.3390/rs70403588
APA StyleLambert, J., Denux, J. -P., Verbesselt, J., Balent, G., & Cheret, V. (2015). Detecting Clear-Cuts and Decreases in Forest Vitality Using MODIS NDVI Time Series. Remote Sensing, 7(4), 3588-3612. https://doi.org/10.3390/rs70403588