Next Article in Journal
A Hidden Markov Models Approach for Crop Classification: Linking Crop Phenology to Time Series of Multi-Sensor Remote Sensing Data
Next Article in Special Issue
The Effects of Point or Polygon Based Training Data on RandomForest Classification Accuracy of Wetlands
Previous Article in Journal
Detecting Clear-Cuts and Decreases in Forest Vitality Using MODIS NDVI Time Series
Previous Article in Special Issue
Adjusting Lidar-Derived Digital Terrain Models in Coastal Marshes Based on Estimated Aboveground Biomass Density
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 7
Issue 4
10.3390/rs70403613
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Operational Actual Wetland Evapotranspiration Estimation for South Florida Using MODIS Imagery

by
Cristobal N. Ceron
1,
Assefa M. Melesse
1,*,
René Price
1,2,
Shimelis B. Dessu
1 and
Hari P. Kandel
1
1
Department of Earth and Environment, Florida International University, Miami, FL 33199, USA
2
Southeast Environmental Research Center, Florida International University, Miami, FL 33199, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2015, 7(4), 3613-3632; https://doi.org/10.3390/rs70403613
Submission received: 13 October 2014 / Revised: 13 March 2015 / Accepted: 18 March 2015 / Published: 26 March 2015
(This article belongs to the Special Issue Towards Remote Long-Term Monitoring of Wetland Landscapes)
Browse Figures
Versions Notes

Abstract

:
Evapotranspiration is a reliable indicator of wetland health. Wetlands are an important and valuable ecosystem on the South Florida landscape. Accurate wetland Actual Evapotranspiration (AET) data can be used to evaluate the performance of South Florida’s Everglades restoration programs. However, reliable AET measurements rely on scattered point measurements restricting applications over a larger area. The objective of this study was to validate the ability of the Simplified Surface Energy Balance (SSEB) approach and the Simple Method (also called the Abtew Method) to provide large area AET estimates for wetland recovery efforts. The study used Moderate Resolution Imaging Spectroradiometer (MODIS) sensor spectral data and South Florida Water Management District (SFWMD) solar radiation data to derive weekly AET values for South Florida. The SSEB-Simple Method approach provided acceptable results with good agreement with observed values during the critical dry season period, when cloud cover was low (rave (n = 59) = 0.700, pave < 0.0005), but requires further refinement to be viable for yearly estimates because of poor performance during wet season months, mainly because of cloud contamination. The approach can be useful for short-term wetland recovery assessment projects that occur during the dry season and/or long term projects that compare site AET rates from dry season to dry season.

Graphical Abstract

1. Introduction

Wetlands provide a wide range of services and benefits to a region. They provide erosion protection to coastlines and sediment control for large areas [1]. Wetlands provide extensive habitats for a wide range of wildlife, including nursery habitats for numerous fish and shellfish species and breeding, nursing, and migratory habitat for large numbers of water birds [2]. Wetlands are habitats for many species of reptiles, amphibians, some mammals, and a myriad of insect and plant species [1,2,3]. Wetlands act as a giant filter cleaning both natural and man-made waste, help recharge aquifers, and provide drinking water for communities [2,3]. In addition, wetlands can be ideal sites for recreational activities such as camping, fishing, and hunting and for educational and scientific study [4].
Loss of wetlands is a worldwide problem, and the United States has experienced major losses in recent history. It is estimated that during the late part of the 20th century, the United States was losing wetlands at the rate of 60,000 acres per year [5]. Fortunately, concerted conservation and remediation efforts have helped slow the loss of wetland environments. South Florida is dominated by three major ecosystems: natural, agricultural, and urban. The eastern edge of South Florida is covered mostly by urban sprawl in close proximity to extensive natural areas to the west and south. These natural areas include Everglades National Park, Big Cypress National Preserve, Biscayne National Park, and many smaller wild wetland areas. Agricultural lands are scattered across the South Florida landscape, particularly in the Everglades Agricultural Area near and around the southern edge of Lake Okeechobee. Understanding the interactions between the three closely linked ecological systems can help improve existing design approaches of wetland restoration and conservation plans that balance the needs of people with environmental sustainability.
The unique and diverse characteristics of wetlands have indirectly contributed to their destruction in many areas. Over the years, wetlands have been drained or had their water sources diverted to control flooding in developed (or soon to be developed) areas [1,4]. Wetlands also have been drained to take advantage of their nutrient-rich soils for agricultural production or grazing of livestock [4,6]. Wetlands that are not directly developed continue to suffer from the effects of urban and agricultural development. Runoff from agricultural and urban areas can pollute wetlands, affecting the natural chemistry of these areas [1]. Many of these problems currently affect one of the largest wetland environments in the world: South Florida’s Everglades National Park.

Evapotranspiration as an Indicator of Wetland Recovery

With many restoration efforts now underway, evaluations are necessary to assess the success of the restoration methods being used. Water has a direct impact on the ecosystem dynamics of wetlands, and hydrologic variables such as evapotranspiration, flood duration, flow velocity, and flow variability can be used to gauge wetland health [7,8,9]. Of these hydrological variables, evapotranspiration (ET) proves a reliable indicator of hydrological recovery [10]. ET is the combined measurement of water being lost to the atmosphere as a result of evaporation from open water sources and transpiration from plants. In general, ET is the principal method of water loss in South Florida wetlands. For example, the Everglade receives a yearly average rainfall of around 1270 mm and loses an estimated 1020 mm annually to ET [11]. The difference between rainfall and ET can be used to measure the workings of healthy wetland ecosystems.
Various methods exist for estimating ET. Traditional means, such as the pan, Bowen ratio, eddy correlation, and aerodynamic techniques, estimate ET at point locations. These methods are costly, time consuming, and require elaborate and sensitive measurement equipment [12]. A root-zone soil water balance approach based on a water budget is also a technique used to estimate ET as a residual variable. Quantifying each component of the soil water balance is less appealing in terms of time, labor, and money requirements. Relatively simpler point methods use lysimeter instrumentation [13]. Although the traditional methods estimate ET on a point basis, recent methods have found success using remotely sensed imagery for estimates at various spatial scales [14,15]. In contrast to point measurements, remote sensing has the capacity to acquire spectral signatures instantaneously for large areas of the watershed across multiple electromagnetic (EM) wavebands and spatial scales. Data in multiple EM wavebands allow for the extraction of land cover, vegetation cover, emissivity, albedo, surface temperature, energy flux information, and data at regional scales allow for greater spatial coverage than possible with in-situ methods.
Various researchers have used remote sensing tools to estimate wetland evapotranspiration and energy fluxes in various regions of the world [16,17,18,19,20,21,22,23,24,25]. A healthy wetland area will be fully or partially inundated for most of the year. The water will provide the necessary conditions for wetland flora and fauna to grow and thrive. The combination of surface water and healthy plant populations will cause high rates of both evaporation and transpiration (high ET). Conversely, an unhealthy and dry wetland area lacks the necessary flooding to maintain the growth of native flora. The lack of above-surface water and healthy plant population result in low evaporation and transpiration rates (low ET). Hence, measuring the ET rates of a restored wetland and comparing them with the ET rates of healthy wetlands can provide a measure of how well the treated wetland is recovering. Furthermore, studying ET rates over prolonged periods of time can provide information on the speed and efficiency of the restoration techniques applied at a given site. Although ET is recognized as an important measure of wetland health, identifying the best-suited technique for measurement of ET in the South Florida region is a credible research question. We tested one such approach.
Rainfall measurements are made at numerous locations across South Florida, but ET stations are rare. Satellite measurements allow for wide spatial coverage between land-based stations, and provide visible access to relatively inaccessible areas such as the Everglades. The objective of this study was to assess and validate a model that will provide weekly Actual Evapotranspiration (AET) estimates for the South Florida region using the “Simple Method” technique in combination with the Simplified Surface Energy Balance Method (SSEB), which we describe in the methods section. The study produced AET estimates and maps for the South Florida region, with a focus on wetland areas in and around Everglades National Park and Big Cypress National Preserve. These products can be used operationally to assess the progress of wetland restoration. Hence, results of this research will facilitate future restoration assessment studies by providing a simple and accessible method of calculating ET values.

2. Study Area, Data Set and Methods

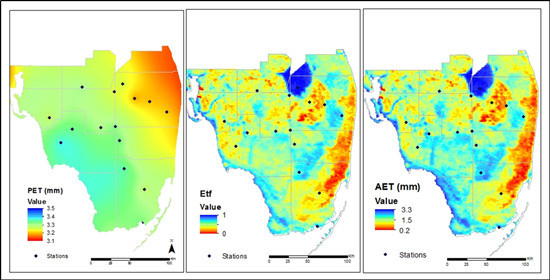
2.1. Description of the Study Area

South Florida (Figure 1a) offers a perfect microcosm of the threats faced by the world’s wetlands and the efforts being made to protect these unique ecosystems from disappearing. The extent of our study covered the South Florida region, including the Kissimmee River basin, water conservation areas, Everglades National Park, Big Cypress National Preserve, and other areas under the South Florida Water Management District. The study area is a mosaic of land use, where wetland, agricultural, and urban ecosystems exist side by side.
Remotesensing 07 03613 g001 1024
Figure 1. (a) South Florida study area; (b) Control evapotranspiration (ET) eddy covariance tower locations.
Figure 1. (a) South Florida study area; (b) Control evapotranspiration (ET) eddy covariance tower locations.
Remotesensing 07 03613 g001

2.2. Data Set

Data sources for the study included solar radiation, evapotranspiration from eddy covariance experimental sites, and MODIS-based surface temperature. Solar radiation data were downloaded from the South Florida Water Management District’s DBHYDRO online database [26]. We chose 15 stations for this study (Table 1 and Figure 1a). Daily mean solar radiation data were downloaded for these stations for the 1 January 2008 to 31 December 2010 period. The stations were chosen to cover the study area and we selected years for which control data were available. Solar radiation data for these stations are available as instant (30 min interval) values or as a daily mean solar radiation value (KW/m2). For the current study, mean values were used.
Table
Table 1. List and location of solar radiation stations.
Table 1. List and location of solar radiation stations.
StationBasinLatitudeLongitudeCountyDescription
3AS3WXConservation area 3A25°51′6.2″80°45′58.5″Miami-DadeWater Conservation Area 3 (WCA3) weather station, tree islands.
Ave MariaFaka Union26°18′6.09″81°25′52.9″CollierTown of Ave Maria weather station
BELLE GLS-2_6_726°39′24.6″80°37′48.1″Palm BeachBelle Glade weather station
BIG CY SIRFeeder Canal26°19′17.3″81°4′4.24″HendryBig Cypress at Seminole Indian Reservation
CFSWS-426º44′6.23″80°53′43.2″HendryClewinston field station weather station
ENR308STA-1W26°37′21.2″80°26′20.2″Palm BeachWeather station near interior levee in cell 3
FPWXEstero Bay26°25′57.3″81°43′24.3″LeeFlint Pen Strand weather station
JBTSC-111 Coastal25°13′28.4″80°32′24.2″Miami-DadeJoe Bay, approx. 9.5 km from Gilbert’s Res. Overseas Hwy boat ramp, key Largo
L006Lake Okeechobee26°49′21.2″80°46′58.2″Palm BeachLake Okeechobee tower South (#6)
LOXWSConservation area 126°29′56.3″80°13′20.2″Palm BeachLoxahatchee weather station at CA1-8C and L-40
ROTNWXSTA-5/626°19′56.8″80°52′53.1″BrowardRotenberger tract weather station
S140WConservation Area 3A26°10′16.7″80°49′33.6″BrowardS140 weather station on levee L28 near Alligator Alley
S331WL-31NS25°36′37.5″80°30′34.6″Miami-DadeS-331 weather station on L-31N
S78WEast Caloosahatchee26°47′23.2″81°18′10.3″GladesS-78 weather station on Caloosahatchee River at Ortona
SGGEWXFaka Union26°8′43.3″81°34′32.3″CollierSouthern Golden Gate Estates weather station
Surface temperature data from the Moderate Resolution Imaging Spectroradiometer (MODIS) onboard NASA’s Terra satellite were used in this study. The MODIS instrument has 36 spectral bands to take images of the Earth at resolutions of 250, 500, and 1000 meters, providing information on cloud/aerosol properties, ocean phytoplankton densities, and surface and cloud temperature, among other atmospheric, land, and ocean surface phenomena. MODIS provided the necessary temporal (weekly) dimensions needed to estimate weekly evapotranspiration rates across the expansive South Florida Region. The 1000 m spatial resolution of the thermal band of MODIS is also sufficient to capture the spatial variability of evapotranspiration.
We downloaded the MOD11A2 MODIS Land Surface Temperature (LST) and Emissivity eight-day product from the Land Processes Distribution Active Archive Center [27]. The MODIS sensor collects raw digital signals to calculate reflectance and Earth-exiting radiance [28]. The MOD11A2 product consists of 12 layers, including clear day/night average LSTs and emissivity values as well as several quality assurance layers. LST is calculated using MODIS radiance data (MOD021KM) in combination with MODIS geolocation data (MOD03), atmospheric temperature and water profile data (MOD07_L2), cloud mask data (MOD35_L2), and land-cover (MOD12Q1) and snow cover data (MOD10_L2) [29]. The MOD11A2 product is composited from eight days of daily 1-km LST products (MOD11A1) to create average (across the eight days) clear-sky LSTs. To be classified as “clear sky” an image or pixel must pass the “clear sky” validation process detailed by Ackerman [30]. MODIS products are projected onto a sinusoidal grid of “tiles” composed of 36 columns and 18 rows. The study area is located in tile (10, 6), where the first number corresponds to the column and the second to the row of the grid. Images from 1 January 2008 to 31 December 2010, were downloaded from the U.S. Geological Survey’s (USGS) EarthExplorer ordering interface [31]. There are 46 eight-day intervals per year, resulting in a total of 138 time intervals across the three years we studied.
USGS eddy covariance AET data were used to test the validity of the modeled AET data. The USGS data were part of an earlier study [32] that collected data from five sites located inside Big Cypress National Preserve (Figure 1b). Each site is distinguished by the type of land cover the ET measuring equipment was installed upon (see descriptions in Table 2).
Table
Table 2. Control/observed site detailed descriptions.
Table 2. Control/observed site detailed descriptions.
Site NameLatitudeLongitudeHeight of EC Tower (m)Land Cover Description
Dwarf Cypress25°45′45″80°54′27″16.5Dwarf cypress and sawgrass (herbaceous vegetation)
Cypress Swamp25°45′10″81°06′01″38Tall cypress strand
Pine Upland25°59′59″80°55′29″38Pine upland and cypress domes
Wet Prairie25°44′41″80°56′24″3.6Wet prairie with short (<1 m) sawgrass (herbaceous vegetation)
Marsh26°11′57″81°15′58″3.6Deep-water marsh with tall (1–2 m) sawgrass (herbaceous vegetation).

2.3. Methods

2.3.1. The Simple Method and the Simplified Surface Energy Balance Equation

This study calculated weekly AET values using a combination of methodologies. AET is given by the following equation (Equation (1)):
A E T = ( E T f ) ( P E T )
where PET refers to potential evapotranspiration and ETf is the evapotranspiration fraction. Potential evapotranspiration is an estimate of the maximum possible amount of water that can evapotranspire from an area. The evapotranspiration fraction (ETf) is a coefficient to estimate what portion of the total available water will actually evapotranspire. ETf can be calculated in several ways and can include factors such as surface temperature, atmospheric pressure, wind speed, and humidity as inputs.
In this study, two methods—one for calculating PET and one for calculating ETf—were used together to provide AET estimates for the South Florida region. PET was calculated using the Simple Model [33], also called the “Simple Method”. The Simple Model was developed using lysimeter measurements of open water evaporation and of wetland evapotranspiration in the South Florida region [33]. Through this study, it was found that in South Florida, evaporation from shallow lakes, evapotranspiration from wetlands, and potential evaporation occur at very similar rates [33]. With this in mind, the Simple Method [15] proposed a simple equation (Equation (2)) relating the PET to solar radiation.
P E T = K 1 R s λ
where Rs is solar radiation in MJ/m2-day, λ is the latent heat of vaporization of water at 20 °C (2.45 MJ/kg), and K1 is a calibration coefficient equal to 0.53 for the South Florida region [33].
The value of ETf was calculated using the SSEB equation [34]. The SSEB is derived from a more complex model Surface Energy Balance Algorithm (SEBAL) [35,36,37]. SEBAL uses an energy conservation equation to estimate evapotranspiration rates. The SSEB model utilizes surface temperature measurements to calculate the ET fraction. SSEB assumes areas with high surface temperature will have low ET rates (low ET fraction value) and areas with low surface temperature will have high ET rates (high ET fraction values). When incoming solar radiation is intercepted by a dry, poorly vegetated area, most of that energy is used, heating up the ground and atmospheric layer right above the ground (the H and G terms in the energy conservation equation). The energy then raises the overall temperature of area. When incoming solar radiation is intercepted by a wet, vegetated area, a large portion of the energy goes into latent heat that is powering the phase change from water to water vapor (the λE term in the energy conservation equation). As phase changes occur without an increase in temperature, these wet areas remain relatively cool. The SSEB [38] uses remotely sensed surface temperature to calculate the ET fraction (Equation (3)):
E T f = ( T h − T x ) ( T h − T c )
where Th and Tc are the average hottest and average coldest temperatures, respectively, of a land surface temperature (LST) image provided by a satellite-mounted spectroradiometer. The value of Tx is the LST value for an area of interest within the satellite image (“scene”). The SSEB model equation for ETf relied on satellite LST data from MODIS.2.3.2 Evapotranspiration Fraction (ETf) Calculation.
The eight-day daytime 1km LST layer (layer 1) was extracted from the MOD11A2 product. High temperature (Th) and low temperature (Tc) benchmarks specific to the scene area through the study years were required for the calculation. To minimize the effect of local extreme temperature values (outliers) on the ETf estimation, each pixel temperature value was adjusted by a moving-average window of the surrounding eight pixels (a 3 × 3 pixel area). Corresponding Th and Tc values were extracted from the resulting image layer. The ETf equation was then applied to the original (un-averaged) LST image pixel by pixel using Equation (3). The resulting temperature layer had values greater than one and less than zero, which correspond to temperature values higher than the average high temperature and lower than the average low temperature. These values corresponded to outlier pixels and were adjusted by converting negative values to ETf = 0 (no evapotranspiration from that pixel) and converting values greater than one to ETf = 1 (pixels evapotranspire at PET rates). The final layer contained ETf values between 0 and 1.

2.3.2. Potential Evapotranspiration (PET) Calculation

Daily mean solar radiation values provided an estimate of average solar radiation received by a 1 m × 1 m square of land in one second on a particular day. The total solar radiation received by that square in one day can be determined by Equation (4):
R s = ( 24 × 3600 × R i ) 1000
where Rs is the mean daily solar radiation in MJ/m2/day and Ri is the mean solar radiation in KW/m2. The factor of 1000 is used to convert KW to MW and the (24 × 3600) term corresponds with the number of seconds in one day. The converted values were then used to calculate PET (mm/day) for each day using the Simple Method in Equation (2).
Daily PET values were averaged into eight-day periods to match the MODIS satellite data. Each year (2008–2010) was averaged separately; that is, the first period for 2008 was from 1 January to 8 January and the last period was from 26 December to 31 December (the last period contains less than 8 days). This pattern began again for 2009 and 2010.
Point PET data were uploaded to a GIS point layer for each monitoring station. The point layer was used to create interpolated PET surfaces using a Bayesian-Kriging methodology for each eight-day period with the corresponding 15 data points for each period. Bayesian-Kriging provided the most consistent results of any of the available interpolation methods and was recommended because of the small number of data values available for the interpolation [39]. Once the interpolated PET layer was created, it was expanded to cover the whole South Florida region and saved as a new raster layer to match the format of the ETf layer. This process was conducted for all eight-day periods from 1 January 2008 to 31 December 2010.

2.3.3. Actual Evapotranspiration (AET) Calculation

Equation (1) was used to create the final AET layer. The calculation was carried out pixel by pixel and the output of the multiplication process was the modeled AET map of the study area. The final output was total mm AET per eight-day interval at a spatial resolution of 0.96 km by 0.96 km.

2.3.4. Model Evaluation

Correlation between the control (eddy covariance data) and experimental or modeled AET and PET data sets were checked for normality using both histogram analysis and the Shapiro-Wilk normality test. The test was done for all five control sites separately. The correlation was tested using the Pearson’s correlation coefficient and the Spearman’s correlation coefficient (Figure 2).
The full data set was separated into dry and wet season subsets. The dry set included values from November to April of each year and the wet set included values from May to October of each year. Both the dry season and wet season datasets were tested for normality and correlation. ETf, PET, and AET maps were created for 1 January 2008 to 31 December 2010. Each map contained average data of eight-day observation periods and was labeled using the Julian date of the first day of observation within the corresponding eight-day period (Figure 3). ETf, PET, and AET data can be extracted for any pixel within a corresponding map, but for analysis and validation of the model, only the values of the five control sites (pixels) were extracted from the maps.
Remotesensing 07 03613 g002 1024
Figure 2. Correlation test results between control site ET and modeled ET. Error bars represent confidence level (p-value).
Figure 2. Correlation test results between control site ET and modeled ET. Error bars represent confidence level (p-value).
Remotesensing 07 03613 g002
Remotesensing 07 03613 g003 1024
Figure 3. Potential evapotranspiration (PET), the evapotranspiration fraction (ETf), and actual evapotranspiration (AET) maps for observation period 2008025. This period includes data from 25 January to 1 February of 2008.
Figure 3. Potential evapotranspiration (PET), the evapotranspiration fraction (ETf), and actual evapotranspiration (AET) maps for observation period 2008025. This period includes data from 25 January to 1 February of 2008.
Remotesensing 07 03613 g003

3. Results and Discussion

3.1. Correlation between Modeled and Observed AET

The modeled AET was in close agreement with observed eddy covariance data, with a correlation coefficient of rave (n = 59) = 0.700 and pave < 0.0005 for the dry season, when wetland management is critical because of high temperatures and the absence of rainfall (Figure 2). For the wet season, the MODIS images were covered with clouds and the LST data were not accurate enough to give results as good as that of the dry season.

3.2. Modeled AET Temporal Variation

The model showed varying degrees of success depending on the time of year. There was a clear distinction between certain parts of each year. MODIS temperature data for hotter, wetter months (August and September) had a higher incidence of missing data (due to cloud cover) and pixels of lower temperature values than images acquired during cooler, dryer months (December, January). Hence, the data were stratified by a “Dry” period and a “Wet” period to see how each distinct season affected the overall trends observed in the complete dataset.
Dry months experienced closer agreement between model and control data (Figure 4 and Figure 5), with an average RMSE and bias across the five sites of 0.602 mm and −0.213 mm, respectively (Table 3). Furthermore, control and modeled AET values showed significant correlation at all five sites, with the lowest correlation occurring at the Marsh site (r(n = 59) = 0.568) and the highest occurring at the Dwarf Cypress Swamp (r(n = 59) = 0.791) (Figure 3). Control and modeled AET values showed little agreement during wet season months (Figure 6 and Figure 7). The average RMSE and bias for the five control sites were 1.725 and −1.281, respectively (Table 4). Wet season control values did show a stronger correlation with PET values, demonstrating that, as expected, AET tends to be high and close to the PET values during the wet season (Figure 5).
Table
Table 3. Statistical comparison between control (“c”) and modeled (“m”) AET for dry season data.
Table 3. Statistical comparison between control (“c”) and modeled (“m”) AET for dry season data.
SiteMeanC (mm)STDC (mm)CVC (%)Meanm (mm)STDm (mm)CVm (%)Bias (mm)RMSE (mm)Bias/Meanc (%)RMSE/Meanc (%)
Cypress Swamp2.3020.94340.81.9440.76139−0.3570.697−15.530.3
Pine Upland1.8160.51328.21.7740.67437.8−0.0420.463−2.325.5
Dwarf Cypress2.2090.63128.42.0030.71835.7−0.2060.494−9.322.3
Marsh2.0130.61730.61.9680.75338.1−0.0450.655−2.232.6
Wet Prairie2.360.54923.21.9460.77539.7−0.4140.701−17.529.7
Average2.140.65130.21.9270.73638.1−0.2130.602−9.428.1
The validation sites were all located in wetland environments and the k-coefficient (k = 0.53) used in the Simple Equation corresponds to a wetland environment. A new k value may be needed to improve the PET values for urban and agricultural settings. A larger number of validation sites, covering both agricultural and urban areas, are needed to assess the accuracy of the current model when predicting both PET and AET rates across urban and agricultural areas.
Remotesensing 07 03613 g004 1024
Figure 4. Dry season control AET, modeled AET, and PET values at control sites.
Figure 4. Dry season control AET, modeled AET, and PET values at control sites.
Remotesensing 07 03613 g004
Remotesensing 07 03613 g005 1024
Figure 5. Dry season comparisons between control and modeled AET data.
Figure 5. Dry season comparisons between control and modeled AET data.
Remotesensing 07 03613 g005
Remotesensing 07 03613 g006 1024
Figure 6. Wet season control AET, modeled AET, and PET values at control sites.
Figure 6. Wet season control AET, modeled AET, and PET values at control sites.
Remotesensing 07 03613 g006
Remotesensing 07 03613 g007 1024
Figure 7. Mean control and modeled AET values for wet, dry, and full seasonal data.
Figure 7. Mean control and modeled AET values for wet, dry, and full seasonal data.
Remotesensing 07 03613 g007
Table
Table 4. Statistical comparison between control (“c”) and modeled (“m”) actual evapotranspiration (AET) for wet season data.
Table 4. Statistical comparison between control (“c”) and modeled (“m”) actual evapotranspiration (AET) for wet season data.
SiteMeanC (mm)STDC (mm)CVC (%)Meanm (mm)STDm (mm)CVm (%)Bias (mm)RMSE (mm)Bias/Meanc (%)RMSE/Meanc (%)
Cypress Swamp3.5430.80822.71.8890.91848.4−1.9542.013−46.756.8
Pine Upland2.7840.47116.81.8240.83445.5−0.961.448−34.552.0
Dwarf Cypress3.3810.55616.41.9730.95748.3−1.4091.954−41.757.8
Marsh2.7950.45316.11.9240.92547.9−0.8711.409−31.250.4
Wet Prairie3.4430.53315.41.9340.94848.8−1.5091.8−43.852.3
Average3.1890.56417.51.9090.91647.8−1.2811.725−39.653.9

3.3. Comparisons with Other Studies

Several previous studies have provided ET estimates for the South Florida region [11,40,41,42,43]. All showed strong seasonal patterns, as seen in this study [11,41,42,43], where the highest ET rates occurred during wet season months and lower ET rates occurred during dry season months. Results have shown poor performance for wet-season and satisfactory performance for dry-season ET estimation. Evapotranspiration of wetlands is higher during the dry seasons, when solar radiation is higher and wetland management is critical. Due to the seasonal variation in model prediction, direct comparisons between seasonal ET rates from this model and others were made. Abtew [33] used lysimeters to calculate ET of a marsh site from 1993 to 1994. Average ET of dry season months (November to April) was 3.16 mm/day in 1993 (January estimate not included) and 2.74 mm/day in 1994. The lowest dry season ET of the study period corresponded to January of 1994 (1.9 mm/day) and the highest ET corresponded to April of 1993 (4.8 mm/day). Douglas [41] conducted a broader study using the Priestly-Taylor and Penman-Monteith methods to calculate ET for a wide range of sites across Florida including marsh sites inside Everglades National Park and a few pine forest sites in Northern Florida. The marsh sites showed an average ET of 3.0 mm/day and the pine forest sites had an average ET of 2.05 mm/day [38]. Estimates from lysimeter sites (sawgrass and cattail) carried out from 1996 to 1999 gave dry season ET average estimates ranging from 1.42 mm/day (January cattail) to 4.9 mm/day (April sawgrass) [44]. Dry season ET estimates ranging from about 1.5 mm/day to about 4.5 mm/day are seen in the majority of ET studies of wetland regions across Florida [11,41,42,43].
The ET estimates calculated in this study fell within the range discussed in the aforementioned studies (Table 5). For example, the marsh site had a dry season average of 1.97 mm/day over the observation period, which was lower than the average seen at similar sites in the Abtew [33] and Douglas [41] studies. Similarly, the Pine Upland site had an average dry season of 1.77 mm/day, which again was lower than the ET estimates of previous studies. The control values provided by Shoemaker [32], 2.01 mm/day for the Marsh site and 1.82 mm/day for the Pine Upland site, showed that the low dry season ET estimates were not necessarily due to poor model performance, but that the dry season ET rates estimated during the study period were lower than those of previous study periods. The average experimental dry season ET across all five control sites was 1.92 mm/day, which fell within the range of ET values observed in previous studies [11,33,41]. The average control dry season AET across all five sites was 2.14 mm/day. These averages show that the model did tend to underestimate the AET values for all five sites.
Table
Table 5. Comparison of evapotranspiration (ET) values from different studies.
Table 5. Comparison of evapotranspiration (ET) values from different studies.
SourceDry SeasonWet SeasonSite
SSEB−Simple Method1.92 mm/day1.91 mm/dayAverage of 5 sites
Mao et al. [44]1.42 mm/dayto 4.9 mm/dayLysimeter (sawgrass & cattail)
German [11], Douglas et al. [41], Abtew [42], Bidlake et al. [43]1.5 mm/day4.5 mm/dayWetland regions
Abtew [33]3.16 mm/day in 1993 2.74 mm/day in 1994 Lysimeter marsh site from 1993 to 1994
Allen [45] has stated that AET estimates through remote sensing methods can expect errors (defined as one standard deviation away from the true mean) between 10% and 30%. The metric in this study that provided the most similar definition of error as defined by Allen was RMSE/Meanc (mean of the control values), which also gave an estimate of how far away the experimental values fell from the true values (in this case taken to be the control values). The average RMSE/Meanc of the five control sites was 28.1%, meaning that, on average, the experimental values were about 30% away from the control values. In a similar study, Jiang [46] used daily LST data to provide daily AET estimates in the South Florida region. His results showed a range for RMSE/Meanc from 23.1% to 45% across 11 sites, with an average of 30.8%, which again is similar to the RMSE/Meanc observed across the five sites used in this study for dry season months. In general, the Simple/SSEB method provided AET estimates in line with previous studies using relatively simple techniques that did not require the technical expertise, large equipment and maintenance costs, or time needed by other methods [41,42,47,48].

3.4. Limitations and Suggested Improvements

The calculation of AET estimates carried out in this study faced common challenges identified in similar wetland AET estimation studies. First and foremost, prolonged periods of cloud cover during wet season months had a deleterious effect on the LST data provided by the MODIS sensor. This led to the underestimation of ETf and, consequently, AET estimates. Jiang [46] also faced the problem of cloudy images and applied a model where missing pixels were approximated by using neighboring pixels and pixels from previous observations. This can work, but not when a large portion of the observation area is cloud covered for the better part of eight days (from this study). The ability to acquire useful LST data under cloudy conditions would definitely have improved the AET estimates provided by this study and remains a major challenge for any methodology that relies on remotely sensed data to provide useful AET estimates for South Florida or other cloud-prone regions.
Missing and underestimated LST data from MODIS was the main source of error for the final AET values for the wet season. The eight-day composite temperature images were created by averaging the “clear sky” pixels from eight single-day temperature images. Defining a “clear sky” pixel is a rather complex endeavor, as detailed in Ackerman [30], but a clear sky pixel is free from most, if not all, cloud contamination. To have a missing pixel in the eight-day composite image, the majority (or all) of the single-day images must have that pixel missing, as well (i.e., cloud covered). But, there is a chance that a clear sky pixel exists within one of the eight single-day images. The single-day LST data can overcome poor eight-day LST images where temperature values can be used to calculate the ETf for the pixel of interest. For now, the more appropriate solution for this problem is the acquisition of better temperature data, which may be available from other satellite based sensors with thermal bands, such as ASTER and Landsat [49].
Improvements to the ETf estimation procedure can also help improve the accuracy of final AET estimates. This is currently being done in other studies that incorporate more complex techniques of calculating Th and Tc [38,50]. The approaches being tested may increase the accuracy of the final AET estimates, but they do so at the expense of simplicity. The use of other remote sensing platforms that can provide higher resolution data and/or complement the data provided by MODIS would also improve the accuracy of AET estimates. Lastly, ground-based temperature measurements may help fill in data gaps found in the MODIS LST images.

4. Conclusions and Recommendations

Long-term evapotranspiration patterns can be used to detect the health of wetlands. The combined Simple Method and SSEB ET estimation model tested for use in restoration assessment of the Everglades of South Florida provided acceptable results under dry season conditions. On one hand, AET estimates provided by the model had good agreement with control eddy covariance based ET values during dry season months. For these dry months, the model proved to be both applicable and useful and provided AET values that may inform wetland recovery assessments. ET in wetlands is highest in these months due to high solar radiation, and wetland management and monitoring also are critical during this period. On the other hand, AET was underestimated for wet season months. The main source of error for wet month AET estimates came from poor LST data from the MODIS sensor due to prolonged periods of cloud cover.
The Simple Method approach provided acceptable results with good agreement with observed values during the critical dry season period, when cloud cover was low (rave(n = 59) = 0.7, pave < 0.0005), but requires further refinement to be viable for yearly estimates because of poor performance during wet season months, mainly because of cloud contamination. The model showed promise as a quick and simple monitoring tool for wetland recovery on an operational basis. Such products have been lacking to help evaluate the restoration of the Everglades. The simplicity of the model, requiring only temperature and solar radiation data, can produce results comparable to more complex methods when the input data are of good quality. Furthermore, this study demonstrated the model’s ability to successfully cover areas as large as the South Florida region. Weekly accurate estimates seem feasible for dry season months, when ET is highly dynamic spatiotemporally, and its estimation is very important.
Several aspects of the Simple Model/SSEB approach tested in this study can benefit from further refinement. First and foremost, better methods of gathering LST data are needed to replace data gaps during the cloudy wet season. Second, a larger network of solar radiation monitoring stations would help create more accurate PET maps for the South Florida region. Finally, ETf calculations may benefit from the introduction of new parameters (not just temperature) to increase the accuracy of final AET estimates.

Acknowledgments

The authors acknowledge the South Florida Water Management District and the USGS and NASA for the data used in this study. Melesse’s time was supported by the NASA-funded WaterSCAPES project. Participation by RM Price was supported by the Florida Coastal Everglades Long-Term Ecological Research program under National Science Foundation Grant No. DEB-1237517.

Author Contributions

Melesse and Price provided technical advice and reviewed several iterations of the paper for content and format accuracy. Dessu and Kandel provided guidance and resources during the data analysis portion of the study.

Conflict of Interest

The authors declare no conflicts of interest in this work.

References

  1. Maltby, E.; Barker, T. Section II: Wetlands in the natural environment, how do wetlands work? In The Wetlands Handbook; Maltby, E., Barker, T., Eds.; Wiley: Oxford, UK, 2009; Volume 2, pp. 115–326. [Google Scholar]
  2. Abers, J.S.; Pavri, S.; Aber, S.A. Part I and Part II. In Wetland Environments: A Global Perspective; Wiley-Blackwell: Chichester, UK, 2012; pp. 1–132. [Google Scholar]
  3. LePage, B.A. Wetlands: A multidisciplinary perspective. In Wetlands: Integrating Multidisciplinary Concepts, 1st ed.; Springer: New York, NY, USA, 2011; pp. 3–25. [Google Scholar]
  4. Abtew, W.; Melesse, A.M. Chapter 6: Evaporation and evapotranspiration estimation methods. In Evaporation and Evapotranspiration: Measurements and Estimations; Abtew, W., Melesse, A.M., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 63–91. [Google Scholar]
  5. Davis, D. Threats to Wetlands. Available online: http://permanent.access.gpo.gov/gpo701/threats.pdf (accessed on 18 September 2013).
  6. Mitsch, W.G.; Gosselink, J.G. The Wetland Environment. In Wetlands, 4th ed.; John Wiley & Sons: New York, NY, USA, 2000; pp. 107–258. [Google Scholar]
  7. Gurnell, A.M.; Hupp, C.R.; Gregory, S.V. Linking hydrology and ecology. Hydrol. Process. 2000, 14, 2813–2815. [Google Scholar] [CrossRef]
  8. Price, J.S.; Waddington, J.M. Advances in Canadian wetland hydrology and biogeochemistry. Hydrol. Process. 2000, 14, 1579–1589. [Google Scholar] [CrossRef]
  9. Janssen, R.; Goosen, H.; Verhoeven, M.L.; Verhoeven, J.T.A.; Omtzigt, A.Q.A.; Maltby, E. Decision support for integrated wetland management. Environ. Model. Softw. 2005, 20, 215–229. [Google Scholar] [CrossRef]
  10. Oberg, J.W.; Melesse, A.M. Wetland evapotranspiration dynamics vs. ecohydrological restoration: An energy balance and remote sensing approach. J. Am. Water Resourc. Assoc. 2005, 42, 565–582. [Google Scholar] [CrossRef]
  11. German, E.R. Regional Evaluation of Evapotranspiration in the Everglades; Water-Resources Investigations Report 00-4217; US Geological Survey: Tallahassee, FL, USA, 2000; p. 48. [Google Scholar]
  12. Monteith, J.L.; Unsworth, M.H. Principles of Environmental Physics, 2nd ed.; Butterworth-Heinemann: Woburn, MA, USA, 1990. [Google Scholar]
  13. Brooks, K.N.; Ffolliott, P.F.; Gregersen, H.M.; DeBano, H.F. Hydrology and the Management of Watersheds, 2nd ed.; Iowa State University Press: Ames, IA, USA, 1997. [Google Scholar]
  14. Tateishi, R.; Ahn, C.H. Mapping evapotranspiration and water balance for global land surfaces. ISPRS J. Photogramm. Remote Sens. 1996, 51, 209–215. [Google Scholar] [CrossRef]
  15. Mauser, W.; Schadlich, S. Modeling the spatial distribution of evapotranspiration on different scales using remote sensing data. J. Hydrol. 1998, 212–213, 250–267. [Google Scholar] [CrossRef]
  16. Melesse, A.; Nangia, V.; Wang, X.; McClain, M. Wetland restoration response analysis using MODIS and groundwater data. Sensors 2007, 7, 1916–1933. [Google Scholar] [CrossRef]
  17. Glenn, E.P.; Mexicano, L.; Garcia-Hernandez, J.; Naglerc, P.L.; Gomez-Sapiensa, M.M.; Tanga, D.; Lomelid, M.A.; Ramirez-Hernandezd, J.; Zamora-Arroyoe, F. Evapotranspiration and water balance of an anthropogenic coastal desert wetland: Responses to fire, inflows and salinities. Ecol. Eng. 2013, 59, 176–184. [Google Scholar] [CrossRef]
  18. Melesse, A.M.; Oberg, J.; Beeri, O.; Nangia, V.; Baumgartner, D. Spatiotemporal dynamics of evapotranspiration and vegetation at the glacial ridge prairie restoration. Hydrol. Process. 2006, 20, 1451–1464. [Google Scholar] [CrossRef]
  19. Zhao, X.; Liu, Y. Lake fluctuation effectively regulates wetland evapotranspiration: A case study of the largest freshwater lake in China. Water 2014, 6, 2482–2500. [Google Scholar] [CrossRef]
  20. Li, Z.; Liu, X.; Ma, T.; Kejia, D.; Zhou, Q.; Yao, B.; Niua, T. Retrieval of the surface evapotranspiration patterns in the alpine grassland-wetland ecosystem applying SEBAL model in the source region of the Yellow River, China. Ecol. Eng. 2013, 270, 64–75. [Google Scholar]
  21. Venturini, V.; Bisht, G.; Islam, S.; Jiang, L. Comparison of evaporative fractions estimated from AVHRR and MODIS sensors over South Florida. Remote Sens. Environ. 2004, 93, 77–86. [Google Scholar] [CrossRef]
  22. Jiang, L.; Islam, S. Estimation of surface evaporation map over southern great plains using remote sensing data. Water Resour. Res. 2001, 37, 329–340. [Google Scholar] [CrossRef]
  23. Jiang, L.; Islam, S.; Jutla, A.; Senarath, S.; Ramsey, B.H.; Eltahir, E. An intercomparison of regional latent heat flux estimation using remote sensing data. Int. J. Remote Sens. 2009, 24, 2221–2236. [Google Scholar] [CrossRef]
  24. Lagomasino, D.; Price, R.M.; Whitman, D.; Melesse, A.M.; Oberbauer, S. Spatial and temporal variability in spectral-based evapotranspiration measured from Landsat 5TM across two mangrove ecotones. Agric. For. Meteorol. 2014. [Google Scholar] [CrossRef]
  25. Senay, G.B.; Verdin, J.P.; Lietzow, R.; Melesse, A.M. Global daily reference evapotranspiration modeling and validation. J. Am. Water Resour. Assoc. 2008, 44, 969–979. [Google Scholar] [CrossRef]
  26. DBHYDRO. Available online: http://xportal.sfwmd.gov/dbhydroplsql/show_dbkey_info.main_menu (accessed on 15 March 2014).
  27. LP DAAC. Available online: https://lpdaac.usgs.gov/data_access (accessed on 10 February 2014).
  28. Toller, GN; Isaacman, A. MODIS Level 1B Product User’s Guide; NASA/Goddard Space Flight Center: Greenbelt, MD, USA, 2012; p. 56. [Google Scholar]
  29. Wan, Z. Collection-5 MODIS Land Surface Temperature Products User’s Guide; University of California: Santa Barbara, CA, USA, 2006. [Google Scholar]
  30. Ackerman, S.; Frey, R.; Strabala, K.; Liu, Y.; Gumley, L.; Baum, B.; Menzel, P. Discriminating Clear-Sky from Cloud with MODIS Algorithm Theoretical Basis Document (MOD35); Cooperative Institute for Meteorological Satellite Studies, University of Wisconsin-Madison: Madison, WI, USA, 2010; p. 20. [Google Scholar]
  31. Earth Explorer. Available online: http://earthexplorer.usgs.gov (accessed on 02 February 2014).
  32. Shoemaker, W.B.; Lopez, C.D.; Duever, M.J. Evapotranspiration over Spatially Extensive Plant Communities in the Big Cypress National Preserve, Southern Florida, 2007-2010; U.S. Geological Survey SIR 2011-5212; U.S. Geological Survey: Reston, VA, USA, 2011; p. 46. [Google Scholar]
  33. Abtew, W. Evapotranspiration measurements and modeling for three wetland systems in South Florida. J. Am. Water Resour. Assoc. 1996, 32, 465–473. [Google Scholar] [CrossRef]
  34. Senay, G.B.; Budde, M.; Verdin, J.P.; Melesse, A.M. A coupled remote sensing and simplified surface energy balance approach to estimate actual evapotranspiration from irrigated fields. Sensors 2007, 7, 979–1000. [Google Scholar] [CrossRef]
  35. Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL) 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
  36. Bastiaanssen, W.G.M.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.F.; Roerink, G.J.; van der Wal, T. A remote sensing Surface Energy Balance Algorithm for Land (SEBAL) 2. Validation. J. Hydrol. 1998, 212–213, 213–229. [Google Scholar] [CrossRef]
  37. Bastiaanssen, W.G.M.; Noordman, E.J.M.; Pelgrum, H.; Davids, G.; Thoreson, B.P.; Allen, R.G. SEBAL model with remotely sensed data to improve water-resources management under actual field conditions. J. Irrig. Drain. Eng. 2005, 131, 85–93. [Google Scholar] [CrossRef]
  38. Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational evapotranspiration mapping using remote sensing and weather datasets: A new parameterization for the SSEB approach. J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef]
  39. Pilz, J.; Spöck, G. Why do we need and how should we implement Bayesian Kriging methods. Stoch. Environ. Res. Risk Assess. 2007, 22, 621–632. [Google Scholar] [CrossRef]
  40. Abtew, W.; Obeysekera, J.; Irizarry-Ortiz, M.; Lyons, D.; Reardon, A. Evapotranspiration estimation for South Florida. In Proceedings of World Water and Environmental Resources Congress 2003, Philadelphia, PA, USA, 22–26 June 2003.
  41. Douglas, E.M.; Jacobs, J.M.; Sumner, D.M.; Ray, R.L. A comparison of models for estimating potential evapotranspiration for Florida land cover types. J. Hydrol. 2009, 373, 366–376. [Google Scholar] [CrossRef]
  42. Abtew, W. Comparison of Bowen Ratio Measurements and Model Estimations. In Evapotranspiration in the Everglades; South Florida Water Management District: West Palm Beach, FL, USA, 2004; pp. 2–13. [Google Scholar]
  43. Bidlake, W.R.; Woodham, W.M.; Lopez, M.A. Evapotranspiration from Areas of Native Vegetation in West-Central Florida; Water-Supply Paper 2430; U.S. Geological Survey: Washington, DC, USA, 1996. [Google Scholar]
  44. Mao, L.M.; Bergman, M.J.; Tai, C.C. Evapotranspiration measurement and estimation of three wetland environments in the Upper St. Johns River Basin, Florida. J. Am. Water Resour. Assoc. 2002, 38, 1271–1285. [Google Scholar] [CrossRef]
  45. Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef]
  46. Jiang, L.; Islam, S.; Guo, W.; Jutla, A.S.; Senarath, S.U.S.; Ramsay, B.H.; Eltahir, E. A satellite-based daily actual evapotranspiration estimation algorithm over South Florida. Glob. Planet. Chang. 2009, 67, 62–77. [Google Scholar] [CrossRef]
  47. Enku, T.; van der Tol, C.; Gieske, A.; Rientjes, T. Chapter 8: Evapotranspiration modeling using remote sensing and empirical models in the Fogera Floodplain. In Nile River Basin: Hydrology, Climate and Water Use; Melesse, A.M., Ed.; Springer: Dordrecht, The Netherlands, 2011; pp. 163–178. [Google Scholar]
  48. Courault, D.; Seguin, B.; Olioso, A. Review on estimation of evapotranpiration from remote sensing data: From empirical to numerical modeling approaches. Irrig. Drain. Syst. 2005, 19, 223–249. [Google Scholar] [CrossRef]
  49. Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.A. Landsat-based energy balance and evapotranspiration model in Western US water rights regulation and planning. Irrig. Drain. Syst. 2005, 19, 251–268. [Google Scholar] [CrossRef]
  50. Savoca, M.E.; Senay, G.B.; Maupin, M.A.; Kenny, J.F.; Perry, C.A. Actual Evapotranspiration Modeling Using Operational Simplified Surface Energy Balance (SSEBop) Approach; U.S. Geological Survey: Reston, VA, USA, 2013; p. 14. [Google Scholar]

Share and Cite

MDPI and ACS Style

Ceron, C.N.; Melesse, A.M.; Price, R.; Dessu, S.B.; Kandel, H.P. Operational Actual Wetland Evapotranspiration Estimation for South Florida Using MODIS Imagery. Remote Sens. 2015, 7, 3613-3632. https://doi.org/10.3390/rs70403613

AMA Style

Ceron CN, Melesse AM, Price R, Dessu SB, Kandel HP. Operational Actual Wetland Evapotranspiration Estimation for South Florida Using MODIS Imagery. Remote Sensing. 2015; 7(4):3613-3632. https://doi.org/10.3390/rs70403613

Chicago/Turabian Style

Ceron, Cristobal N., Assefa M. Melesse, René Price, Shimelis B. Dessu, and Hari P. Kandel. 2015. "Operational Actual Wetland Evapotranspiration Estimation for South Florida Using MODIS Imagery" Remote Sensing 7, no. 4: 3613-3632. https://doi.org/10.3390/rs70403613

APA Style

Ceron, C. N., Melesse, A. M., Price, R., Dessu, S. B., & Kandel, H. P. (2015). Operational Actual Wetland Evapotranspiration Estimation for South Florida Using MODIS Imagery. Remote Sensing, 7(4), 3613-3632. https://doi.org/10.3390/rs70403613

Article Metrics

Back to TopTop