1. Introduction
Suspended sediment concentration (SSC) is one of the critical parameters in the evaluations of ecological environment and water quality in the coastal zone [
1]. Traditional surveys of suspended sediment concentration mainly depend on observations in selected point locations from vessels moving in slow speed, and thus the process overall has low efficiency. Only temporally and spatially discrete data can be acquired. However, aerial and satellite remote sensing methods can be used to efficiently detect the SSC of waters over a relatively large area in real-time and possibly in a continuous manner. Therefore, remote sensing (RS) is an important means to monitor the ocean ecological environment on an extensive spatial scale [
2,
3,
4,
5,
6,
7,
8,
9].
The monitoring of SSC by RS techniques has a history of 3 to 4 decades, relatively recent as compared to the monitoring of water quality parameters using conventional techniques. RS data have been exploited to produce geographically extensive maps of SSC, including the use of AVHRR in the 80s [
7,
10], Landsat archive in the 70s [
8,
11,
12,
13,
14], SeaWiFS imagery after 1997 [
9], MERIS imagery after 2003 [
5,
6] and MODIS data from 2002 up to now [
15]. The amount of SSC data that can be retrieved from satellite imagery would be considerably larger than the historical records of SSC obtained by the traditional means. The key to retrieve SSC is to develop a quantitative model between the RS data and SSC. Remote sensing inversion models of SSC can be approximately classified into three categories. The first category are statistical models based on empirical relationships between optical properties and SSC [
16,
17]. These type of models are simple and easy to implement but lack physical foundation. The empirical relationships are more geographically specific and may not be applied to other areas [
18]. The second category are theoretical models that are based strictly on the radiative transfer theory to simulate the spectra at the top-of-atmosphere (TOA) with different SSC and atmospheric conditions [
19,
20,
21,
22]. However, these models require accurate profile information of the inherent optical properties (IOPs) of waters and atmosphere. The third are semi-analytical models based on the relationship between the IOPs of sea water and SSC [
23,
24,
25,
26]. As the semi-analytical models have higher inversion precision and universality as compared to the statistical models, and are more convenient and flexible than the theoretical models, they are the attractive means for SSC retrieval.
As early as 1993, Manikiam
et al. [
27] studied the absorption and scattering properties of suspended sediment in the west coast of India. They proposed a simple semi-analytical model for SSC retrieval based upon the radiative transfer theory. Nechad
et al. [
28] developed a suspended particulate matter (SPM) algorithm using the reflectance model, which was proposed by Park and Ruddick [
29], to take into account the bidirectional effects of turbid waters. The relative error in SPM estimation was less than 30% in the spectral range of 670–750 nm. A semi-analytical algorithm was proposed by Shen
et al. [
30] for SPM retrieval using five ocean-color sensors, which allowed for temporal gaps between sequential pairs of satellite images to be filled in. SPM products derived from three sensors with nearly synchronous transit (e.g., Envisat MERIS, Terra MODIS, and FY-3 MERSI) exhibited excellent accordance with mean differences of 0.056, 0.057 and 0.013 g·L
−1 for three fixed field stations, respectively, in the Yangtze estuary.
By analyzing the optical characteristics of waters, Doxaran
et al. [
31] pointed out that IOPs were the primary factors affecting the reflectance of waters. However, acquire
in situ IOPs data is very difficult and controlling the conditions of observation is quite complicated [
32,
33]. An indirect method to obtain IOPs is to retrieve them from remote sensing reflectance [
34]. Lee
et al. [
35] developed a semi-analytical model that applied total remote sensing reflectance to retrieve the absorption coefficient of waters, which was validated by the measurements obtained from the Gulf of Mexico and Monterey Bay. The total absorption coefficient inversion errors were 13.0%, 14.5%, 13.6% at 440 nm, 448 nm and 550 nm of wavelengths, respectively. Roesler and Perry [
36] further developed a semi-analytical algorithm for the retrieval of absorption and scattering coefficients of ocean optical components. The algorithm was tested using 35 reflectance spectral data obtained from irradiance measurements in diverse waters conditions (the concentration of chlorophyll-a ranged from 0.07 to 25.35 µg·L−1). The retrieval error for the absorption coefficient of phytoplankton was less than 35% in most marine environments (when the concentration of chlorophyll-a was below 3 µg·L−1) and the modeled particle backscattering coefficients were linearly correlated to total particles cross section over a twenty-fold range in backscattering coefficient. Hoge and Lyon developed a linear matrix algorithm, which used remote sensing reflectance (Rrs) at three bands (Rrs(410), Rrs(490), Rrs(555)), to retrieve the IOPs of in-water content. The method was first used to calculate 5 × 105 water-leaving spectral radiances for a wide range of normally distributed IOPs values. Then, the spectral radiances were inverted to simultaneously provide the IOPs values of in-water content on a pixel-by-pixel [
37,
38,
39]. Loisel and Stramski
et al. [
40,
41] proposed a semi-analytical method based on the radiative transfer theory. Specifically, they used the irradiance reflectivity R (
) and the average vertical attenuation coefficient K
d (within the first optical depth) just beneath the water surface to retrieve the total absorption, scattering and backscattering coefficients. The inversion results of the total absorption coefficient excluding pure water contribution, a
t and b
b were best in blue and green bands. Smyth
et al. [
34] developed a semi-analytical model to invert the IOPs through satellite or
in situ ocean color data. The model retrieved the total absorption and backscattering coefficients with an assumed spectral slope of the particles backscattering coefficient, b
bp, a
t, and the standard ratios of a
phy and a
dg (a
phy: Phytoplankton absorption, a
dg: Detritus and yellow substance (or gelbstoff) absorption). Compared with over 400
in situ data points, the model produces reasonably accurate retrievals for total absorption and backscatter across the entire spectrum, with regression slopes close to unity, indicating little or no bias, while the RMSE was higher in the logarithmic scale with a range of 0.189 to 0.270 at 412 nm and 555 nm, respectively.
The critical aspect in the semi-analytical models for SSC retrieval is to determine the relationship between SSC and the IOPs of waters. Recently, more research was carried out to study the relationships between IOPs and AOPs [
42,
43,
44,
45,
46,
47]. Among them, the quasi-analytical algorithm (QAA) for the inversion of IOPs developed by Lee
et al. [
48] based on the reflectance model of Gordon
et al. [
49] is one of more mature methods with efficient calculation. In the algorithm, only a few empirical relationships were needed [
48]. The reflectance model of Gordon
et al. [
49] used open sea waters and was validated for inland turbid waters by Dekker
et al. [
50]. It has been used intensively to retrieve SPM in estuarine, coastal and deep waters [
28]. The QAA has been used to invert the IOPs of waters off the Chinese coast, e.g., in the Yellow Sea by Hu
et al. [
51], and in the South Sea coastal area of Fujian by Wang
et al. [
52]. Nevertheless, further studies are needed to evaluate whether the QAA is generally applicable, especially in coastal regions such as the Gulf of Bohai, China, where large-scale constructions along the coast created varying ocean ecological environments.
The main objective of this study is to develop a semi-analytical model of remote sensing inversion of SSC for the Gulf of Bohai based on QAA. The algorithm was derived using the information gathered through field observations and from the spectral characteristics of waters in the study area. The semi-analytical model was compared to previous statistical models derived for the Gulf of Bohai, demonstrating its comparatively higher precision and universality. Using the model and TM data, SSC levels of the entire study region were estimated. These estimates can serve as the baseline for a future monitoring of the ocean environment in the Gulf of Bohai in a timely manner.
4. Conclusions
The Gulf of Bohai area is labeled as the top priority region of the circular economic development zone by the Chinese Government in the last ten years. Large-scale constructions cause significant changes in the ocean’s ecological environment. It is important to monitor the ocean’s ecological environment by quantitative remote sensing in a timely manner.
SSC is one of the critical parameters in ocean environmental evaluation. SSC levels in the Gulf of Bohai are relatively low, hence, an effective inversion model should have high sensitivity and stability. Existing models are mostly statistical models, based on the correlation between the apparent optical properties (remote sensing reflectance) and SSC levels. Because remote sensing reflectance is associated with the conditions of observation and the geographical scope of the waters, empirical statistical models are of limited applications. The semi-analytical model developed in this article, based on the QAA algorithm, investigated the relationship between IOPs of waters constitutes and remote sensing reflectance. Because IOPs are related to the inherent nature of waters and do not vary with the conditions of observation, the semi-analytical model showed a higher precision and universality than the empirical models.
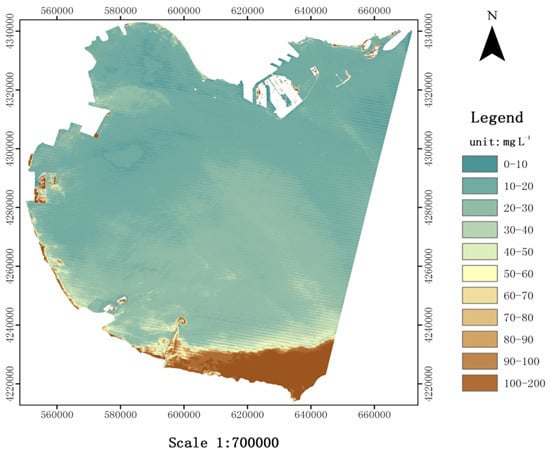
The study results indicated that the most sensitive band to SSC levels in the study area is the NIR band of Landsat5 TM images. This finding is consistent with the studies by Onderka
et al. [
13], Chen
et al. [
66] and Li
et al. [
67]. A quadratic polynomial semi-analytical model is proposed as an SSC retrieval model based on the relationship between the inherent optical properties and apparent optical properties of water using the QAA. According to 20 validation points, the accuracy of the model has an average relative error of 12.32% and the RMSE of 4.53 mg·L
−1 while the correlation coefficient between observed and estimated SSC is 0.95. Unlike the empirical statistical model that was developed using the same
in situ data, the semi-analytical model is more sensitive to the changes of the remote sensing reflectance. Compared with the previous statistical models used in other studies, the semi-analytical model that includes a relationship between reflectance, IOPs and SSC shows a slightly higher precision. Using the retrieval model and TM data, SSC levels of the entire study region were estimated. The distribution characteristics of SSC levels revealed the sources of sediment in the Gulf of Bohai which was carried by the Yellow River to the estuary in the southern part, re-suspended sediment in the shallow regions and due to the human activities effects along the coastal areas, especially in the nearby Huanghua Port. The study results can serve as the baseline for future monitoring of the ocean environment in the region.