Next Article in Journal
Mapping Aquatic Vegetation in a Large, Shallow Eutrophic Lake: A Frequency-Based Approach Using Multiple Years of MODIS Data
Next Article in Special Issue
To Fill or Not to Fill: Sensitivity Analysis of the Influence of Resolution and Hole Filling on Point Cloud Surface Modeling and Individual Rockfall Event Detection
Previous Article in Journal
Responses of Natural Vegetation Dynamics to Climate Drivers in China from 1982 to 2011
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 7
Issue 8
10.3390/rs70810269
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Does HDR Pre-Processing Improve the Accuracy of 3D Models Obtained by Means of two Conventional SfM-MVS Software Packages? The Case of the Corral del Veleta Rock Glacier

by
Álvaro Gómez-Gutiérrez
1,*,
José Juan De Sanjosé-Blasco
2,
Javier Lozano-Parra
1,
Fernando Berenguer-Sempere
3 and
Javier De Matías-Bejarano
2
1
GeoEnvironmental Research Group, University of Extremadura, Avda. De la Universidad s/n, 10071 Cáceres, Spain
2
Geomatics Engineering Research Group, University of Extremadura, Avda. De la Universidad s/n, 10071 Cáceres, Spain
3
San Antonio Catholic University of Murcia, Campus de los Jerónimos, s/n, 30107 Murcia, Spain
*
Author to whom correspondence should be addressed.
Remote Sens. 2015, 7(8), 10269-10294; https://doi.org/10.3390/rs70810269
Submission received: 25 May 2015 / Revised: 22 July 2015 / Accepted: 31 July 2015 / Published: 11 August 2015
(This article belongs to the Special Issue Use of LiDAR and 3D point clouds in Geohazards)
Browse Figures
Versions Notes

Abstract

:
The accuracy of different workflows using Structure-from-Motion and Multi-View-Stereo techniques (SfM-MVS) is tested. Twelve point clouds of the Corral del Veleta rock glacier, in Spain, were produced with two different software packages (123D Catch and Agisoft Photoscan), using Low Dynamic Range images and High Dynamic Range compositions (HDR) for three different years (2011, 2012 and 2014). The accuracy of the resulting point clouds was assessed using benchmark models acquired every year with a Terrestrial Laser Scanner. Three parameters were used to estimate the accuracy of each point cloud: the RMSE, the Cloud-to-Cloud distance (C2C) and the Multiscale-Model-to-Model comparison (M3C2). The M3C2 mean error ranged from 0.084 m (standard deviation of 0.403 m) to 1.451 m (standard deviation of 1.625 m). Agisoft Photoscan overcome 123D Catch, producing more accurate and denser point clouds in 11 out 12 cases, being this work, the first available comparison between both software packages in the literature. No significant improvement was observed using HDR pre-processing. To our knowledge, this is the first time that the geometrical accuracy of 3D models obtained using LDR and HDR compositions are compared. These findings may be of interest for researchers who wish to estimate geomorphic changes using SfM-MVS approaches.

Graphical Abstract

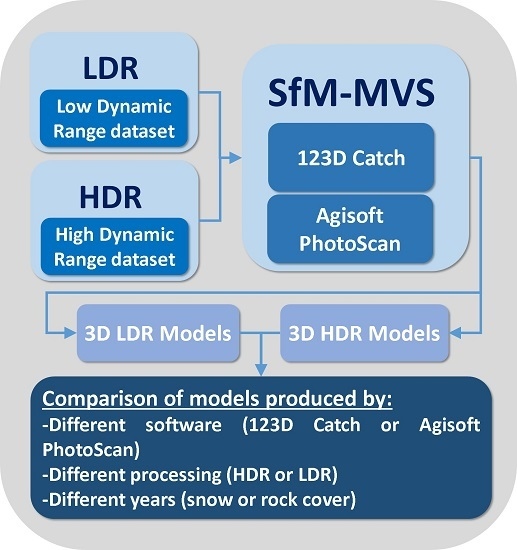
1. Introduction

Photographs have been widely used as documentary evidences in numerous fields of science since the invention of photography. In the case of Earth Sciences, photographs have been used to describe, analyze and quantify processes. Capturing photographs outdoor usually represents a challenge because light conditions cannot be controlled or programmed as in a laboratory experiment [1]. The capture of images with high differences in the illumination of the brightest and the darkest parts of the scene (i.e., scenes with High Dynamic Ranges or HDR) is not possible with conventional digital cameras available today. The dynamic range of an image can be defined as the ratio between areas with the highest and the lowest light intensity in the scene. In natural environments this figure can reach values around 500,000:1 [2]. The amount of light received by the sensor inside a digital camera is controlled by the exposure time, which is the time that the shutter of the camera is opened. High exposure times usually result in photographs with details and textures in areas with low illumination while high illuminated areas are usually shown in a uniform white colour without details. On the other hand, low exposure times result in photographs with details and textures in zones highly illuminated while areas with low illumination are shown like uniform black colored parts. Therefore, it is not always possible to capture photographs in natural environments without losing details and texture in bright and dark areas due to overexposure (long exposure times) and underexposure (short exposure times), respectively.
Since the 90s, HDR procedures have been developed and applied successfully to overcome this limitation. HDR techniques are based in the use of multiple images of the same scene that have been captured from the same location but with different exposure times known as Low Dynamic Range images (LDR). Then, LDR images are combined in a unique scene selecting the most appropriate illumination for each pixel in the set of LDR images. The result is a HDR composition showing details in high and low illuminated features in the scene. This result can be exported as a radiance or a tone map to be used as a conventional picture within any software.
In the past five years, automatic photogrammetric procedures based on Structure from Motion and Multi-View Stereo techniques (SfM-MVS) have been widely explored and applied in the field of Earth Sciences, particularly in Geomorphology [1,3,4,5,6,7,8,9,10]. The SfM [11] technique solves the camera parameters and orientations and produces a sparse 3D point cloud of the scene. These clouds are commonly insufficiently detailed and noisy [12] to be applied for geomorphological purposes. The MVS [13] approach reduces the noise in the scene and densify the point cloud getting the number of points in the cloud to increase by two or three orders of magnitude [3]. The advantages of SfM-MVS against other methods that offer similar accuracies have been highlighted by several researchers: accuracy, low cost and little expertise required as compared with more traditional techniques, [1,3,14]. The accuracy of SfM-MVS approaches depends on several factors: average distance from the camera to the target, camera network geometry and characteristics, quality and distribution of the ground control points, software and illumination conditions. The SfM-MVS approaches are currently implemented in a wide variety of software packages and web services (e.g., Agisoft Photoscan [15], Arc 3D [16], Bundler and PMVS2 [17], CMP SfM [18], Micmac [19], Photomodeler [20], Visual SfM [21], 123D Catch [22], etc.). Among these software packages Agisoft Photoscan (≈400 €) and 123D Catch (free available) are two interesting options. The 123D Catch software has been previously applied to estimate gully headcut erosion [1], to reconstruct riverbank topography [23], to generate Digital Elevation Models of a rock glacier [10] and to measure coastal changes [24]. Regarding Agisoft Photoscan, it has been previously used to estimate the mass balance of a small glacier [25] or to carry out a multi-temporal analysis of landslide dynamics [26]. Several works have tried to understand the relationship between the accuracy of SfM-MVS approaches and the different scales of work (plot, geomorphological feature, sub-basin, basin and landscape scale) [3,27]. Works analyzing the accuracy of a specific software are common, however researches comparing the performance of two or several packages, algorithms, workflows or pipelines applied to the same study area are scarce in the literature. [8] is a recent exception where Visual SfM [21] and Micmac [19] are compared and used to monitor the displacement of a slow-moving slope movement. A general opinion among the scientific community is that the validation of SfM-MVS techniques, approaches and pipelines is just beginning and more examples are required to understand the frontiers and limitations of these methods.
Some SfM-MVS approaches have been validated robustly in recent works [3,27], however most of the validations are carried out with gridded data, a result of processing the point clouds (which are the primary result of the SfM-MVS methods) and using conventional statistics as the Root Mean Square Error (RMSE) calculated using a few points in the cloud-model. The use of rasterized surfaces is justified because most of the final derived or secondary products obtained from SfM-MVS raw data are Digital Elevation Models (DEMs) and derived attributes as gridded surfaces. However, these surfaces bind together errors of the SfM-MVS and the rasterization procedures and make it difficult to isolate the magnitude of each factor. The use of DEMs (or gridded surfaces) is related with the traditional work of geomorphologists with Geographical Information Systems (GIS) in a not real 3D environment. SfM-MVS primary data are 3D point clouds and an algorithm performing a test of the quality of point clouds in 3D is necessary [14].
As stated before, in natural environments, shadows and materials with different illuminations are common and they cause errors or blind areas in the resulting photo-reconstructed 3D models. SfM-MVS software packages demand images with rich textures and poor textured scenes may produce outliers or large areas without data. The performance of SfM-MVS is based on identifying matching features in different images commonly using the Scale Invariant Feature Transform algorithm (SIFT) [28]. Then, the matching features are used to iteratively solve the camera model parameters. Therefore, the final quality of the 3D model depends, among other factors, on the image texture of the surfaces in the scene [29] because the matching algorithm works with image textures. Concurrently, image texture will depend on the complexity of the features, the lighting and the materials of every scene [5]. In the field of geomorphological research, this problem has been documented. For example, some recent works [1,5,30] showed problems in areas with dense and homogeneous vegetation cover and others [31] talked about surfaces with bare sand, snow or other highly flat surfaces as candidates for poor results using SfM-MVS. The relationship between the quality of a DEM obtained by means of photo-reconstruction methods and the amount of shadowed-lighted areas in the photographs used as input in the photo-reconstruction procedure has been recently showed by [10]. Additionally, the surficial cover of different geomorphological features can be highly variable in time. For instance, a riverbank can be bare, vegetated or covered by water in different times along the hydrological year. This variability results in quite different textures in the photographs and should be taken into account when estimating thresholds to quantify geomorphic changes. In the case of rock glaciers, strong changes in the light conditions and the materials covering the ice are experienced along the year. In this kind of geomorphological feature, debris or rocks cover the ice forming the glacier permanently. At the same time, this layer of rocks may be partially or totally covered by snow during a part of the year. Although the use of HDR techniques seems to be appropriate to improve the performance of SfM-MVS approaches, this hypothesis has not been tested yet [32]. Point clouds obtained with HDR and LDR images were compared [33] but authors did not use any benchmark model to estimate the degree of improvement, if any. They concluded that, geometrically, both point clouds were similar, although a visual qualitative enhancement of the contrast in the colour of the point cloud was observed. Other recent work tested whether the pre-processing of digital images with HDR techniques may improve 3D models of cultural heritage objects obtained by means of SfM-MVS techniques [32]. Authors showed that point clouds generated using HDR compositions yielded 5% more points matched than point clouds obtained using LDR images for a ceramic object [32]. In the case of a metallic object, the increase in the number of points matched was higher with 63% more than the point clouds generated using LDR images as input. In this work, authors did not test the geometrical accuracy of the point clouds generated using HDR compositions [32]. Also recently, classical digital photogrammetry was fed with HDR images [34] and later applied to measure geometry and light simultaneously in roadways [35]. The results proved the usefulness of HDR approaches within the classical digital photogrammetry pipeline.
Therefore, the main objective of this work is to investigate the accuracy that can be obtained from different workflows for the 3D photo-reconstruction of the Corral del Veleta rock Glacier in Spain in three different years: 2011, 2012 and 2014. Specifically, the following issues were analyzed:
-
The possibility of improving SfM-MVS techniques with the use of HDR tone mapped images.
-
The accuracy of two different software packages commonly used to get 3D models of geomorphological features: 123D Catch [22] and Agisoft Photoscan [15].
-
The influence of snow or debris cover in the accuracy of the resulting photo-reconstructions for the Corral del Veleta rock glacier.
The estimation of the accuracy of the point clouds will be carried out using traditional parameters, such as the RMSE, but also more specific and recently proposed 3D distance tests.

2. Study Area, Material and Methods

2.1. Study Area

The study was carried out in the Corral del Veleta rock glacier in Sierra Nevada mountainous range (Figure 1A: SE, Spain: 37º3ʹN, 3º21ʹW). Numerous research works have been published about the Corral del Veleta rock glacier and rock glaciers in the Sierra Nevada mountainous system during the last years (e.g., [36,37]). Therefore, only a brief explanation about the main characteristics of the study area are presented here and the interested reader is referred to [36,37] for further information.
Remotesensing 07 10269 g001 1024
Figure 1. (A) Location of the study area in the Iberian Peninsula and (B) Orthophotograph of the study area that includes the extension of the Corral del Veleta rock glacier, the crest of the ancient lateral moraine, the border of the Veleta Cirque and the Veleta Peak (3398 m.a.s.l.). Additionally, camera locations, control points, Terrestrial Laser Scanner (TLS) and total station sites are shown in (B).
Figure 1. (A) Location of the study area in the Iberian Peninsula and (B) Orthophotograph of the study area that includes the extension of the Corral del Veleta rock glacier, the crest of the ancient lateral moraine, the border of the Veleta Cirque and the Veleta Peak (3398 m.a.s.l.). Additionally, camera locations, control points, Terrestrial Laser Scanner (TLS) and total station sites are shown in (B).
Remotesensing 07 10269 g001
The Veleta rock glacier is located in the Corral del Veleta Cirque (Figure 1B) which was the source of a white glacier during the last glaciation [36]. In the Little Ice Age, a small glacier is sheltered in the upper part of the cirque, originating a small fossil ice body, which nowadays is under a detritic cover. The Veleta rock glacier is the southernmost rock glacier in Europe, and is assumed as a key indicator about the effects of climate change in the Mediterranean region and high mountain areas within this region [36]. A recent work has shown the steadily decline of the ice body as a consequence of recent climatic conditions that are unfavorable to the presence of snow over the rock debris in summer time [36].
The glacier presents an average altitude of the detritic surficial body of 3,106 m.a.s.l. and is formed by heterometric blocks of feldespathic micaschist, varying in size from several m3 to cm3 and includes a coarse matrix mixed with an internal fine matrix. The surficial projection of the ice extents 3815 m2 with a total length of 130 m and an average width of 38 m. Geophysical prospections have estimated the average thickness of the ice body in 8.0 m.

2.2. Capture of the Photographs

The acquisition of photographs in the study area represents a challenge because of the restrictions for camera locations due to the steep relief but also because of the conditions of high mountain environments (weather, unreachable areas, etc.). At the same time, the glacier surface is also challenging because of its high roughness and complexity. The photographs were taken from the top of the Veleta peak (3398 m.a.s.l.) focusing on the glacier and getting a near vertical view of the Corral del Veleta cirque (Figure 2A). The distance from the peak to the glacier is approximately 300 m (Figure 2A). The geometry of the pose is constrained to a few locations in the top of the wall of the Corral del Veleta because the whole glacier is not visible from other locations and the distance from the camera to the target is determined by the height of the wall. The ideal design of the capture would be a network of convergent photographs framing the whole glacier and acquired from the limits of the study area focusing in the centre of the glacier. In high mountain environments, the camera locations are usually limited to a few sites and the estimation of errors-accuracies under these conditions may be of interest for researchers concerned in monitoring geomorphological features in areas with complex rough topography. Three photographic terrestrial surveys were carried out during the summer (august) of three different years (2011, 2012 and 2014). In 2011, the glacier was almost completely covered by a snow layer while in 2012 and 2014 only a few areas had a thin film of snow. The photographs were acquired with an uncalibrated Canon EOS 5D SLR camera attached to a pole and controlled by a remote shutter, using a fixed focal length of 100 mm provided by a Canon EF lens (EF100mm f/2.8 Macro USM). The rest of the parameters of the capture (i.e., shutter speed, ISO and aperture) were determined automatically by the sensor of the camera during each field survey. The resulting RAW images extended 4386 × 2920 pixels. Three photographs were capture from each camera location with Exposition Values (EV) of −1.00, 0.00 and +1.00 in order to get the HDR tone mapped images later. Nine camera locations were established in every survey (Figure 1B). These places are the only locations that allow a vertical perspective of the whole glacier along the top of the Veleta Cirque (Figure 1B). A deeper explanation about the capture of the photographs and the material and methods can be found in [38] and [10].
Remotesensing 07 10269 g002 1024
Figure 2. (A) View of the glacier from the top of the Corral del Veleta wall, (B) detail of the capture where the constrains for camera locations can be observed, (C) detail of a control point and (D) oblique photograph showing the front of the glacier and the steep relief and rough topography in the surroundings. Note that it is not possible to capture an oblique photograph of the whole glacier in the surroundings.
Figure 2. (A) View of the glacier from the top of the Corral del Veleta wall, (B) detail of the capture where the constrains for camera locations can be observed, (C) detail of a control point and (D) oblique photograph showing the front of the glacier and the steep relief and rough topography in the surroundings. Note that it is not possible to capture an oblique photograph of the whole glacier in the surroundings.
Remotesensing 07 10269 g002

2.3. Pre-Processing the Photographs

The pre-processing of the images was carried out with Fusion F.1 software, which is freely available in [39]. Firstly, pictures captured from the same location but with different EV were aligned to reduce noise artifacts in the final composition. Secondly, the HDR composition was elaborated by means of a local non-linear operator and the tone-mapping algorithm. Finally, each HDR composition was exported as a conventional image. Pre-processed HDR images and non-processed photographs (i.e., LDR images with EV = 0.00) were used as input in two different photo-reconstruction software packages: 123D Catch [22] and Agisoft Photoscan [15]. Figure 3 shows a summary of the pipelines. The 123D Catch software is free available and can be used as an on-line service or a conventional desktop software. Agisoft PhotoScan Profesional Edition is probably the most used commercial software that produces 3D models from photographs using SfM-MVS techniques. For both programs, parameters were set to get the maximum quality in the resulting point clouds. The 3D models were exported as .OBJ files from 123D Catch and as .LAS files from Agisoft Photoscan and imported within CloudCompare [40] to be scaled, referenced and compared with models acquired by means of a Terrestrial Laser Scanner.
Remotesensing 07 10269 g003 1024
Figure 3. Workflow diagram. EV is Exposition Value, LDR is Low Dynamic Range, HDR is High Dynamic Range and SfM-MVS is Structure-from-Motion Multi-View-Stereo.
Figure 3. Workflow diagram. EV is Exposition Value, LDR is Low Dynamic Range, HDR is High Dynamic Range and SfM-MVS is Structure-from-Motion Multi-View-Stereo.
Remotesensing 07 10269 g003

2.4. Processing the Point Clouds

Using permanent fixed stakes placed in the ancient lateral moraine of the glacier (i.e., stable area, Figure 1B) a local coordinate system was established and coordinates of 10 artificial targets inserted in the study area were measured (Figure 1B) with a total station during each field survey. These control points were used to reference and scale each point cloud generated by 123D Catch and Agisoft Photoscan. A classical 3D rigid transformation was used for this purpose including, therefore, three rotations, three translations and one scale factor. The benchmark models were acquired by means of a TLS and were also referenced into this local coordinate system. Four stations with the TLS device were located during every field survey in order to minimize the hidden areas (Figure 1B). The Scanstation C10 device by Leica was used for this purpose. The RMSEs obtained during the referencing of the TLS point clouds were always below 0.01 m.
After the referencing, each point cloud was masked to the same extension in order to allow comparison between the number of points, point density and distance to the reference cloud obtained by every methodological approach (LDR versus HDR), software (Agisoft Photoscan versus 123D Catch) and year (2011, 2012 and 2014).
The accuracy of the resulting point clouds was assessed by three different approaches. The first one is based on the analysis of the RMSEs obtained during the referencing procedure and using the targets and their coordinates measured by the total station. Once the point cloud is referenced, the Cloud-to-Cloud (C2C) [41] and the Multiscale Model to Model Comparison (M3C2) [14] methods were used. The C2C method provides accurate distance measurements between two point clouds when both clouds overlap in the study area [14]. The C2C approach has been previously used by different authors to test the accuracy of point clouds obtained by photo-reconstruction methods using clouds derived by TLS devices as benchmark [1,10]. However, the distance estimated by the C2C method is sensitive to outliers and the cloud’s roughness [14]. The average C2C distance between each point cloud and the benchmark model produced by the TLS was calculated with CloudCompare [40] software and used as an indicator of the quality of the point cloud.
The M3C2 method has been recently proposed by [14] because it does not need to interpolate any surface and calculates normals for each point considering a neighborhood of a pre-defined dimension. The M3C2 is specially designed for estimating the uncertainty of changes in rough complex topographies [14]. For this reason, the M3C2 is accepted to be the most adequate descriptor of the quality of a point cloud in a real 3D environment, especially in the case of complex geomorphological features, such as the Corral del Veleta rock glacier. Although the algorithm is originally designed to quantify geomorphological changes due to erosion, deposition, bank failures, landslides, etc. it can be also used to assess the accuracy of a point cloud regarding a reference or benchmark model. Assuming that two point clouds (PC1 and PC2) have been acquired simultaneously and one of them works as a benchmark cloud (PC1), distances estimated between them by the M3C2 algorithm are a measure of the PC2’s accuracy. The M3C2 was calculated using the plug-in implemented in CloudCompare software. The interested reader is referred to [14] for a deeper explanation about the performance of M3C2.
The C2C and the M3C2 methods provide the distance from each point in the cloud to the benchmark model. Using these distances, the absolute average distance for every point cloud has been calculated in order to avoid the compensation of positive and negative distances (i.e., points above and below the benchmark model in the case of the M3C2). Hence, the RMSE and the average absolute distances estimated by the C2C and the M3C2 methods were used as accuracy indicators here. The C2C and M3C2 present a more realistic measure of the distance between the point clouds and the benchmark dataset than 2.5D or DEM-based approaches. Commonly, gridded surfaces obtained from the superimposition of a 2.5D grid over the point cloud are used to estimate the accuracy of the techniques used to produce the point clouds. The 2.5D models are characterized by yielding only one Z coordinate for every XY-cell or planimetric location. During the transformation from the point cloud 3D coordinates to the gridded surface important errors may take place, driving the analysis to a non-realistic estimation of the accuracy.

3. Results and Discussion

A total of 12 point clouds were produced by the SfM-MVS approaches, four each year of the study (2011, 2012 and 2014). Additionally, one point cloud was acquired by means of the TLS every year. Figure 4 presents the photo-reconstructions of the glacier obtained with different pipelines for the years 2011 and 2014. Visually, important differences were observed between the point clouds generated with HDR and LDR images for the year 2011 (Figure 4A–D), under snow cover conditions. In 2014, the resulting point clouds did not present important differences from a visual viewpoint (Figure 4E–H) showing the debris cover of the glacier. Volumetric point densities for point clouds obtained by means of 123D Catch software were in the range of 1–100 points·m−3 while clouds elaborated with Agisoft Photoscan median point densities varied from 1500 to 2000 points·m−3.
Remotesensing 07 10269 g004 1024
Figure 4. Resulting point clouds obtained with (A) Low Dynamic Range (LDR) images in Agisoft Photoscan for the year 2011, (B) LDR images in 123D Catch for the year 2011, (C) High Dynamic Range (HDR) images in Agisoft Photoscan for the year 2011, (D) HDR images in 123D Catch for the year 2011, (E) LDR images in Agisoft Photoscan for the year 2014, (F) LDR images in 123D Catch for the year 2014, (G) HDR images in Agisoft Photoscan for the year 2014 and (H) HDR images in 123D Catch for the year 2014.
Figure 4. Resulting point clouds obtained with (A) Low Dynamic Range (LDR) images in Agisoft Photoscan for the year 2011, (B) LDR images in 123D Catch for the year 2011, (C) High Dynamic Range (HDR) images in Agisoft Photoscan for the year 2011, (D) HDR images in 123D Catch for the year 2011, (E) LDR images in Agisoft Photoscan for the year 2014, (F) LDR images in 123D Catch for the year 2014, (G) HDR images in Agisoft Photoscan for the year 2014 and (H) HDR images in 123D Catch for the year 2014.
Remotesensing 07 10269 g004
Table 1 presents the camera calibration parameters and their adjusted values for the models produced by Agisoft Photoscan as 123D Catch software does not generate this information. Agisoft Photoscan produces a figure with the spatial distribution of image residuals, however, you can only get this information if the scaling and georeferencing of the model has been carried out within the software. In order to keep a methodological consistency to compare Agisoft Photoscan and 123D Catch the scaling and georeferencing was carried out using CloudCompare software.
Table
Table 1. Camera calibration parameters with their initial and adjusted values, where fx and fy are horizontal and vertical focal length (in pixels) respectively, cx and cy are the x and y coordinates of the principal point and k1, k2 and k3 are the radial distortion coefficients. The Skew and tangential distortion coefficients (p1 and p2) were set to 0 in the initial and the adjusted calibration model. Pixel size of 0.008 mm, focal length of 100 mm and the size of the picture (4386 × 2920 pixels) were constant values for all the surveys. Note that these parameters are only estimated for the point clouds obtained by means of Agisoft Photoscan (123D Catch does not produce this information) and the spatial distribution of image residuals report, which is typically produced by this software, is not available since the scaling and referencing was carried out using CloudCompare software.
Table 1. Camera calibration parameters with their initial and adjusted values, where fx and fy are horizontal and vertical focal length (in pixels) respectively, cx and cy are the x and y coordinates of the principal point and k1, k2 and k3 are the radial distortion coefficients. The Skew and tangential distortion coefficients (p1 and p2) were set to 0 in the initial and the adjusted calibration model. Pixel size of 0.008 mm, focal length of 100 mm and the size of the picture (4386 × 2920 pixels) were constant values for all the surveys. Note that these parameters are only estimated for the point clouds obtained by means of Agisoft Photoscan (123D Catch does not produce this information) and the spatial distribution of image residuals report, which is typically produced by this software, is not available since the scaling and referencing was carried out using CloudCompare software.
LDR HDR
InitialAdjustResidual InitialAdjustResidual
2011fx12161.812053.9107.9 12161.811996.2165.6
fy12161.812053.9107.9 12161.811996.2165.6
cx2184.002176.667.34 2193.002144.2048.80
cy1456.001382.0673.94 1460.001451.368.64
k10.0000−0.18020.1802 0.0000−0.17830.1783
k20.00001.0894−1.0894 0.00000.7387−0.7387
k30.0000−2.88292.8829 0.0000−2.34322.3432
2012fx12161.812065.596.3 12161.812069.792.1
fy12161.812065.596.3 12161.812069.792.1
cx2184.002195.18−11.18 2193.002204.01−11.01
cy1456.001380.7175.29 1460.001388.5171.49
k10.0000−0.14980.1498 0.0000−0.15450.1545
k20.0000−0.10010.1001 0.00000.2562−0.2562
k30.000014.5264−14.5264 0.0000−0.15450.1545
2014fx12161.812022.5139.3 12161.812030.5131.3
fy12161.812022.5139.3 12161.812030.5131.3
cx2184.002170.6713.33 2193.002175.7717.23
cy1456.001426.2329.77 1460.001433.2426.76
k10.0000−0.15480.1548 0.0000−0.14720.1472
k20.00000.3270−0.3270 0.00000.0599−0.0599
k30.00008.1385−8.1385 0.000010.5228−10.5228

3.1. Global Structural Accuracy of the Point Clouds

The sources of error, and therefore inaccuracies, of the workflows presented in this work are mainly related to the following factors: the distance from the camera to the target [3], the geometry of the capture [25], the quality of the control points [25] and the modelling procedure that is influenced by cover type and illumination conditions [10,29]. The distance from the camera to the target and the geometry of the capture are, in this case, imposed by the steep relief and will be discussed later using the survey range or the relative precision ratio figures. An assessment of the sources of error is discussed in the following sections where the values of the RMSE, C2C and M3C2 are presented. The consistency in the use of instruments, techniques and methods allows the analysis of the effect of the HDR pre-processing, the use of different software and the influence of different cover types.
The quality of the control points (Figure 2C) is mainly controlled by their spatial distribution and the characteristics of the instruments used for their measurement. Figure 1B and Figure 5A show the spatial distribution of the 10 control points over the glacier covering the front, the sites and the head. The measurement of their coordinates was carried out with a laser total station that ensures an accuracy <0.5 cm in every single point.
Remotesensing 07 10269 g005 1024
Figure 5. (A) Oblique Low Dynamic Range conventional image (LDR) and (B) oblique High Dynamic Range composition (HDR, i.e., elaborated with three conventional photographs acquired with Exposition Values of −1.00, 0.00 and +1.00) of the Corral del Veleta rock glacier in 2011. Control points can be observed in red and yellow color for both images. Note that these photographs are not orthorectified and referenced so only an approximate reference distance is shown in the figure.
Figure 5. (A) Oblique Low Dynamic Range conventional image (LDR) and (B) oblique High Dynamic Range composition (HDR, i.e., elaborated with three conventional photographs acquired with Exposition Values of −1.00, 0.00 and +1.00) of the Corral del Veleta rock glacier in 2011. Control points can be observed in red and yellow color for both images. Note that these photographs are not orthorectified and referenced so only an approximate reference distance is shown in the figure.
Remotesensing 07 10269 g005
Scaling and referencing errors quantified by the RMSE reflect how the resulting models fit to the relative coordinate system established by the control points and measured by means of the total station, i.e., they are indicators of the global geometrical quality of the 3D model. If the control points present a good spatial distribution over the study area, the RMSE shows the global structural quality of the 3D model produced by the photo-reconstruction and can be an indicator of the presence of non-linear deformations. The RMSEs presented in Table 2 show that the best performance was always produced by Agisoft Photoscan and in two out of three cases using as input conventional LDR images (acquired with EV = 0.00). On the other hand, the worst performance was produced by 123D Catch software using as input HDR compositions. The RMSEs for the different workflows ranged from 0.036 m (Agisoft Photoscan software with LDR images in 2011) to 2.469 m (123D Catch software with HDR images in 2012).
The average RMSEs for the years 2014 and 2012, were lower and slightly lower (respectively) as compared to the average RMSE for the year 2011 (Table 2), when almost all the study area was covered by snow (Figure 4). The residuals of the camera calibration parameters presented in Table 1 also support this fact, however no statistical significant relationship was observed between the RMSE and the residuals of the different camera calibration parameters. Although the HDR pre-processing resulted in images with richer textures and a clear visual improvement of the features shown in the scene for the year 2011 (Figure 5), no significant improvement was found out in the RMSE using this approach. This qualitative visual improvement has been observed by [32,33].
Table
Table 2. Root Mean Square Errors (RMSEs; in meters) obtained during the scaling and referencing of each point cloud.
Table 2. Root Mean Square Errors (RMSEs; in meters) obtained during the scaling and referencing of each point cloud.
Software201120122014Average
Low Dynamic Range (LDR conventional) images123D Catch1.1280.4610.7911.027
Agisoft Photoscan0.0360.3410.2610.213
High Dynamic Range (HDR) images123D Catch2.3742.4691.0671.978
Agisoft Photoscan0.0670.3070.3910.242
Average 0.9020.8940.628
The figures presented in Table 2 result in an average ratio between RMSE and survey range of 1:370. In [27], a brief summary of previous works that have estimated this parameter resulted in a median ratio between RMSE and survey range of 1:639. A previous work in the Corral del Veleta rock glacier [10] presented values ranging from 1:1,071 to 1,429 but these values were calculated using the average C2C distance to the benchmark TLS model instead of using the RMSE and different pipelines. The dataset of RMSEs presented in Table 2 add knowledge to the needed systematic validation of SfM-MVS in a wide variety of environments demanded by the scientific community [27]. Although, it should be noted that the accuracies presented here could be improved because in this case the geometry of the pose is highly limited to a few locations in the top of the Corral del Veleta wall and the important differences in the survey range from 1:370 to the average figure of 1:639 for geomorphological features defined by [27] can be attributed to this weak geometry of the camera locations. According to this figures, the weak imposed geometry of the capture would be reducing in a half the expected accuracy of the models in the case of the Veleta rock glacier. For sure, other factors are influencing the difference in the average survey range for geomorphological features presented in [27] and the one estimated here, but it is hypothesized that an important increase in the accuracy of the models would be get with a convergent geometry of the pose. Camera network geometry has been recently supported as the main factor determining the quality of 3D models of a rock glacier by means of SfM-MVS techniques [25]. [10] validated two SfM-MVS approaches (a self-implemented algorithm and 123D Catch software) for the Corral del Veleta rock glacier finding out that only changes at sub-meter scale could be identified in a multi-temporal study according to the obtained differences with a TLS point cloud. The values of the RMSEs estimated here and presented in Table 2 suggest that only relatively large changes (>0.30 m) at medium-term time-scale (from 5 to 10 years at least) can be detected with the best resulting pipeline tested in this work (i.e., LDR images processed with Agisoft Photoscan software). [27] suggest that accuracies around 0.1 m can be reached from a 50 m survey range, however, in the case of the Corral del Veleta rock glacier the survey range is imposed by the relief to an approximate distance of 300 m from the Veleta Peak (3398 m.a.s.l.). The capture of oblique photographs at a lower height with an Unmanned Aerial Vehicle (UAV) would be a good option; however, usual weather conditions with variable high-speed gusts of wind make it almost impossible. On the other hand, it is not possible to take ground-based oblique photographs around the glacier because of the highly rough surface covered by blocks that results in large hidden areas from each perspective.

3.2. Average Local Accuracy of Each Point Cloud

Accuracies estimated for every point cloud in a 3D environment using C2C and M3C2 methods varied from 0.084 m to 1.679 m for the point clouds obtained by Agisoft Photoscan and LDR images in 2012 and the point clouds obtained by 123D Catch and HDR images in 2011 (Table 3). The M3C2 method has been recently proposed as the best way to compare 3D datasets for complex geomorphological features [14]. In the present study, M3C2 and C2C presented similar results being correlated with a coefficient R of 0.895 with p < 0.05 (Figure 6A). The Corral del Veleta rock glacier presents a special challenge for the C2C algorithm because of the complex and rough surface. Previous works have pointed out that the C2C algorithm is highly sensitive to outliers and the cloud’s roughness [14]. However, results obtained here showed a similar behavior in the C2C and M3C2 estimations.
On the other hand, the correlation analysis between the 3D more intensive methods (i.e., estimations based on the analysis of the whole cloud with the C2C and the M3C2) and the RMSE (Figure 6B) resulted in a coefficient R = 0.504 with p = 0.095 (correlation between C2C and RMSE) and R = 0.171 with p = 0.596 (correlation between M3C2 and RMSE). These results point out that although RMSE shows the global quality and fit of the structure of the model it is not necessary related to the average local accuracy of every single point in the cloud. Therefore, the RMSE by itself is not working here as a proper descriptor of the quality of the 3D models like it was showed years ago for 2.5D models within GIS environments (i.e., DEMs) [42]. Consequently, an analysis based on both kind of parameters, RMSE and C2C/M3C2, is recommended in order to check the lack of non-linear deformations, to estimate the global quality of the 3D model and to quantify the average local or detailed accuracy of the cloud. It should be noted that SfM-MVS approaches work matching features using their texture and illumination conditions, and control points are, usually, artificial features in the scene that have been marked to be clearly visible in the final model. Therefore, any statistic based on these artificial points may be not actually representing the error in the natural points included in the scene. An optional solution to mitigate this effect is to produce the 3D model first and, identify natural points in the 3D scene that can be measured in the field later [31].
Remotesensing 07 10269 g006 1024
Figure 6. Correlation between the Cloud-to-Cloud (C2C) and the Multiscale Model-to-Model (M3C2) (A) and between the C2C and the M3C2 with the RMSE (B).
Figure 6. Correlation between the Cloud-to-Cloud (C2C) and the Multiscale Model-to-Model (M3C2) (A) and between the C2C and the M3C2 with the RMSE (B).
Remotesensing 07 10269 g006
Alternatively, estimations of the quality of the model designed in a 3D environment (such as C2C and M3C2) are highly recommended against more traditional methods commonly used, that are based on gridding the 3D model and using a DEM of Differences approach (DoD) [43]. This strategy includes errors added during the gridding of the point cloud that can result in an imprecise estimation of the accuracy. Errors associated with the gridding procedure can be interpolation errors or errors derived from the optimal selection of the Z coordinate. For example, and also in the case of the Corral del Veleta rock glacier, [10] estimated the average absolute difference between two DEMs in 0.51 m: where the first DEM, was the result of rasterizing a point cloud produced by 123D Catch and the second DEM, worked as benchmark dataset and was obtained rasterizing a point cloud acquired by a TLS. However, the comparison of the two point clouds based on the C2C resulted in an average distance of 0.21 m. Therefore, whether the final aim of the analysis is the quantification of geomorphic change, the approach based on 2.5D surfaces may be estimating inaccurately the threshold to identify the real change. Additionally, some researchers have pointed out the unsuitability of tools currently implemented in GIS software packages to manage large 3D files and point clouds [5]. Other authors have argued that DEMs are the final product of SfM approaches and the errors estimated using raster-based comparisons are more representative of the real final accuracy [27].
Table
Table 3. Average absolute distances (AAD) between each point cloud and the benchmark model (acquired with a Terrestrial Laser Scanner). Distances were estimated by means of the Cloud-to-Cloud (C2C) [41] and the Multiscale Model-to-Model (M3C2) [14] methods and are presented in meters. Additionally, the median and the 90 percentile (P90) of the AAD for the M3C2 method are presented. Note that the average distances are obtained averaging the value of the C2C or M3C2 for every point in every cloud.
Table 3. Average absolute distances (AAD) between each point cloud and the benchmark model (acquired with a Terrestrial Laser Scanner). Distances were estimated by means of the Cloud-to-Cloud (C2C) [41] and the Multiscale Model-to-Model (M3C2) [14] methods and are presented in meters. Additionally, the median and the 90 percentile (P90) of the AAD for the M3C2 method are presented. Note that the average distances are obtained averaging the value of the C2C or M3C2 for every point in every cloud.
Low Dynamic RangeHigh Dynamic Range
123D CatchAgisoft Photoscan123D CatchAgisoft Photoscan
2011-C2C (AAD, meters)1.2660.9901.6790.926
-M3C2 (AAD, meters)1.0290.9161.4321.451
-M3C2 median (meters)0.7050.3910.7710.306
-M3C2 P90 (meters)2.3272.5513.7453.551
2012-C2C (AAD, meters)0.1800.1210.6970.123
-M3C2 (AAD, meters)0.1570.0840.1710.141
-M3C2 median (meters)0.1140.0720.0710.067
-M3C2 P90 (meters)0.3450.2220.2770.217
2014-C2C (AAD, meters)0.2070.1190.2170.105
-M3C2 (AAD, meters)0.2610.1510.2610.147
-M3C2 median (meters)0.1800.0860.1830.079
-M3C2 P90 (meters)0.5530.2910.7430.253
The geometry of the camera pose during the capture has been pointed out as the source of systematic errors in 3D models obtained by means of SfM-MVS techniques [44]. This is especially evident in the case of photographs acquired by Unmanned Aerial Vehicles (UAV), which produced multi-image networks with near parallel viewing directions [44] resulting in dome-type systematic errors. In the previous section, it was hypothesized that the global accuracy of the models could be notably improved using a convergent geometry during the capture according to the differences between the average survey range figures estimated for geomorphological features [27] and the survey range obtained here. The camera network geometry can also influence the existence of systematic errors in the resulting point clouds. In this work, camera locations are highly limited by the relief (Figure 2 and Figure 1B) and the existence of systematic errors was evaluated analyzing the spatial distribution of M3C2 distances (Figure 7) and visualizing gradient maps. Figure 7 shows the lower distances between the TLS benchmark model and the point cloud produced by Agisoft Photoscan with LDR images for the year 2014 (i.e., <−0.40) in the head of the glacier which is located in the limits of the study area and is the unique zone in 2014 that presents a thin film of snow. Probably, this fact is due to the presence of the small remain of snow because no other border effects or dome-type errors were found. Regarding the highest positives distances (i.e., >0.40) they are usually located in hidden areas under debris blocks that are not clearly visible in all the photographs. Therefore, no systematic error was found in the 3D models with this approach.
Remotesensing 07 10269 g007 1024
Figure 7. Three dimensional view of the spatial distribution of the Multiscale Model-to-Model (M3C2) distances between the benchmark Terrestrial Laser Scanner (TLS) 3D model and the point cloud produced by Agisoft Photoscan with Low Dynamic Range (LDR) images for the year 2014.
Figure 7. Three dimensional view of the spatial distribution of the Multiscale Model-to-Model (M3C2) distances between the benchmark Terrestrial Laser Scanner (TLS) 3D model and the point cloud produced by Agisoft Photoscan with Low Dynamic Range (LDR) images for the year 2014.
Remotesensing 07 10269 g007

3.3. Comparison between Workflows and Covers

Simple statistical tests and box-whisker plot diagrams were elaborated to allow comparison between the accuracy of the point clouds obtained with different software, procedures and covers (Figure 8 and Figure 9) hence instruments and techniques were the same during the study. As stated earlier, in 2011 the whole glacier was covered by a layer of snow (Figure 5), and therefore, the photographs were quite different from those captured in the years 2012 and 2014. Box-whisker plot diagrams were elaborated using the data from Table 2 and Table 3 and grouping the values according to the year of the field survey (Figure 8A–C) and the cover type of the glacier when the survey was carried out (Figure 8D–F). The RMSE did not show significant differences between the point clouds grouped by years, however, the analysis of the C2C and M3C2 absolute average distances showed that years 2012 and 2014 resulted in more accurate point clouds as compared to 2011 (Figure 8B,C). This result is also supported by the residuals of the camera model parameters that presented the higher values for 2011 (Table 1). During the study, there were not changes in the instruments or the methodological procedures so significant variations in the accuracy of the point clouds are attributed to the changes in the materials covering the glacier. In 2011, the Corral del Veleta was completely covered by a layer of snow while in 2012 and 2014 the debris deposit above the glacier was uncovered. One of the factors determining the accuracy of SfM-MVS methods is the texture of the images used as input. In the case of the year 2011, the photographs presented a poor texture as compared to the debris cover in the photographs of 2012 and 2014. Consequently, more inaccurate point clouds are obtained for snow-covered surfaces (Figure 7E,F) and this fact should be taken into account when analyzing geomorphic changes with multi-temporal approaches. The possibility of getting poor point clouds in areas covered by snow was already hypothesized by recent works [5,31]. Recently, two models of a small glacier partially covered by debris and snow, obtained by means of a TLS and SfM-MVS were compared [25]. This work concluded that the quality of the SfM-MVS model was, in this specific case, mainly determined by the geometry of the images and camera characteristics [25]. However, the former analysis was based on the differences of DEMs interpolated using the point clouds and not directly in the 3D model. An alternative to enhance the performance of SfM-MVS in featureless surfaces based on projecting noise function-based patterns in the data collection phase [45]. This alternative introduces an additional post-processing procedure and should be further explored. On the other hand, the stability of the RMSE over the years and with different covers is due to the fact that the flags used to mark the locations of control points look similar in the photographs independently of the cover over which they were set and the procedure to measure these coordinates over the time was the same. Other recent work [5] reconstructed the relief of a moraine complex in Nepal and found out the presence of artifacts in an area of the scene largely covered by snow. However, in the case of the Corral del Veleta, areas covered by snow did not showed any artifacts when compared to the TLS point cloud and only a reduction in the accuracy of the clouds was showed by the C2C and M3C2 parameters (Figure 8E,F).
According to the RMSEs estimated in the referencing stage and presented in Table 2, Agisoft Photoscan software produced more accurate models than 123D Catch software (Figure 9A). Probably, the bundle adjustment made by Agisoft Photoscan overcomes the procedure developed by 123D Catch software. Additionally, 123D Catch software applies a resolution down-sampling to 3 Mp before processing the images and this effect could be influencing differences observed in Figure 9A and ahead. However, quantifying the down-sampling effect is not possible while 123D Catch is a free available software but the programming code is not available. In the case of the absolute average distances calculated by the C2C and the M3C2 methods Agisoft Photoscan also always got better results, however these differences were slight and not significant from a statistical viewpoint (Figure 9B,C).
In general, unprocessed LDR images got the best RMSE, C2C and M3C2 values. Differences between the point clouds feed with HDR compositions and LDR images were non-significant from a statistical viewpoint, although HDR compositions tended to present a higher variability in RMSE (Figure 9D) and M3C2 distances (Figure 9F). These results agree with the scarce previous experiences [33]. In [33] point clouds of the apse of the Kaisariani Monastery in Greece were produced with Agisoft Photoscan using as input LDR and HDR tone-mapped images. The resulting photo-reconstructions were compared and authors concluded that, from a geometrical viewpoint, the differences between both point clouds were insignificant. However, they just compared the point clouds among them and did not use a benchmark 3D model to estimate the real magnitude of the differences. Previously, [46] explored the use of HDR images in conventional terrestrial photogrammetry concluding that HDR images resulted in orthophotomosaics with geometrical reliability and a higher dynamic range. In [32], authors compared the number of points matched using SfM-MVS techniques and HDR-LDR compositions to produce 3D models of cultural heritage objects. [32] concluded that HDR compositions yielded from 5% to 63% more points matched than LDR images, however differences in the geometrical accuracy of the clouds was not test in this work. In the present work, the amount of points matched within Agisoft Photoscan using HDR pre-processing was slightly higher than the points matched using LDR photographs, producing from 0 to 3% more points matched. In the case of 123D Catch, differences were higher, especially for the year 2011 when 121,758 points matched were obtained using HDR compositions as input as compared to the 89,308 points matched using LDR images. In spite of this increase in the number of points matched, an increase in the geometrical accuracy of the point cloud was not show by the C2C and the M3C2 parameters.
Remotesensing 07 10269 g008 1024
Figure 8. Box plot diagrams elaborated using the datasets showed in Table 2 and Table 3 and grouping these values according to the year of the capture and the cover type. The figure shows the (A) Root Mean Square Error (RMSE) obtained during the referencing procedure and grouped by year, (B) absolute average distance from the point clouds to the benchmark model estimated by the Cloud to Cloud (C2C) method and grouped by year, (C) absolute average distance from the point clouds to the benchmark model estimated by the Multiscale Model to Model (M3C2) method and grouped by year, (D) RMSE obtained during the referencing procedure and grouped by cover type, (E) absolute average distance from the point clouds the benchmark model estimated by the C2C method and grouped by cover type and (F) absolute average distance from the point clouds to the benchmark model estimated by the M3C2 method and grouped by cover type. Note that box plot diagrams show the maximum and the minimum values using the whiskers (upper and lower respectively), the interquartile range (the box) and the median (the line within the box).
Figure 8. Box plot diagrams elaborated using the datasets showed in Table 2 and Table 3 and grouping these values according to the year of the capture and the cover type. The figure shows the (A) Root Mean Square Error (RMSE) obtained during the referencing procedure and grouped by year, (B) absolute average distance from the point clouds to the benchmark model estimated by the Cloud to Cloud (C2C) method and grouped by year, (C) absolute average distance from the point clouds to the benchmark model estimated by the Multiscale Model to Model (M3C2) method and grouped by year, (D) RMSE obtained during the referencing procedure and grouped by cover type, (E) absolute average distance from the point clouds the benchmark model estimated by the C2C method and grouped by cover type and (F) absolute average distance from the point clouds to the benchmark model estimated by the M3C2 method and grouped by cover type. Note that box plot diagrams show the maximum and the minimum values using the whiskers (upper and lower respectively), the interquartile range (the box) and the median (the line within the box).
Remotesensing 07 10269 g008
Remotesensing 07 10269 g009 1024
Figure 9. Box plot diagrams showing the (A) Root Mean Square Errors (RMSE) obtained during the referencing procedure and grouped by the software used for the photo-reconstruction (B) absolute average distance from the point clouds to the benchmark model estimated by the Cloud to Cloud (C2C) method and grouped by the software used for the photo-reconstruction, (C) Absolute average distance from the point clouds to the benchmark model estimated by the Multiscale Model to Model (M3C2) method and grouped by the software used for the photo-reconstruction, (D) RMSE obtained during the referencing procedure and grouped by the type of images used in the photo-reconstruction, (E) absolute average distance from the point clouds to the benchmark model estimated by the C2C method and grouped by the type of images used in the photo-reconstruction, and (F) absolute average distance from the point clouds to the benchmark model estimated by the M3C2 method and grouped by the type of images used in the photo-reconstruction. Note that box plot diagrams show the maximum and the minimum values using the whiskers (upper and lower respectively), the interquartile range (the box) and the median (the line within the box).
Figure 9. Box plot diagrams showing the (A) Root Mean Square Errors (RMSE) obtained during the referencing procedure and grouped by the software used for the photo-reconstruction (B) absolute average distance from the point clouds to the benchmark model estimated by the Cloud to Cloud (C2C) method and grouped by the software used for the photo-reconstruction, (C) Absolute average distance from the point clouds to the benchmark model estimated by the Multiscale Model to Model (M3C2) method and grouped by the software used for the photo-reconstruction, (D) RMSE obtained during the referencing procedure and grouped by the type of images used in the photo-reconstruction, (E) absolute average distance from the point clouds to the benchmark model estimated by the C2C method and grouped by the type of images used in the photo-reconstruction, and (F) absolute average distance from the point clouds to the benchmark model estimated by the M3C2 method and grouped by the type of images used in the photo-reconstruction. Note that box plot diagrams show the maximum and the minimum values using the whiskers (upper and lower respectively), the interquartile range (the box) and the median (the line within the box).
Remotesensing 07 10269 g009
Remotesensing 07 10269 g010 1024
Figure 10. Volumetric point density for the point clouds of the year 2014 and obtained with (A) Agisoft Photoscan using Low Dynamic Range (LDR) images, (B) 123D Catch using LDR images, (C) Agisoft Photoscan using High Dynamic Range (HDR) compositions, (D) 123D Catch using HDR compositions and (E) the Terrestrial Laser Scanner.
Figure 10. Volumetric point density for the point clouds of the year 2014 and obtained with (A) Agisoft Photoscan using Low Dynamic Range (LDR) images, (B) 123D Catch using LDR images, (C) Agisoft Photoscan using High Dynamic Range (HDR) compositions, (D) 123D Catch using HDR compositions and (E) the Terrestrial Laser Scanner.
Remotesensing 07 10269 g010
Due to the nature of 3D point clouds obtained by SfM-MVS techniques, their accuracy is commonly linked to point density. So far, most of the approaches in the literature to estimate point density were carried out gridding the space in two dimensions, projecting the location of points over this surface and accounting the number of points in each cell divided by the cell area. These kinds of approaches could experience unreal estimations in complex and rough reliefs like rock glaciers, riverbanks, gullies, etc. Here, we estimated the volumetric point density, i.e., from each 3D location, a sphere with a volume of 1 m3 (i.e., with a radius of 0.62 m) is defined and the number of points within this volume is accounted. Figure 10 shows the spatial distribution of point densities for each cloud in 2014. Important differences were observed in the median point density for the clouds generated within 123D Catch. With this software, photo-reconstructions elaborated using LDR images presented point densities an order of magnitude higher than those generated using HDR images, with median values of 20 points·m−3 and 0.89 points·m−3, respectively. These results indicate that HDR compositions are not the best input for producing 3D models using 123D Catch software. The exact routine of the matching algorithm used by 123D Catch software is unknown but its performance is clearly affected by the modifications introduced in the HDR compositions, resulting in a lower point density. At the same time, point clouds generated by 123D Catch software presented lower volumetric point densities than point clouds generated by Agisoft Photoscan: 1597 points·m−3 and 1601 points·m−3 using LDR and HDR compositions respectively. This lower point density is probably related to the down-sampling to 3 Mp applied by 123D Catch software before matching the images. Volumetric point densities estimated for the point cloud obtained by means of the TLS device presented the highest value with a median of 12,025 points·m−3.
Finally, an estimation of geomorphic change in the glacier during the study period was not possible because accuracies estimated by the RMSE, the C2C and the M3C2 distances were higher than annual creep velocities and surface lowering of the glacier observed previously [47].

4. Conclusions

In this study, different workflows were tested in order to produce 3D models of the Corral del Veleta rock glacier for three different years and using SfM-MVS techniques. Two different kinds of images were used as input: conventional Low Dynamic Range photographs (LDR) and pre-processed High Dynamic Range (HDR) compositions. At the same time, two software packages (123D Catch and Agisoft Photoscan) were tested and fed with the LDR images and the HDR compositions.
The RMSEs calculated during the referencing and scaling procedures resulted in a global estimated accuracy that ranged from 0.036 to 2.469 m and the M3C2 mean error ranged from 0.084 (standard deviation of 0.403 m) to 1.451 m (standard deviation of 1.625 m). Values of the RMSE presented here contribute to increase the current knowledge about the performance of SfM-MVS techniques over a wide range of scales and landforms and agree (in magnitude) with other previously presented in the literature. Other two parameters, estimated over the whole point cloud were used to analyze the accuracy of the different SfM-MVS pipelines: the Cloud-to-Cloud method (C2C) and the Multiscale Model-to-Model comparison (M3C2). These methods have been proposed recently as the more suitable approaches to estimate the accuracy of 3D models and point clouds. The M3C2 and the C2C parameters presented a similar performance for the 12 analyzed point clouds. However, important differences were observed when comparing the behavior of the M3C2-C2C and the RMSE, suggesting that the later does not reflect totally the accuracy of the point cloud. Consequently, authors suggest the simultaneous use of the RMSE and the M3C2/C2C for future applications. The values of the RMSE, the M3C2 and the C2C showed that the current methodology could be only applied to estimate relatively large changes in the case of the Corral del Veleta rock glacier (>0.30 m) at medium-term time-scale (5 to 10 years).
Probably, the final accuracy obtained here could be improved using a denser network of oblique camera locations, which in this study are highly constrained by the relief to a few sites. It can be interesting to provide estimations on the accuracy of the models obtained with topographic constraints, as this is the usual situation in high mountain areas. The comparison of the standard parameter survey range (also known as relative precision ratio) showed that the accuracy obtained in this work could be notably improved with a convergent and denser camera network geometry, from 1:370 to approximately 1:639, which is the average value for geomorphological features showed by the literature. The spatial distribution of M3C2 and C2C distances did not show any systematic dome-type error due to the geometry of the pose in the study area.
Having into account the different pipelines, the best performance was produced by Agisoft Photoscan software and LDR images. In fact, no significant improvement was experienced using HDR compositions as input in SfM-MVS methods. At the same time, Agisoft Photoscan overcome 123D Catch, producing more accurate and denser point clouds in 11 out 12 cases.
Regarding the relationship between the cover type and the accuracy, the C2C and the M3C2 parameters showed that years without snow cover (2012 and 2014) resulted in more accurate point clouds as compared to 2011, when the rock debris was covered by snow. However, this difference was not appreciated analyzing the values of the RMSE. It seems logical because the RMSE was estimated for artificial points introduced in the scene. Therefore, those researchers who wish to estimate thresholds of geomorphic change based on the accuracy of the 3D model should have into account that the use of the RMSE may be an erroneous strategy.
Findings presented in this work may be of interest for researchers who want to estimate geomorphic changes using SfM-MVS.

Acknowledgments

Authors would like to acknowledge the work, suggestions, comments and revisions made by three anonymous reviewers and the editor of the paper. They provided valuable comments and constructive reviews.

Author Contributions

Álvaro Gómez Gutiérrez implemented the research design, performed data analysis and executed the manuscript writing together with Javier Lozano Parra. José Juan de San José Blasco carried out field work and provided support for referencing and scaling the models. Javier de Matías carried out the capture of the photographs while Fernando Berenguer Sempere carried out the capture, processing and analysis of TLS data.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Gómez-Gutiérrez, Á.; Schnabel, S.; Berenguer-Sempere, F.; Lavado-Contador, F.; Rubio-Delgado, J. Using 3D photo-reconstruction methods to estimate gully headcut erosion. Catena 2014, 120, 91–101. [Google Scholar] [CrossRef]
  2. Debevec, P.E.; Malik, J. Recovering high dynamic range radiance maps from photographs. In Proceedings of the Special Interest Group on Graphics and Interactive Techniques 2008 classes, Los Angeles, CA, USA, 11–15 August 2008; pp. 1–10.
  3. James, M.R.; Robson, S. Straightforward reconstruction of 3D surfaces and topography with a camera: Accuracy and geoscience application. J. Geophys. Res. 2012, 117, 1–17. [Google Scholar] [CrossRef]
  4. Castillo, C.; Pérez, R.; James, M.R.; Quinton, N.J.; Taguas, E.V.; Gómez, A. Comparing the accuracy of several field methods for measuring gully erosion. Soil Sci. Soc. Am. J. 2012, 76, 1319–1332. [Google Scholar] [CrossRef] [Green Version]
  5. Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. “Structure-from-motion” photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef] [Green Version]
  6. Frankl, A.; Stal, C.; Abraha, A.; Nyssen, J.; Rieke-Zapp, D.; De Wulf, A.; Poesen, J. Detailed recording of gully morphology in 3D through image-based modelling. Catena 2015, 127, 92–101. [Google Scholar] [CrossRef] [Green Version]
  7. Lucieer, A.; de Jong, S.; Turner, D. Mapping landslide displacements using structure from motion (SfM) and image correlation of multi-temporal UAV photography. Progr. Phys. Geogr. 2014, 38, 97–116. [Google Scholar] [CrossRef]
  8. Stumpf, A.; Malet, J.P.; Allemand, P.; Pierrot-Deseilligny, M.; Skupinski, G. Ground-based multi-view photogrammetry for the monitoring of landslide deformation and erosion. Geomorphology 2015, 231, 130–145. [Google Scholar] [CrossRef]
  9. Javernick, L.; Brasington, J.; Caruso, B. Modeling the topography of shallow braided rivers using structure-from-motion photogrammetry. Geomorphology 2014, 213, 166–182. [Google Scholar] [CrossRef]
  10. Gómez-Gutiérrez, Á.; de Sanjosé-Blasco, J.; de Matías-Bejarano, J.; Berenguer-Sempere, F. Comparing two photo-reconstruction methods to produce high density point clouds and dems in the corral del veleta rock glacier (Sierra Nevada, Spain). Remote Sens. 2014, 6, 5407–5427. [Google Scholar] [CrossRef]
  11. Ullman, S. The interpretation of structure from motion. Proc. R. Soc. B 1979, 203, 405–426. [Google Scholar] [CrossRef]
  12. Rosnell, T.; Honkavaara, E. Point cloud generation from aerial image data acquired by a quadrocopter type micro unmanned aerial vehicle and a digital still camera. Sensors 2012, 12, 453–480. [Google Scholar] [CrossRef] [PubMed]
  13. Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A comparison and evaluation of multi-view stereo reconstruction algorithms. In Proceeding of the IEEE Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; pp. 519–528.
  14. Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the rangitikei canyon (NZ). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
  15. Agisoft-Photoscan. Available online: http://www.agisoft.com/ (accessed on 24 January 2014).
  16. ARC 3D Webservice. Available online: http://homes.esat.kuleuven.be/~visit3d/webservice/v2/index.php (accessed on 24 January 2014).
  17. Bundler. Available online: http://www.cs.cornell.edu/~snavely/bundler/ (accessed on 24 January 2014).
  18. CMP SfM. Available online: http://ptak.felk.cvut.cz/sfmservice/ (accessed on 24 January 2014).
  19. Micmac. Available online: http://logiciels.ign.fr/?-Micmac,3- (accessed on 15 may 2015).
  20. Photomodeler. Available online: http://www.photomodeler.com/index.html (accessed on 11 June 2015).
  21. VisualSFM. Available online: http://ccwu.me/vsfm/ (accessed on 24 January 2014).
  22. 123D Catch. Available online: http://www.123dapp.com/catch (accessed on 24 January 2014).
  23. Micheletti, N.; Chandler, J.H.; Lane, S.N. Investigating the geomorphological potential of freely available and accessible structure-from-motion photogrammetry using a smartphone. Earth Surf. Process. Landf. 2015, 40, 473–486. [Google Scholar] [CrossRef] [Green Version]
  24. James, M.R.; Ilic, S.; Ruzie, I. Measuring 3D coastal change with a digital camera. In Proceedings of the 7th International Conference on Coastal Dynamics, Bordeaux, France, 24–28 June 2013; pp. 893–904.
  25. Piermattei, L.; Carturan, L.; Guarnieri, A. Use of terrestrial photogrammetry based on structure from motion for mass balance estimation of a small glacier in the Italian Alps. Earth Surf. Process. Landf. 2015, in press. [Google Scholar] [CrossRef]
  26. Turner, D.; Lucieer, A.; de Jong, S. Time series analysis of landslide dynamics using an unmanned aerial vehicle (UAV). Remote Sens. 2015, 7, 1736–1757. [Google Scholar] [CrossRef]
  27. Smith, M.W.; Vericat, D. From experimental plots to experimental landscapes: Topography, erosion and deposition in sub-humid badlands from structure-from-motion photogrammetry. Earth Surf. Process. Landf. 2015, in press. [Google Scholar] [CrossRef]
  28. Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
  29. Koutsoudis, A.; Vidmar, B.; Arnaoutoglou, F. Performance evaluation of a multi-image 3D reconstruction software on a low-feature artefact. J. Archaeol. Sci. 2013, 40, 4450–4456. [Google Scholar] [CrossRef]
  30. Tonkin, T.N.; Midgley, N.G.; Graham, D.J.; Labadz, J.C. The potential of small unmanned aircraft systems and structure-from-motion for topographic surveys: A test of emerging integrated approaches at Cwm Idwal, North Wales. Geomorphology 2014, 226, 35–43. [Google Scholar] [CrossRef] [Green Version]
  31. Fonstad, M.A.; Dietrich, J.T.; Courville, B.C.; Jensen, J.L.; Carbonneau, P.E. Topographic structure from motion: A new development in photogrammetric measurement. Earth Surf. Process. Landf. 2013, 38, 421–430. [Google Scholar] [CrossRef]
  32. Guidi, G.; Gonizzi, S.; Micoli, L.L. Image pre-processing for optimizing automated photogrammetry performances. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, II-5, 145–152. [Google Scholar] [CrossRef]
  33. Kontogianni, G.; Georgopoulos, A. Investigating the effect of hdr images for the 3D documentation of cultural heritage. In Proceedings of the 5th International Conference on Cultural Heritage, Lemessos, Cyprus, 3–8 November 2014; pp. 28–36.
  34. Cai, H. High dynamic range photogrammetry for synchronous luminance and geometry measurement. Lighting Res. Technol. 2013, 45, 230–257. [Google Scholar] [CrossRef]
  35. Cai, H.; Linjie, L. Measuring light and geometry data of roadway environments with a camera. J. Transp. Technol. 2014, 4, 44–62. [Google Scholar] [CrossRef]
  36. Gómez-Ortiz, A.; Oliva, M.; Salvador-Franch, F.; Salvà-Catarineu, M.; Palacios, D.; de Sanjosé-Blasco, J.J.; Tanarro-García, L.M.; Galindo-Zaldívar, J.; de Galdeano, C.S. Degradation of buried ice and permafrost in the Veleta Cirque (Sierra Nevada, Spain) from 2006 to 2013 as a response to recent climate trends. Solid Earth 2014, 5, 979–993. [Google Scholar] [CrossRef]
  37. Gómez-Ortiz, A.; Palacios, D.; Palade, B.; Vázquez-Selem, L.; Salvador-Franch, F. The deglaciation of the Sierra Nevada (Southern Spain). Geomorphology 2012, 159, 93–105. [Google Scholar] [CrossRef]
  38. De Matías-Bejarano, J.; De Sanjosé, J.J.; López-Nicolás, G.; Sagües, C.; Guerrero, J. Photogrammetric methodology for the production of geomorphologic maps: Application to the veleta rock glacier (Sierra Nevada, Granada, Spain). Remote Sens. 2009, 1, 829–841. [Google Scholar] [CrossRef]
  39. Fusion-HDR. Available online: http://fusion-hdr.com/ ( accessed on 26 september 2014).
  40. CloudCompare. Available online: http://www.danielgm.net/cc/ (accessed on 24 January 2014).
  41. Girardeau-Montaut, D.; Roux, M.; Marc, R.; Thibault, G. Change detection on points cloud data acquired with a ground laser scanner. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2005, 36, W19. [Google Scholar]
  42. Wood, J.D.; Fisher, P.F. Assessing interpolation accuracy in elevation models. IEEE Comput. Graph. Appl. 1993, 13, 48–56. [Google Scholar] [CrossRef]
  43. Wheaton, J.M.; Brasington, J.; Darby, S.E.; Sear, D.A. Accounting for uncertainty in dems from repeat topographic surveys: Improved sediment budgets. Earth Surf. Process. Landf. 2010, 35, 136–156. [Google Scholar] [CrossRef]
  44. James, M.R.; Robson, S. Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surf. Process. Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
  45. Koutsoudis, A.; Ioannakis, G.; Vidmar, B.; Arnaoutoglou, F.; Chamzas, C. Using noise function-based patterns to enhance photogrammetric 3D reconstruction performance of featureless surfaces. J. Cult. Herit 2015, in press. [Google Scholar] [CrossRef]
  46. Ntregka, A.; Georgopoulos, A.; Santana Quintero, M. Photogrammetric exploitation of hdr images for cultural heritage documentation. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, II-5/W1, 209–214. [Google Scholar] [CrossRef]
  47. de Sanjosé-Blasco, J.J.; Atkinson-Gordo, A.D.J.; Salvador-Franch, F.; Gómez-Ortiz, A. Application of geomatic techniques to monitoring of the dynamics and to mapping of the Veleta rock glacier (Sierra Nevada, Spain). Zeitschrift fur Geomorphologie Suppl. Issues 2007, 51, 79–89. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Gómez-Gutiérrez, Á.; De Sanjosé-Blasco, J.J.; Lozano-Parra, J.; Berenguer-Sempere, F.; De Matías-Bejarano, J. Does HDR Pre-Processing Improve the Accuracy of 3D Models Obtained by Means of two Conventional SfM-MVS Software Packages? The Case of the Corral del Veleta Rock Glacier. Remote Sens. 2015, 7, 10269-10294. https://doi.org/10.3390/rs70810269

AMA Style

Gómez-Gutiérrez Á, De Sanjosé-Blasco JJ, Lozano-Parra J, Berenguer-Sempere F, De Matías-Bejarano J. Does HDR Pre-Processing Improve the Accuracy of 3D Models Obtained by Means of two Conventional SfM-MVS Software Packages? The Case of the Corral del Veleta Rock Glacier. Remote Sensing. 2015; 7(8):10269-10294. https://doi.org/10.3390/rs70810269

Chicago/Turabian Style

Gómez-Gutiérrez, Álvaro, José Juan De Sanjosé-Blasco, Javier Lozano-Parra, Fernando Berenguer-Sempere, and Javier De Matías-Bejarano. 2015. "Does HDR Pre-Processing Improve the Accuracy of 3D Models Obtained by Means of two Conventional SfM-MVS Software Packages? The Case of the Corral del Veleta Rock Glacier" Remote Sensing 7, no. 8: 10269-10294. https://doi.org/10.3390/rs70810269

APA Style

Gómez-Gutiérrez, Á., De Sanjosé-Blasco, J. J., Lozano-Parra, J., Berenguer-Sempere, F., & De Matías-Bejarano, J. (2015). Does HDR Pre-Processing Improve the Accuracy of 3D Models Obtained by Means of two Conventional SfM-MVS Software Packages? The Case of the Corral del Veleta Rock Glacier. Remote Sensing, 7(8), 10269-10294. https://doi.org/10.3390/rs70810269

Article Metrics

Back to TopTop