Next Article in Journal
New Spectral Fitting Method for Full-Spectrum Solar-Induced Chlorophyll Fluorescence Retrieval Based on Principal Components Analysis
Previous Article in Journal
Validation of Land Cover Maps in China Using a Sampling-Based Labeling Approach
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 7
Issue 8
10.3390/rs70810607
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Aboveground-Biomass Estimation of a Complex Tropical Forest in India Using Lidar

by
Cédric Véga
1,2,*,†,
Udayalakshmi Vepakomma
3,†,
Jules Morel
2,
Jean-Luc Bader
2,
Gopalakrishnan Rajashekar
4,
Chandra Shekhar Jha
4,
Jérôme Ferêt
2,
Christophe Proisy
5,
Raphaël Pélissier
2,5 and
Vinay Kumar Dadhwal
4
1
Laboratoire de l'Inventaire Forestier, Institut National de l'Information Géographique et Forestière, 54000 Nancy, France
2
Institut Français de Pondichéry, UMIFRE CNRS-MAEE 21, Pondicherry 605001, India
3
FPInnovations, 570 Saint-Jean Boulevard, Pointe-Claire, Montrea, QC H9R 3J9, Canada
4
National Remote Sensing Center, Balanagar, Hyderabad 500037, India
5
IRD, UMR AMAP, F-34000 Montpellier, France
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Remote Sens. 2015, 7(8), 10607-10625; https://doi.org/10.3390/rs70810607
Submission received: 14 April 2015 / Revised: 4 August 2015 / Accepted: 12 August 2015 / Published: 18 August 2015
Browse Figures
Versions Notes

Abstract

:
Light Detection and Ranging (Lidar) is a state of the art technology to assess forest aboveground biomass (AGB). To date, methods developed to relate Lidar metrics with forest parameters were built upon the vertical component of the data. In multi-layered tropical forests, signal penetration might be restricted, limiting the efficiency of these methods. A potential way for improving AGB models in such forests would be to combine traditional approaches by descriptors of the horizontal canopy structure. We assessed the capability and complementarity of three recently proposed methods for assessing AGB at the plot level using point distributional approach (DM), canopy volume profile approach (CVP), 2D canopy grain approach (FOTO), and further evaluated the potential of a topographical complexity index (TCI) to explain part of the variability of AGB with slope. This research has been conducted in a mountainous wet evergreen tropical forest of Western Ghats in India. AGB biomass models were developed using a best subset regression approach, and model performance was assessed through cross-validation. Results demonstrated that the variability in AGB could be efficiently captured when variables describing both the vertical (DM or CVP) and horizontal (FOTO) structure were combined. Integrating FOTO metrics with those of either DM or CVP decreased the root mean squared error of the models by 4.42% and 6.01%, respectively. These results are of high interest for AGB mapping in the tropics and could significantly contribute to the REDD+ program. Model quality could be further enhanced by improving the robustness of field-based biomass models and influence of topography on area-based Lidar descriptors of the forest structure.

Graphical Abstract

1. Introduction

Tropical forests store over 40% of the terrestrial carbon and play a major role in the global carbon cycle. A large part of this carbon is sequestered in aboveground biomass (hereafter referred to as AGB or biomass), contributing towards climate regulation [1,2,3]. Consequences on ecosystem functional characteristics and climate changes have been associated with regional changes in biomass. Biomass determines potential carbon emissions that could be released to the atmosphere due to deforestation. Accurate estimation of AGB, especially of tropical forests, is hence necessary to not only understand their influence on water and energy fluxes but assess impacts of carbon losses due to deforestation and forest degradation on global change and environmental degradation [4,5,6,7].
Traditional techniques based on field measurements, particularly using destructive sampling, are considered most accurate in estimating biomass [5,8]. However, field measurements are restricted in terms of spatial distribution, repetitivity and cost, and are generally upscaled to larger areas using remote sensing data [9]. On the other hand, direct measurement of forest carbon stocks using space-borne sensors is also currently not feasible and researchers combine remote sensing based vegetation maps with carbon density values obtained either from the available global databases or local field-based measurements [10,11]. However, tropical forests present a challenging environment for biomass estimation as biomass levels are high, forest canopy is heterogeneous, often tall and largely closed with multiple layering in these forests. Sensor limitation, including spatial resolution, and vegetation complexity have been mainly attributed to poor performance and saturated biomass estimates in tropical forests with both optical and radar data [12,13,14,15]. Moreover, these limitations prevent from assessing rates of forest degradation which are often characterized by subtle changes in the canopy structure. Improving accuracy of biomass mapping could constrain these uncertainties to some extent. Multi-sensor fusion [16] or very high-resolution imagery (VHRI, i.e., <5 m resolution) has shown a promise in overcoming the limitations of individual sensors [17]. For instance, texture analysis of VHRI (1–2 m resolution) of forest canopies that exploits the contrast between sunlit and shadowed part of tree crowns, not only improved details of the outer canopy structure but correlated well with crown size and stand density [18,19]. High potential for biomass mapping was also seen with methods like Fourier Textural Ordination (referred as FOTO [20]) or Gaussian variogram model [21] applied on IKONOS imagery as such textural Indices did not saturate in high biomass ranges of unstratified forest [20,21,22]. Although important, such image-based techniques describe only the horizontal distribution of biomass, thus lacking any insight into vertical description of the canopy structure, a complex issue in multi-layered forests.
The emergence of Light Detection and Ranging (Lidar) in the late 1990s provided new insights in quantifying vegetation distribution in both vertical and horizontal directions and estimating several biophysical parameters from a very fine (tree) to coarser (landscape) scales [23,24]. Owing to the capability of Lidar returns to sample the ground elevation (about 10%–20% penetration to the ground depending on the density of the canopy), accurate measurements of the foliage height and its distribution has been possible [25] using both full waveform as well as discrete return recording sensors [23], even within tropical forests [26]. Studies in different forest ecosystems have shown that both point distributional metrics (DM) and canopy profiles extracted from waveform or discrete return systems are analogous in accurately describing the distribution of biomass in 3D [24,25,27]. From full-waveform data analysis in a tropical context, the height of median energy returns of the canopy profile was reported to be more powerful than total height because it is sensitive to both vertical arrangement and density of canopy elements [28]. Similarly, from using discrete Lidar data, the mean canopy height profile, defined as the vertical center of canopy volume profile, was found to be a good estimator of biomass of tropical forests [29]. Extending the concept of vegetation profile, [24] proposed a voxel-based approach to assess the spatial organization of vegetation material in 3D. Indicators extracted from the so-called Canopy Volume Profile approach (CVP) were found to be more closely related to several of the conventional forest parameters. Similar voxel-based approaches were also successfully used to retrieve forest parameters at stand, plot and tree levels using total frequency of discrete return sampling along height bins of canopy columns [23,30,31,32]. Generally speaking, [33] indicated that structural parameters that combine height and gap fraction, i.e., the fraction of open sky not obstructed by canopy elements [34], improve biomass estimations. Both [35] and [33] also noted that Lidar might not be adapted to quantifying biomass variations in deciduous forests due to saturation effects. The attenuation of the signal is expected to be even more pronounced in multi-layered forest, preventing exhaustive sampling of the whole vegetation stratums. Nevertheless, assuming that crown shape and crown structure is directly related to the vertical foliage profile [36], one might hypothesize that inclusion of crown size and crown density, as achievable from texture analysis of images of the canopy [19], might lead to improved Lidar-based models of biomass, at least at the plot level.
The primary goal of this study is to find a suitable Lidar-based method to estimate aboveground biomass from a local to landscape-scale of tropical wet evergreen forests over a complex terrain. We would like to demonstrate how vertical and horizontal descriptors of the forest canopies could be efficiently combined to develop such a suitable Lidar-based method. Towards this, we will assess the capability and complementarity of recently proposed DM, CVP and FOTO methods applied to Lidar hillshade models of an area with contrasting gradients of stand conditions (post-fire to post-logging and preserved close-canopy), and propose modifications, if necessary, to account for terrain complexity to minimize errors in estimation. This selected 5 km2 Dipterocarp-dominated study site falls within the Western Ghats mountain range and is representative of the landscape. It may be noted that previously developed Lidar-based biomass models for tropical forests [29] were not tested on such high-wood density forests with a highly varying complexity in forest structure or terrain (Figure 1).
Remotesensing 07 10607 g001 1024
Figure 1. Conceptual view of the proposed method for improving biomass models from Lidar data in complex tropical environments.
Figure 1. Conceptual view of the proposed method for improving biomass models from Lidar data in complex tropical environments.
Remotesensing 07 10607 g001

2. Materials

2.1. Study Area

The study site (12°32'47N, 75°40'01E) is located in the Kadamakal Reserve Forest of the Pushpagiri Wildlife Sanctuary in the Southern part of Karnataka, India [37]. Field plots were spread within a 7 km2 area falling inside a watershed whose main river stream is oriented in the Northwest direction (Figure 2). The topography is complex, with altitudes ranging from 90 to 600 m above sea level, and average slope of 24.6° (±14°) but reaching 85° locally. Temperature varies between 25 °C and 30 °C. The rainfall regime showed a strong seasonality due to the Indian southern monsoon [38]. The site receives around 5100 mm of precipitation per year, with 90% received during June–October [39]. The wet evergreen forest characterizing the area belongs to the Dipterocarpus indicus–Kingiodendron pinnatum–Humboldtia brunonis low elevation forest type [40]. Although most of the area experienced selective logging during 1974–1988, previous studies noted that there has been no significant effect on the current stand structure [41]. However, an intense wildfire 25 years ago resulted in patches of semi-evergreen forests with different levels of degradation spread within the area.

2.2. Field Data

Fifteen (N = 15), 1-ha plots (100 m × 100 m) distributed in a gradient of stand structure were established, of which 7 were inventoried in 2009 and 8 in 2010. Each of these 1-ha plots were subdivided into 20 m by 20 m quadrats. Within each quadrat, diameter at breast height (DBH) of all the trees equal or above 10 cm was recorded using a tape (for layout and additional details refer to [22]). Biomass was then estimated at the plot level using a regional allometric model (1) derived by [22] using data acquired by [42]. For these 15 plots, plot biomass ranged from 161 to 687 tons of dry matter per hectare (t∙DM∙ha−1), with an average value of 443 ± 161 t∙DM∙ha−1.
log ( A G B ) = 1.988422 × log ( D B H )
The structural complexity of the plots illustrating the relationship between the plot DBH distribution and the total plot biomass is highlighted in Figure 3.

2.3. Lidar Data

Lidar data was acquired by the National Remote Sensing Centre (Indian Space Research Organization) (Figure 2), between 14–31 December 2005, using Leica ALS 50 (Leica Geosystems, Germany) mounted on an aircraft flown at 2500 m above ground level. This small footprint system records up to 4 returns per pulse emitted at a frequency of 35 kHz with a 24 Hz scanning rate in the infrared domain (1084 nm). With a 44° field of view, the system produced 1455 m swath on the ground. The survey area was covered in 8 flight lines with a 15%–20% line overlap to avoid slivers or gaps in the data. The overall average first return point density was 0.5 hits∙m−2.
Remotesensing 07 10607 g002 1024
Figure 2. Structure of ground topography and canopy height over the study area. Letters refer to plot names.
Figure 2. Structure of ground topography and canopy height over the study area. Letters refer to plot names.
Remotesensing 07 10607 g002
Points describing the ground topography were extracted in-house using Terrascan software (Terrasolid, Finland). Ground classified points represented only 5% of total number of laser hits. A Triangulated Irregular Network was computed from the resulting ground classified points and further rasterized to a 2-m regular Digital Terrain Model (DTM) in ArcGIS (ESRI, Redlands, CA, USA). The height (H) of the non-ground points was calculated by subtracting the corresponding DTM value at the location from the elevation of the point return.
Remotesensing 07 10607 g003 1024
Figure 3. Relationship between plot biomass (upper part) and underlying tree DBH distribution (lower part, jitter representation) highlighting the complex relationship between function and structure.
Figure 3. Relationship between plot biomass (upper part) and underlying tree DBH distribution (lower part, jitter representation) highlighting the complex relationship between function and structure.
Remotesensing 07 10607 g003

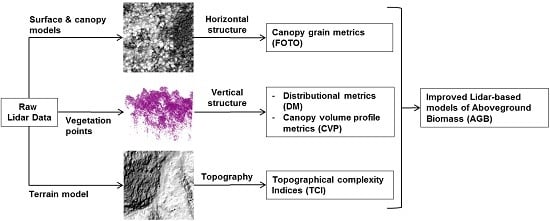
3. Methods

3.1. Registering Field Plots with Lidar

On the field, plot positions were fixed using a Trimble JunoTM SB GPS (Trimble, Sunnyvale, CA, USA) that had a real time positioning accuracy of 2–5 m. Because lower accuracies were expected under forest conditions, plot positioning was further improved by searching for an optimal match between Lidar and plot maximum height in its neighborhood. This was accomplished by moving the plot in incremental steps around a given neighborhood (up to ±50 m in both x and y directions giving a 1 m incremental step in each direction) and computing the elevation difference between field (Hfmax) and Lidar maximum height for every 10 m × 10 m quadrats. Hfmax is the maximum of Hf of each quadrat. Field tree height (Hf) was estimated using DBH to H Equation (2) published by [39] (R2 = 0.67).
log ( H f ) = 0.93 +   0.63 log ( D B H )
The best plot position was fixed at the x, y shifted position where the root mean squared error of height differences is the lowest. Note that since some large tree crowns spread over multiple quadrats, thus affecting Lidar height estimations, 4 plot positions were adjusted visually based on field knowledge and Lidar DTM. Accuracy of positioning of such plots was qualitatively estimated to be beyond 10% of the total plot surface.

3.2. Lidar Parameter Estimation

3.2.1. Distributional Metrics (DM)

First and last Lidar returns vegetation height distributions (i.e., from returns above 2 m in height) were generated for each plot. Based on previous research, 54 metrics were derived from these height distributions [43,44], including:
  • mean height (Mf, Ml for first and last return distribution respectively), height range (Rf, Rl) and coefficient of variation of height (CVf, CVl);
  • quantiles of height computed every 10th percentiles for both first (Pfi, i = 1, 10, …, 100) and last returns (Pli, i = 1, 10, …, 100), complemented by 25th, 75th, 95th and 99th percentiles, i.e., Pf25, Pf75, Pf95, Pf99 for first return distribution and Pl25, Pl75, Pl95, Pl99 for last return distribution;
  • canopy densities, corresponding to proportions of points above given height threshold values. Height thresholds were defined by dividing into 10 equal parts the range between the 95th height percentile and the lowest point height associated with vegetation. The canopy densities of first and last returns, respectively Dfi and Dli (i = 0, 10, …, 90) were then computed as the proportion of points above the corresponding ith threshold value to the total number of points.

3.2.2. Canopy Volume Profile (CVP)

CVP computation was introduced in [24] for fullwaveform data and adapted to discrete Lidar data in [23]. The main steps of the method are summarized below:
  • Each 1-ha plot was divided into volume elements or voxels of 20 m × 20 m × 1 m each. A 20 m horizontal resolution was selected to be in line with the field sampling strategy and ensure at least 1 ground return within each quadrat to ably describe the ground topography.
  • The number of Lidar returns falling in each voxel was counted, and corrected for occlusion effects according to the procedure introduced by [32].
  • Empty voxels were classified into either open (OG) or closed gaps (CG). OG corresponded to those voxels above the first filled voxel with respect to the highest filled voxel within the plot. All the remaining empty voxels were classified as CG.
  • Filled voxels were similarly classified into euphotic (EA) or oligophotic areas (OA). For a given subplot, EA corresponded to the voxels falling within the uppermost 65% of the canopy heights [24]. All the remaining filled voxels were classified as OA.
  • Plot-level statistics were achieved by simply summing the number of voxels belonging to each class.

3.2.3. Canopy Grain Analysis (FOTO)

FOTO is a well-established method to quantify image textural properties [19,20,22]. A brief introduction to the main steps of the method is given below, while more details can be found in [20]. The image data is first divided into continuous unit windows, fixed here to 100 m by 100 m. A 2D Fast Fourier Transform is then applied to each unit window, and the resulting amplitudes are squared to yield a 2-D periodogram providing information about the variability in pixels according to spatial frequencies. Averaging the periodogram across all possible planar directions provided a radial spectrum representing the frequency distribution of the Fourier frequency. The variability of the radial spectra is analyzed by principal component analysis (PCA) and scores of the most prominent axes are used as texture indices [19], which were found to correlate well with various forest biophysical parameters including biomass [22].
FOTO has been efficiently applied to hillshade models generated from Lidar elevation model to analyze the sensitivity of the method to varying sun-view acquisition conditions [45]. In this study, hillshade models of both Lidar digital surface model (DSM) and canopy surface model (CHM, CHM = DSM − DTM) were computed using 4 different azimuths (75°, 165°, 255°, and 345°) using ArcGIS Spatial Analyst. The azimuth line 165°-345° follows the main slope direction of the watershed in which the plots are localized. DSM was generated by selecting the maximum Lidar elevation within a 1 m × 1 m cell and interpolating the empty cells using a natural neighbor method. FOTO metrics were computed at the plot level for each hillshade model. The 3 first PCA axes of either the DSM-based (FD1, FD2, FD3) or CHM-based (FC1, FC2, FC3) hillshade models were then retain for each azimuth.

3.2.4. Terrain Complexity (TC)

Because of the complexity of the ground topography, the plot-level topographic information was reduced through the use of topographical complexity indices (TCI). Such indices aim at summarizing the main terrain features without losing critical topographic information. Here, we followed the method introduced by [46]. First, four terrain attributes were computed from the DTM using a 3 × 3 kernel window (total curvature, terrain rugosity, local relief and local standard deviation). The four terrain attributes were then combined using a normalization factor to deduce the compound terrain complexity index. Finally, plot-level statistics, i.e., mean (TCIM) and standard deviation (TCISD) were computed to evaluate local terrain complexity.

3.3. Model Development and Statistical Analysis

Overall five regression models were developed. The first three aimed at quantifying the potential of DM, CVP and FOTO metrics (benchmark models) to quantify biomass over such complex evergreen tropical humid forest. The last two models aimed at quantifying the potential improvement of biomass estimations resulting from combining 3D-based metrics (i.e., DM or CVP) with both 2D textural indices (i.e., FOTO) and indices of topographical complexity (i.e., TCI).
Predictive linear models were built for each of the five scenarios under study by carrying out a best subset regression analysis. The maximum number of predictors was set to five for parsimony. We only retain models having a variance inflation factor (VIF) below five [47], normally distributed residuals (Shapiro test at a level 0.05) as well as all predictor variables significant at a level 0.01. For each scenario, the overall best model was selected using the corrected Akaike Information Criteria (AICc) [48], which is more adapted to small sample size than AIC [49]. For FOTO, azimuth directions were modelled separately, and only predictor variables computed from the best direction were retained for the two last scenarios. The accuracy of the predictive models was assessed estimating leave-one-out cross-validation (LOOCV) [50], and reporting root mean squared error (RMSEcv) and adjusted determination coefficient (adj. R2). The statistical analyses were performed within R Software, using leaps, car and DAAG packages (cran.r-project.org/).

4. Results

Predictive models resulting from the 5 different sets of Lidar-based parameters are presented in Table 1. The 3 benchmark models (Models 1 to 3) provided cross-validation adj. R2 ranging from 0.74 to 0.90 with corresponding RMSEcv ranging from 17.24% to 10.92%. Among these benchmark models, the best results were obtained using DM (Model 1, ANOVA F-Test, F14,13 = 121, p < 0.001), and included 2 percentiles computed from last returns, representing the highest (Pl99) and lowest (Pl0) values, as well as the median density value computed from the first returns (Df50). The model residuals are unbiased but show an increased variability above 450 t·DM·ha−1 (Figure 4). The model based on CVP (Model 2, ANOVA F-Test, F14,13 = 77.7, p < 0.001) performed almost as good with an RMSEcv of 13.29% and adj. R2 of 0.85 (Table 1). However, the model residuals varied more on the full range of biomass (Figure 4). The poorest model was obtained using FOTO metrics (Model 3, ANOVA F-Test, F14,13 = 41, p < 0.001) computed from hillshade models generated using an azimuth angle of 166°. Model 3 integrated two variables from the CHM (namely, FC1 and FC3) and a variable from the DSM (FD2). It has a 17.24% of RMSEcv and explained 74% of the total variance in biomass. Interestingly, all three of the PCA components were selected in the resulting model. Compared with the two other benchmark models, Model 3 showed a slightly higher residual variability on the full range of biomass (Figure 4). Note that models computed from other azimuth angles were not considered owing to their significantly lower performances (results not reported here).
Table
Table 1. Predictive models of aboveground biomass obtained using the 5 sets of independent variables derived from Lidar data. Model performance includes cross validated root mean squared error (RMSEcv), cross validated adj R2 and corrected Akaike Information Criteria (AICc). FOTO metrics were obtained using an azimuth angle of the light source of 166.
Table 1. Predictive models of aboveground biomass obtained using the 5 sets of independent variables derived from Lidar data. Model performance includes cross validated root mean squared error (RMSEcv), cross validated adj R2 and corrected Akaike Information Criteria (AICc). FOTO metrics were obtained using an azimuth angle of the light source of 166.
ModelMethodEquation RMSEcv t∙DM∙ha−1 (%)Adj. R2AICc
1DMAGB ~ Pl0 + Pl99 + Df5048.42 (10.92)0.90165
2CVPAGB ~ EA + OA + CG **58.94 (13.29)0.85169
3FOTOAGB ~ FC1 + FC3 * + FD276.42 (17.24)0.74181
4DM + FOTO + TCIAGB ~ CVl + Df40 + TCIM + FD328.83 (6.50)0.96156
5CVP + FOTO + TCIAGB ~ EA + OG ** + TCISD + FC3+ FD132.28 (7.28)0.95161
Predictor’s significance levels: 0 “”; 0.001 “*”; 0.01 “**”.
Remotesensing 07 10607 g004 1024
Figure 4. Goodness of fit and residuals of the benchmark models
Figure 4. Goodness of fit and residuals of the benchmark models
Remotesensing 07 10607 g004
Remotesensing 07 10607 g005 1024
Figure 5. Goodness of fit and residuals of the combined models
Figure 5. Goodness of fit and residuals of the combined models
Remotesensing 07 10607 g005
The combination of either DM or CVP with FOTO and TCI (Models 4 and 5) improved model performance. Model 4 (ANOVA F-Test, F14,13 = 366, p < 0.001), including DM, FOTO and TCI explained 96% of the variance in biomass, with an RMSEcv of 6.5%. This model integrated the coefficient of variation of last returns (CVl), a density metrics from first returns (Df40) as well as the average terrain slope complexity (TCIM) and the third component of texture-based PCA from the DSM (FD3). In terms of residuals, the model performed quite well up to 400 t∙DM∙ha−1, and showed a slight increase in variability towards the higher biomass levels (Figure 5). The model that included CVP, FOTO and TCI (Model 5, ANOVA F-Test, F14,13 = 289, p < 0.001) performed only slightly poorer than Model 4, with an adj R2 of 0.95, and an RMSEcv of 7.05%. The model is not biased and showed a homogeneous distribution of the residuals on the full range of biomass (Figure 5). Model 5 included 2 CVP variables, euphotic area (EA) and open gaps (OG), the standard deviation of the terrain complexity index (TCISD), as well as two textural indices from the CHM (FC3) and the DSM (FD1).

4.1. Model Performance

In this gradient of forest structure that varies from burnt to logged and closed-canopy preserved forests, benchmark biomass models (Models 1 to 3) have performed well, showing cross-validated adj R2 values above 0.70 and an RMSEcv in the range 17.24%–10.92%. Among these models, the DM approach (Model 1, Table 1) performed better than others. The model included the two extreme percentiles (i.e., the 99th and 0th) of the last return distribution, giving information on the range of the distribution, as well as the median density of the first returns, providing insights about canopy cover. Such a variable association was expected, their complementarity to assess forest structure having been reported in numerous previous studies [43,44,51]. The model is based on CVP variables (Model 2, Table 1) performed slightly poorer than that of the DM-based one. This result is more surprising because CVP was found to be well correlated with the spatial arrangement of elements within the canopy and the field inventory data [23]. Such a result might be partly explained by the low point density, and the low ground penetration, which prevented the use of a finer voxel resolution. As a consequence, the description of canopy structure might be suboptimal, as noted by the poorer model performance obtained here. The benchmark model developed from FOTO variables (Model 3, Table 1) also suffers from similar limitation. Moreover, hillshade models were generated assuming a Lambertian surface reflectance. Such an opaque surface represents a simplified representation of the canopy properties [45]. These two issues might decrease the quality of the information conveyed by texture and explained the lower performance of the FOTO-based model compared to the one obtained using IKONOS imagery over the same area [22]. Despite this drawback, hillshade models allow a good flexibility for textural analysis. Our results showed that azimuth taken along the slope direction (165° here) provided the best results. Surprisingly CHM-based metrics also performed better using the same azimuthal direction, highlighting the effect of topographical conditions on both forest structure and tree crown architecture. This might be explained by optimization of the shadow patterns along the slope axis, which might also have an incidence on inner tree crown description, and constitute the best acquisition conditions for textural analysis [52]. In addition, we perceive that, while DM metrics were found to be stable with a change in Lidar density [53], both CVP and FOTO approaches may perform better with increased point densities.
Combining either DM or CVP with both FOTO and TCI, the models not only had a direct impact on model performance but also improved description of the plot structure. Models 4 and 5 showed adj. R2 values above 0.95 and corresponding RMSEcv of 6.50% and 7.28% respectively. Model 4 still integrated a density variable providing information on the canopy cover (i.e., Df40). However, height related variables are replaced by the coefficient of variation in height, which summarizes the dispersion of the canopy heights, completed by the third PCA (Fc3) axis computed from the DSM-based hillshade model, and the mean of the TCI (TCIM). In a similar way, CVP-based variables differed slightly between Model 2 and 5. Model 2 included the three variables describing the canopy structure, i.e., euphotic (EA), oligophotic (OA) areas as well as the closed gaps (CG). In Model 5, EA is maintained along with open gaps (OG), which described the variability of the outer canopy, a topographical index (TCISD) and two FOTO metrics: the first and third PCA axes from the CHM and DSM, respectively. Overall, the selection of more general variables from DM and CVP in Models 4 and 5, respectively, suggested that part of the information needed to assess plot biomass is provided by the variables newly integrated. Indeed, [23] showed that the amount of OG characterized well the structure of the canopy surface, and [45] reported that the first PCA axis was well correlated with apparent tree crown size. [39] demonstrated that crown allometries are less affected than stem allometries to site factors, making the former more suitable for predicting forest parameters. In terms of texture, the selection of the third PCA axis (FC3 or FD3) is somehow contradictory with previous studies where it was noted that most of the textural information is synthetized along the two first PCA axes [54]. However, additional research is needed to fully understand the link between FOTO metrics and forest parameters in a range of forest conditions. Apart from texture, a significant difference between Models 4 and 5 is the integration of a topographical variable within Model 5. Such a result was expected because of the demonstrated relationship between forest structure and slope [55], as well as the impact of topography on remote sensing data products. In terms of texture, [22] reported topography induced texture variations in optical images is independent of variations in canopy properties. Similarly, Lidar variables were also found to be sensitive to terrain slope [56]. Indeed, Lidar heights might be inaccurate in slope areas, because individual point height is computed from the DTM independently from the tree structure. As a consequence, point heights are underestimated in part of the crown spreading upslope, and overestimated point height in downslope parts of the crowns [56]. Nevertheless, the fact that topographical variables were only included in one out the five models demonstrated that most of the models compensated for the topographic variability, thus minimizing its effect on model performance.
Despite the fact that DM-based model performed little better than CVP-based one and that Model 5 could not compensate for topographical variability, we would intuitively recommend using CVP-based approaches for estimating biomass, particularly in tropical forests. DM variables were found to be affected by the local forest structure, impeding the development of general models for predicting forest parameters like AGB [57]. Despite lower RMSEcv and AICc values, compared to CVP-based ones, a potential advantage of CVP approach lies in its capacity to provide insights on both the volumetric organization of the canopy in terms of presence (i.e., filled volume) or absence (i.e., gaps) of canopy elements, as well as function of the canopy through the estimation of the euphotic zones characterizing the photosynthetically active area [24]. That said, although CVP-based models performed fairly well across the range of canopy structure and AGB levels considered in this study, we perceive that resolution of the voxels and point density may have a significant impact on biomass estimation. In dense tropical forests, higher point density will be required not only to better describe the 3D arrangement of vegetation structures but also to provide more accurate textural variables and more precise description of ground topography.

4.2. Limitations and Future Work

This study demonstrates for the first time how vertical and horizontal descriptors of the canopy complement each other to improve the performance of Lidar-based models of AGB in multi-layered tropical forests. With RMSE errors below 10%, these results open up new research avenues to map AGB over large areas with a good accuracy. Despite this promising result, uncertainties remain with respect to field-based AGB estimation, plot positioning accuracy and robustness of Lidar descriptors. Here, field biomass was computed using DBH alone due to data limitations. Nevertheless, upon availability, models integrating DBH along with wood specific gravity, total height, and forest type, would provide more accurate estimations [58].
Plot positioning had been a known difficulty with Lidar-based models of forest parameters [59]. The semi-automated method implemented here to overcome the absence of precise GPS measurement performed reasonably well but could not achieve the accuracy that high end tachometers or differential GPS could bring needed for precision forestry. However, positioning errors have a marginal impact on model performance as the large plot sizes (i.e., 1 ha) used here maximizes the overlap between field and Lidar data [60,61].
Future work in Lidar will focus on understanding signal attenuation in different canopy layers, impact of topography on height estimation and derived metrics. While progress has recently been made at tree level [56,62], currently such effects remain difficult to assess on area-based models. This would require simulating forest structure and Lidar signals and developing metrics more robust to the variation in both forest structure and terrain conditions [63].

5. Conclusions

Lidar is a state of the art technology for characterizing forests structures. Currently, most of the Lidar-based models of forest parameters relied on variables describing the vertical properties of the point data at either plot or stand level, thus neglecting information about the horizontal arrangement of forest canopies, which was largely used in 2D optical remote sensing. In dense and multilayered canopies, like those found in the humid tropical forest, the limited capabilities of Lidar signal to penetrate to the ground could limit the potential of such approaches.
In this study, using a coarse density aerial Lidar over a mountainous wet evergreen tropical forest, we assessed the capability, complementarity and enhancement of three recently proposed methods for assessing aboveground biomass at the plot level. The results demonstrated for the first time how traditional descriptors of the vertical canopy structure, derived from either distributional metrics (DM) or canopy volume profiles (CVP), could be efficiently combined with descriptors of the horizontal arrangement of tree crowns derived from canopy grain analysis (FOTO) applied to Lidar hillshade models to improve Lidar-based models of biomass. Introduction of FOTO metrics further improved model accuracy of both DM and CVP approaches by 4.42% (Adj. R2 = 0.96, RMSE = 6.5%) and 6.01% (Adj. R2 = 0.95, RMSE = 7.28%), respectively. The study indicates that for higher accuracy and low topographic effect, DM-based approach could be well adopted. However, CVP-based approach has an additional advantage of providing insights into volumetric organization of the forest canopy.
With RMSEs of aboveground biomass achievable to below 10% using a low density small footprint discrete Lidar (0.5 pts∙m−2) in complex regions, these results show a significant improvement over traditional approaches in addition to providing enhanced description of the forest canopy structures and related functioning. DM and CVP models describe the vertical arrangement of vegetation components, while FOTO metrics provide complementary information on the variability in apparent tree crown size. This comprehensive assessment of forest canopies open up new research avenues to further map AGB over large areas with a good accuracy and can greatly contribute to the REDD+ program.
While the results remain promising, uncertainties in the estimates could be reduced when reference aboveground biomass data set is better established, something that will be possible in the future with improved field equipment and protocols. In addition, more research is needed to better understand how signal extinction influences the robustness of Lidar metrics in multilayered forests, and how the effect of topography on Lidar height estimates could be corrected in area-based approaches. Ground breaking research in tropical forest ecology will also explore how image texture extracted from airborne or satellite imagery could be fused with Lidar data to provide enhanced assessment of AGB at the landscape level.

Acknowledgments

The research has been supported by IFPCAR (Indo-French Promotion Center for Advanced Research) through the joint project number 4509-1 “Controlling for Uncertainty in Assessment of Forest Aboveground Biomass in the Western Ghats of India” between UMR AMAP, Montpellier and the National Remote Sensing Centre, Hyderabad. The authors also greatly acknowledge the French Institute of Pondicherry (IFP) for its financial support to Udayalakshmi Vepakomma for visiting IFP and for providing field control data from its long term monitoring plot in Uppangala.

Author Contributions

The research idea was conceived and conducted by Cédric Véga and Udayalakshmi Vepakomma. Lidar data acquisition and technical support was provided by the NRSC team, Vinay Kumar Dadhwal, Chandra Shekhar Jha and Gopalakrishnan Rajashekar. Jules Morel, Jean-Luc Bader, and Jérôme Ferêt provided support for data computation and analyses. Christophe Proisy and Raphaël Pélissier provided support for the FOTO method, and the latter also contributed to field inventory along with the IFP team. All the authors interpreted the results and contributed in writing the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Bhat, D.M.; Ravindranath, N.H. Above-ground standing biomass and carbon stock dynamics under a varied degree of anthropogenic pressure in tropical rain forests of Uttara Kannada District, Western Ghats, India. Taiwania 2011, 56, 85–96. [Google Scholar]
  2. Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rodenbeck, C.; Altaf Arain, M.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed]
  3. Dixon, R.K.; Brown, S.; Houghton, R.A.; Solomon, A.M.; Trexler, M.C.; Wisniewski, J. Carbon pools and flux of global forest ecosystems. Science 1994, 263, 185–190. [Google Scholar] [CrossRef] [PubMed]
  4. Van der Werf, G.R.; Morton, D.C.; Defries, R.S.; Giglio, L.; Randerson, J.T.; Collatz, G.J.; Kasibhatla, P.S. Estimates of fire emissions from an active deforestation region in the southern Amazon based on satellite data and biogeochemical modelling. Biogeosciences 2009, 6, 235–249. [Google Scholar] [CrossRef]
  5. UNFCC. Kyoto Protocol Reference Manual on Accounting of Emissions Assigned Amount. 2008. Available online: http://unfccc.int/ (accessed on 15 March 2015).
  6. Devagiri, G.M.; Money, S.; Singh, S.; Dadhawal, V.K.; Patil, P.; Khaple, A.; Devakumar, A.S.; Hubballi, S. Assessment of above ground biomass and carbon pool in different vegetation types of south western part of Karnataka, India using spectral modeling. Trop. Ecol. 2013, 54, 149–165. [Google Scholar]
  7. Houghton, R.A. Aboveground forest biomass and the global carbon balance. Glob. Change Biol. 2005, 11, 945–958. [Google Scholar] [CrossRef]
  8. Myneni, R.B.; Dong, J.; Tucker, C.J.; Kaufmann, R.K.; Kauppi, P.E.; Liski, J.; Zhou, L.; Alexeyev, V.; Hughes, M.K. A large carbon sink in the woody biomass of northern forests. Proc. Natl. Acad. Sci. USA 2001, 98, 14784–14789. [Google Scholar] [CrossRef] [PubMed]
  9. Couteron, P.; Barbier, N.; Proisy, C.; Pélissier, R.; Vincent, G. Linking remote-sensing information to tropical forest structure: The crucial role of modelling. Earthzine 2012, 4, 8. [Google Scholar]
  10. Gibbs, H.K.; Brown, S.; Niles, J.O.; Foley, J.A. Monitoring and estimating tropical forest carbon stocks: Making REDD a reality. Environ. Res. Lett. 2007, 2, 045023. [Google Scholar] [CrossRef]
  11. Global Observations of Forest and Land Cover Dynamics (GOFC-GOLD). Monitoring forest carbon stocks and fluxes in the Congo Basin. In Proceedings of COMIFAC Regional Workshop, Brazzaville, Congo, 2–4 February 2010.
  12. Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed]
  13. Asner, G.P. Tropical forest carbon assessment: Integrating satellite and airborne mapping approaches. Environ. Res. Lett. 2009, 4, 034009. [Google Scholar] [CrossRef]
  14. Goetz, S.J.; Baccini, A.; Laporte, N.T.; Johns, T.; Walker, W.; Kellndorfer, J.; Houghton, R.A.; Sun, M. Mapping and monitoring carbon stocks with satellite observations: A comparison of methods. Carbon Balanc. Manag. 2009, 4, 2. [Google Scholar] [CrossRef] [PubMed]
  15. Lu, D. The potential and challenge of remote sensing based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
  16. De Sy, V.; Herold, M.; Achard, F.; Asner, G.P.; Held, A.; Kellndorfer, J.; Verbesselt, J. Synergies of multiple remote sensing data sources for REDD+ monitoring. Curr. Opin. Environ. Sustain. 2012, 4, 696–706. [Google Scholar] [CrossRef]
  17. Hurtt, G.; Xiao, X.; Keller, M.; Palace, M.; Asner, G.P.; Braswell, R.; Brondízio, E.S.; Cardoso, M.; Carvalho, C.J.R.; Fearon, M.G.; et al. IKONOS imagery for the large scale biosphere-atmosphere experiment in Amazonia (LBA). Remote Sens. Environ. 2003, 88, 111–127. [Google Scholar] [CrossRef]
  18. Proisy, C.; Barbier, N.; Guéroult, M.; Pélissier, R.; Gastellu-Etchegorry, J.-P.; Grau, E.; Couteron, P. Biomass Prediction in Tropical Forests: The Canopy Grain Approach. Available online: http://www.intechopen.com/books/remote-sensing-of-biomass-principles-and-applications/biomass-prediction-in-tropical-forest-the-canopy-grain-approach (accessed on 13 August 2015).
  19. Couteron, P.; Pélissier, R.; Nicolini, E.A.; Paget, D. Predicting tropical forest stand structure parameters from Fourier transform of very high-resolution remotely sensed canopy images. J. Appl. Ecol. 2005, 42, 1121–1128. [Google Scholar] [CrossRef] [Green Version]
  20. Proisy, C.; Couteron, P.; Fromard, F. Predicting and mapping mangrove biomass from canopy grain analysis using fourier-based textural ordination of IKONOS images. Remote Sens. Environ. 2007, 109, 379–392. [Google Scholar] [CrossRef]
  21. Coulibaly, L.; Migolet, P.; Adegbidi, G.H.; Fournier, R.; Hervet, E. Mapping aboveground forest biomass from IKONOS satellite image and multi-source geospatial data using neural networks and a Kriging interpolation. In Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS’08), Boston, MA, USA, 7 June–11 June 2008; pp. 298–301.
  22. Ploton, P.; Pélissier, R.; Proisy, C.; Flavenot, T.; Barbier, N.; Rai, S.N.; Couteron, P. Assessing aboveground tropical forest biomass using Google Earth canopy images. Ecol. Appl. 2012, 22, 993–1003. [Google Scholar] [CrossRef] [PubMed]
  23. Coops, N.C.; Hilker, T.; Wulder, M.A.; St-Onge, B.; Newnham, G.; Siggins, A.; Trofymow, J.A. Estimating canopy structure of Douglas-fir forest stands from discrete-return Lidar. Trees 2007, 21, 295–310. [Google Scholar] [CrossRef]
  24. Lefsky, M.A.; Harding, D.; Cohen, W.B.; Parker, G.; Shugart, H.H. Surface Lidar remote sensing of basal area and biomass in deciduous forests of eastern Maryland, USA. Remote Sens. Environ. 1999, 67, 83–98. [Google Scholar] [CrossRef]
  25. Magnussen, S.; Boudewyn, P. Derivations of stand heights from airborne laser scanner data with canopy-based quantile estimators. Can. J. For. Res. 1998, 28, 1016–1031. [Google Scholar] [CrossRef]
  26. Clark, M.L.; Roberts, D.A.; Ewel, J.J.; Clark, D.B. Estimation of tropical rain forest aboveground biomass with small-footprint Lidar and hyperspectral sensors. Remote Sens. Environ. 2011, 115, 2931–2942. [Google Scholar] [CrossRef]
  27. Chasmer, L.; Hopkinson, C.; Smith, B.; Treitz, P. Examining the influence of changing laser pulse repetition frequencies on conifer forest canopy returns. Photogramm. Engin. Remote Sens. 2006, 72, 1359–1367. [Google Scholar] [CrossRef]
  28. Drake, J.B.; Dubayah, R.O.; Clark, D.B.; Knox, R.G.; Blair, J.B.; Hofton, M.A.; Prince, S.D. Estimation of tropical forest structural characteristics using large-footprint Lidar. Remote Sens. Environ. 2002, 79, 305–319. [Google Scholar] [CrossRef]
  29. Asner, G.P.; Hughes, R.F.; Mascaro, J.; Uowolo, A.L.; Knapp, D.E.; Jacobson, J.; Clark, J.K. High-resolution carbon mapping on the million-hectare Island of Hawaii. Front. Ecol. Environ. 2011, 9, 434–439. [Google Scholar] [CrossRef]
  30. Vepakomma, U.; St-Onge, B.; Kneeshaw, D. Response of a boreal forest to canopy opening: assessing vertical and lateral tree growth with multi-temporal Lidar data. Ecol. Appl. 2011, 21, 99–121. [Google Scholar] [CrossRef] [PubMed]
  31. Popescu, S.C.; Zhao, K. A voxel-based Lidar method for estimating crown base height for deciduous and pine trees. Remote Sens. Environ. 2008, 112, 767–781. [Google Scholar] [CrossRef]
  32. Riaño, D.; Meier, E.; Allgöwer, B.; Chuvieco, E.; Ustin, S.L. Modeling airborne laser scanning data for the spatial generation of critical forest parameters in fire behavior modeling. Remote Sens. Environ. 2003, 86, 177–186. [Google Scholar] [CrossRef]
  33. Ni-Meister, W.; Lee, S.; Strahler, A.H.; Woodcock, C.E.; Schaaf, C.; Yao, T.; Blair, J.B. Assessing general relationships between aboveground biomass and vegetation structure parameters for improved carbon estimate from Lidar remote sensing. J. Geophys. Res. Biogeo. 2010, 115, G00E11. [Google Scholar] [CrossRef]
  34. Gonsamo, A.; Walter, J.-M.N.; Pellikka, P. Sampling gap fraction and size for estimating leaf area and clumping indices from hemispherical photographs. Can. J. Forest Res. 2010, 40, 1588–1603. [Google Scholar] [CrossRef]
  35. Nelson, R.F.; Hyde, P.; Johnson, P.; Emessiene, B.; Imhoff, M.L.; Campbell, R.; Edwards, W. Investigating RaDAR-LiDAR synergy in a North Carolina pine forest. Remote Sens. Environ. 2007, 110, 98–108. [Google Scholar] [CrossRef]
  36. Lim, K.; Treitz, P.; Baldwin, I.; Morrisson, J.; Green, J. Lidar remote sensing of biophysical properties of northern tolerant hardwood forests. Can. J. Remote Sens. 2003, 29, 658–678. [Google Scholar] [CrossRef]
  37. Pélissier, R.; Pascal, J.-P.; Ayyappan, N.; Ramesh, B.R.; Aravajy, S.; Ramalingam, S.R. Twenty years tree demography in an undisturbed Dipterocarp permanent sample plot at Uppangala, Western Ghats of India—Data Paper. Ecology 2011, 92, 1376. [Google Scholar] [CrossRef]
  38. Pascal, J.-P.; Pélissier, R. Structure and floristic composition of a tropical evergreen forest in South-West India. J. Trop. Ecol. 1996, 12, 191–214. [Google Scholar] [CrossRef]
  39. Antin, C.; Pélissier, R.; Vincent, G.; Couteron, P. Crown allometries are less responsive than stem allometry to tree size and habitat variations in an Indian monsoon forest. Trees 2013, 27, 1485–1495. [Google Scholar] [CrossRef]
  40. Pascal, J.-P. Wet Evergreen Forests of the Western Ghats of India: Ecology, Structure, Floristic Composition and Succession (Travaux de la Section Scientifique et Technique); Institut Français de Pondichéry: Puducherry, India, 1988. [Google Scholar]
  41. Pélissier, R.; Pascal, J.-P.; Houllier, F.; Laborde, H. Impact of selective logging on the dynamics of a low elevation dense moist evergreen forest in the Western Ghats (South India). For. Ecol. Manag. 1998, 105, 107–119. [Google Scholar] [CrossRef]
  42. Rai, S.N. Productivity of Tropical Rain Forests of Karnataka. Ph.D. Thesis, University of Bombay, Bombay, India, 1981. [Google Scholar]
  43. Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
  44. Means, J.E.; Acker, S.A.; Fitt, B.J.; Renslow, M.; Emerson, L.; Hendrix, C.J. Predicting forest stand characteristics with airborne scanning Lidar. Photogramm. Eng. Remote Sens. 2000, 66, 1367–1371. [Google Scholar]
  45. Barbier, N.; Proisy, C.; Véga, C.; Sabatier, D.; Couteron, P. Bidirectional texture function of high resolution optical images of tropical forest: An approach using LiDAR hillshade simulations. Remote Sens. Environ. 2011, 115, 167–179. [Google Scholar] [CrossRef]
  46. Lu, H.; Liu, X.; Bian, L. Terrain complexity: Definition, index, and DEM resolution. Proc. SPIE 2007, 6753, 675323. [Google Scholar]
  47. O’Brien, R.M. A caution regarding rules of thumb for variance inflation factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
  48. Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: New York, NY, USA, 2002; p. 488. [Google Scholar]
  49. Hurvich, C.M.; Tsai, C.-L. Regression and time series model selection in small samples. Biometrika 1989, 76, 297–307. [Google Scholar] [CrossRef]
  50. Picard, R.R.; Cook, R.D. Cross-validation of regression models. J. Am. Stat. Assoc. 1984, 79, 575–583. [Google Scholar] [CrossRef]
  51. Hall, S.A.; Burke, I.C.; Box, D.O.; Kaufmann, M.R.; Stoker, J.M. Estimating stand structure using discrete-return Lidar: An example from low density, fire prone ponderosa pine forests. For. Ecology Manag. 2005, 208, 189–209. [Google Scholar] [CrossRef]
  52. Barbier, N.; Couteron, P. Attenuating the bidirectional texture variation of satellite images of tropical forests: No use to cry for a shadow! Remote Sens. Environ. 2015. submitted. [Google Scholar]
  53. Jakubowski, M.K.; Guo, Q.; Kelly, M. Tradeoffs between Lidar pulse density and forest measurement accuracy. Remote Sens. Environ. 2013, 130, 245–253. [Google Scholar] [CrossRef]
  54. Barbier, N.; Couteron, P.; Proisy, C.; Malhi, Y.; Gastellu-Etchegorry, J.-P. The variation of apparent crown size and canopy heterogeneity across lowland Amazonian forests. Glob. Ecol. Biogeo. 2010, 19, 72–84. [Google Scholar] [CrossRef]
  55. Robert, A.; Moravie, M.-A. Topographic variation and stand structure heterogeneity in a wet evergreen forest of India. J. Trop. Ecol. 2003, 19, 697–707. [Google Scholar] [CrossRef]
  56. Véga, C.; Hamrouni, A.; El Mokhtari, S.; Morel, J.; Bock, J.; Renaud, J.-P.; Bouvier, M.; Durrieu, S.P. Trees: A point-based approach to forest tree extraction from Lidar data. Inter. J. Appl. Earth Observ. Geoinf. 2014, 33, 98–108. [Google Scholar] [CrossRef]
  57. Meyer, V.; Saatchi, S.S.; Chave, J.; Dalling, J.W.; Bohlman, S.; Fricker, G.A.; Hubbell, S. Detecting tropical forest biomass dynamics from repeated airborne Lidar measurements. Biogeosciences 2013, 10, 5421–5438. [Google Scholar] [CrossRef]
  58. Chave, J.; Andalo, C.; Brown, S.; Cairns, M.; Chambers, J.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef] [PubMed]
  59. Gobakken, T.; Næsset, E. Assessing effects of positioning errors and sample plot size on biophysical stand properties derived from airborne laser scanner data. Can. J. For. Res. 2009, 39, 1036–1052. [Google Scholar] [CrossRef]
  60. Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of Lidar-derived estimates of forest stand biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
  61. Ruiz, L.A.; Hermosilla, T.; Mauro, F.; Godino, M. Analysis of the influence of plot size and Lidar density on forest structure attribute estimates. Forests 2014, 5, 936–951. [Google Scholar] [CrossRef]
  62. Khosravipour, A.; Skidmore, A.K.; Wang, T.; Isenburg, M.; Khoshelham, K. Effect of slope on treetop detection using a Lidar canopy height model. ISPRS J. Photogramm. Remote Sens. 2015, 104, 44–52. [Google Scholar] [CrossRef]
  63. Véga, C.; Renaud, J.P.; Durrieu, S.; Bouvier, M. On the interest of penetration depth, canopy area and volume metrics to improve Lidar-based models of forest parameters. Remote Sens. Environ. 2015. submitted. [Google Scholar]

Share and Cite

MDPI and ACS Style

Véga, C.; Vepakomma, U.; Morel, J.; Bader, J.-L.; Rajashekar, G.; Jha, C.S.; Ferêt, J.; Proisy, C.; Pélissier, R.; Dadhwal, V.K. Aboveground-Biomass Estimation of a Complex Tropical Forest in India Using Lidar. Remote Sens. 2015, 7, 10607-10625. https://doi.org/10.3390/rs70810607

AMA Style

Véga C, Vepakomma U, Morel J, Bader J-L, Rajashekar G, Jha CS, Ferêt J, Proisy C, Pélissier R, Dadhwal VK. Aboveground-Biomass Estimation of a Complex Tropical Forest in India Using Lidar. Remote Sensing. 2015; 7(8):10607-10625. https://doi.org/10.3390/rs70810607

Chicago/Turabian Style

Véga, Cédric, Udayalakshmi Vepakomma, Jules Morel, Jean-Luc Bader, Gopalakrishnan Rajashekar, Chandra Shekhar Jha, Jérôme Ferêt, Christophe Proisy, Raphaël Pélissier, and Vinay Kumar Dadhwal. 2015. "Aboveground-Biomass Estimation of a Complex Tropical Forest in India Using Lidar" Remote Sensing 7, no. 8: 10607-10625. https://doi.org/10.3390/rs70810607

APA Style

Véga, C., Vepakomma, U., Morel, J., Bader, J. -L., Rajashekar, G., Jha, C. S., Ferêt, J., Proisy, C., Pélissier, R., & Dadhwal, V. K. (2015). Aboveground-Biomass Estimation of a Complex Tropical Forest in India Using Lidar. Remote Sensing, 7(8), 10607-10625. https://doi.org/10.3390/rs70810607

Article Metrics

Back to TopTop