Reconstruction of Satellite-Retrieved Land-Surface Reflectance Based on Temporally-Continuous Vegetation Indices
Abstract
:1. Introduction
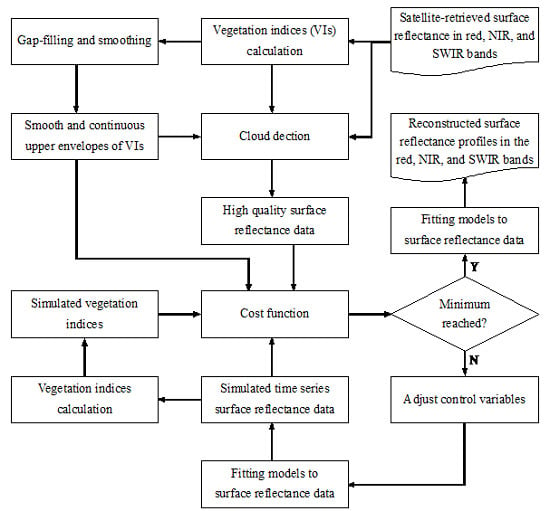
2. Methodology and Data

2.1. Gap filling and Smoothing of Vegetation Indices
2.2. Cloud Detection of Surface Reflectance
2.3. Surface Reflectance Reconstruction
2.4. Data
| No. Bands | Band Name | Band Width (nm) |
|---|---|---|
| B1 | Red | 620–670 |
| B2 | NIR | 841–876 |
| B3 | Blue | 459–479 |
| B4 | Green | 545–565 |
| B5 | NIR | 1230–1250 |
| B6 | SWIR | 1628–1652 |
| B7 | SWIR | 2105–2155 |
| Site Name | Country | Latitude (°) | Longitude (°) | Land Cover Types |
|---|---|---|---|---|
| Alpilles | France | 43.81 | 4.74 | Cropland |
| Yucheng | China | 36.95 | 116.60 | Cropland |
| Konza | USA | 39.08 | −96.62 | Grassland |
| Counami | French Guyana | 5.34 | −53.24 | Evergreen broadleaf forest |
| Tapajos | Brazil | −2.87 | −54.95 | Evergreen broadleaf forest |
3. Result Analysis
3.1. Comparison in Space




3.2. Temporal Analysis





4. Discussions
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liang, S.; Zhang, X.; Xiao, Z.; Liu, Q.; Cheng, J.; Zhao, X. Global LAnd Surface Satellite (GLASS) Products: Algorithms, Validation and Analysis; Springer: New York, NY, USA, 2013; pp. 3–69. [Google Scholar]
- Vermote, E.F.; El Saleous, N.Z.; Justice, C.O. Atmospheric correction of MODIS data in the visible to middle infrared: first results. Remote Sens. Environ. 2002, 83, 97–111. [Google Scholar] [CrossRef]
- Vermote, E.F.; Justice, C.; Csiszar, I. Early evaluation of the VIIRS calibration, cloud mask and surface reflectance Earth data records. Remote Sens. Environ. 2014, 148, 134–145. [Google Scholar] [CrossRef]
- Rossow, W.B.; Garder, L.C. Cloud detection using satellite measurements of infrared and visible radiances for ISCCP. J. Clim. 1993, 6, 2341–2369. [Google Scholar] [CrossRef]
- Ackerman, S.A.; Strabala, K.I.; Menzel, W.P.; Frey, R.A.; Moeller, C.C.; Gumley, L.E. Discriminating clear sky from clouds with MODIS. J. Geophys. Res. 1998, 103, 32141–32157. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y.; Frey, R. An automatic cloud mask algorithm based on time series of MODIS measurements. J. Geophys. Res. 2008, 113, D16207. [Google Scholar] [CrossRef]
- Jonsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
- Chen, J.; Jonsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Liang, S.; Fang, H.; Chen, M. Atmospheric correction of Landsat ETM+ land surface imagery—Part I: methods. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2490–2498. [Google Scholar] [CrossRef]
- Liu, R.; Liu, Y. Generation of new cloud masks from MODIS land surface reflectance products. Remote Sens. Environ. 2013, 133, 21–37. [Google Scholar] [CrossRef]
- Tang, H.; Yu, K.; Hagolle, O.; Jiang, K.; Geng, X.; Zhao, Y. Cloud detection method based on a time series of MODIS surface reflectance images. Int. J. Digit. Earth 2013, 6, 157–171. [Google Scholar] [CrossRef]
- Liang, S.; Zhao, X.; Yuan, W.; Liu, S.; Cheng, X.; Xiao, Z.; Zhang, X.; Liu, Q.; Cheng, J.; Tang, H.; et al. A long-term Global LAnd Surface Satellite (GLASS) dataset for environmental studies. Int. J. Digit. Earth 2013, 6, 5–33. [Google Scholar] [CrossRef]
- Murphy, R.E.; Barnes, W.L.; Lyapustin, A.I.; Privette, J.; Welsch, C.; DeLuccia, F.; Swenson, H.; Schueler, C.F.; Ardanuy, P.E.; Kealy, P.S.M. Using VIIRS to provide data continuity with MODIS. In Proceedings of the 2001 IEEE International Geoscience and Remote Sensing Symposium, Sydney, NSW, Australia, 9–13 July 2001; Volume 3, pp. 1212–1214.
- Lewis, J.M.; Martin, D.W.; Rabin, R.M.; Moosmüller, H. Suomi: Pragmatic visionary. Bull. Amer. Meteor. Soc. 2010, 91, 559–577. [Google Scholar] [CrossRef]
- Vina, A.; Gitelson, A.A.; Nguy-Robertson, A.L.; Peng, Y. Comparison of different vegetation indices for the remote assessment of green leaf area index of crops. Remote Sens. Environ. 2011, 115, 3468–3478. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of leaf-area index from quality of light on forest floor. Ecology 1969, 50, 663. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium, Washington, DC, USA, 10–14 December 1973; Freden, S.C., Mercanti, E.P., Becker, M.A., Eds.; NASA: Washington, DC, USA, 1974. [Google Scholar]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Huete, A.R.; Liu, H.Q.; Batchily, K.; Leeuwen, W. A comparison of vegetation indices global set of TM images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Tucker, C.J.; Sellers, P.J. Satellite remote sensing of primary production. Int. J. Remote Sens. 1986, 7, 1395–1416. [Google Scholar] [CrossRef]
- Viovy, N.; Arino, O.; Belward, A.S. The best index slope extraction (BISE)—A method for reducing noise in NDVI time-series. Int. J. Remote Sens. 1992, 13, 1585–1590. [Google Scholar] [CrossRef]
- Hermance, J.F. Stabilizing high-order, non-classical harmonic analysis of NDVI data for average annual models by damping model roughness. Int. J. Remote Sens. 2007, 28, 2801–2819. [Google Scholar] [CrossRef]
- Roerink, G.J.; Menenti, M.; Verhoef, W. Reconstructing cloud free NDVI composites using Fourier analysis of time series. Int. J. Remote Sens. 2000, 21, 1911–1917. [Google Scholar] [CrossRef]
- Garcia, D. Robust smoothing of gridded data in one and higher dimensions with missing values. Comput. Stat. Data Anal. 2010, 54, 1167–1178. [Google Scholar] [CrossRef] [PubMed]
- Rousseeuw, P.J.; Leroy, A.M. Robust Regression and Outlier Detection; John Wiley & Sons, Inc.: New York, NY, USA, 1987. [Google Scholar]
- Rousseeuw, P.J.; Croux, C. Alternatives to the median absolute deviation. J. Am. Statist. Assoc. 1993, 88, 1273–1283. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, K. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Baret, F.; Morisette, J.T.; Fernandes, R.A.; Champeaux, J.L.; Myneni, R.B.; Chen, J.; Plummer, S.; Weiss, M.; Bacour, C.; Garrigues, S.; et al. Evaluation of the representativeness of networks of sites for the global validation and intercomparison of land biophysical products: Proposition of the CEOS-BELMANIP. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1794–1803. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Z.; Liang, S.; Wang, T.; Liu, Q. Reconstruction of Satellite-Retrieved Land-Surface Reflectance Based on Temporally-Continuous Vegetation Indices. Remote Sens. 2015, 7, 9844-9864. https://doi.org/10.3390/rs70809844
Xiao Z, Liang S, Wang T, Liu Q. Reconstruction of Satellite-Retrieved Land-Surface Reflectance Based on Temporally-Continuous Vegetation Indices. Remote Sensing. 2015; 7(8):9844-9864. https://doi.org/10.3390/rs70809844
Chicago/Turabian StyleXiao, Zhiqiang, Shunlin Liang, Tongtong Wang, and Qiang Liu. 2015. "Reconstruction of Satellite-Retrieved Land-Surface Reflectance Based on Temporally-Continuous Vegetation Indices" Remote Sensing 7, no. 8: 9844-9864. https://doi.org/10.3390/rs70809844
APA StyleXiao, Z., Liang, S., Wang, T., & Liu, Q. (2015). Reconstruction of Satellite-Retrieved Land-Surface Reflectance Based on Temporally-Continuous Vegetation Indices. Remote Sensing, 7(8), 9844-9864. https://doi.org/10.3390/rs70809844