Relative Efficiency of ALS and InSAR for Biomass Estimation in a Tanzanian Rainforest
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Field Data

| Plot Size(m2) | Mean Biomass(Mg∙ha−1) | SD(Mg∙ha−1) |
|---|---|---|
| 700 | 371.8 | 221.5 |
| 900 | 366.1 | 216.3 |
| 1100 | 365.6 | 203.0 |
| 1300 | 361.0 | 190.5 |
| 1500 | 354.2 | 180.4 |
| 1700 | 355.0 | 170.2 |
| 1900 | 351.1 | 159.6 |
2.3. ALS Data
| Parameters | Value |
|---|---|
| Flight speed (m∙s−1) | 70 |
| Flying altitude (m a.g.l.) | 800 |
| Scanner frequency (kHz) | 339 |
| Footprint size (cm) | 22 |
| Beam divergence (mrad) | 0.28 |
| Half scan angle (deg.) | 16 |
2.4. InSAR Data
2.5. ALS-Derived Explanatory Variables
2.6. InSAR-Derived Explanatory Variable
2.7. DTM-Derived Explanatory Variable
2.8. Tessellating the Study Area and the Remotely Sensed Data
2.9. Model Construction
| Model | Model Form a |
|---|---|
| TE | ln(biomass) = ln(terrain elevation) |
| ALS | ln(biomass) = ln(H60.F) + ln(D1.L) |
| InSAR | ln(biomass) = ln(InSAR height) |
2.10. Model-Based Inference
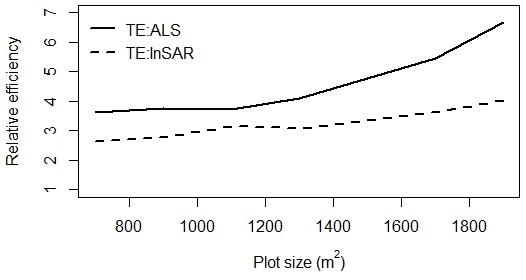
2.11. Relative Efficiency
3. Results and Discussion






| Plot Size | N | TE | ALS | InSAR | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (Mg∙ha−1) | SE (Mg∙ha−1) | SE (%) | (Mg∙ha−1) | SE (Mg∙ha−1) | SE (%) | (Mg∙ha−1) | SE (Mg∙ha−1) | SE (%) | ||
| 700 | 126,772 | 442.2 | 67.6 | 15.3 | 352.9 | 35.5 | 10.1 | 368.0 | 41.7 | 11.3 |
| 900 | 98,635 | 449.1 | 67.6 | 15.0 | 346.1 | 34.9 | 10.1 | 365.7 | 40.5 | 11.1 |
| 1100 | 80,667 | 458.6 | 64.5 | 14.1 | 356.3 | 33.5 | 9.4 | 369.1 | 36.3 | 9.8 |
| 1300 | 68,279 | 443.6 | 57.8 | 13.0 | 350.5 | 28.5 | 8.1 | 361.0 | 32.8 | 9.1 |
| 1500 | 59,154 | 435.7 | 52.1 | 11.9 | 345.5 | 23.8 | 6.9 | 354.2 | 28.4 | 8.0 |
| 1700 | 52,214 | 435.0 | 47.9 | 11.0 | 346.4 | 20.5 | 5.9 | 354.2 | 25.2 | 7.1 |
| 1900 | 46,727 | 427.2 | 45.1 | 10.6 | 341.4 | 17.5 | 5.1 | 350.3 | 22.5 | 6.4 |



4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- UNFCCC. Report of the Conference of the Parties on its Sixteenth Session, held in Cancun from 29 November to 10 December 2010. Addendum. Part two: Action taken by the Conference of the Parties at its Sixteenth Session; United Nations Office: Geneva, Switzerland, 2011; p. 31. [Google Scholar]
- UNFCCC. Report of the Conference of the Parties on its Fifteenth Session, held in Copenhagen from 7 to 19 December 2009. Addendum. Part Two: Action taken by the Conference of the Parties at its Fifteenth Session; United Nations Office: Geneva, Switzerland, 2010; p. 43. [Google Scholar]
- FAO. Forest resources of the world. In Unasylva; 1948; Available online: http://www.fao.org/docrep/x5345e/x5345e00.htm (accessed on 16 January 2015).
- Boyd, D.S.; Danson, F.M. Satellite remote sensing of forest resources: Three decades of research development. Progr. Phys. Geogr. 2005, 29, 1–26. [Google Scholar] [CrossRef]
- Bohlin, J.; Wallerman, J.; Fransson, J.E.S. Forest variable estimation using photogrammetric matching of digital aerial images in combination with a high-resolution DEM. Scand. J. Forest Res. 2012, 27, 692–699. [Google Scholar] [CrossRef]
- Persson, H.; Wallerman, J.; Olsson, H.; Fransson, J.E.S. Estimating forest biomass and height using optical stereo satellite data and a DTM from laser scanning data. Can. J. Remote Sens. 2013, 39, 251–262. [Google Scholar] [CrossRef]
- Gobakken, T.; Bollandsås, O.M.; Næsset, E. Comparing biophysical forest characteristics estimated from photogrammetric matching of aerial images and airborne laser scanning data. Scand. J. Forest Res. 2014, 30, 1–14. [Google Scholar] [CrossRef]
- Næsset, E. Determination of mean tree height of forest stands by digital photogrammetry. Scand. J. Forest Res. 2002, 17, 446–459. [Google Scholar] [CrossRef]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Hansen, E.; Gobakken, T.; Bollandsås, O.; Zahabu, E.; Næsset, E. Modeling aboveground biomass in dense tropical submontane rainforest using airborne laser scanner data. Remote Sens. 2015, 7, 788–807. [Google Scholar] [CrossRef] [Green Version]
- Fassnacht, F.E.; Hartig, F.; Latifi, H.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Gobakken, T.; Næsset, E. Assessing effects of positioning errors and sample plot size on biophysical stand properties derived from airborne laser scanner data. Can. J. For. Res. 2009, 39, 1036–1052. [Google Scholar] [CrossRef]
- Mascaro, J.; Detto, M.; Asner, G.P.; Muller-Landau, H.C. Evaluating uncertainty in mapping forest carbon with airborne LiDAR. Remote Sens. Environ. 2011, 115, 3770–3774. [Google Scholar] [CrossRef]
- Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of LiDAR-derived estimates of forest stand biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Hernández-Stefanoni, J.; Dupuy, J.; Johnson, K.; Birdsey, R.; Tun-Dzul, F.; Peduzzi, A.; Caamal-Sosa, J.; Sánchez-Santos, G.; López-Merlín, D. Improving species diversity and biomass estimates of tropical dry forests using airborne LiDAR. Remote Sens. 2014, 6, 4741–4763. [Google Scholar] [CrossRef]
- Mauya, E.; Hansen, E.H.; Gobakken, T.; Bollandsås, O.M.; Malimbwi, R.E.; Næsset, E. Effects of field plot size on prediction accuracy of aboveground biomass in airborne laser scanning-assisted inventories in tropical rain forests of Tanzania. Carbon Balanc. Manage. 2015. submitted. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Næsset, E. Determination of mean tree height of forest stands using airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1997, 52, 49–56. [Google Scholar] [CrossRef]
- Næsset, E. Estimating timber volume of forest stands using airborne laser scanner data. Remote Sens. Environ. 1997, 61, 246–253. [Google Scholar] [CrossRef]
- Næsset, E.; Bollandsås, O.M.; Gobakken, T. Comparing regression methods in estimation of biophysical properties of forest stands from two different inventories using laser scanner data. Remote Sens. Environ. 2005, 94, 541–553. [Google Scholar] [CrossRef]
- Li, Y.Z.; Andersen, H.E.; McGaughey, R. A comparison of statistical methods for estimating forest biomass from light detection and ranging data. West. J. Appl. For. 2008, 23, 223–231. [Google Scholar]
- Clark, D.B.; Kellner, J.R. Tropical forest biomass estimation and the fallacy of misplaced concreteness. J. Veg. Sci. 2012, 23, 1191–1196. [Google Scholar] [CrossRef]
- Köhl, M.; Magnussen, S.; Marchetti, M. Sampling Methods, Remote Sensing and GIS Multiresource Forest Inventory; Springer: Berlin, Germany, 2006; p. 365. [Google Scholar]
- Gregoire, T.G. Design-based and model-based inference in survey sampling: Appreciating the difference. Can. J. For. Res. 1998, 28, 1429–1447. [Google Scholar] [CrossRef]
- Payandeh, B. Relative efficiency of two-dimensional systematic sampling. For. Sci. 1970, 16, 271–276. [Google Scholar]
- Ene, L.T.; Næsset, E.; Gobakken, T.; Gregoire, T.G.; Stahl, G.; Nelson, R. Assessing the accuracy of regional LiDAR-based biomass estimation using a simulation approach. Remote Sens. Environ. 2012, 123, 579–592. [Google Scholar] [CrossRef]
- Næsset, E. Area-based inventory in Norway—From innovation to an operational reality. In Forestry Applications of Airborne Laser Scanning; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer: Dordrecht, The Netherlands, 2014; Volume 27, pp. 215–240. [Google Scholar]
- Hamilton, A.C.; Bensted-Smith, R. Forest Conservation in the East Usambara Mountains, Tanzania; IUCN-The World Conservation Union; Dar es Salaam, Tanzania: Forest Division, Ministry of Lands, Natural Resources, and Tourism, United Republic of Tanzania: Gland, Switzerland/Cambridge, UK, 1989; p. 392. [Google Scholar]
- Haglöf Sweden. Users Guide Vertex III V1.5 and Transponder T3; Haglöf Sweden AB: Långsele, Sweden, 2007. [Google Scholar]
- Tomppo, E.; Malimbwi, R.; Katila, M.; Mäkisara, K.; Henttonen, H.M.; Chamuya, N.; Zahabu, E.; Otieno, J. A sampling design for a large area forest inventory: Case Tanzania. Can. J. For. Res. 2014, 44, 931–948. [Google Scholar] [CrossRef]
- Masota, A.M.; Zahabu, E.; Malimbwi, R.; Bollandsås, O.M.; Eid, T. Tree allometric models for above- and belowground biomass of tropical rainforests in Tanzania. South. For. J. Forest Sci. 2015. submitted. [Google Scholar]
- Soininen, A. TerraScan User’s Guide; Terrasolid Oy: Jyvaskyla, Finland, 2012. [Google Scholar]
- Axelsson, P. DEM generation from laser scanner data using adaptive TIN models. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2000, 33, 110–117. [Google Scholar]
- Ioki, K.; Tsuyuki, S.; Hirata, Y.; Phua, M.-H.; Wong, W.V.C.; Ling, Z.-Y.; Saito, H.; Takao, G. Estimating above-ground biomass of tropical rainforest of different degradation levels in Northern Borneo using airborne LiDAR. For. Ecol. Manage. 2014, 328, 335–341. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T.; Solberg, S.; Gregoire, T.G.; Nelson, R.; Stahl, G.; Weydahl, D. Model-assisted regional forest biomass estimation using LiDAR and InSAR as auxiliary data: A case study from a boreal forest area. Remote Sens. Environ. 2011, 115, 3599–3614. [Google Scholar] [CrossRef]
- Marshall, A.R.; Willcock, S.; Platts, P.J.; Lovett, J.C.; Balmford, A.; Burgess, N.D.; Latham, J.E.; Munishi, P.K.T.; Salter, R.; Shirima, D.D.; et al. Measuring and modelling above-ground carbon and tree allometry along a tropical elevation gradient. Biol. Conserv. 2012, 154, 20–33. [Google Scholar]
- Means, J.E.; Acker, S.A.; Harding, D.J.; Blair, J.B.; Lefsky, M.A.; Cohen, W.B.; Harmon, M.E.; McKee, W.A. Use of large-footprint scanning airborne lidar to estimate forest stand characteristics in the Western Cascades of Oregon. Remote Sens. Environ. 1999, 67, 298–308. [Google Scholar] [CrossRef]
- Lim, K.; Treitz, P.; Baldwin, K.; Morrison, I.; Green, J. LiDAR remote sensing of biophysical properties of tolerant northern hardwood forests. Can. J. Remote Sens. 2003, 29, 658–678. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Snowdon, P. A ratio estimator for bias correction in logarithmic regressions. Can. J. For. Res. 1991, 21, 720–724. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T. Inference for LiDAR-assisted estimation of forest growing stock volume. Remote Sens. Environ. 2013, 128, 268–275. [Google Scholar] [CrossRef]
- Ståhl, G.; Holm, S.; Gregoire, T.G.; Gobakken, T.; Næsset, E.; Nelson, R. Model-based inference for biomass estimation in a LiDAR sample survey in Hedmark County, Norway. Can. J. For. Res. 2011, 41, 96–107. [Google Scholar] [CrossRef]
- Stoltzenberg, R.M. Multiple regression analysis. In Handbook of Data Analysis; Hardy, M.A., Bryman, A., Eds.; SAGE Publications Ltd: London, UK, 2009; pp. 165–207. [Google Scholar]
- Ghosh, M.; Meeden, G. Bayesian Methods for Finite Population Sampling; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Vincent, G.; Sabatier, D.; Blanc, L.; Chave, J.; Weissenbacher, E.; Pélissier, R.; Fonty, E.; Molino, J.F.; Couteron, P. Accuracy of small footprint airborne LiDAR in its predictions of tropical moist forest stand structure. Remote Sens. Environ. 2012, 125, 23–33. [Google Scholar] [CrossRef]
- Nord-Larsen, T.; Schumacher, J. Estimation of forest resources from a country wide laser scanning survey and national forest inventory data. Remote Sens. Environ. 2012, 119, 148–157. [Google Scholar] [CrossRef]
- Chen, Q.; Vaglio Laurin, G.; Valentini, R. Uncertainty of remotely sensed aboveground biomass over an African tropical forest: Propagating errors from trees to plots to pixels. Remote Sens. Environ. 2015, 160, 134–143. [Google Scholar] [CrossRef]
- Rahlf, J.; Breidenbach, J.; Solberg, S.; Næsset, E.; Astrup, R. Comparison of four types of 3D data for timber volume estimation. Remote Sens. Environ. 2014, 155, 325–333. [Google Scholar] [CrossRef]
- Gregoire, T.G.; Næsset, E.; Ståhl, G.; Andersen, H.-E.; Gobakken, T.; Ene, L.; Nelson, R.F.; McRoberts, R.E. Statistical rigor in LiDAR-assisted estimation of aboveground forest biomass. Remote Sens. Environ. 2015. submitted. [Google Scholar]
- D’Oliveira, M.V.N.; Reutebuch, S.E.; McGaughey, R.J.; Andersen, H.E. Estimating forest biomass and identifying low-intensity logging areas using airborne scanning LiDAR in Antimary State Forest, Acre State, Western Brazilian Amazon. Remote Sens. Environ. 2012, 124, 479–491. [Google Scholar] [CrossRef]
- Meng, X.L.; Currit, N.; Zhao, K.G. Ground filtering algorithms for airborne LiDAR data: A review of critical issues. Remote Sens. 2010, 2, 833–860. [Google Scholar] [CrossRef]
- Neeff, T.; Dutra, L.V.; dos Santos, J.R.; Freitas, C.D.C.; Araujo, L.S. Tropical forest measurement by interferometric height modeling and P-band radar backscatter. For. Sci. 2005, 51, 585–594. [Google Scholar]
- Mauya, E.; Norwegian University of Life Sciences, Ås, Norway. Personal communication, 19 January 2015.
- Gobakken, T.; Næsset, E. Assessing effects of laser point density, ground sampling intensity, and field sample plot size on biophysical stand properties derived from airborne laser scanner data. Can. J. For. Res. 2008, 38, 1095–1109. [Google Scholar] [CrossRef]
- Næsset, E. Effects of different sensors, flying altitudes, and pulse repetition frequencies on forest canopy metrics and biophysical stand properties derived from small-footprint airborne laser data. Remote Sens. Environ. 2009, 113, 148–159. [Google Scholar] [CrossRef]
- Hansen, E.; Gobakken, T.; Næsset, E. Effects of pulse density on digital terrain models and canopy metrics using airborne laser scanning in a tropical rainforest. Remote Sens. 2015, 7, 8453–8468. [Google Scholar] [CrossRef] [Green Version]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hansen, E.H.; Gobakken, T.; Solberg, S.; Kangas, A.; Ene, L.; Mauya, E.; Næsset, E. Relative Efficiency of ALS and InSAR for Biomass Estimation in a Tanzanian Rainforest. Remote Sens. 2015, 7, 9865-9885. https://doi.org/10.3390/rs70809865
Hansen EH, Gobakken T, Solberg S, Kangas A, Ene L, Mauya E, Næsset E. Relative Efficiency of ALS and InSAR for Biomass Estimation in a Tanzanian Rainforest. Remote Sensing. 2015; 7(8):9865-9885. https://doi.org/10.3390/rs70809865
Chicago/Turabian StyleHansen, Endre Hofstad, Terje Gobakken, Svein Solberg, Annika Kangas, Liviu Ene, Ernest Mauya, and Erik Næsset. 2015. "Relative Efficiency of ALS and InSAR for Biomass Estimation in a Tanzanian Rainforest" Remote Sensing 7, no. 8: 9865-9885. https://doi.org/10.3390/rs70809865
APA StyleHansen, E. H., Gobakken, T., Solberg, S., Kangas, A., Ene, L., Mauya, E., & Næsset, E. (2015). Relative Efficiency of ALS and InSAR for Biomass Estimation in a Tanzanian Rainforest. Remote Sensing, 7(8), 9865-9885. https://doi.org/10.3390/rs70809865