Derivation of Sea Surface Wind Directions from TerraSAR-X Data Using the Local Gradient Method

Abstract

Derivation of sea surface wind direction is a key step of sea surface wind retrieval from spaceborne Synthetic Aperture Radar (SAR) data. This technical note describes an implementation of the Local Gradient (LG) method to derive sea surface wind directions at a scale of a few kilometers from X-band spaceborne SAR TerraSAR-X (TS-X) data in wide swath mode. The 180° ambiguity in the derived sea surface wind direction is automatically eliminated using a single reference wind direction from external data sources. Several typical cases acquired in the North Sea were presented to demonstrate the derivation of sea surface wind direction under different wind situations using this method. The derived sea surface wind direction were further compared to atmospheric model prediction results. In addition, a practical method is introduced to address ambiguity in the derived sea surface wind directions using the LG method in a typhoon case with rotating surface wind structure. By interpolating the derived wind directions at a scale of kilometers, sea surface wind speeds with a spatial resolution of 500 m are subsequently retrieved using the X-band SAR sea surface wind Geophysical Model Function (GMF). The approach accomplished by combining the LG method with the X-band GMF for deriving sea surface wind in high spatial resolution demonstrates its potential for operational service.

1. Introduction

Measurements of sea surface winds are greatly needed for marine environmental monitoring, severe weather forecasting and air-sea interaction research. In situ measurements using ships, buoys, shore-based stations and other sources are the most accurate ways to obtain sea wind information, but they are associated with drawbacks, such as high cost and coarse spatial coverage, considering the large scale of the ocean. At present, microwave scatterometers, e.g., ASCAT-A/B [1,2], HY-2 [3], Oceansat-2 [4], the full-polarimetric radiometer on WindSat [5], radar altimeters [6,7] and Synthetic Aperture Radar (SAR), are the primary remote sensing sensors that can be used to obtain all-weather and global coverage sea wind information. Each of the abovementioned types of wind sensors has advantages, as well as drawbacks. Spaceborne radar altimeters are able to yield sea surface wind speeds in global oceans, but not wind vectors. Scatterometers and radiometers can globally measure sea surface wind vectors (wind speed and wind direction) with spatial resolutions of 25–50 km. However, this relatively sparse resolution limits scatterometry to investigations of the variability in sea surface winds in coastal zones. In contrast, SAR is capable of obtaining sea surface wind information at high spatial resolutions on a kilometer scale.

With respect to sea surface wind retrieval using spaceborne SAR, the most often used methodology is to apply the Geophysical Model Function (GMF), which was originally developed for scatterometers to derive wind vectors. For example, CMOD4 [8] and CMOD5 [9] are the two major C-band GMFs adapted to C-band SARs with vertical-vertical (VV) polarization, e.g., ERS/SAR and ENVISAT/Advanced SAR (ASAR). When dealing with C-band SAR Horizontal-Horizontal (HH) polarized data, the polarization ratio model [10,11] and the CMOD GMFs are used together to retrieve sea surface wind fields. A more precise development is a dedicated GMF for SAR HH data, e.g., the one proposed in [12] for Radarsat-1 data. In addition to the widely-exploited methodology of using a GMF to derive sea surface wind fields from SAR data, other novel approaches, e.g., the linear method [13] based on SAR cross polarization data and the Doppler approach [14] based on SAR complex data, can be used to derive sea surface wind fields at high spatial resolutions from SAR data.

A major obstacle in deriving sea surface wind fields from SAR data using GMFs is that wind directions and speeds cannot be retrieved at the same time, because SAR sensors have only a single antenna, unlike scatterometers, which have multiple beams. Therefore, sea surface wind directions must first be acquired to retrieve sea surface wind fields from spaceborne SAR data. Wind directions from Numerical Weather Prediction (NWP) models are commonly used for operational sea surface wind retrieval from spaceborne SAR, e.g., presented in [15]. The major difficulty in using NWP wind directions for SAR sea surface wind retrievals is the spatial resolution, which is on a scale of tens of kilometers and is relatively coarse compared to the desired spatial resolution from SAR. Alternatively, visible wind streaks in SAR images are indications of sea surface wind direction [16]. It is generally accepted that the wind streaks presented in SAR images are induced by roll vortices in the marine atmospheric boundary layer [17,18], and it is assumed that the wind streaks are aligned with the sea surface wind directions. There are generally two methods available to derive sea surface wind directions from SAR imagery depending on these visible wind streaks. One method is the Fast Fourier Transform (FFT) method [19] applied in the frequency domain, because the sea surface wind direction is perpendicular to the FFT spectral peaks of the wind streaks. The second method, Local Gradient (LG) [20], is applied in the spatial domain. The rationale of the LG method is that the wind direction is orthogonal to the gradient direction, which indicates the strongest variation in the wind streaks. The LG method has been successfully applied to ERS/SAR and ENVISAT/ASAR data [20,21,22].

Our previous studies on sea surface wind retrieval from the X-band spaceborne SAR TerraSAR-X (TS-X) focused on the development of a GMF [23] and on mapping coastal sea surface winds [24,25,26]. The FFT method is used to derive sea surface wind directions from TS-X data in the abovementioned studies. As mentioned above, the most convenient way to operationally derive sea surface wind fields from spaceborne SAR data is to use the atmospheric model wind directions as inputs. However, because wind streaks, which can yield true wind directions, often appear in SAR images, one still would like to exploit this information in SAR images instead of only using model predictions. The previous study [21] indicated that the LG method may yield more realistic results of deriving sea surface wind direction compared to the FFT method. Therefore, in this study, we attempted to adapt the LG method to TS-X data to derive sea surface wind directions and subsequently retrieve sea surface wind speeds using XMOD2 [23] to enable the advancement of operational X-band spaceborne SAR sea surface wind measurements.

Several typical cases with different weather conditions are presented to demonstrate the efficiency of the LG method to derive sea surface wind directions from TS-X data in wide swath mode. All of the presented cases were acquired in the open sea, where the wind streaks are clearly visible, but there are no other clues that indicate the true wind directions. Therefore, our implementation of the LG method to TS-X data also includes a process for automatically eliminating the 180° ambiguity in the derived sea surface wind directions by using a single reference wind direction. Typhoon Ma-On, which was observed by TS-X, is a more complex case; the typhoon has a rotating sea wind structure, and therefore, a single reference wind direction was insufficient to eliminate the 180° ambiguity. Based on the spiral structure of tropical cyclones, simulated reference wind directions are used to resolve the true wind directions.

Following the Introduction, in Section 2, the SAR data that were utilized and the comparison dataset are described. The implementation of the LG method on TS-X data to derive sea surface wind directions is described in Section 3. The retrieved wind directions were used as inputs to XMOD2 to obtain the sea surface wind field at a high spatial resolution, which is discussed in Section 4. Comparisons between the SAR wind retrievals using the numerical model results are also presented in Section 4. The summary and conclusions are presented in the last section.

2. Description of the Dataset

The TS-X satellite was launched on 15 June 2007. The satellite operates in the X-band at a wavelength of 3.1 cm (frequency of 9.6 GHz). Its twin, TanDEM-X (TerraSAR-X add-on for Digital Elevation Measurement, TD-X), was launched in 2010. The satellites can operate either in a “communication” mode, i.e., bistatic or pursuit monostatic mode, or they can acquire data independently. TS-X and TD-X can operate in the SpotLight (SL), Stripmap (SM) and ScanSAR (SC) modes. From July 2013, Staring SpotLight and Wide ScanSAR modes were provided. In this study, TS-X and TD-X data acquired using the SC mode at VV polarization were used to retrieve sea surface wind fields. The SC mode can image the sea surface with a swath width of 100 km. The nominal pixel sizes of the TS-X SC data are 8.25 m, in both the azimuth and range directions. Therefore, the SC data are particularly suitable for mapping sea surface wind fields in regional seas because of their large coverage and high spatial resolutions.

The regional sea surface wind and wave prediction model EWAM (European Wave Model), which was provided by the German Met Service (DWD: Deutscher Wetterdienst), was used for comparisons with the SAR sea surface wind retrievals. The EWAM model data grid sizes are 0.1° × 0.05° in latitude and longitude, are available every three hours and cover the North Sea and the Baltic Sea between 50° N–65° N and −10° W–15° E. The sea surface wind fields at a height of 10 m used to drive the EWAM wave model were derived from the COSMO_EU atmospheric model (Thomas Bruns, personal communication).

3. Methodology

Details of the LG method used for deriving sea surface wind directions from ERS/SAR images have been presented by Koch [20]. In the following, some of the key steps for implementing the LG method with TS-X data are described, and the technical details are given in the Appendix.

3.1. Pre-Processing Of TS-X Data

Two steps are performed in the pre-processing part. First, the TS-X images are radiometrically calibrated. The second step is spatial smoothing to restrain the effects of speckle in the SAR images and to reduce the interference of surface wave patterns, which often coexist with wind streaks, but are at different spatial scales, on the calculation of the sea surface wind directions.

3.1.1. Radiometric Calibration of SAR Data

The TS-X data are radiometrically calibrated using:

$${\mathsf{\sigma }}^0=K_s·\left({\text{DN}}^2-\text{NEBN}\right)$$

(1)

where $K_s$ is the calibration constant and $\text{NEBN}$ is the noise equivalent beta naught of the TS-X Level 1b product. $K_s$ and $\text{NEBN}$ are provided in the TS-X metadata. DN refers to the digital number of the TS-X data.

3.1.2. Spatial Sampling

Although the LG method is based on visible wind streaks, which is a atmospheric process, the method is still mathematical. Therefore, the method can eventually find a maximum gradient regardless of whether it is induced by wind streaks or other linear patterns imaged by a SAR. Sea surface wave patterns that appear in SAR images are the strongest interference, which is somehow similar to wind streaks, but on different spatial scales. The wavelengths of sea surface waves (mainly swell) imaged by spaceborne SAR are generally between 150 m and 600 m, whereas the sea wind streak wavelengths are on the order of 2–10 km. The TS-X SC mode image shown in Figure 1 is taken as an example to illustrate the different spatial scales of the wind streaks and sea surface waves. The image was acquired over the North Sea on 18 July 2012 at 17:28 UTC. The sub-image superimposed on the upper right shows a 20 km × 20 km area where wind streaks are clearly visible and are oriented southwest-northeast. The sub-image on the lower right shows a 4 km × 4 km area with obvious swell patterns that are oriented northwest-southeast. Because their spatial scales are different, spatial smoothing can be effectively used to eliminate sea surface wave interference when calculating the local maximum gradients induced by wind streaks. Generally, within a reasonable range, the sea surface wave interference is removed more effectively as the smoothing factor increases. However, there is a tradeoff, because the spatial resolution of the derived sea surface wind direction is consequently reduced. Based on numerous experiments conducted using TS-X SC and Wide SC data, the ideal resampled pixel sizes for wind streak extraction using the LG method range from 100 m to 400 m.

Figure 1. A TerraSAR-X (TS-X) ScanSAR (SC) image acquired on 18 July 2012 at 17:28 UTC over the North Sea. The sub-image on the upper right shows wind streaks that are oriented southwest-northeast, and the sub-image in the lower-right panel shows ocean swell patterns that are oriented northwest-southeast.

Figure 1. A TerraSAR-X (TS-X) ScanSAR (SC) image acquired on 18 July 2012 at 17:28 UTC over the North Sea. The sub-image on the upper right shows wind streaks that are oriented southwest-northeast, and the sub-image in the lower-right panel shows ocean swell patterns that are oriented northwest-southeast.

A series of smoothing operators, named $R_{|2}$, are used to reduce the images to half size, to enlarge the pixel size by a factor of two. The definition of the smoothing operator is given in Equation (A1) in the Appendix. In this study, the order of the smoothing operator is fixed at 4 for the North Sea cases. Therefore, the pixel size increases from 8.25 m to 132 m after 4 times of half-size reductions (${R_{|2}}^4$). However, in the typhoon case presented later, in which long swells appear in the SAR image, an additional smoothing step is required. When using different TS-X image modes, the number of half size reductions depends on the original pixel size. As mentioned above, the re-sampled pixel size should range from 100 m to 400 m for further processing.

3.2. Extraction of Sea Surface Wind Direction

After pre-processing, the LG method is applied to derive the sea surface wind direction from the TS-X data. The TS-X SC mode image shown in Figure 1 is taken as an example to illustrate the process of extracting sea surface wind direction using the LG method. A sub-image with a spatial coverage of 10 km × 10 km is used to demonstrate how the LG is calculated and how the sea surface wind direction is subsequently derived.

3.2.1. Computation of the Local Gradient

The local gradients are computed from the sub-image using the optimized Sobel operator $D_x$ and its transpose $D_y$, which are defined in Equations (A5) and (A6), respectively, in the Appendix. The gradient is calculated in the $x$ and $y$ directions, which correspond to the SAR range and azimuth directions. A complex number therefore can help illustrate the gradient distribution more easily by using the real and imaginary parts for the x and y directions, respectively:

$$G^{\prime }=\left(D_x+i{D}_y\right)\left(A\right)$$

(2)

where $A$ is the SAR image taken as a matrix and $G^{\prime }$ is a complex matrix. Next, the complex numbers are squared; hence, any gradient and its negative value will yield the same results and can be smoothed by $R_{|2}$ Equation (A8). The square operation is undone later by taking the square root.

$$G^{″}=R_{|2}({G^{\prime }}^2)$$

(3)

Prior to determining the main direction of the gradient, quality controls are applied. Two quality measurements of $c$ and $r$ are computed from the magnitudes of the squared gradient:

$$G^{‴}=R_{|2}(|{G^{\prime }}^2|)$$

(4)

$$0\le c=\frac{\left|G^{″}\right|}{G^{‴}}\le 1\text{ and}$$

(5)

$$0\le \mathrm{r}=\frac{\left|G^{″}\right|}{\left|G^{″}\right|+Average\left(\left|G^{″}\right|\right)}\le 1$$

(6)

where $|{G^{\prime }}^2|$ and $\left|G^{″}\right|$ are the moduli of ${G^{\prime }}^2$ and $G^{″}$. $Average\left(\left|G^{″}\right|\right)$ is the mean of all $\left|G^{″}\right|$ in the sub-image. The median value is used in [20], but our experiments suggest that the mean (average) value is computationally more efficient and yields similar results.

Finally, $G_f$, which is used to derive the main direction as described in the following sub-section, is obtained from the normalized complex numbers that are weighted by the two parameters in Equations (5) and (6):

$$0\le \mathrm{r}=\frac{\left|G^{″}\right|}{\left|G^{″}\right|+Average\left(\left|G^{″}\right|\right)}\le 1$$

(7)

3.2.2. Extraction of the Main Direction

Figure 2 shows the distribution of all of the complex numbers in $G_f$. Because the complex numbers can be located in any of the four quadrants, $G_f$ is distributed in the range 0°–360° according to the gradients of the complex numbers. Thus, the entire directional plane is divided equally into 72 bins, i.e., each bin is 5° to obtain the histogram of $G_f$. Regarding the selection of the number of intervals, too few intervals will reduce the accuracy of the derived wind direction, and too many intervals will increase the random errors. A bin size of 5° is optimal according to Koch’s study [20] and our experiments. All of the complex numbers in the same interval are summed to one complex number, whose magnitude is shown by the y-axis of the histogram image in Figure 3. The histogram is further smoothed to reduce random errors using the operators$B_{8x}^2, B_{4x}^2, B_{2x}^2 \text{and }{B}_x^2$, which are defined in Equations (A6)–(A9) in the Appendix. Then, the bin of the maximum smoothed histogram is determined. The square root of the complex number in the maximum bin gives the direction of the maximum local gradient, and its orthogonal direction indicates the wind direction with a 180° ambiguity.

There are two general methods for eliminating the 180° ambiguity. When the SAR images are acquired over coastal zones, wind shadows or other clues that are often visible can indicate the true sea surface wind direction, and no external information is needed. However, in the open sea, there is generally no indication of the true wind direction. Under such conditions, collocated spatio-temporal numerical weather prediction results or other satellite measurements, e.g., by scatterometer or radiometer, can also be used to eliminate the 180° ambiguity. In our study, for rather consistent sea surface winds, we resolved the ambiguous wind direction by inputting only a single reference wind direction from the EWAM model, which is of great importance for operational SAR ocean wind service, as better results can be achieved using less external data. As an example, Figure 4a shows the derived wind direction with a 180° ambiguity at a spatial resolution of 20 km × 20 km from the TS-X image presented in Figure 1. Figure 4b shows the resolved wind direction by inputting the single reference wind direction given by the EWAM model.

Figure 2. Distribution of the complex numbers in $G_f$.

Figure 2. Distribution of the complex numbers in $G_f$.

Figure 3. The histogram and the smoothed histogram of $G_f$ derived from the sub-image shown in Figure 1.

Figure 3. The histogram and the smoothed histogram of $G_f$ derived from the sub-image shown in Figure 1.

Figure 4. (a) The derived sea surface wind direction with a 180° ambiguity using the local gradient (LG) method applied to the TS-X case acquired on 18 July 2012; (b–d) the resolved sea surface wind directions at spatial resolutions of 20 km, 10 km and 5 km, respectively, using a single reference wind direction from the European Wave Model (EWAM) model to eliminate the 180° ambiguity.

Figure 4. (a) The derived sea surface wind direction with a 180° ambiguity using the local gradient (LG) method applied to the TS-X case acquired on 18 July 2012; (b–d) the resolved sea surface wind directions at spatial resolutions of 20 km, 10 km and 5 km, respectively, using a single reference wind direction from the European Wave Model (EWAM) model to eliminate the 180° ambiguity.

The scale of sea surface wind streaks ranges from 2 km to 10 km; therefore, the size of sub-images for extracting the main gradient should be generally no less than 10 km to maintain a robust process. Figure 4c shows the resolved sea surface wind direction within each 10 km × 10 km sub-image, and the sea surface wind direction at a higher spatial resolution of 5 km × 5 km is shown in Figure 4d. For both cases, only a single reference wind direction provided by the EWAM model is used to eliminate the 180° ambiguity. The results are quite consistent with the visible wind streaks in the TS-X SC image, except for a few disagreements that can be seen in Figure 4d. The retrieved sea surface wind field in this case and its comparison with the EWAM model are presented in detail in the next section.

Extracted wind directions from TS-X data using the LG method at spatial resolutions of 10 or 5 km still cannot satisfy the requirements of retrieving sea surface wind fields at a spatial resolution of one kilometer. Thus, a linear interpolation was used, and the interpolated sea surface wind directions are used as inputs to the X-band sea surface wind field retrieval GMF XMOD2 [23] to calculate the sea surface wind speeds. XMOD2 has the same general expression as other SAR wind GMFs, which describe the dependence of the normalized radar cross-section (NRCS) on sea surface wind and radar geometry as:

$${\sigma }_0=B_0\left(v,\theta \right)\left(1+B_1\left(v,\theta \right)cos\varnothing +B_2\left(v,\theta \right)cos2\varnothing \right)$$

(8)

where ${\mathsf{\sigma }}_0$ is the NRCS in linear units, $\mathsf{\theta }$ is the incident angle and $\mathrm{v}$ and $\mathsf{\phi }$ are the sea surface wind speed and direction, respectively. $\varnothing$ is the relative wind direction, which is defined as the angle between the radar-looking direction $\alpha$ and the true wind direction $\phi$ $(\varnothing =\phi -\alpha )$.

4. Case Studies

In this section, several representative cases with sea wind conditions, including homogeneous sea surface winds, convective cells and a tropical cyclone (typhoon), are presented to demonstrate the application of the LG method to TS-X data and the automatic elimination of the 180° ambiguity in the derived sea surface wind direction.

4.1. General Cases

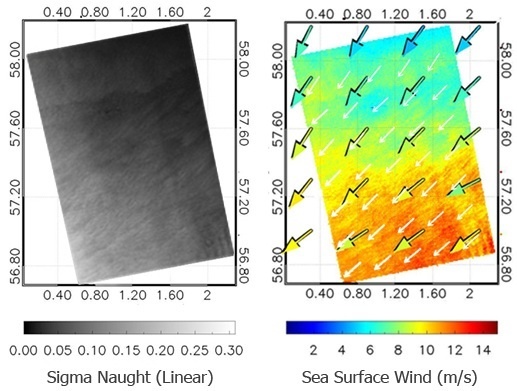
4.1.1. A Homogeneous Sea Surface Wind Case

Figure 5 presents the sea surface wind field retrieved from the TS-X SC image shown in Figure 1. The sea surface wind speed at a spatial resolution of 500 m was retrieved using the derived sea surface wind direction at 10 km, as shown in Figure 4c. The superimposed color-coded arrows show the spatially-collocated EWAM model sea surface wind field at 18:00 UTC on 18 July 2012, which is approximately a half hour later than the TS-X acquisition. The comparison indicates that the derived sea surface wind directions agree well with the model results, whereas the retrieved sea surface wind speed from the TS-X data are 2–3 m/s greater than the model results in the southern part of the image.

Figure 5. Comparison of the retrieved sea surface wind field from the TS-X data acquired on 18 July 2012 at 17:28 UTC with the EWAM wind model result at 18:00 UTC. The white arrows indicate the retrieved sea surface wind directions from the TS-X data using the LG method, and the EWAM sea surface wind vectors are represented by the color-coded arrows.

Figure 5. Comparison of the retrieved sea surface wind field from the TS-X data acquired on 18 July 2012 at 17:28 UTC with the EWAM wind model result at 18:00 UTC. The white arrows indicate the retrieved sea surface wind directions from the TS-X data using the LG method, and the EWAM sea surface wind vectors are represented by the color-coded arrows.

4.1.2. An Extra-Tropical Cyclone Case

Figure 6a shows a TS-X SC image acquired over the North Sea on 12 July 2012 at 17:37 UTC, which shows a large spatial variation in the sea surface radar backscatter. The EWAM model result at 18:00 UTC and the radiometer WindSat measurement at 16:36 UTC suggest that a cyclone was approaching the west coast of Denmark and Germany, although the magnitude of the maximum sea surface wind speed was only approximately 15 m/s. Thus, the large dark feature close to the center of the cyclone in the TS-X image indicates the area of low sea surface wind speeds. The derived sea surface wind directions shown in Figure 6b (white arrows) change from approximately 135° furthest from the center to 175° in the low wind speed area, which agrees well with the EWAM model wind directions, particularly outside the center of the cyclone. Close to the center of the cyclone, the radar backscatter, which was down to be approximately −20 dB, may have induced errors in the calculation of the local gradient. The retrieved sea surface wind speed varies significantly from approximately 10 m/s on the outside to 3 m/s in the center of the cyclone. We can observe that there is a spatial displacement between the TS-X wind speed retrieval and the EWAM model result, which is due to the fast southeastward movement of the cyclone during the half hour interval between the TS-X acquisition and model output times.

Figure 6. (a) A TS-X SC image acquired on 12 July 2012 at 17:37 UTC over the North Sea and (b) the comparison of the TS-X retrieved sea surface wind field with the EWAM model result at 18:00 UTC.

Figure 6. (a) A TS-X SC image acquired on 12 July 2012 at 17:37 UTC over the North Sea and (b) the comparison of the TS-X retrieved sea surface wind field with the EWAM model result at 18:00 UTC.

4.1.3. A Convective Cell Case

Convective cells are defined as quasi-two-dimensional organized large eddies, which are basically caused by well-defined mean flows or dynamic instabilities in general shearing and turning velocity profiles [27,28]. The convective cells can change the sea surface roughness, which changes the radar backscatter. The spatial scale of convective cells is 1 km–10 km, depending on the properties of the marine atmospheric boundary layer [29].

Figure 7a shows a TS-X SC image acquired on 18 May 2012 at 17:36 UTC over the North Sea. The superimposed sub-image clearly indicates the occurrence of convective cells, which appear as bubble-like features. The derived sea surface wind directions at a spatial resolution of 10 km are represented by the white arrows in Figure 7b and are in very good agreement with the EWAM model result at 18:00 UTC, which has a time lag of 24 min. In the upper panel of the TS-X image, some bright and dark patches are visible, which are particularly clearly represented in the retrieved sea surface wind map and contrast with the ambient sea surface wind. These patches indicate that rain was probably falling when the TS-X data were acquired, which thereby could have induced a bias in the retrieved sea surface wind speeds, and as we can observe, the discrepancies in the sea surface wind speeds between the TS-X retrieval and EWAM model result occur mainly in the northern part of the area.

Figure 7. (a) A TS-X SC image acquired on 18 May 2012 at 17:36 UTC over the North Sea and (b) the comparison of the TS-X retrieved sea surface wind field with the EWAM model results at 18:00 UTC.

Figure 7. (a) A TS-X SC image acquired on 18 May 2012 at 17:36 UTC over the North Sea and (b) the comparison of the TS-X retrieved sea surface wind field with the EWAM model results at 18:00 UTC.

4.1.4. Verification of the TS-X Retrieved Sea Surface Wind Directions

For the three cases presented above, quantitative comparisons of the sea surface wind directions derived from the TS-X data using the LG method with the EWAM model results are given. All of the derived sea surface wind directions are at a spatial resolution of 10 km, which were spatially collocated with the EWAM model results for comparison. There are 350 data pairs from the three cases. The scatter diagram shown in Figure 8 suggests that the derived sea surface wind directions from TS-X are in good agreement with the model predictions, with a bias of 0.93° and a root mean square error (RMSE) of 13.59°.

Figure 8. Scatterplot of the wind directions from the EWAM model and the retrieved wind directions from TS-X/ TanDEM-X (TD-X) using the LG method.

Figure 8. Scatterplot of the wind directions from the EWAM model and the retrieved wind directions from TS-X/ TanDEM-X (TD-X) using the LG method.

4.2. A Tropical Cyclone Case

In each of the three cases presented above, a single reference wind direction from the EWAM model results was used to effectively eliminate the 180° ambiguity in the derived sea surface wind directions when the TS-X images are acquired over the open sea and when there are no clear clues to resolve the wind direction. However, this model is not suitable for complicated sea surface winds. In the following, a typhoon case is presented to demonstrate a practical method for eliminating the 180° ambiguity of the complicated wind conditions of a tropical cyclone.

Wind fields in typhoons generally have spiral structures. Akin to the methodology developed by Holland [30] to simulate the sea surface wind field of tropical cyclones, we developed a simple, but robust method to automatically eliminate the ambiguity in the derived wind directions for typhoon cases. The method uses the relative position of the typhoon eye and the sea surface wind directions. The typhoon eye can be regarded as the center of a spiral. The wind direction is approximately 20°–25° [31] counter clockwise in the North Hemisphere and clockwise in the South Hemisphere, relative to the tangential direction of the spiral line, as illustrated in Figure 9. Therefore, we can automatically simulate reference wind directions for each sub-image when the typhoon eye is manually identified in the TS-X image.

Figure 9. Sketch of the relationship between the typhoon eye and sea surface wind directions.

Figure 9. Sketch of the relationship between the typhoon eye and sea surface wind directions.

Figure 10a shows the TS-X SC image acquired over the typhoon Ma-On on 17 July 2011 in the west Pacific. The TS-X image clearly shows a typical typhoon spiral structure where the apparent wind streaks rotate around the typhoon’s eye. Unlike the cases presented above, the pixel size was re-sampled from 8.25 m to 264 m using a smoothing factor of five because long swells generated by the typhoon were also imaged by TS-X. The abovementioned method of simulating reference wind directions is used to eliminate the 180° ambiguities in the derived wind directions. The derived sea surface wind directions at a spatial resolution of 10 km are shown in Figure 10a, and the retrieved sea surface wind speeds using XMOD2 are shown in Figure 10b. The maximum retrieved sea surface wind speed is approximately 30 m/s and appears in the east-northeast quadrant of the typhoon. According to the Best Track records issued by the Japanese Meteorology Agency, the maximum sustained wind speed of typhoon Ma-On at 9:00 UTC was 43 m/s, which is much higher than the retrieved sea surface wind speed. It should be noted that XMOD2 is validated for sea surface wind speeds up to 25 m/s. Nevertheless, the derived sea surface wind direction appropriately represents the typhoon wind situation, whereas the performance of the X-band GMF under high winds requires further effort.

Figure 10. (a) The TS-X SC image acquired on 17 July 2011 at 08:59 UTC over typhoon Ma-On in the west Pacific and the superimposed derived sea surface wind directions using the LG method; (b) the retrieved sea surface wind field using the derived wind direction and XMOD2.

Figure 10. (a) The TS-X SC image acquired on 17 July 2011 at 08:59 UTC over typhoon Ma-On in the west Pacific and the superimposed derived sea surface wind directions using the LG method; (b) the retrieved sea surface wind field using the derived wind direction and XMOD2.

5. Conclusions

To operationally provide sea surface wind fields using spaceborne SAR, the derivation of sea surface wind directions is a key step. In this study, the local gradient method, which was originally proposed for the ERS-2/SAR data, was implemented for X-band spaceborne SAR TS-X ScanSAR data to derive sea surface wind directions. By combining the derived sea surface wind directions using the method and the previously-developed X-band GMF XMOD2, sea surface wind fields at high spatial resolutions retrieved from the TS-X/TD-X data in wide swath mode were achieved.

The case studies in the North Sea suggest that a re-sampled pixel size of approximately 150 m and a fixed sub-image size of 10 km × 10 km are appropriate for deriving sea surface wind directions using the local gradient method. Using a single reference wind direction given by a numerical weather prediction model, the 180° ambiguity is automatically eliminated. The comparison of the derived sea surface wind directions from the TS-X data using the LG method with the EWAM model predictions suggests a good agreement, with a bias of 0.93° and an RMSE of 13.59°.

Different from those cases in the North Sea, the result of the special case of typhoon Ma-On suggests that a larger smoothing factor, i.e., a re-sampled pixel size of approximately 300 m, is needed when long swells are present in SAR images. Moreover, with respect to the complicated sea surface wind field in the typhoon case, we developed a practical method to construct a reference wind direction based on the spiral structure of the typhoon wind field for each sub-image to eliminate the ambiguity.

In summary, in this study, we have thoroughly described the implementation of the local gradient method to TS-X/TD-X data, the automatic elimination of the 180° ambiguity and their combinations with XMOD2 to obtain sea surface wind fields at high spatial resolutions under different wind conditions. This study has yielded significant progress in operational sea surface wind retrievals using TS-X and TD-X data in regional seas.