Rainfall Intra-Seasonal Variability and Vegetation Growth in the Ferlo Basin (Senegal)
Abstract
:1. Introduction
2. Datasets and Methods
2.1. Study Area
- the northern sandy pastoral region (24,763 km2) where the predominant soils are red-brown sandy soils and ferruginous tropical sandy soils, covered by open shrub steppes and grasslands. On average, tree and shrub canopy cover does not exceed 5% of the total area, and the pseudo-steppe consists of a discontinuous herbaceous cover of annual grasses;
- the ferruginous pastoral region (30,908 km2) where soils are mainly shallow loamy and gravelly ferruginous tropical soils and lithosols on the plateau, and deep, sandy-to-loamy, leached tropical ferruginous soils in the valleys, the vegetation being characterized by shrub savanna, and bushland, often relatively dense. The herbaceous layer comprises a mix of annual and perennial grasses, leguminous species and other plants;
- the southern sandy pastoral region (10,852 km2) where the predominant soils are ferruginous tropical sandy soils, slightly leached, and covered by shrubs and tree savanna. In the wetter, southern part of the region, species diversity increases and the tree species become more abundant [14]. The herbaceous layer is dominated by leguminous species.

| Soils | Description |
|---|---|
| Ferruginous Tropical soils | Found on the western and southern part with a sandy and clayey-sandy texture; they have a red color and are poor in organic matter. The soil surface is degraded as a result of exploitation and the absence of fallow periods. They usually have a low level of organic matter. |
| Hydromorphic soils | Found in the Ferlo valley and its former tributaries, they have variable textural features ranging from sandy silt to clayey silt. Their development is linked to a slight deficiency of drainage, which allows a certain accumulation of organic material. |
| Regosols soils | Very shallow and little evolved; they generally occupy the lower slopes in association with lithosols. They have low organic matter content. |
| Lithosols soils | Cover practically all of eastern Ferlo, they are raw mineral soils formed by non-climatic erosion of hard rock. They have low organic matter content. |
| Brown Red soils | Located in northern and western Ferlo on low plateaus and fixed dunes, they are characterized by poor organic matter content and low chemical fertility, they consist mainly of sand and clay. These soils have a red-brown color with low organic matter content uniform over much of the profile. |
| Vegetation Type | North to Center Ferlo | South Ferlo |
|---|---|---|
| Tree and bush species | Acacia seyal | Guiera senegalensis |
| Combretum micrathum (kinkéliba) | Combretum glutinosum | |
| C. glutinosum | ||
| C. nigricans | ||
| Pterocarpus lucens | ||
| Guiera senegalensis | ||
| Feretia apodanthera | ||
| Grewia bicolor | ||
| Pterocarpus lucens | ||
| Herbaceous species | Dactyloctenium aegyptium, | Zornia glochidiata Reichb |
| Aristida mutabilis | Alysicarpus ovalifolius | |
| Cenchrus biflorus | Indigofera senagalensis | |
| Schoenefeldia gracilis | ||
| Tribulis terrestris | ||
| Cassia obtifolius | ||
| Zornia glochidiata. |
2.2. Satellite Data
2.2.1. LAI
2.2.2. Rainfall
2.2.3. Soil Moisture
2.3. Methodology
2.3.1. Surface Classification
Land Cover
Homogeneous-Zone Characterization

| Abbreviation | Description |
|---|---|
| TSvS-L1 | Tree-Savanna with Shrubs (TSvS) on lithosols Soils (L) |
| TSv-L | Tree-Savannah (TSv) on lithosols Soils (L) |
| TSvS-L2 | Tree-Savanna with Shrubs (TSvS) on Lithosols soils (L) |
| TSvS-F1 | Tree-Savanna with Shrubs (TSvS) on Ferruginous tropical soils (F) in southeast sub-region |
| TSvS-L3 | Tree-Savanna with Shrubs (TSvS) on Lithosols soils (L) |
| TSvS-R | Tree-Savanna with Shrubs (TSvS) on Regosol soils (R) |
| TSvS-F2 | Tree-Savanna with Shrubs (TSvS) on Ferruginous tropical (F) in northwest sub-region |
| TSvS-RB | Tree-Savanna with Shrubs (TSvS) on Red-Brown soils (RB) |
| SStT-F | Shrub-Steppe with Trees (SStT) on Ferruginous tropical (F) |
2.3.2. Vegetation Phenology Parameters
2.3.3. Soil Moisture
2.3.4. Rainfall Parameters
2.3.5. Comparison of TRMM3B42 and RFE 2.0 Products


2.3.6. Use of the Satellite-Derived Soil Moisture for Depicting the Intra-Seasonal Rainfall Variation


3. Mean Patterns of the Rainfall and Vegetation Phenology


4. Intra-Seasonal Analysis of Vegetation Response
4.1. Effect of Rainfall Anomalies on LAI Variations through the Season

4.1.1. Positive Anomalies (Rainfall or SM above the Mean)
4.1.2. Negative Anomalies (Rainfall or SM below the Mean)
4.2. Impacts of Within-Season Rainfall and SM Variability on LAI
- -
- Is the vegetation phenology (delay, amplitude) sensitive to the rainfall onset date?
- -
- Do the variations in the total rainfall amount have a similarly effect on all VSZs, and do the dry spells have a similar effect on the vegetation growth, whatever their date, number and duration?
4.2.1. Rainy-Season Onset
4.2.2. Rainfall Amount
- -
- Total rainfall over the growing season (June–September):
- -
- Impact of dry spells
| VSZ | Correlation Coefficient | ||
|---|---|---|---|
| With TRMM | With RFE 2.0 | With SM | |
| TSvS-L1 | -- | -- | -- |
| TSv-L | -- | -- | -- |
| TSvS-L2 | -- | -- | -- |
| TSvS-F1 | 0.61 | 0.47 | 0.53 |
| TSvS-L3 | 0.56 | 0.30 | 0.32 |
| TSvS-R | 0.84 | 0.84 | 0.71 |
| TSvS-F2 | 0.68 | 0.55 | 0.64 |
| TSvS-RB | 0.82 | 0.74 | 0.79 |
| SStT-F | 0.69 | 0.77 | 0.78 |

| VSZ | Significant Correlation Coefficients | RMSE |
|---|---|---|
| SStT-F | −0.71 | 3.29 |
| TSvS-F2 | −0.79 | 3.23 |
| TSvS-F1 | −0.54 | 4.34 |
| TSvS-L3 | — | 4.31 |
| TSvS-L2 | — | 4.63 |
| TSvS-L1 | — | 4.52 |
5. Discussion
5.1. Significant Information from Rainfall and SM Products
- -
- Correlations of both positive and negative anomalies are higher for SM and RFE 2.0 than TRMM3B42, except on lithosols. In addition, the time lag obtained with SM for negative anomalies is slightly smaller than for the two rainfall products.
- -
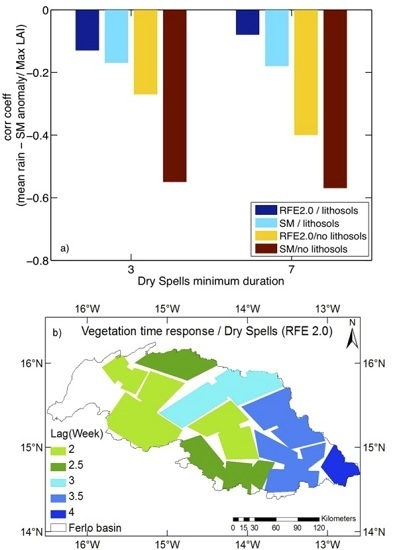
- Correlations of the cumulated water deficit, as well as the number of dry spells and the duration of the longest one, with maximum LAI were calculated to evaluate the impact of dry spells on the maximum LAI. Again, a significant correlation was found, except for lithosols. However, this correlation becomes significant for SM as soon as the dry anomaly is longer than three days, but is significant for both rainfall products only for anomalies longer than seven days. In general, a better correlation is obtained with TRMM3B42 than RFE 2.0 (for example, see the correlation for the longest dry spell).
5.2. Impact of the Intra-Seasonal Variations in the Rainy Season on the Vegetation Phenology
5.2.1. Impacts of Water Variability Across the Ferlo Basin
5.2.2. Role of Vegetation Cover and Soil Type
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lebel, T.; Ali, A. Recent trends in the Central and Western Sahel rainfall regime (1990–2007). J. Hydrol. 2009, 375, 52–64. [Google Scholar] [CrossRef]
- Herrmann, M.S.; Anyamba, A.; Tucker, J.C. Recent trends in vegetation dynamics in the African Sahel and their relationship to climate. Glob. Environ. Chang. 2005, 15, 394–404. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Farrar, T.J. The influence of soil type on the relationships between NDVI, rainfall, and soil moisture in semiarid Botswana. I. NDVI response to rainfall. Remote Sens. Environ. 1994, 50, 107–120. [Google Scholar] [CrossRef]
- Marteau, R.; Moron, V.; Philippon, N. Spatial coherence of monsoon onset over Western and Central Sahel (1950–2000). J. Clim. 2009, 22, 1313–1324. [Google Scholar] [CrossRef]
- Ibrahim, B.; Polcher, J.; Karambiri, H.; Rockel, B. Characterization of the rainy season in Burkina Faso and it’s representation by regional climate models. Clim. Dyn. 2012, 39, 1287–1302. [Google Scholar] [CrossRef] [Green Version]
- Barron, J.; Rockström, J.; Gichuki, F.; Hatibu, N. Dry spell analysis and maize yields for two semi-arid locations in east Africa. Agric. For. Meteorol. 2003, 117, 23–37. [Google Scholar] [CrossRef]
- Frappart, F.; Hiernaux, P.; Guichard, F.; Mougin, E.; Kergoat, L.; Arjounin, M.; Lavenu, F.; Koité, M.; Paturel, J.E.; Lebel, T. Rainfall regime across the Sahel band in the Gourma region, Mali. J. Hydrol. 2009, 375, 128–142. [Google Scholar] [CrossRef] [Green Version]
- Karlson, M.; Ostwald, M. Remote sensing of vegetation in the Sudano-Sahelian zone: A literature review from 1975 to 2014. J. Arid Environ. 2015, 124, 257–269. [Google Scholar] [CrossRef]
- Tarnavsky, E.; Mulligan, M.; Ouessar, M.; Faye, A.; Black, E. Dynamic hydrological modeling in drylands with TRMM based rainfall. Remote Sens. 2013, 5, 6691–6716. [Google Scholar] [CrossRef] [Green Version]
- Soti, V.; Puech, C.; lo Seen, D.; Bertran, A.; Vignolles, C.; Mondet, B.; Dessay, N.; Tran, A. The potential for remote sensing and hydrologic modelling to assess the spatio-temporal dynamics of ponds in the Ferlo Region (Senegal). Hydrol. Earth Syst. Sci. 2010, 14, 1449–1464. [Google Scholar] [CrossRef] [Green Version]
- Beven, K.J.; Fisher, J. Remote sensing and Scaling in Hydrology, Scaling in Hydrology Using Remote Sensing. In Scaling Issues in Hydrology; Stewart, J.B., Engman, E.T., Fedds, A., Kerr, Y., Eds.; Wiley: Chichester, UK, 1996. [Google Scholar]
- Gash, J.H.C.; Kabat, P.; Monteny, B.; Amadou, M.; Bessemoulin, P.; Billing, H.; Blyth, E.; DeBruin, H.; Elbers, J.; Friborg, T. The variability of evaporation during the HAPEX-Sahel Intensive Observation Period. J. Hydrol. 1997, 188, 385–399. [Google Scholar] [CrossRef]
- Zribi, M.; Pardé, M.; de Rosnay, P.; Baup, F.; Boulain, N.; Descroix, L.; Pellarin, T.; Mougin, E.; Ottlé, C.; Decharme, B. ERS scatterometer surface soil moisture analysis of two sites in the south and north of the Sahel region of West Africa. J. Hydrol. 2009, 375, 253–261. [Google Scholar] [CrossRef] [Green Version]
- Tappan, G.G.; Sall, M.; Wood, E.C.; Cushing, M. Ecoregions and land cover trends in Senegal. J. Arid Environ. 2004, 59, 427–462. [Google Scholar] [CrossRef]
- Martinez, B.; Gilabert, M.A.; Garcia-Haro, F.J.; Faye, A.; Meliά, J. Characterizing land condition variability in Ferlo, Senegal (2001–2009) using multi-temporal 1-km Apparent Green Cover (AGC) SPOT VEGETATION data. Glob. Planet. Chang. 2011, 76, 152–165. [Google Scholar] [CrossRef]
- Akpo, L.E.; Gaston, A.; Grouzis, M. Structure spécifique d’une végétation sahélienne. Cas de Wiidu Thiengoli (Ferlo, Sénégal). Bull. Mus. Natl. Hist. Nat. Paris 1995, 17, 39–52. [Google Scholar]
- Land-Cover Map from FAO 2005. Available online: http://www.glcn.org/databases/se_landcover_en.jsp (accessed on 2 September 2015).
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Yang, W.; Shabanov, N.V.; Huang, D.; Dickinson, R.E.; Nemani, R.R.; Knyazikhin, Y.; Myneni, R.B. Analysis of leaf area index products from combination of MODIS TERRA and AQUA data. Remote Sens. Environ. 2006, 104, 297–312. [Google Scholar] [CrossRef]
- De Kauwe, M.G.; Disney, M.I.; Quaife, T.; Lewis, P.; Williams, M. An assessment of the MODIS collection 5 Leaf Area Index product for a region of mixed coniferous forest. Remote Sens. Environ. 2011, 115, 767–780. [Google Scholar] [CrossRef]
- Ruhoff, A.L.; Paz, A.R.; Aragao, L.E.O.C.; Mu, Q.; Malhi, Y.; Collischonn, W.; Rocha, H.R.; Running, S.W. Assessment of the MODIS global evapotranspiration algorithm using eddy covariance measurements and hydrological modelling in the Rio Grande basin. Hydrol. Sci. J. 2013, 58, 1–19. [Google Scholar] [CrossRef]
- Yuan, H.; Dai, Y.; Xiao, Z.; Ji, D.; Shangguan, W. Reprocessing the MODIS Leaf Area Index products for land surface and climate modeling. Remote Sens. Environ. 2011, 115, 1171–1187. [Google Scholar] [CrossRef]
- LAI MODIS Product. Available online: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mod15a2 (accessed on 12 May 2015).
- Knyazikhin, Y.; Martonchik, V.; Diner, D.J.; Myneni, R.B.; Verstraete, M. Estimation of vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from atmosphere-corrected MISR data. J. Geophys. Res. 1998, 103, 32239–32256. [Google Scholar] [CrossRef]
- Bobée, C.; Ottlé, C.; Maignan, F.; de Noblet-Ducoudré, N.; Maugis, P.; Lézine, A.M.; Ndiaye, M. Analysis of vegetation seasonality in Sahelian environments using MODIS LAI, in association with land cover and rainfall. J. Arid Environ. 2012, 84, 38–50. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Liu, Z. Monitoring the response of vegetation phenology to precipitation in Africa by coupling MODIS and TRMM3B42 instruments. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Fensholt, R.; Sandholt, I.; Rasmussen, M.S. Evaluation of MODIS LAI, fAPAR and the relation between fAPAR and NDVI in a semi-arid environment using in situ measurements. Remote Sens. Environ. 2004, 91, 490–507. [Google Scholar] [CrossRef]
- Privette, J.L.; Myneni, R.B.; Knyazikhin, Y.; Mukelabai, M.; Roberts, G.; Pniel, M.; Wang, Y.; Leblanc, S. Early spatial and temporal validation of MODIS LAI product in Africa. Remote Sens. Environ. 2002, 83, 232–244. [Google Scholar] [CrossRef]
- White, M.A.; Nemani, R.R.; Thornton, P.E.; Running, S.W. Satellite evidence of phenological differences between urbanized and rural areas of the eastern United States deciduous broadleaf forest. Ecosystems 2002, 5, 260–277. [Google Scholar] [CrossRef]
- Kang, S.; Running, S.W.; Lim, J.H.; Zhao, M.; Park, C.R.; Loehman, R. A regional phenology model for detecting onset of greenness in temperate mixed forests, Korea: An application of MODIS leaf area index. Remote Sens. Environ. 2003, 86, 232–242. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM3B42 Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Xie, P.; Arkin, P.A. Analysis of global monthly precipitation using gauge observations, satellite estimates, and numerical model prediction. J. Clim. 1996, 9, 840–858. [Google Scholar] [CrossRef]
- Pierre, C.; Bergametti, G.; Marticorena, B.; Mougin, E.; Lebel, T.; Ali, A. Pluriannual comparisons of satellite-based rainfall products over the Sahelian belt for seasonal vegetation modeling. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Samimi, C.; Fink, A.H.; Paeth, H. The 2007 flood in the Sahel: Causes, characteristics and its presentation in the media and FEWS NET. Nat. Hazards Earth Syst. Sci. 2012, 12, 313–325. [Google Scholar] [CrossRef] [Green Version]
- Leduc-Leballeur, M.; de Coëtlogon, G.; Eymard, L. Air–sea interaction in the Gulf of Guinea at intraseasonal time-scales: wind bursts and coastal precipitation in boreal spring. Q. J. R. Meteorol. Soc. 2013, 139, 387–400. [Google Scholar] [CrossRef]
- Chen, Y.; Ebert, E.E.; Walsh, K.J.E.; Davidson, N.E. Evaluation of TMPA 3B42 daily precipitation estimates of tropical cyclone rainfall over Australia. J. Geophys. Res. Atmos. 2013, 118, 1–13. [Google Scholar] [CrossRef]
- Li, L.; Hong, Y.; Wang, J.; Adler, R.F.; Policelli, F.S.; Habib, S.; Korme, T.; Okello, L. Evaluation of the real-time TRMM-based multi-satellite precipitation analysis for an operational flood prediction system in Nzoia Basin, Lake Victoria, Africa. Nat. Hazards 2009, 50, 109–123. [Google Scholar] [CrossRef]
- Maidment, R.I.; Grimes, D.I.F.; Allan, R.P.; Greatrex, H.; Rojas, O.; Leo, O. Evaluation of satellite-based and model re-analysis rainfall estimates for Uganda. Meteorol. Appl. 2013, 20, 308–317. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; van Oevelen, P.; et al. The international soil moisture network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef]
- Seneviratne, S.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Taylor, C.M.; de Jeu, R.A.M.; Guichard, F.; Harris, P.P.; Dorigo, W.A. Afternoon rain more likely over drier soils. Nature 2012, 489, 423–426. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van der Molen, M.K.; Dolman, A.J.; Ciais, P.; Eglin, T.; Gobron, N.; Law, B.E.; Meir, P.; Peters, W.; Phillips, O.L.; Reichstein, M.; et al. Drought and ecosystem carbon cycling. Agric. For. Meteorol. 2011, 151, 765–773. [Google Scholar] [CrossRef]
- Bolten, J.D.; Crow, W.T. Improved prediction of quasi-global vegetation conditions using remotely-sensed surface soil moisture. Geophys. Res. Lett. 2012, 39, 1–5. [Google Scholar] [CrossRef]
- Parinussa, R.M.; de Jeu, R.A.M.; Wagner, W.W.; Dorigo, W.A.; Fang, F.; Teng, W.; Liu, Y.Y. Soil Moisture. Spec. Suppl. Bull. Am. Meteorol. Soc. 2013, 94, S24–S25. [Google Scholar]
- Wagner, W.; Dorigo, W.; de Jeu, R.; Fernandez, D.; Benveniste, J.; Haas, E.; Ertl, M. Fusion of active and passive microwave observations to create an essential climate variable data record on soil moisture. In Proceeding of the XXII ISPRS Congress on ISPRS Annals of the Photogrammetry. Remote Sensing and Spatial Information Sciences, Melbourne, Australia, 25 August–1 September 2012; Volume 1–7, pp. 315–321.
- Liu, Y.Y.; Parinussa, R.M.; Dorigo, W.A.; de Jeu, R.A.M.; Wagner, W.; van Dijk, A.I.J.M.; McCabe, M.F.; Evans, J.P. Developing an improved soil moisturedataset by blending passive and active microwave satellite-based retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 425–436. [Google Scholar] [CrossRef] [Green Version]
- ESA-CCI Soil Moisture Product Description. Available online: http://www.esa-soilmoisture-cci.org/ (accessed on 27 September 2015).
- Soil Moisture Validation from the International Soil Moisture Network. Available online: https://ismn.geo.tuwien.ac.at/ (accessed on 23 June 2015).
- Dorigo, W.A.; Gruber, A.; de Jeu, R.A.M.; Wagner, W.; Stacke, T.; Loew, A.; Albergel, C.; Brocca, L.; Chung, D.; Parinussa, R.M.; et al. Evaluation of the ESA CCI soil moistureproduct using ground-based observations. Remote Sens. Environ. 2015, 162, 380–395. [Google Scholar] [CrossRef]
- Landsat 5 Images Acquired by the TM Sensor. Available online: https://lpdaac.usgs.gov/data_access/glovis (accessed on 23 June 2015).
- Plan National d’Aménagement du Territoire. Cartographie et Télédétection des ressources naturelles du Sénégal. Etude de la Géologie, de l’hydrologie, des sols, de la Végétation et des Potentiels d’utilisation des Sols. Available online: http://library.wur.nl/isric/fulltext/ISRIC_16108.pdf (accessed on 27 September 2015).
- Jönsson, P.; Eklundh, L. Timesat: A program for analyzing time series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
- Chen, J.M.; Deng, F.; Chen, M. Locally adjusted cubic-spline capping for reconstructing seasonal trajectories of a satellite-derived surface parameter. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2230–2237. [Google Scholar] [CrossRef]
- Odekunle, T.O. Determining rainy season onset and retreat over Nigeria from precipitation amount and number of rainy days. Theor. Appl. Climatol. 2005, 83, 193–201. [Google Scholar] [CrossRef]
- Thiemig, V.; Rojas, R.; Zambrano-Bigiarini, M.; Levizzani, V.; de Roo, A. Validation of satellite-based precipitation products over sparsely gauged African river basins. J. Hydrometeorol. 2012, 13, 1760–1783. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Olson, W.S.; Yang, S.; Stout, J.E.; Grecu, M. Measuring precipitation from space. In The Goddard Profiling Algorithm (GPROF): Description and Current Applications; Levizzani, V., Bauer, P., Turk, F.J., Eds.; Springer: Berlin, Germany, 2007; pp. 179–188. [Google Scholar]
- Justice, C.O.; Townshend, J.R.G.; Holben, B.N.; Tucker, C.J. Analysis of the phenology of global vegetation using meteorological satellite data. Int. J. Remote Sens. 1985, 6, 1271–1318. [Google Scholar] [CrossRef]
- Farrar, T.J.; Nicholson, S.E.; Lare, A.R. The influence of soil type on the relationships between NDVI, rainfall and soil moisture in semiarid Botswana. II. NDVI response to soil moisture. Remote Sens. Environ. 1994, 50, 121–133. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Davenport, M.L.; Malo, A.R. A comparison of the vegetation response to rainfall in the Sahel and East Africa, using normalized difference vegetation index from NOAA AVHRR. Clim. Chang. 1990, 17, 209–241. [Google Scholar] [CrossRef]
- Wang, J.; Rich, P.M.; Price, K.P. Temporal responses of NDV to precipitation and temperature in the central Great Plains, USA. Int. J. Remote Sens. 2003, 24, 2345–2364. [Google Scholar] [CrossRef]
- Djoufack, M.V.; Brou, T.; Fontaine, B.; Tsalefac, M. Variabilité intrasaisonnière des precipitations et de leur distribution: Impacts sur le développement du couvert végétal dans le Nord du Cameroun (1982–2002). Sécheresse 2011, 22, 159–170. (In French) [Google Scholar]
- Rambal, S.; Cornet, A. Simulation de l’utilisation de l’eau et de la production végétale d’une phytocénose sahélienne du Sénégal. Acta Œcologica/ŒcologiaPlantaruni 1982, 3, 381–397. [Google Scholar]
- Mougin, E.; Hiernaux, P.; Kergoat, L.; Grippa, M.; de Rosnay, P.; Timouk, F.; le Dantec, V.; Demarez, V.; Lavenu, F.; Arjounin, M.; et al. The AMMA-CATCH Gourma observatory site in Mali: Relating climatic variations to changes in vegetation, surface hydrology, fluxes and natural resources. J. Hydrol. 2009, 375, 14–33. [Google Scholar] [CrossRef] [Green Version]
- Hiernaux, P.; le Houérou, N.H. Les parcours du Sahel. Sécheresse 2006, 17, 51–71. (In French) [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cissé, S.; Eymard, L.; Ottlé, C.; Ndione, J.A.; Gaye, A.T.; Pinsard, F. Rainfall Intra-Seasonal Variability and Vegetation Growth in the Ferlo Basin (Senegal). Remote Sens. 2016, 8, 66. https://doi.org/10.3390/rs8010066
Cissé S, Eymard L, Ottlé C, Ndione JA, Gaye AT, Pinsard F. Rainfall Intra-Seasonal Variability and Vegetation Growth in the Ferlo Basin (Senegal). Remote Sensing. 2016; 8(1):66. https://doi.org/10.3390/rs8010066
Chicago/Turabian StyleCissé, Soukèye, Laurence Eymard, Catherine Ottlé, Jacques André Ndione, Amadou Thierno Gaye, and Françoise Pinsard. 2016. "Rainfall Intra-Seasonal Variability and Vegetation Growth in the Ferlo Basin (Senegal)" Remote Sensing 8, no. 1: 66. https://doi.org/10.3390/rs8010066
APA StyleCissé, S., Eymard, L., Ottlé, C., Ndione, J. A., Gaye, A. T., & Pinsard, F. (2016). Rainfall Intra-Seasonal Variability and Vegetation Growth in the Ferlo Basin (Senegal). Remote Sensing, 8(1), 66. https://doi.org/10.3390/rs8010066