A Point Cloud Filtering Approach to Generating DTMs for Steep Mountainous Areas and Adjacent Residential Areas

Abstract

Digital terrain models (DTMs) are considered important basic geographic data. They are widely used in the fields of cartography, land utilization, urban planning, communications, and remote sensing. Digital photogrammetry mainly based on stereo image matching is a frequently applied technique to generate DTMs. Generally, the process of ground filtering should be applied to the point cloud derived from image matching to separate terrain and off-terrain points before DTM generation. However, many of the existing filtering methods perform unsatisfactorily for steep mountainous areas, particularly when residential neighborhoods exist in the proximity of the test areas. In this study, an improved automated filtering method based on progressive TIN (triangulated irregular networks) densification (PTD) is proposed to generate DTMs for steep mountainous areas and adjacent residential areas. Our main improvement on the classic method is the acquisition of seed points with better distribution and reliability to enhance its adaptability to different types of terrain. A rule-based method for detecting ridge points is first applied. The detected points are used as additional seed points. Subsequently, a locally optimized seed point selection method based on confidence interval estimation theory is applied to remove the erroneous points. The experiments on two sets of stereo-matched point clouds indicate that the proposed method performs well for both residential and mountainous areas. The total accuracy values in the form of root-mean-square errors of the generated DTMs by the proposed method are 0.963 and 1.007 m; respectively; which are better than the 1.286 and 1.309 m achieved by the classic PTD method.

1. Introduction

1.1. Background

Since the digital terrain model (DTM) was introduced by Miller in 1958 [1], it has been widely adopted in a variety of scientific domains, including but not limited to cartography, land utilization, urban planning, communications, and remote sensing. In remote sensing, the importance of DTM is particularly emphasized because it is the basis for many applications, such as high-quality orthophoto acquisition [2], accurate ground object detection [3], and urban 3D reconstruction [4]. Currently, DTM data can be generated through several techniques, mainly including interferometric synthetic aperture radar (InSAR), airborne light detection and ranging (LiDAR), and digital photogrammetry based on aerial and satellite imagery.

InSAR is largely independent of weather conditions and can provide data even for heavily clouded areas; therefore, it has been successfully applied to generate global DTMs with coarse spatial resolution at worldwide scales [5,6,7]. LiDAR is known as an effective means of acquiring high-resolution elevation data. The DTMs established through this technique usually have an obvious advantage of high precision, especially for forested areas where measurements can be detected both on the ground surface and in the upper canopy. Digital photogrammetry is a relatively traditional method to generate DTMs at various scales. In this technique, a DTM is usually derived from stereo images with the use of automatic image-matching algorithms. The precision of a photogrammetric DTM is generally lower than those of DTMs established using the other two techniques because of the limitations of the matching algorithms. The vertical accuracy of a photogrammetric DTM may be even worse for dense forest areas, because a common optical sensor cannot capture images on the bare ground through the leaves. However, despite all its shortcomings, digital photogrammetry contributes to DTM generation in practical applications, considering the following reasons:

(1)

In large-scale applications, LiDAR provides an effective method for generating high-quality DTMs but at a relatively high cost, the investment of this technique could be limited [8]. In China, LiDAR is more often used in developed urban areas than in areas having little economic support. The surveying and mapping departments of less developed areas often prefer to use aerial photogrammetry in producing DTMs to cut on cost.

(2)

The performance of stereo image matching has been significantly developed in recent years. One of the representative algorithms is semi-global matching (SGM) [9]. SGM can generate a digital surface model (DSM) with a spatial resolution equivalent to that of stereo images; as a result, the density of the point cloud obtained from aerial digital photogrammetry could be close or even higher than that obtained from airborne LiDAR, allowing for the production of high-quality DTMs.

(3)

In a typical processing pipeline, after DTM generation, digital photogrammetry can continue to produce other mapping products, such as digital orthophoto maps and digital line graphics. Thus, this technique has a richer lineup of product types and a higher return on investment.

In large-scale data processing, whether in photogrammetry or LiDAR applications, ground filtering, which aims to automatically remove off-terrain points from the point cloud, is an essential step in DTM generation. In this paper, a research of ground filtering for point clouds derived from aerial stereo imagery is reported. The following subsection presents state-of-the-art methods in ground filtering. The performances of these methods are summarized.

1.2. Related Works

Ground filtering has been a well-researched topic for over 20 years. In the earlier literature, ground filtering was usually proposed as an auxiliary process along with image-matching and object-recognition algorithms and was implemented using some basic image-processing methods [10]. With the improvement of the spatial resolution of acquired DSM data, especially with the rise of LiDAR techniques, the complexity of ground-filtering in large-scale applications has started to draw attention. The problem has been gradually treated as an independent research topic. Current ground-filtering methods can be divided into four major groups according to their underlying concepts [11]: (1) slope-based; (2) morphology-based; (3) surface-based; and (4) segmentation-based filters. These algorithms are elucidated in the following subsections.

1.2.1. Slope-Based Filters

Slope-based filters assume that an obvious elevation discrepancy exists between a terrain point and an off-terrain point. Therefore, if the slope of two points is large, the point with a higher elevation can be considered an off-terrain point. One of the earliest slope-based filters was performed by checking the slope between two points [12]. On the basis of this pioneering, some improvements on the adaptability of undulating terrains [13] and automatic threshold determination [14] have been made. In other studies, the scan line information of LiDAR is used as auxiliary information for slope calculation to improve efficiency [15]. When dealing with unordered point clouds, some studies choose to partition the raw point cloud into a series of sequential isometric strips for slope calculation [16]. Similar methods have been successfully applied to rasterized point cloud data [17,18,19]. In these methods, slopes in multiple directions can be calculated easily and rapidly. The advantage of slope-based filter lies in its simple calculation and high efficiency. Nonetheless, the filtering results of these methods are always sensitive to slope threshold values, especially for complex terrains, such as mountainous areas.

1.2.2. Morphology-Based Filters

Morphology-based filters suggest that the real terrain should be close to a plane within a certain local area. In these methods, point cloud data are always first transformed into rasterized elevation images and then filtered using some existing image-processing algorithms. The progressive morphological filter is one of the early successful applications [20]. Subsequently, more improvements, such as multi-scale representation [21], image inpainting [22], Hermite transform [23], and top-hat transform [24,25], were proposed, some of which were demonstrated capable of obtaining high-accuracy filtering results. Morphology-based filters are generally applicable to relatively flat areas and have high efficiency. However, for considerably steep mountainous areas, these filters may not perform equally well when using the same parameters.

1.2.3. Surface-Based Filters

Surface-based filters are generally based on the principle that an actual terrain can be approximated with a continuous (or piecewise continuous) parametric surface. Thus, a point can be determined as either a terrain point or an off-terrain point by measuring its proximity to the surface. In some typical surface-based filtering approaches, a point is classified by comparing its elevation with its estimated values calculated by interpolation. Interpolation methods include linear prediction [26], thin-plate spline [24,27,28,29], quadratic surface fitting, and cubic spline model [30,31]. In other studies, a triangulated irregular network (TIN) is used to describe the terrain surface. The progressive TIN densification (PTD) proposed by Axelsson [32] is a classic TIN-based method. In this method, on the basis of an initial TIN constructed with the lowest points in local areas, the remaining points are iteratively added to the TIN surface by estimating the elevation difference from and angle to the closest triangle. In the experiments on 15 study samples with different types of terrain, PTD was proven to be the best method in terms of average overall accuracy [11,33]. Since the algorithm was integrated into the commercial software TerraScan [34], it has been extensively used in various applications. However, detecting discontinuous terrains, such as sharp ridges, remains difficult for PTD. Certain targeted processing should be performed to obtain better results. Furthermore, PTD is generally time consuming because of the numerous implementations of TIN construction for a sizable number of points. Integrating other algorithms, such as point cloud segmentation [35,36], with PTD, could obtain results better than those by the classic method.

1.2.4. Segmentation-Based Filters

These methods divide a point cloud into segments through certain processes before filtering. Some of these approaches are based on scan line segmentation [37,38]. Other approaches tend to segment the point cloud into surface clusters through region growing [39,40]. Afterward, the terrain segments are extracted based on a series of rules. For example, when a segment is above its neighborhood, all the points that belong to such a segment could probably be off-terrain points. In a flat area, the points that belong to a relatively larger segment can even be directly labeled as terrain points [41]. Segmentation-based filters can preserve the discontinuities in landscapes in some cases and can resist noise to a certain degree. However, the disadvantage of these methods is their dependence on good segmentation results. Point cloud segmentation can be a complex problem in numerous cases. Undulating terrains and rough surfaces can both pose challenges to segmentation-based filters.

1.2.5. Other Filtering Methods

Recently, the number of ground-filtering methods based on machine learning has been increasing. In these methods, the point cloud is generally labeled as different classes by supervised or unsupervised classification. Not only terrain points but also other objects, such as buildings and trees, are detected. Classifiers, including support vector machines [42], adaptive boosting (AdaBoost) [43,44], conditional random field [45,46], bootstrap aggregation [44], and random trees [47], are currently applied to ground point classification. The accuracy of AdaBoost method has been demonstrated to be close to that of the PTD method [44]. Methods based on machine learning represent a new research direction for ground filtering. However, reference training data are always required for these methods to achieve good results, and ensuring that the training dataset covers the characteristics of a sufficient number of terrain types is difficult.

1.3. The Proposed Approach

Although various terrains have been considered in the aforementioned methods, only few approaches to ground filtering for steep mountainous terrains have been reported. In the few studies focusing on mountainous terrains [19,27,30,31,48], residential areas are often not contained in the testing data. Given that these methods mainly aim to separate trees and relatively small objects on mountains, their performance on residential areas has not yet been confirmed.

In reality, having residential areas beside steep mountainous areas is common. However, most of the existing methods are often faced with a difficult situation when simultaneously dealing with these two types of terrain. For example, in the PTD method, seed points should generally be selected in a relatively large grid cell size to avoid detecting building points as terrains. Conversely, a small grid size is usually beneficial for filtering for mountainous areas.

In this study, an improved PTD method is proposed and applied to DTM generation for the point cloud derived from stereo aerial imagery. The point cloud data for the filtering experiments are obtained using the SGM algorithm [9]. The main feature of the proposed approach is the close proximity between the steep mountainous areas and the residential areas in the testing datasets. The purpose is to achieve good filtering results for the two types of terrain with equivalent parameters, so that the datasets can be processed without manual segmentation. Given that the initial seed points can hardly be selected from the ridge of the mountain, a rule-based method is first proposed to detect potential ridge points. An optimal selection method based on confidence interval estimation theory is then applied to eliminate the erroneous points among the seed points. The memory-efficient TIN densification strategy proposed in our previous work [49] is adopted to improve the processing efficiency for point clouds with high density. The experiments on the two datasets demonstrate that the proposed method can achieve relatively high accuracy for both residential and mountainous areas. In comparative trials, the root-mean-square errors (RMSEs) of the DTMs generated by our method are proven to be lower than those achieved by the classic PTD method.

The remainder of this article is organized as follows. Section 2 describes the proposed filtering method. The employed testing data, the experimental and evaluation results are reported in Section 3. The discussion of the results is presented in Section 4. Conclusions are given in Section 5.

2. Methodology

The proposed approach is based on the classic PTD algorithm. In-depth explanations on the principle of PTD have been provided in the literature [32,35,36]; thus, explaining the PTD principle in this paper is no longer necessary. The following processes are used to improve the performance of the algorithm: (1) the potential ridge point detection from the TIN constructed with sparse seed points; (2) the optimal selection of seed points based on confidence interval estimation theory; and (3) a memory-efficient TIN densification strategy for point clouds with high density. Each process is further described below.

2.1. Potential Ridge Point Detection

In the classic PTD algorithm, the parameter of grid cell size $w$, for seed point selection has a significant effect on the filtering results. As shown in Figure 1, $w$ should typically be set larger than the maximum building size to avoid selecting seed points on the roof of buildings. However, given that the lowest point in the grid is selected as the seed point, the selected seed points hardly appear in the vicinity of the mountain ridge. Thus, completely preserving the real terrain at the ridge could be difficult during the subsequent TIN densification process. If some points near the ridge could be detected and used as additional seed points, the filtering results for mountainous areas will be improved.

Figure 1. Seed point selection for a steep mountainous area with buildings nearby. The real terrain and the corresponding point cloud are separately drawn in two parts. In part (a), the buildings, trees, and topography are indicated with different colors; In part (b), the cyan dashed line defines the grid cell for seed point selection; the small red diamond shape represents the lowest point selected as seed point in each grid, and the brown dashed line represents the initial terrain constructed with the seed points.

Figure 1. Seed point selection for a steep mountainous area with buildings nearby. The real terrain and the corresponding point cloud are separately drawn in two parts. In part (a), the buildings, trees, and topography are indicated with different colors; In part (b), the cyan dashed line defines the grid cell for seed point selection; the small red diamond shape represents the lowest point selected as seed point in each grid, and the brown dashed line represents the initial terrain constructed with the seed points.

On the basis of the sparse TIN structure constructed with the initial seed points, a rule-based ridge point detection method is designed. The main idea of this method is to detect the triangles that are likely to be located on the ridge. Within a certain range around the gravity center of the triangle, the lowest point is selected as an additional seed point. In our approach, this type of triangle is referred to as the “ridge triangle”, which can be determined according to the following assumptions:

(1)

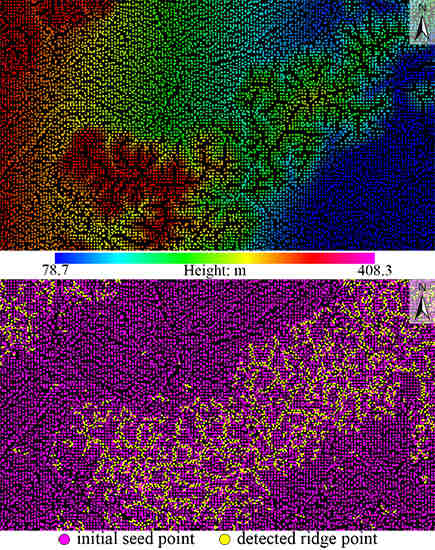
The descending trend on the opposite sides of the ridge. Owing to this feature, Figure 1b shows that the distance between the seed points at the ridge is apparently longer. Compared with others, the horizontal component $\Delta l$ of this distance could be closer to 2$w$. Thus, the $\Delta l$ values for the three sides of the judging triangle in the TIN are calculated. If at least one $\Delta l$ is greater than the threshold $l_r$, the triangle can be inferred as a potential ridge triangle. In our approach, $l_r$ is the product of the coefficient $m_r$ and $w$, with $m_r$ generally having a value close to 2. Considering that the topographical trend of the ridge can be represented along the X-axis or Y-axis direction, $\Delta l$ can be calculated using the following equation:

$$\Delta l=\max \{\left|X_1-X_2\right|,\left|Y_1-Y_2\right|\}$$

(1)

where $X_i$ and $Y_i$ are the space coordinates of the triangle vertices.

(2)

The convex slope inversion constraint. The main implication of this assumption is that the slope changes dramatically at the ridge, as proposed in the earlier literature for ridge point extraction from a DTM [50]. In the TIN structure constructed with sparse seed points, the changing trend of the slope is retained even if the topographic feature of the ridge has weakened. According to this trend, the potential ridge triangle can be extracted from the TIN by calculating the dihedral angle between the judging triangle and its adjacent triangles. The triangles that constitute a considerable angle with the ridge triangle should exist on both sides of the mountain. In our approach, the triangles connected to the directly adjacent triangles are also used for the judgment considering that these three triangles may only include triangles on one side, as shown in Figure 2. A triangle is generally determined as a ridge triangle if at least two triangles in its vicinity fulfill the following conditions: (i) the dihedral angle between the judging triangle and the adjacent triangle is greater than the threshold ${\theta }_r$; (ii) the gravity center of the adjacent triangle is located below the plane of the judging triangle; and (iii) no common point exists between the satisfied triangles.

Figure 2. Adjacent triangles for determining the ridge triangle. The green triangle represents the judging triangle, the dark blue triangles represent the triangles directly adjacent to the judging triangle, and the light blue triangles represent the triangles connected to the directly adjacent triangles.

Figure 2. Adjacent triangles for determining the ridge triangle. The green triangle represents the judging triangle, the dark blue triangles represent the triangles directly adjacent to the judging triangle, and the light blue triangles represent the triangles connected to the directly adjacent triangles.

In summary, when a triangle in the sparse TIN satisfies Assumptions (1) and (2), it can be detected as a ridge triangle. In general, the terrain is usually not flat at the ridge, which means that large artificial objects rarely exist therein. Therefore, in our approach, the lowest point within a radius of 2 m from the gravity center of the triangle is selected as the ridge point. Figure 3 shows the results of the ridge point detection for one of the experimental datasets in our approach. Figure 3a,b illustrate obvious gaps along the ridge line; these gaps are clearly caused by the descending trend of the ridge terrain. Figure 3c,d show that, in most of the gaps, the potential ridge points can be detected by the proposed method. Figure 3e,f indicate that the terrain surface constructed with the initial seed points and the ridge points preserves the topographic features more precisely.

Figure 3. Results of ridge point detection. (a) Initial seed points selected from the stereo-matched point cloud that are colored according to their elevations; (b) Enlarged view of the rectangular area in (a); (c) Ridge points detected based on the initial seed points; (d) Enlarged view of the rectangular area in (c); (e,f) Vertical views of the TIN surfaces constructed using the points in (b,d), respectively.

Figure 3. Results of ridge point detection. (a) Initial seed points selected from the stereo-matched point cloud that are colored according to their elevations; (b) Enlarged view of the rectangular area in (a); (c) Ridge points detected based on the initial seed points; (d) Enlarged view of the rectangular area in (c); (e,f) Vertical views of the TIN surfaces constructed using the points in (b,d), respectively.

2.2. Optimal Selection of Seed Points

Erroneous points are inevitably included in the potential ridge points. For example, in the lower right area of Figure 3c, a few ridge points may be erroneously detected. Meanwhile, in the application of the PTD algorithm for steep mountainous terrains, one of the essential requisites to achieve good results is to set a relatively small $w$. When $w$ drops to a certain size, errors would appear among the initial seed points in residential areas. Thus, an optimal selection method of seed points based on confidence interval estimation theory is proposed in our approach to eliminate the errors from the initial seed points and the ridge points.

A small range of topographic surface can generally be well fitted using a conicoid model. When the model is estimated by seed points within a local area, while treating the point elevations as observations, gross errors can be detected according to their residuals.

According to confidence interval estimation theory, the confidence intervals corresponding to residuals can be estimated to detect gross errors by judging whether the residual falls within the corresponding confidence interval. The details are as follows.

In a local conicoid model, local seed points satisfy the following equation:

$$Y=X\beta +\epsilon$$

(2)

where $Y$ is the elevation vector of the points, $\beta$ is the unsolved parameter vector, and $X$ is the corresponding coefficient matrix constructed by the corresponding plane coordinates, as shown by Equation (3):

$$X=\left[\begin{array}{cccccc}1& x_1& y_1& x_1^2& x_1{y}_1& y_1^2\\ 1& x_2& y_2& x_2^2& x_2{y}_2& y_2^2\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 1& x_n& y_n& x_n^2& x_n{y}_n& y_n^2\end{array}\right]$$

(3)

where $n$ is the number of seed points and $x_i$ and $y_i$ are the plane coordinates of the $i$-th seed point ($i=1,2,\cdots ,n$).

In Equation (2), $\epsilon$ obeys the following multivariate normal distribution:

$$\epsilon ~N(0,\Sigma )$$

(4)

where $\Sigma ={\sigma }_0^2{P}^{-1}$ and $P$ is the weight matrix, which is an identity matrix in our approach.

According to the least square method, the parameter vector can be estimated as follows:

$$\widehat{\beta }={(X^{T}PX)}^{-1}{X}^{T}PY$$

(5)

Furthermore, in confidence interval estimation, normalized residuals should be solved using a covariance matrix, which can be estimated by the following equation:

$$Q_{\widehat{V}\widehat{V}}=P^{-1}-X{(X^{T}PX)}^{-1}{X}^T$$

(6)

The residual for every seed point can be obtained as follows:

$${\widehat{v}}_i=X_i\widehat{\beta }-Y_i$$

(7)

where ${\widehat{v}}_i$ is the estimated residual for the $i$-th point and $Y_i$ is the corresponding observed elevation.

The normalized residuals can be considered statistics that obey the following $t$ distribution:

$$t_i=\frac{{\widehat{v}}_i}{{\widehat{\sigma }}_0\sqrt{q_{ii}}}\sim t_{n-u-1}$$

(8)

where $q_{ii}$ is the $i$-th element of the diagonal of $Q_{\widehat{V}\widehat{V}}$ and ${\widehat{\sigma }}_0$ is the unit weighted RMSE calculated by the following expression:

$${\widehat{\sigma }}_0=\sqrt{\frac{{{\displaystyle \sum }}_{i=0}^n{\widehat{v}}_i^2}{n-u-1}}$$

(9)

where $n$ is the number of observations and $u$ is the parameter number of Equation (2).

Given a confidence level of $1-\mathsf{\alpha }$ (confidence probability), the corresponding confidence intervals $(\underset{¯}{t},\overline{t})$ of the normalized residuals can be estimated according to the $t$ distribution. In other words, the statistic $t_i$ should satisfy the following inequation:

$$\underset{¯}{t}<t_i<\overline{t}$$

(10)

Thus, if $t_i$ does not fall in the confidence interval, then the corresponding point can be considered a gross error.

The seed points can be judged one by one on the basis of the preceding analysis. Every time a point is judged, the neighboring points are gathered. If the residual of the judging point cannot pass the significance test, the point is eliminated. Using the TIN structure, the neighboring points can be determined by an iterative method [51]: all the points adjacently connected to the judging point are first collected; more points that are adjacently connected to the collected points are then identified and gathered continually. In our approach, the recommended iteration number is 2.

A major effect of the optimized selection for seed points is that the grid cell size $w$ can be assigned to a larger range. According to the authors’ experience, $w$ can generally be set to half of the value adopted in the classic PTD algorithm. Figure 4 shows the optimal selected results of the seed points. After optimization, the gross errors among the initial seed points and the ridge points are both well eliminated, whereas most of the additional ridge points are preserved.

Figure 4. Triangulated irregular network (TIN) surfaces constructed with seed points before and after optimal selection. (a) Results of the initial seed points; (b) Results of the seed points after adding the detected ridge points; (c) Results of the seed points after optimal selection. The yellow ellipses indicate the areas where gross errors among the initial seed points appear, and the black ellipses indicate the areas where gross errors among additional ridge points appear.

Figure 4. Triangulated irregular network (TIN) surfaces constructed with seed points before and after optimal selection. (a) Results of the initial seed points; (b) Results of the seed points after adding the detected ridge points; (c) Results of the seed points after optimal selection. The yellow ellipses indicate the areas where gross errors among the initial seed points appear, and the black ellipses indicate the areas where gross errors among additional ridge points appear.

2.3. A Memory-Efficient TIN Densification Strategy

During the filtering process for the point clouds with high density, computational efficiency and memory consumption are significant problems in the implementation of the PTD algorithm. In our approach, the matching result obtained by SGM can be a point cloud with very high density. Considering that TIN construction requires significant memory, sufficient memory to process excessive points may be difficult to achieve. In practical applications, a point cloud with a large number of points is often divided into square tiles or subsampled into a lower density before filtering. However, partitioning the data may result in the “border effect” [30], and some topographic details may be lost because of subsampling, causing missed detection of terrain points in certain situations. For example, the original point data (in Figure 5a) are subsampled by keeping the lowest point in the grid cell (in Figure 5b). If the threshold of the maximum distance for TIN densification is valued between $d_A$ and $d_B$, then terrain point $P_A$ will not be detected.

Figure 5. Example of TIN densification in a local area. The brown line represents the actual terrain, and the blue dashed line represents the TIN surface constructed with the detected terrain points. The red diamond shapes represent the points labeled as terrain points, and the white diamonds represent the points labeled as off-terrain points. (a) Sectional view of the original point cloud, where $d_A$ and $d_B$ are the distances from $P_A$ and $P_B$ to the corresponding triangle, respectively, and $m$ is the grid cell size for determining the lowest point; (b) $P_A$ cannot be labeled as a terrain point if the points are subsampled in advance; (c,d) Densification results using the proposed strategy in two iterations, where $P_A$ is successfully labeled.

Figure 5. Example of TIN densification in a local area. The brown line represents the actual terrain, and the blue dashed line represents the TIN surface constructed with the detected terrain points. The red diamond shapes represent the points labeled as terrain points, and the white diamonds represent the points labeled as off-terrain points. (a) Sectional view of the original point cloud, where $d_A$ and $d_B$ are the distances from $P_A$ and $P_B$ to the corresponding triangle, respectively, and $m$ is the grid cell size for determining the lowest point; (b) $P_A$ cannot be labeled as a terrain point if the points are subsampled in advance; (c,d) Densification results using the proposed strategy in two iterations, where $P_A$ is successfully labeled.

A memory-efficient TIN densification strategy for high-density point clouds is adopted to address the aforementioned problems. This strategy was proposed in our previous work [49] and can be summarized in the following steps:

(1)

The optimized seed points are all labeled as terrain points.

(2)

A TIN is constructed using terrain points.

(3)

All the off-terrain points are judged one by one. The distance and angles are calculated for the judging point and its corresponding triangle. The point is then labeled as a terrain point if the threshold condition is satisfied. After traversing all the off-terrain points, the total number of current terrain points, $N_{ground}^i$ is recorded, where $i$ represents the iteration rounds.

(4)

A grid with cell size $m$ is created, and all grid cells are then traversed. If a grid cell has terrain points in it, then only the lowest terrain point is retained, whereas all the other terrain points are relabeled as off-terrain points. The value of $m$ can be determined according to the resolution of the final acquired DTM.

(5)

Steps (2) to (4) are repeated. In step (3), the proportion of the increased terrain points in the total points is calculated as follows:

$$p=(N_{ground}^i-N_{ground}^{i-1})/N_{total}$$

(11)

When $p$ is larger than the threshold $p_{min}$ the following step is performed; otherwise, the loop ends. In our approach, $p_{min}$ is set to 0.001.

Through this strategy, instead of subsampling the point cloud before filtering, the points presenting a more detailed topography are preserved. Therefore, the rejection of terrain points can be avoided in some situations when using the same parameters. As shown in Figure 5c,d, $P_A$ can be successfully labeled as a terrain point in our approach using the same distance threshold between $d_A$ and $d_B$.

In this strategy, only the lowest points in the grid cells are used to construct a TIN during the densification process. Thus, the number of points for TIN construction is controlled, and the memory consumption is reduced. Specifically, the theoretical maximum number of points for TIN construction can be limited to:

$$N_{max}=W·H/m^2$$

(12)

where $W$ and $H$ represent the width and height of the bounding rectangle of the point cloud data, respectively; $m$ is the grid cell size aforementioned.

3. Experiments and Results

3.1. Testing Data

The testing data used in the experiments are obtained from Shaoguan, a southern city in the Guangdong Province of China. The main terrain in Shaoguan is mountainous, but many residential areas also exist in the city. The aerial images are captured using a Digital Mapping Camera with a focal length of 92 mm at 3600 m altitude. The forward overlap of images is 65%, and the size of each image is 14,144 × 15,552 pixels with a spatial resolution of 0.2 m.

Two sets of point clouds matched from two consecutive stereo image pairs are used for the experiments. The maximum elevation differences in the two datasets are more than 300 m. Each of the point cloud dataset covers an area of approximately 3100 × 1800 m². The target of this study is to generate DTMs with grid size of 1 m; thus, in order to avoid processing excessively redundant data, the matching results are subsampled into one-half of the original resolution. The point density of the subsampled point cloud is 6 points/m², and the total number of points for each dataset is over 12 million.

In the datasets, eight sites are selected to evaluate the filtering results, including four residential sites and four mountainous sites. Figure 6 shows the experimental and evaluation areas in the coordinate system of the 1984 World Geodetic System. Given that the ground truth data are unavailable in the testing area, TerraScan software is adopted to classify the points of each site into terrain and off-terrain points by careful manual editing. The obtained ground points are interpolated into a regular-grid DTM, which is then used as a reference DTM.

Figure 6. Experimental and evaluation areas. (a,b) TIN surfaces constructed with the point clouds of the two datasets, which are colored based on the texture of the aerial images. The red rectangles indicate the areas for DTM accuracy evaluation of the residential areas, and the yellow rectangles indicate the areas for evaluating mountainous areas.

Figure 6. Experimental and evaluation areas. (a,b) TIN surfaces constructed with the point clouds of the two datasets, which are colored based on the texture of the aerial images. The red rectangles indicate the areas for DTM accuracy evaluation of the residential areas, and the yellow rectangles indicate the areas for evaluating mountainous areas.

3.2. Evaluation and Comparison

The proposed algorithms are implemented using C++ language. In seed point optimization, the confidence interval must be obtained from the t distribution table according to the confidence probability. This process is automatically accomplished using the GNU Scientific Library [52]. A desktop computer with a 64-bit Windows 7 operating system, a quad-core Intel Core i5-3470 CPU, 3.2 GHz, and 4 GB memory is utilized for the experiments. Given that the proposed approach is an improved PTD method, the implementation of the classic PTD method in the TerraScan software package is used for comparison. Meanwhile, three other filtering algorithms including progressive morphology (PM) [20], multiscale curvature (MC) [27] and linear prediction (LP) [26] are also tested in our experiment. These three methods are implemented in the free softwares of ALDPAT [53], MCC-LIDAR [54] and FUSION [55], respectively.

Table 1 shows the main parameters used by the proposed filtering method. The first five parameters are shared by the classic PTD algorithm and the proposed algorithm and are set to the same values across the experiments. The detailed meanings of these parameters are given in [35]. The last three parameters are the additional parameters in our approach. Parameters for the proposed method and all the compared methods are tuned for maximum performance. However, it should be noted that the datasets with two types of terrains are processed with equivalent parameters. The most important criterion for parameter selection is to balance the filtering results between the residential and mountainous areas.

Table 1. Main parameters of the proposed method.

Parameters	Values
Grid cell size $w$	20 m
Maximum terrain angle $t$	88.0°
Maximum angle $\theta$	6.0°
Maximum distance $d$	1.4 m
Minimum edge length $l$	1 m
Minimum times of edge length in ridge $m_r$	1.5
Minimum angle in ridge ${\theta }_r$	25
Confidence probability $1-\alpha$	98%

Table 1. Main parameters of the proposed method.

Parameters	Values
Grid cell size $w$	20 m
Maximum terrain angle $t$	88.0°
Maximum angle $\theta$	6.0°
Maximum distance $d$	1.4 m
Minimum edge length $l$	1 m
Minimum times of edge length in ridge $m_r$	1.5
Minimum angle in ridge ${\theta }_r$	25
Confidence probability $1-\alpha$	98%

Given that this study aims to generate high-quality DTM data, the ground points obtained by filtering algorithms are interpolated into DTMs for evaluation. The elevation discrepancies between the generated and the reference DTMs are computed, and the RMSEs calculated from these discrepancies are used to quantify the accuracy of the generated DTM [56]. Apart from the calculation of $RMSE$ for every single site, the overall accuracy values for all residential and mountainous sites respectively represented by $RMS{E}_r$ and $RMS{E}_m$ are calculated for each dataset. The total accuracy $RMS{E}_{total}$ for each dataset is also calculated based on the statistics of points for all the sites.

Table 2 and Table 3 list the RMSE values for the eight sites in the two datasets, where $RMS{E}_i$ represents the $RMSE$ value for Site i. For residential areas, the DTM of the proposed method achieved the highest accuracy value among the five compared methods. For mountainous areas, MC and LP generated the best results in Dataset 1 and 2, respectively, with the proposed method following by a slight difference. For total areas, the proposed method is obviously better than the other methods. Therefore, when using the same set of parameters for filtering, the proposed method can achieve relatively high accuracy values for both residential and mountainous areas.

Table 2. Comparison of the RMSE results (in meters) for Dataset 1.

Method	$RMS{E}_1$	$RMS{E}_2$	$RMS{E}_r$	$RMS{E}_3$	$RMS{E}_4$	$RMS{E}_m$	$RMS{E}_{total}$
PM	1.022	1.381	1.266	1.652	1.085	1.423	1.353
MC	0.860	1.296	1.161	1.309	0.965	1.165	1.163
LP	1.431	1.638	1.568	1.348	1.066	1.228	1.395
PTD	0.440	0.742	0.651	1.750	1.509	1.645	1.286
Proposed	0.455	0.359	0.396	1.461	0.960	1.259	0.963

Table 2. Comparison of the RMSE results (in meters) for Dataset 1.

Method	$RMS{E}_1$	$RMS{E}_2$	$RMS{E}_r$	$RMS{E}_3$	$RMS{E}_4$	$RMS{E}_m$	$RMS{E}_{total}$
PM	1.022	1.381	1.266	1.652	1.085	1.423	1.353
MC	0.860	1.296	1.161	1.309	0.965	1.165	1.163
LP	1.431	1.638	1.568	1.348	1.066	1.228	1.395
PTD	0.440	0.742	0.651	1.750	1.509	1.645	1.286
Proposed	0.455	0.359	0.396	1.461	0.960	1.259	0.963

Table 3. Comparison of the RMSE results (in meters) for Dataset 2.

Method	$RMS{E}_5$	$RMS{E}_6$	$RMS{E}_r$	$RMS{E}_7$	$RMS{E}_8$	$RMS{E}_m$	$RMS{E}_{total}$
PM	1.340	1.690	1.486	1.445	2.032	1.709	1.612
MC	1.296	1.633	1.437	1.349	1.090	1.250	1.338
LP	1.761	2.044	1.876	1.298	1.047	1.202	1.544
PTD	0.552	0.904	0.710	1.601	1.715	1.649	1.309
Proposed	0.591	0.603	0.596	1.271	1.215	1.249	1.007

Table 3. Comparison of the RMSE results (in meters) for Dataset 2.

Method	$RMS{E}_5$	$RMS{E}_6$	$RMS{E}_r$	$RMS{E}_7$	$RMS{E}_8$	$RMS{E}_m$	$RMS{E}_{total}$
PM	1.340	1.690	1.486	1.445	2.032	1.709	1.612
MC	1.296	1.633	1.437	1.349	1.090	1.250	1.338
LP	1.761	2.044	1.876	1.298	1.047	1.202	1.544
PTD	0.552	0.904	0.710	1.601	1.715	1.649	1.309
Proposed	0.591	0.603	0.596	1.271	1.215	1.249	1.007

Among the filtering results, we select a mountain site and a residential site from the two datasets to perform a visual evaluation. The selected sites include Sites 1, 4, 6, and 7. Figure 7, Figure 8, Figure 9 and Figure 10 show the comparative results of the generated DTMs for these sites. Figure 7 and Figure 9 indicate that the problems of PM, MC and LP lie in the acceptance of obvious objects as terrains. Figure 8 and Figure 10 indicate that more points near the mountain ridge are rejected by PM and PTD. The proposed method achieves a better overall performance on the two different types of terrain.

Figure 7. TIN surfaces constructed with the points of Site 1 and its filtering results. (a) Original stereo-matched point cloud; (b) Reference DTM obtained from manual editing; (c–g) Filtering results of PM, MC, LP, PTD and the proposed method, respectively.

Figure 7. TIN surfaces constructed with the points of Site 1 and its filtering results. (a) Original stereo-matched point cloud; (b) Reference DTM obtained from manual editing; (c–g) Filtering results of PM, MC, LP, PTD and the proposed method, respectively.

Figure 8. Orthographs of TIN surfaces of Site 4 and its filtering results. (a) Original stereo-matched point cloud; (b) Reference DTM obtained from manual editing; (c–g) Filtering results of PM, MC, LP, PTD and the proposed method, respectively. The white ellipses indicate the areas where the terrain points near the ridge are obviously rejected during the filtering process.

Figure 8. Orthographs of TIN surfaces of Site 4 and its filtering results. (a) Original stereo-matched point cloud; (b) Reference DTM obtained from manual editing; (c–g) Filtering results of PM, MC, LP, PTD and the proposed method, respectively. The white ellipses indicate the areas where the terrain points near the ridge are obviously rejected during the filtering process.

Figure 9. TIN surfaces constructed with the points of Site 6 and its filtering results. (a) Original stereo-matched point cloud; (b) Reference DTM obtained from manual editing; (c–g) Filtering results of PM, MC, LP, PTD and the proposed method, respectively.

Figure 9. TIN surfaces constructed with the points of Site 6 and its filtering results. (a) Original stereo-matched point cloud; (b) Reference DTM obtained from manual editing; (c–g) Filtering results of PM, MC, LP, PTD and the proposed method, respectively.

Figure 10. Orthographs of TIN surfaces of Site 7 and its filtering results. (a) Original stereo-matched point cloud; (b) Reference DTM obtained from manual editing; (c–g) Filtering results of PM, MC, LP, PTD and the proposed method, respectively. The white ellipses indicate the areas where the terrain points near the ridge are obviously rejected during the filtering process.

Figure 10. Orthographs of TIN surfaces of Site 7 and its filtering results. (a) Original stereo-matched point cloud; (b) Reference DTM obtained from manual editing; (c–g) Filtering results of PM, MC, LP, PTD and the proposed method, respectively. The white ellipses indicate the areas where the terrain points near the ridge are obviously rejected during the filtering process.

The processing times of PM, MC, LP, PTD and the proposed method are 198, 600, 43, 110 and 111 s for Dataset 1 and 205, 660, 47, 103 and 115 s for Dataset 2, respectively. It can be seen that the speed of the proposed method is very close to that of the classic PTD. The efficiency of the proposed approach should be acceptable for most general applications.

4. Discussion

4.1. Main Features of the Proposed Method

Some improvements on the classic PTD algorithm are proposed in this study. The improved method is successfully applied to DTM generation using the point cloud derived from stereo aerial images. The main advantage of the proposed approach is the generation of relatively good filtering results for both residential areas and mountainous terrains with the use of the same set of parameters.

Many of other filtering methods use different parameters when dealing with different terrains [18,29,35,36]. Some experiments confirm that better results can be obtained with optimized parameters than single parameters [22]. It means that in such methods, when the data include both residential and mountainous areas, the two different terrains are preferably to be segmented to obtain better filtering results. However, this process usually requires manual intervention and can be time consuming. By contrast, the proposed method can achieve good results without data segmentation, thereby considerably improving the applicability and automation degree of the PTD algorithm.

Most of the previous works have adopted the LiDAR data provided by the International Society for Photogrammetry and Remote Sensing (ISPRS) for evaluation and comparison [11]. This study focuses more on validating the feasibility of generating DTM with stereo-matched point cloud; hence, the ISPRS benchmark datasets are not used in our approach. The other feature of our approach is the high-density and steep slope of the processed point cloud data. The maximum height difference in our experimental datasets is more than 300 m. In addition, there are some filtering methods particularly developed for mountainous terrains [19,27,30,31,48]; however, compared with our method, the practicability of these methods for residential areas has not been demonstrated.

4.2. Sensitivity Analysis of the Parameters

Among the eight main parameters defined in the proposed method, the first five parameters are shared with the classic PTD algorithm. Since TerraScan has been able to give the recommended values for these parameters that perform well in many applications, this study determines these parameters by fine tuning the values suggested from TerraScan. $m_r$, ${\theta }_r$, and $\mathsf{\alpha }$ are three new parameters in our approach. These three parameters are determined according to their influence on the filtering results. Both $m_r$ and ${\theta }_r$ are used for ridge point detection. The influence of these two parameters can be generally concluded as follows: when $m_r$ and ${\theta }_r$ decrease, the detected ridge points in mountainous areas increase, but $RMS{E}_r$ or even $RMS{E}_{total}$ also increases. The reason is that the gradually increasing gross errors among the detected ridge points cannot be satisfactorily eliminated in the subsequent optimization process. Parameter $\mathsf{\alpha }$ is used for the optimal selection of seed points; when this parameter increases from 0, $RMS{E}_r$ decreases. However, when $\mathsf{\alpha }$ increases to a certain value (larger than 0.05 in our approach), the DTM accuracy for mountainous areas is significantly affected, because some local areas of the mountainous terrains cannot be precisely approximated with a conicoid model. The ridge points or even the initial seed points in these areas may be erroneously removed. A significantly large $\mathsf{\alpha }$ not only increases $RMS{E}_m$, but also adversely affects results for residential areas because only a few seed points can be retained after optimization.

Among the five parameters of the classic PTD algorithm, the grid cell size, $w$, is the parameter with an obvious effect on the final results. Multiple $w$ values ranging from 10 m to 55 m are used to generate the filtering results of the two methods for Dataset 1 to investigate the influence of the grid cell size on the classic PTD and the proposed method. As shown in Figure 11, for residential areas, the DTM accuracy of PTD is apparently improved from 10 m to 35 m and becomes stable when $w$ is greater than 35 m, whereas the accuracy of the proposed method is generally stable, except when $w$ is 10 m. For mountainous areas, the accuracies of both methods are reduced with increasing $w$, but the proposed method is less sensitive. Both methods achieve the highest accuracies when $w$ is equal to 15 m because the buildings in Dataset 1 are generally small.

Figure 11. DTM accuracy values obtained by PTD and the proposed method using different $w$ values. (a–c) Comparative results of $RMS{E}_r$, $RMS{E}_m$ and$RMS{E}_{total}$ respectively.

Figure 11. DTM accuracy values obtained by PTD and the proposed method using different $w$ values. (a–c) Comparative results of $RMS{E}_r$, $RMS{E}_m$ and$RMS{E}_{total}$ respectively.

4.3. Accuracies, Errors, and Uncertainties

Given that the ground truth data are unavailable, the manual filtering results are used as the reference data in our approach. The comparative trials suggest that the DTM accuracy obtained by the proposed method is better than those of the comparative methods when residential and mountainous areas are contained in a single dataset.

In order to conduct further analysis on the filtering accuracies of the testing methods, three kinds of errors defined in [11], namely, type I errors (i.e., omission errors), type II errors (i.e., commission errors) and total errors are evaluated. The evaluation results in Figure 12 suggest that, for residential areas (Site 1, 2, 5 and 6), most of the testing methods have relatively low type I errors in our experiment. MC has the lowest type I errors for all the four sites, the type I errors of the proposed method rank 2nd at Site 1 and 5, and rank 4th and 3rd at Site 2 and 6, respectively. In the assessment of type II errors, PTD and the proposed method perform better than other methods, PTD ranks 1st at Site 1, 2 and 5, the proposed method ranks 1st at Site 6. Meanwhile, the two methods also have lower total errors than other methods. PTD ranks 1st at Site 1 and 2, the proposed method ranks 1st at Site 5 and 6. For mountainous areas (Site 3, 4, 7 and 8), the proposed method has the lowest type I errors for all the sites, but it also has the highest type II errors for all the sites in the meantime. In the assessment of total errors, the proposed method can be considered as the best method, which ranks 3rd at Site 3, and ranks 1st at Site 4, 7 and 8, respectively. The second best method for mountainous area is MC, which ranks 2nd at all the four sites. It can be seen that the proposed method performs worse in the assessment of type II errors than that of type I errors. However, considering that in the manual editing process, the cost of repairing the type II errors is significantly lower than that of repairing the type I errors [11], the proposed method should require less human intervention compared to the other filters.

Considering that the point cloud data processed are obtained from stereo image matching, the errors of image matching directly influence the quality of the final DTM. The dense matching for stereo images is a complex issue. The matching result can be influenced by many factors, such as the precision of aerial triangulation adjustment, the lack of image texture, and the uneven brightness. However, the point cloud in our approach is generated by SGM, which has been demonstrated to be a stable algorithm on the practical processing of aerial image matching [9].

When steep terrain is coupled with a forest cover, defining a DTM becomes difficult because points on low branches may be mistaken as terrains. The proposed method tries to prevent detecting vegetation points as terrains in two ways. First, if there are vegetation points with obvious higher elevation that are wrongly selected as the ridge points, they are likely to be removed as gross errors in the subsequent optimization process. Moreover, the adopted TIN densification strategy can resist the disturbance of vegetation points to a certain extent, because only the lowest points in the grid cells are used for TIN construction during the densification process.

Figure 12. Three types of errors of the comparative filtering methods for the eight testing sites. (a–c) Type I errors, type II errors and total errors of the comparative methods for the testing sites, respectively.

Figure 12. Three types of errors of the comparative filtering methods for the eight testing sites. (a–c) Type I errors, type II errors and total errors of the comparative methods for the testing sites, respectively.

Considering that the point cloud data processed are obtained from stereo image matching, the errors of image matching directly influence the quality of the final DTM. The dense matching for stereo images is a complex issue. The matching result can be influenced by many factors, such as the precision of aerial triangulation adjustment, the lack of image texture, and the uneven brightness. However, the point cloud in our approach is generated by SGM, which has been demonstrated to be a stable algorithm on the practical processing of aerial image matching [9].

Unlike airborne LiDAR data, the point cloud obtained from aerial photogrammetry can only define the upper canopy surface in forest areas with dense leaves, causing considerable uncertainty about the absolute accuracy of the generated DTM. However, the main topographic features are retained in the stereo-matched point cloud. Although the accuracy is affected by labeling some leaf points as terrain points, the obtained DTM remains useful for many practical applications, such as image rectification, floodplain mapping, and land erosion analysis.

Currently, the improvement of the proposed method is verified using point cloud data derived from stereo images at only one location, thus the filtering results might vary for other different scenarios. The proposed method is mainly designed for DTM generation with high resolution (1 m), the experimental results show that it performs well for stereo-matched point cloud with 6 points/m² density. However, in-depth experiments and analyses for LiDAR data have not been done in our works. Considering that compared with stereo-matched point cloud, LiDAR data may have lower density and represent a more complex spatial distribution, it should be pointed out that the applicability of the proposed method for LiDAR data remains uncertain.

5. Conclusions

An improved progressive TIN (triangulated irregular networks) densification (PTD) algorithm is proposed for digital terrain model (DTM) generation with the point clouds derived from aerial image matching. Given that residential and mountainous areas are contained in a single dataset, this approach aims to achieve relatively high accuracy values for the two different terrains using the same set of parameters. The main improvements are as follows: first, a rule-based method for detecting ridge points is used to enhance filtering performance for steep mountainous terrains. The detected potential ridge points are used as additional seed points. Second, an optimal selection method based on confidence interval estimation theory is applied to seed points to eliminate the erroneous points among the potential ridge points and the initial seed points. A memory-efficient TIN densification strategy is also proposed to process high-density point clouds. In this strategy, the number of points for TIN construction is controlled, and some points presenting a detailed topography can be preserved.

The experiments on two sets of stereo-matched point clouds with more than 12 million points indicate that the proposed method performs well both for mountainous and residential areas. The total accuracy values of the generated DTMs in the form of root-mean-square errors are 0.963 and 1.007 m, respectively, which are better than the 1.286 and 1.309 m achieved by the classic PTD method. The times consumed by the proposed method for the two datasets are 111 and 115 s, respectively, which are very close to those of the classic PTD method and can thus meet the requirements of most applications.

However, the proposed approach mainly focuses on the overall accuracy for different types of terrain and in the process fails to provide an in-depth analysis of the filtering results for local areas. A subsequent study will investigate the problems encountered in detail, and the applicability of our method to point clouds obtained from airborne light detection and ranging will also be considered in the future.