Using a Kalman Filter to Assimilate TRMM-Based Real-Time Satellite Precipitation Estimates over Jinghe Basin, China

Abstract

In this study, efforts are focused on the comparison and validation of standard Tropical Rainfall Measuring Mission (TRMM) Multisatellite Precipitation Analysis (TMPA) products—Version-7 3B42RT estimates before and after assimilation by using a Kalman filter with independent rain gauge networks located within the Jinghe basin of China. Generally, the direct comparison of TMPA precipitation estimates to 200 collocated rain gauges from 2006 to 2008 demonstrate that the spatial and temporal rainfall characteristics over the region are well captured by the assimilation estimates. Especially, results also show that using Kalman filter to assimilate TRMM-based multi-satellite real-time precipitation estimates tends to perform well over regions, where gauge network is rather sparse. Last, this study highlights that accurate detection and estimation of precipitation in the summer season by Kalman filter, particularly for nonlinear convective precipitation events, is still a challenging task for the future development of assimilation technique for improving the satellite-based precipitation accuracy.

1. Introduction

Precipitation is one of the most important forcing variables for hydrologic and climatic models, and therefore accurate measurement of precipitation is crucial for a comprehensive understanding of the climate and hydrology cycles at local, regional, and even global scales [1,2,3]. Traditionally, rain gauges are widely used in rainfall measurement, but unfortunately, typical densities of operational rain gauge networks are usually unable to fulfill the requirements for surface precipitation monitoring especially in remote regions, ungauged basins, or areas with complex terrain [4,5]. Although weather radar can monitor the surface precipitation with relatively high resolution [6], it suffers from some error problems associated with backscatter, attenuation and extinction of signal, bright band effects, and uncertainty of the Z–R relationship [7]. Thus, satellite-based remote sensing plays an important role in detecting the regional or global rainfall distributions from space and has been complementary to the ground-based rain gauge and radar measurements.

Since the launch of the Tropical Rainfall Measuring Mission (TRMM) in 1997, a growing number of multi-sensor and quasi-global satellite precipitation estimates have been produced for a variety of scientific research and disaster warning. These operational TRMM-era rainfall products mainly include the TRMM Multi-satellite Precipitation Analysis (TMPA) [8,9], the NOAA/Climate Prediction Center (CPC) morphing technique (CMORPH) [10], Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks (PERSIANN) [11,12], and the JAXA’s Global Satellite Mapping of Precipitation (GSMaP) [13]. With the splendid success of TRMM, the Global Precipitation Measurement (GPM) Core Observatory was launched in February 2014 to provide next-generation global rain as well as snow observations in near-real-time [14,15]. Currently, two GPM-based high resolution satellite precipitation estimates, namely Integrated Multi-satellite Retrievals for GPM (IMERG) and Global Satellite Mapping of Precipitation (GSMaP) version 6, are released [16]. The concept behind most of these multi-sensor retrieval algorithms relies upon the merging of passive microwave (PMW)- and infrared (IR)-based estimates. They offer an alternative source of rainfall information for vast areas of Earth’s surface, and also pose significant challenges for hydrologists and meteorologists in applying these new satellite data to their regional or local applications.

As a typical example, the operational TMPA real-time product 3B42RT, which combines the high-quality passive microwave and microwave-calibrated geostationary infrared, provides 3 hourly, 0.25° × 0.25° latitude/longitude gridded precipitation data starting from 1 March 2000 to present [16]. It is the long-term data availability (over 16 years) and relatively fine resolution that make 3B42RT more potential in hydrologic simulation and prediction at large scale [17,18]. This TRMM-based user-level real-time rainfall product has been widely used in many applications, but their error and uncertainty characteristics over diverse regimes still need to be quantified [19,20,21,22,23,24,25]. Intercomparison of rainfall estimates from satellite retrievals and ground observations is an important means to assess the confidence in satellite algorithms, which provides a benchmark for their future development and improvement. In many prior studies, the data errors of those TRMM-based multi-satellite precipitation estimates have been extensively investigated by using ground-based gauges and radars to serve as the reference over different regions [26,27,28,29,30].

The errors of satellite precipitation estimation arise from different factors including the sensor itself, retrieval error, and spatial and temporal sampling, among others [31]. The systematic and random errors caused by these factors need to be quantified and modified. This could help both algorithm developers and data users to better understand the error features of satellite precipitation and their generation mechanisms. Considering the significant impacts of systematic error at larger spatiotemporal scales, the TMPA data developers applied a month-to-month gauge adjustment into the real-time processing system and produced the post-real-time research-grade product 3B42 [32,33]. For this monthly adjustment procedure, the large-scale systematic errors can be removed better. However, this monthly gauge calibration cannot reduce the random error at the daily or sub-daily scales. Moreover, when removing systematic bias at the monthly scales, the correction scheme might bring deleterious effects on the small-scale rainfall accumulations [34]. Thus, the purely satellite-derived precipitation estimates were provided by the TMPA developers as an additional field in the TMPA real-time data set. Such satellite-only information allows the TMPA users to employ local high-resolution surface observations or other information in assimilating and correcting the uncalibrated TMPA to create new precipitation products appropriate to the user’s local application. For example, Ciabatta et al. [35] integrated TMPA 3B42RT and a new soil moisture dataset based rainfall product over the Italian territory, which demonstrates a significant improvement of the agreement with a high density gauge-based rainfall dataset.

However, in terms of the current literatures, the correction techniques (e.g., Kalman filtering) are mainly used to remove the mean rainfall field bias of ground-based radar measurements rather than assimilation of satellite precipitation [36,37,38,39,40,41,42,43]. As is well known, radar measurements perform significantly worse in complex terrain and mountainous areas because of ground clutter and beam blockage. Satellite-based remote sensing can offer quasi-global rainfall information without terrain restriction. In this paper, we attempt to study the adaptability of the Kalman filter approach in correcting the real-time TRMM precipitation estimates at a medium-sized basin. A 3-year Version-7 3B42RT data and ground rain gauge records in Chinese Jinghe basin are chosen to test the efficiency of the Kalman filter assimilation, while the parametric sensitivity of a Kalman filter is also comprehensively analyzed.

In the next section, we describe the study area and the datasets used. The detailed methodologies are demonstrated in Section 3. A presentation of the assimilation results and analyses follows in Section 4. Summarizing remarks and conclusions finalize the paper in Section 5.

2. Study Area and Data

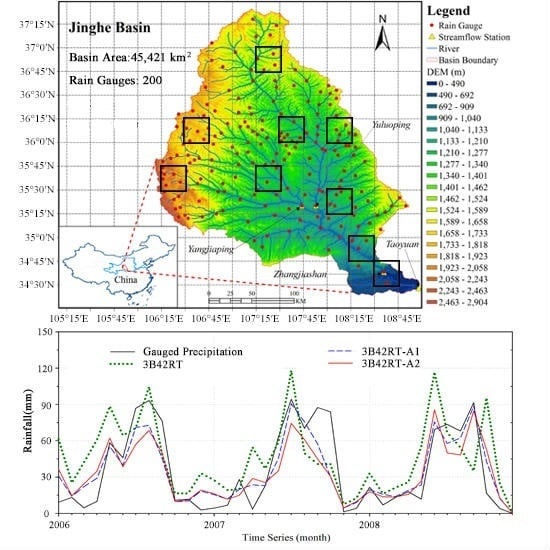
2.1. Jinghe Basin

The Jinghe basin, with a drainage area of 45,421 km², is located at the junction of Gansu, Shanxi Provinces and Ningxia Hui Autonomous Region in the northwest of China (Figure 1). The basin lies at latitude of 34°46′–37°19′N and longitude of 106°14′–108°42′E with a typical semiarid climate. The average annual temperature, precipitation, and runoff in this area were 8 °C, 539.1 mm, and 18.32 mm, respectively. The basin elevation ranges from 350 m above sea level at the channel outlet to over 2900 m in the upstream mountainous area, and the topography significantly descends from northwest to southeast. As for the ground-based rainfall gauge observation, both the China Meteorological Administration (CMA) and the Chinese Ministry of Water Resources (CMWR) operate all rain gauge networks over the entire mainland China including our study basin. Two types of methods, i.e., tipping-bucket rain gauge and manual traditional ombrometer, are used by local workers to record the rainfall events in practice. Then these two types of recorded data are crosschecked and the final errors have to be controlled within 4% for daily rainfall observation according to the ministerial standard. Compared to other basins in the northern part of China, Jinghe basin has an extraordinarily dense observation network of 200 conventional rain gauges maintained by the CMWR which can provide relatively reliable ground verification for the satellite precipitation estimates. Meanwhile, in this basin, the daily meteorological observations can be obtained from 13 CMA stations, including daily precipitation, wind speed, mean air temperature, relative humidity, hours of sunshine, and so on. Hence, these two sets of ground data are from different sources and independent from each other. Considering both spatial distributions and gauge numbers, we choose nine 0.25° × 0.25° gridboxes for the grid-based verification of satellite precipitation estimates in our study. These 9 representative grids are displayed in Figure 1 with black squares.

2.2. NASA TMPA

In the present implementation, the TMPA real-time (TMPA-RT) algorithm combines microwave (MW) and the infrared precipitation (IR) precipitation estimates and provides the high-resolution multi-sensor blended precipitation satellite products to accommodate different needs for a wide range of researchers and users [16]. For the TMPA system, the polar-orbiting microwave information is collected by a variety of low earth orbit satellites, including Special Sensor Microwave Imager (SSM/I) on Defense Meteorological Satellite Program (DMSP) satellites, Advanced Microwave Scanning Radiometer-Earth Observing System (AMSR-E) on Aqua, and the Advanced Microwave Sounding Unit-B (AMSU-B) on the National Oceanic and Atmospheric Administration (NOAA)-15, 16, and 17 satellites. The second type of data source for 3B42RT is the gap-filling infrared (IR)-based estimates merged from five geosynchronous earth orbit (GEO) satellites into half-hourly 4 km × 4 km equivalent latitude-longitude grids.

On 28 January 2013, the latest Version-7 TMPA-RT data (hereinafter referred to as 3B42RT; 2000–now) were formally released so as to provide the users a new backlog for validation and application activities. This product is a near-real-time product with 3-hourly, 0.25° resolution over a global latitude band 50°NS which computed about 6–9 h after observation time. Relative to original Version-6, the new Version-7 TMPA system introduces some additional data sources, including the Special Sensor Microwave Imager/Sounder (SSMIS) (F16 and F17) and Microwave Humidity Sounder (MHS) (N18 and N19) and Meteorological Operational satellite programme (MetOp) and the 0.07° Grisat-B1 infrared data.

3. Methodology

3.1. Preprocess

The process of Kalman filter assimilation used in our study is summarized in Figure 2, which can be divided into three parts: preprocess, time update, and measurement update. During the preprocess stage, the GIS-based interpolation techniques were first adopted to generate continuous surfaces of precipitation over the entire basin. In this paper, the 0.25° × 0.25° gridded TMPA products were interpolated onto 0.0625° resolution data sets for the Jinghe basin by using a simple cropping approach proposed by Hossain and Huffman (2008) [44], while the 200 gauge observations were interpolated onto the same grid by using the Inverse Distance Weighting (IDW) interpolation method. IDW is a classic interpolation method which has been widely applied in the fields of GIS and remote sensing [45,46]. The main advantage of this approach is excellent stability and robustness in the practical operations. Specific details of the IDW are given in Appendix A.

After the interpolation, the data from ground rainfall station and TMPA estimates could be unified at the same scale (denoted as $G_t$ and $S_t$ in the flow chart, respectively). Then, a statistical method was used to remove the mean field bias (defined as $x_t=\frac{G_t}{S_t}$) between TMPA estimates at the rain gauge locations and the corresponding gauge rainfall amounts [41,42]. In this study, the errors between TMPA rainfall estimates and rain gauge measurements are considered to be spatially uniform, while this bias exhibits evident persistence and can be modeled as a stationary Makovian process [38,39,40]. As a result, the mean field bias, $x_t$, could be characterized as an autoregressive order one (AR1) model [41], with parameters being updated by using a Kalman filter. Details on the steps involved in the time and measurement update stages of the Kalman filter technique are presented in the next sub-section.

3.2. Time Update

The second stage of the Kalman filter, namely time update, primarily consists of projecting the mean field bias and the associated error variance to the current time step, which is continuously illustrated in Figure 2. As the lack of knowledge of the time varying behavior of the daily mean field bias (specifically for the TRMM-based 3B42RT estimates here), $x_t$ is usually assumed to follow an AR1 process [39], represented as:

$$x_t=A{x}_{t-1}+B_t$$

(1)

where $A$ is the lag-one correlation coefficient of the mean field bias, and $B_t$ is an independent normally distributed random variable with mean zero. Thus, a priori estimate of $x$ can be estimated as:

$${\widehat{x}}_t=A{\widehat{x}}_{t-1}$$

(2)

which provides the basis for formulating the estimate $\widehat{x}$ that takes into account the new measurement that is observed, and corrects for any errors that may be present in the newly measured value.

A priori estimate of the variance of $B_t$ referred to as the process variance and denoted $P_t^{-}$ in Figure 2 can be calculated as:

$$P_t^{-}=A{P}_{t-1}{A}^T+Q$$

(3)

where P_t−1 is a posteriori estimate error variance at time t − 1, and Q is the process error variance.

3.3. Measurement Update

The third stage of the assimilation involves updating a priori estimate of the mean field bias ${\widehat{x}}_t^{-}$ and the variance $P_t^{-}$ based on the actual measurement for the current time step t. The estimated mean field bias and process variance after this stage for time step t will be denoted ${\widehat{x}}_t$ and $P_t$, respectively. The error of the observed rain field contains a deviation ($x$) between the observed and true values. Denoting $x_t$ as the observed mean field bias at time t, and the measurement update of the Kalman filter allows estimation of ${\widehat{x}}_t$ and $P_t$ as detailed in the following equations:

$${\widehat{x}}_t={\widehat{x}}_t^{-}+K_t(x_t-{\widehat{x}}_t^{-})$$

(4)

$$P_t=(1-K_t)P_t^{-}$$

(5)

$$K_t=P_t^{-}{(P_t^{-}+R)}^{-1}$$

(6)

where $K_t$ is known as the Kalman gain, and $R$, which is called observation error variance, represents the time varying variance of ($z_t-x_t$). More details about the Kalman filter can be found in [36,37].

4. Results and Analysis

4.1. Implementation of Kalman Filter in Jinghe Basin

Our evaluation and comparison were performed over two domains including nine selected 0.25° × 0.25° grids (labeled with black box in Figure 1) corresponding to TRMM pixel resolution, as well as the basin-averaged analysis. The basin-averaged data comparison is a very appropriate approach for presenting the whole average error over a region, while grid-based comparison can accurately exhibit the error features of several representative grids distributed with relatively denser gauges.

In this study, the nine nested grid locations were chosen because each of them contains at least two rain gauges and these selected grids relatively evenly distributed throughout the entire basin (“Grid0401”, “Grid0402” and “Grid0601” located at the upstream of our basin; “Grid0801”, “Grid0501” and “Grid0301” at the midstream; “Grid0502”, “Grid0302” and “Grid0201” at the downstream). There exist significant terrain differences between these nine grids; therefore, versatility and robustness of proposed assimilation technique could be inspected. The rain gauge accumulations from each gauge are averaged within each TRMM pixel so that they can be compared to the TMPA-RT estimates, as well as assimilation results. Next, efforts will be focused on investigating the performance of the Kalman Filter assimilation at daily, monthly, and seasonal time scales, respectively.

4.1.1. Basin-Averaged Comparison

In this basin-averaged analysis, the observed rainfall data collected from 200 rain gauges of CMWR were used to correct the 3B42RT products from 2006 to 2008 over the Jinghe basin. To quantify the accuracy of assimilations, we adopted four types of validation statistical indices including correlation coefficient (CC), root mean square error (RMSE), mean error (ME), and relative bias (BIAS). The CC was used to assess the agreement between the assimilation precipitation and rain gauge observations, while the RMSE was used to measure the average error magnitude. The ME was used to scale the average difference between the assimilation precipitation and rain gauge observations, whereas the BIAS describes the systematic bias. Their formulas are stated as:

$$\text{CC}=\frac{{\sum }_{i=1}^n\left(G_i-\overline{G}\right)\left(S_i-\overline{S}\right)}{\sqrt{{\sum }_{i=1}^n{\left(G_i-\overline{G}\right)}^2\sqrt{{\sum }_{i=1}^n{\left(S_i-\overline{S}\right)}^2}}}$$

(7)

$$\text{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\left(S_i-G_i\right)}^2}$$

(8)

$$\text{ME}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}\left(S_i-G_i\right)$$

(9)

$$\text{BIAS}=\frac{{\sum }_{i=1}^n\left(S_i-G_i\right)}{{\sum }_{i=1}^n{G}_i}\times 100\%$$

(10)

where n is the total amount of rain gauge or satellite precipitation data; S_i and G_i are the ith values of the satellite (or assimilation) precipitation data and rain gauge observations, respectively; and $\overline{S}$ and $\overline{G}$ are the mean values of the assimilation (or satellite) precipitation data and rain gauge observations, respectively.

In addition, three categorical statistical indices, including the probability of detection (POD), false-alarm rate (FAR), and critical success index (CSI), were adopted to measure the correspondence between the satellite precipitation products and rain gauge observations. POD, also known as the hit rate, represents how often the rain occurrences are correctly detected by the satellite. FAR denotes the fraction of cases in which the satellite records precipitation when the rain gauges do not. CSI shows the overall fraction of precipitation events correctly diagnosed by the satellite. The perfect values of POD, FAR and CSI were 1, 0, and 1, respectively. The formulas are given by:

$$\text{POD}=\frac{t_H}{t_H+t_M}$$

(11)

$$\text{FAR}=\frac{t_F}{t_H+t_F}$$

(12)

$$\text{CSI}=\frac{t_H}{t_H+t_M+t_F}$$

(13)

where H, M, and F are different cases: H, observed rain correctly detected; M, observed rain not detected; F, rain detected but not observed; and t_H, t_M, and t_F are the times of occurrence of the corresponding case; rain or no-rain events were defined by the value of the threshold, and a precipitation threshold of 1.0 mm was used in this study. The details of these statistical indices can refer to Ebert [27].

Figure 3a,b show the daily precipitation difference before and after application of the Kalman Filter assimilation to 3B42RT for the basin-averaged comparison. Our evaluation results indicate that this is a significant improvement for the satellite precipitation estimates after the assimilation. Taking the daily comparison for example, the CC value increases from 0.63 of original 3B42RT to 0.75 of assimilated data and meanwhile the error and bias also correspondingly decreases after assimilation (e.g., RMSE with 2.57 mm versus 2.05 mm, ME with 0.34 mm versus −0.03 mm, BIAS with 29.1% versus −2.37%). More significant improvement can be found in the monthly scatterplots (see Figure 3c,d).

During the process of above Kalman filtering assimilation, five parameters need to be defined. They are TRMM rainfall bias (${\widehat{x}}_t$), estimate error variance ($P_t$), process error variance ($Q$), observation error variance ($R$), and Kalman gain ($K_t$), respectively. It is conceivable that the final assimilation results might be evidently different if the values of any sensitive parameter change. Thus, it is necessary to test the sensitivity of these parameters to find the optimal parameters in order to obtain the best assimilation effect. Furthermore, the influence analysis of parameter variations will contribute to verifying the suitability and robustness of assimilation method, and then provide important guidance for the future applications. In order to simplify the analysis, in our experiments, $A$ in Formula (2) is denoted as the unit matrix, and variation range of five parameters is set between 0.1 and 0.9 (with an interval step of 0.1). During the following parameter sensitivity analysis, ${\widehat{x}}_t$ is the first parameter to be studied, while all the initial values of other four parameters are set to 0.5. With the changing values of ${\widehat{x}}_t$, the results of assimilation might correspondingly vary too. The best optimal parameter is benchmarked by the minimum RMSE value obtained in the assimilation. Thus, the optimum value of ${\widehat{x}}_t$ can be worked out according to this benchmark. Then, maintaining the optimal parameter value ${\widehat{x}}_t$ unchanged, we can successively analyze the rest four parameters using the same approach.

Figure 4 shows the sensitivity analysis results of these five key parameters for basin-average. It shows that two most sensitive parameters in the Kalman filter assimilation are bias estimate (${\widehat{x}}_t$) and Kalman gain ($K_t$), respectively. As is well known, ${\widehat{x}}_t$ defines estimate of daily mean field TRMM rainfall bias, thus an increase of ${\widehat{x}}_t$ in the Kalman filter means that the measurement error is smaller than the difference between satellite estimates and gauge observations. In the assimilation process, $K_t$ chiefly controls the balance between ${\widehat{x}}_t^{-}$ (a priori estimate of the mean field bias) and $z_t$ (observed mean field bias). For extreme instance, $K_t=1$ represents that the estimated mean field biases equal to the observed mean field biases (${\widehat{x}}_t=z_t$), which means a priori information does not play a crucial role in the assimilation process. On the other hand, $K_t=0$ (${\widehat{x}}_t={\widehat{x}}_t^{-}$) indicates there is no input of observed mean field bias. For our study basin, a value of ${\widehat{x}}_t$ between 0.4 and 0.7 and a value of $K_t$ between 0.1 and 0.3 can produce higher CC and lower RMSE for the high density assimilation, while other three tested parameters (i.e., $R$, $Q$ and $P_t$) show less sensitivity within their typical ranges.

4.1.2. Grid-Based Comparison

In this section, the gridded 3B42RT product and its assimilated data will be compared with the point-scale gauge data. To reduce the scale errors, grid boxes were only selected which contained at least two gauges and then used the mean value of all gauges inside each grid box as the ground truth [47,48]. The nine selected grids are shown in Figure 1. The original and assimilated satellite precipitation of 3B42RT over those selected grid boxes were compared against gauge observations, and the statistical indices (i.e., CC, RMSE, ME, and BIAS) are shown in Figure 5.

Similar to the basin-averaged results in Figure 3, the grid-based comparison demonstrated that the precipitation data after assimilation had a better performance than original 3B42RT for selected grid locations with improved correlation and reduced bias ratio. As expected, the statistics of the grid-based comparisons are generally worse than those of the basin-averaged data. For both daily and monthly scales, better CC values and lower BIAS were found in assimilated results than in original 3B42RT data. The daily scatterplots show that the BIAS of 3B42RT and assimilated data against gauge observations are 34.39% and −22.56%, and their correlation coefficients are 0.49 and 0.53, respectively (Figure 5a,b). Additionally, the monthly scatterplots (Figure 5c,d) also show that assimilated results largely outperformed RT with higher correlation (0.64 versus 0.49) and lower error (−8.00 versus 12.18 mm for ME). Figure 6 shows the sensitivity test results of grid-based assimilation experiment. Similar to the basin-averaged analysis, ${\widehat{x}}_t$ and $K_t$ are still the most sensitive parameters in the assimilation process, while other three parameters are insensitive.

4.2. Assimilation Results with Sparse Gauges

Hydrology has been a data-limited science, while most of the fluxes and components in the hydrologic cycle are difficult to directly measure. Even readily measured hydrologic variables are typically available only at isolated locations or times. Using space-time estimation of rainfall from satellite remote sensing provides an alternative approach to area-wide precipitation forecasting at any location with or without ground-based observations. However, satellite estimates of rainfall may lack consistent, quantitative accuracy. A combination between satellite estimates and ground observations will significantly improve the data accuracy of available rainfall information. Thus, next we attempt to explore the ways how to improve the TRMM retrieval accuracy using Kalman filter method with rare rain gauge network.

In this study, the scarce observed daily precipitation data from 2006 to 2008 were recorded by the 13 meteorological stations distributed within the Jinghe basin (Figure 7). By utilizing the same assimilation technique mentioned above, the assimilation effect in basin-averaged case is still quite good, while 13 independent CMA stations replaced 200 CMWR gauges as assimilation data source. As a result, the overall improvement in rainfall estimation could be found in assimilation experiments even in the scarce station status (Figure 8). This further confirms the validity and potential applications of this assimilation approach for rainfall retrievals in rare gauge data area.

For this assimilation experiment based on the scarce national meteorological stations, Figure 9 demonstrates the sensitivity testing results of key assimilation parameters. It is obvious that five important parameters basically have the similar sensitivity law in three simulations, which are summarized in

Table 1. The Results of Sensitivity Analysis for Assimilation Parameters in Jinghe Basin.

		${\widehat{\mathit{x}}}_{\mathit{t}}$	${\mathit{P}}_{\mathit{t}}$	$\mathit{Q}$	$\mathit{R}$	${\mathit{K}}_{\mathit{t}}$
OP	Experiment I	0.6	0.1	0.1	0.1	0.2
	Experiment II	0.4	0.1	0.1	0.2	0.2
	Experiment III	0.6	0.1	0.1	0.5	0.2
SR	Experiment I	13.71%	0.24%	0.25%	1.08%	45.71%
	Experiment II	15.59%	0.30%	0.30%	0.31%	30.32%
	Experiment III	10.97%	2.43%	3.77%	2.39%	30.78%

Note: In the text, Experiments I, II, III represents basin-averaged assimilation with high density stations, grid-based assimilation with high density stations, and basin-averaged assimilation with low density stations. Respective optimal values of five parameters in experiments could be found in the column of “Optimal Parameter (OP)”, when minimum RMSE is the criterion. “Sensitive Range (SR)”, which reflects the relative error of RMSE in assimilation resulting from the worst and optimal parameter value, is defined as: $SR=\frac{RMS{E}_{wp}-RMS{E}_{op}}{RMS{E}_{op}}\times 100\%$, where $RMS{E}_{op}$ is the RMSE value with optimal parameter and $RMS{E}_{wp}$ is the RMSE value with worst parameter. More comprehensive presentation is shown in Figure 4, Figure 6 and Figure 9.

. The results of the sensitivity analysis demonstrate that the most sensitive parameters in the Kalman filter assimilation are still the bias estimate (${\widehat{x}}_t$) and the Kalman gain ($K_t$). For our study basin, a value of ${\widehat{x}}_t$ between 0.4 and 0.7 and that of $K_t$ ranging from 0.1 to 0.3 produce higher correlation coefficient and lower root mean squared error in assimilation consequent. For example, in experiment III, when ${\widehat{x}}_t$ ($K_t$) takes the worst value, the RMSE might deteriorate 10.97% (30.78%) compared to the best assimilation results. On the contrary, the other three parameters $R$, $Q$ and $P_t$ show much less sensitivity (The maximum RMSE is approximately 3%) within their typical ranges, which require minor adjustment during the assimilation process.

4.3. Seasonal Analysis

Figure 10 depicts the time series of monthly mean precipitation of Jinghe basin from January 2006 to December 2008 for gauge reference (black line), original 3B42RT (green line), and corrected 3B42RT assimilated with high density (A1—200 hydrological stations) (blue line) and with low density (A2—13 meteorological stations) (red line), respectively. According to our experiments, we concluded that (1) compared with the measurement data of ground station, estimate results of 3B42RT are overall higher; (2) assimilation data gives the best performance and seems to work well even with scarce ground data; (3) the results of high density and low density assimilation are similar, which suggests the robustness of the assimilating technique. Note that the above conclusions are based on an intuitive truth. Next, we conduct the specific seasonal analyses to illustrate the effect of the filter performance and further confirm our conclusions.

Table 2. Statistical Summary of the Seasonal Comparison of Basin Average and Grid-Based Precipitation Estimates between 3B42RT and Assimilation in Jinghe Basin.

		CC		RMSE		BIAS
		RT	New	3B42RT	New	3B42RT	New
Spring	Basin Average (H)	0.58	0.64	2.12	1.47	1.37	0.35
	Basin Average (L)	0.58	0.63	2.12	1.52	1.37	0.45
	Grid Based	0.43	0.48	3.52	2.27	1.42	0.27
Summer	Basin Average (H)	0.80	0.78	2.67	2.85	0.06	−0.11
	Basin Average (L)	0.80	0.69	2.67	3.27	0.06	−0.22
	Grid Based	0.58	0.59	6.24	5.64	0.07	−0.38
Autumn	Basin Average (H)	0.32	0.74	3.55	2.34	−0.15	−0.21
	Basin Average (L)	0.32	0.70	3.55	2.44	−0.15	−0.22
	Grid Based	0.35	0.48	5.30	3.74	−0.07	−0.40
Winter	Basin Average (H)	0.18	0.24	1.49	1.01	2.29	0.95
	Basin Average (L)	0.18	0.18	1.49	1.05	2.29	1.02
	Grid Based	0.12	0.11	2.43	1.69	2.27	0.81

Note: In this table, Basin Average (H) means the basin average assimilation with high-density 200 rain gauges, Basin Average (L) means the basin average assimilation with low-density 13 meteorological stations. Four seasons are defined as: spring (March–May), summer (June–August), autumn (September–November), and winter (December–February).

shows the statistical summary of the seasonal precipitation estimates comparison between original 3B42RT estimates and those with high (or low) density assimilations in Jinghe basin, respectively. Comparisons in Table 2 demonstrate that assimilation products (refer to as “New” in the table) had a better performance than 3B42RT for most seasons (except summer) at both basin average and grid based cases with significantly improved CC and BIAS (especially in autumn). Similar trend can be also found in Table 2 for low density assimilation analysis. However, the results of assimilation for summer are not satisfactory. The chief reason might be caused by point measurements of rain gauges, which cannot capture well the convective summer storms with high local variability, especially over those regions with relatively sparse rain gauges. Another possible explanation is that the summer season rainfall contradicts with these assumptions in Kalman filter assimilation process. In this study, the TRMM rainfall bias in the Kalman filter method is assumed spatially invariant, and a stationary Markovian process, while the mean field bias $Z_t$ could be characterized as an autoregressive order one (AR1) model. This assumption may be appropriate for spring, autumn and winter, which dominant precipitation type is stratiform rain. However, for a high proportion of convective precipitation in summer season rainfall, this assumption may no longer be established.

4.4. Discussion

By merging the most available PMW and IR satellite retrievals, the TRMM-based TMPA system produces a high-resolution precipitation product 3B42RT, which is attractive to a wide range of hydrological applications, such as flood forecasting and landslide warning. However, the current TMPA estimates are still affected by systematic and random errors that need to be corrected by local high quality ground observations. As one of the most important improvements during precipitation measurement, the assimilation methods were regarded as an operational approach that can introduce ground-based gauge information to effectively reduce the systematic and random errors, while maintaining the near-real-time availability of 3B42RT itself.

In this study, a Kalman filtering assimilation approach is proposed for correcting the bias of the real-time TRMM 3B42RT rainfall estimates for a period of three years (2006 to 2008) in a Chinese medium-sized and semi-arid basin. This assimilation model is simple but robust, while the mean field bias was assumed to follow an autoregressive order one structure. Compared to the month-to-month gauge adjustments in the post-real-time TMPA estimates provided by the data developers, the proposed technique operates more efficient especially for local and regional rainfall estimation. Furthermore, sensitivity analysis of assimilation parameter improves the adaptability and robustness of the proposed method. The ideal combination of parameters can be determined after specific analysis in the practical applications.

Additionally, our study suggests that the assimilation process is rather sensitive to the density of rainfall gauges in summer. This could be caused by point measurements of rain gauges, which cannot detect well the convective storms with high local variability. Thus, the gauge assimilation for summer requires denser gauge networks to capture the peaks of extreme rainfall events. In particular, over those specific regions where the convective rainfall events frequently occurred, it might be better for users to directly use the satellite products without any assimilation correction.

5. Summary

In this study, we compared and validated the standard Tropical Rainfall Measuring Mission (TRMM) Multi-satellite Precipitation Analysis (TMPA) product, Version-7 3B42RT, before and after assimilation using Kalman filter with independent rain gauge networks located within the Jinghe basin of China. The principal findings of this study are summarized as follows.

(1)

Relative to gauge observations, the satellite precipitation estimation 3B42RT shows a large positive bias in the study basin. The results of our numerical experiments indicate that the assimilated precipitation estimates with Kalman filtering approach significantly outperform the original 3B42RT product before assimilation, even when the number of rain gauges used in the assimilation is fairly limited. Therefore, we concluded that the Kalman filter assimilation has great potential to improve the data accuracy of purely satellite precipitation retrievals, especially over the data sparse area.

(2)

The sensitivities of five Kalman filter parameters are analyzed for further understanding the assimilation process. Our analysis shows that two most sensitive parameters in the assimilation are mean field bias (${\widehat{x}}_t$) and Kalman gain ($K_t$), respectively, while other three parameters, i.e., estimate error variance ($P_t$), observation error variance ($R$), and process error variance ($Q$), have less sensitivity. It should be noted that the bias of four seasons seems to be averaged after assimilation. This might be caused by the continuous assimilation on multi-year time scales, which results in the homogenization of the statistical properties. This might be also the reason that causes the insensitivity of parameters R and Q. If the same assimilation method is solely applied for summer rainstorms, such situation might be changed.

(3)

In addition, our assessment illustrates that the Kalman filter seems to perform rather well in autumn, in which it can effectively reduce the error and bias of original 3B42RT and improve the skill of detecting rainy events. However, we have to note that the assimilation results in summer become relatively worse. The seasonal analysis and comparison with high and low density assimilation estimates also display that the situation of other seasons is obviously different from that in summer. For example, the RMSEs of low density assimilation were reduced by 3.40%, 4.27%, 3.96%, for spring, autumn and winter, respectively, while the dramatic deterioration by 14.74% was occurred in summer.

In summary, we expect that the analysis results reported here can provide a better understanding of the error characteristics and application potentials of the satellite-based remote sensing precipitation assimilation. Although all the results drawn from this study may be specific to the medium-sized Jinghe basin over Mainland China, they are likely to be also applicable to other similar areas in the world. Specifically, our evaluation highlights the need for caution when using the Kalman filter to assimilate satellite precipitation estimates for monitoring heavy rainfall-related hydrologic extremes. Based on our findings, we recommend that the future correction efforts should focus on integrating different rainfall information (such as meteorological radar and weather model outputs) to further improve the retrieval accuracy of satellite precipitation retrievals, especially for those extreme rainfall events occurred in summer.