An Algorithm for In-Flight Spectral Calibration of Imaging Spectrometers
Abstract
:1. Introduction
2. Data
2.1. Synthetic Data
2.2. Real Data from the APEX Imaging Spectrometer
3. Spectral Calibration Algorithm: General Framework and Application to APEX
3.1. General Framework
3.1.1. Forward Model
3.1.2. Maximum A Posteriori Retrieval
3.2. APEX Spectral Calibration Algorithm
3.2.1. Forward Model
3.2.2. Instrument and Forward Model Errors
3.2.3. A Priori State Vector Errors and Regularization
4. Results
4.1. Degrees of Freedom
4.2. Smoothing Errors
4.3. Performance with Synthetic Spectra
4.4. Performance with APEX Measurements
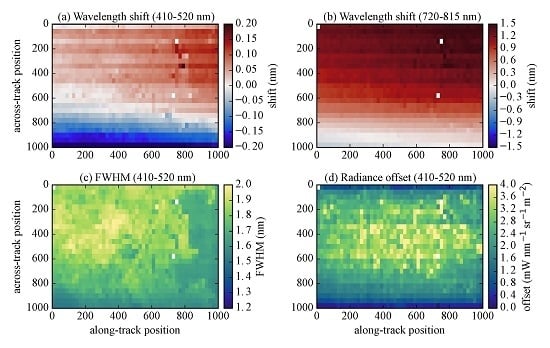
4.4.1. Spectral Residuals
4.4.2. Wavelength Shift
4.4.3. Instrument Slit Function (FWHM) and Radiance Offset
5. Discussion
5.1. Usefulness of the Algorithm
5.2. Potential Improvements of the Algorithm
5.3. Challenges and Issues Related to the Analysis of Real Data
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hochberg, E.J.; Roberts, D.A.; Dennison, P.E.; Hulley, G.C. Special issue on the Hyperspectral Infrared Imager (HyspIRI): Emerging science in terrestrial and aquatic ecology, radiation balance and hazards. Remote Sens. Environ. 2015, 167, 1–5. [Google Scholar] [CrossRef]
- Schaepman, M.E.; Jehle, M.; Hueni, A.; D’Odorico, P.; Damm, A.; Weyermann, J.; Schneider, F.D.; Laurent, V.; Popp, C.; Seidel, F.C.; et al. Advanced radiometry measurements and Earth science applications with the Airborne Prism Experiment (APEX). Remote Sens. Environ. 2015, 158, 207–219. [Google Scholar] [CrossRef]
- Popp, C.; Brunner, D.; Damm, A.; Van Roozendael, M.; Fayt, C.; Buchmann, B. High-resolution NO2 remote sensing from the Airborne Prism EXperiment (APEX) imaging spectrometer. Atmos. Meas. Tech. 2012, 5, 2211–2225. [Google Scholar] [CrossRef]
- Laurent, V.C.; Verhoef, W.; Damm, A.; Schaepman, M.E.; Clevers, J.G. A Bayesian object-based approach for estimating vegetation biophysical and biochemical variables from {APEX} at-sensor radiance data. Remote Sens. Environ. 2013, 139, 6–17. [Google Scholar] [CrossRef]
- Damm, A.; Guanter, L.; Paul-Limoges, E.; van der Tol, C.; Hueni, A.; Buchmann, N.; Eugster, W.; Ammann, C.; Schaepman, M. Far-red sun-induced chlorophyll fluorescence shows ecosystem-specific relationships to gross primary production: An assessment based on observational and modeling approaches. Remote Sens. Environ. 2015, 166, 91–105. [Google Scholar] [CrossRef]
- Platt, U.; Stutz, J. Differential Optical Absorption Spectroscopy: Principles and Applications; Springer: Heidelberg, Germany, 2008. [Google Scholar]
- Damm, A.; Erler, A.; Hillen, W.; Meroni, M.; Schaepman, M.E.; Verhoef, W.; Rascher, U. Modeling the impact of spectral sensor configurations on the FLD retrieval accuracy of sun-induced chlorophyll fluorescence. Remote Sens. Environ. 2011, 115, 1882–1892. [Google Scholar] [CrossRef]
- Caspar, C.; Chance, K. GOME wavelength calibration using solar and atmospheric spectra. In Proceedings of the Third European Remote Sensing Satellite Scientific Symposium: Space at the Service of our Environment, Florence, Italy, 17–20 March 1997; Guyenne, T.D., Danesy, D., Eds.; European Space Agency: Noordwijk, The Netherlands, 1997; pp. 609–614. [Google Scholar]
- Van Geffen, J.H.; van Oss, R.F. Wavelength calibration of spectra measured by the Global Ozone Monitoring Experiment by use of a high-resolution reference spectrum. Appl. Opt. 2003, 42, 2739–2753. [Google Scholar] [CrossRef] [PubMed]
- Gao, B.C.; Montes, M.J.; Davis, C.O. Refinement of wavelength calibrations of hyperspectral imaging data using a spectrum-matching technique. Remote Sens. Environ. 2004, 90, 424–433. [Google Scholar] [CrossRef]
- Schläpfer, D.; Schaepman, M.; Bojinski, S.; Börner, A. Calibration and validation concept for the airborne prism experiment (APEX). Can. J. Remote Sens. 2000, 26, 455–465. [Google Scholar] [CrossRef]
- Hueni, A.; Lenhard, K.; Baumgartner, A.; Schaepman, M. Airborne Prism Experiment Calibration Information System. IEEE Trans. Geosci. Remote Sens. 2013, 51, 5169–5180. [Google Scholar] [CrossRef] [Green Version]
- Jehle, M.; Hueni, A.; Lenhard, K.; Baumgartner, A.; Schaepman, M. Detection and Correction of Radiance Variations During Spectral Calibration in APEX. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1023–1027. [Google Scholar] [CrossRef]
- D’Odorico, P.; Guanter, L.; Schaepman, M.E.; Schläpfer, D. Performance assessment of onboard and scene-based methods for Airborne Prism Experiment spectral characterization. Appl. Opt. 2011, 50, 4755–4764. [Google Scholar] [CrossRef] [PubMed]
- Kuhlmann, G.; Hueni, A.; Damm, A.; Brunner, D. In-flight spectral calibration of the APEX imaging spectrometer using Fraunhofer lines. In Proceedings of the ESA ATMOS 2015, University of Crete, Heraklion, Greece, 8–12 June 2015.
- Danckert, T.; Fayt, C.; Van Roozendael, M.; De Smedt, I.; Letocart, V.; Merlaud, A.; Pinardi, G. QDOAS Software. 2015. Available online: http://uv-vis.aeronomie.be/ (accessed on 21 April 2016).
- Jenkins, F.A.; White, H.E. Fundamentals of Optics; Tata McGraw-Hill Education: New York, NY, USA, 1957. [Google Scholar]
- Mayer, B.; Kylling, A. Technical note: The libRadtran software package for radiative transfer calculations-description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Emde, C.; Buras-Schnell, R.; Kylling, A.; Mayer, B.; Gasteiger, J.; Hamann, U.; Kylling, J.; Richter, B.; Pause, C.; Dowling, T.; et al. The libRadtran software package for radiative transfer calculations (version 2.0.1). Geosci. Model Dev. 2016, 9, 1647–1672. [Google Scholar] [CrossRef]
- Kurucz, R.L. High resolution irradiance spectrum 300 to 1000 nm, 2005. In Proceedings of the Air Force Research Laboratory Transmission Meeting, Lexington, MA, USA, 15–16 June 2005; Available online: http://kurucz.harvard.edu/sun/irradiance2005 (accessed on 6 April 2016).
- Anderson, G.P.; Clough, S.; Kneizys, F.; Chetwynd, J.; Shettle, E.P. AFGL Atmospheric Constituent Profiles (0.120 km); Technical Report, DTIC Document; Air Force Geophysics Laboratory, Hanscom Air Force Base: Hanscom AFB, MA, USA, 1986. [Google Scholar]
- Eriksson, P.; Buehler, S.; Davis, C.; Emde, C.; Lemke, O. ARTS, the atmospheric radiative transfer simulator, version 2. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 1551–1558. [Google Scholar] [CrossRef]
- Rothman, L.; Gordon, I.; Babikov, Y.; Barbe, A.; Benner, D.C.; Bernath, P.; Birk, M.; Bizzocchi, L.; Boudon, V.; Brown, L.; et al. The HITRAN2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 4–50. [Google Scholar] [CrossRef]
- Vandaele, A.C.; Hermans, C.; Fally, S.; Carleer, M.; Colin, R.; Mérienne, M.F.; Jenouvrier, A.; Coquart, B. High-resolution Fourier transform measurement of the NO2 visible and near-infrared absorption cross sections: Temperature and pressure effects. J. Geophys. Res. Atmos. 2002, 107, ACH 3–1–ACH 3–12. [Google Scholar] [CrossRef]
- Serdyuchenko, A.; Gorshelev, V.; Weber, M.; Chehade, W.; Burrows, J.P. High spectral resolution ozone absorption cross-sections—Part 2: Temperature dependence. Atmos. Meas. Tech. 2014, 7, 625–636. [Google Scholar] [CrossRef]
- Thalman, R.; Volkamer, R. Temperature dependent absorption cross-sections of O2-O2 collision pairs between 340 and 630 nm and at atmospherically relevant pressure. Phys. Chem. Chem. Phys. 2013, 15, 15371–15381. [Google Scholar] [CrossRef] [PubMed]
- Shettle, E.P. Models of aerosols, clouds, and precipitation for atmospheric propagation studies. In Atmospheric Propagation in the UV, Visible, IR, and MM-Wave Region and Related Systems Aspects, Proceedings of the ElectromagneticWave Propagation Panel Specialists’ Meeting, Copenhagen, Denmark, 9–13 October 1989; Advisory Group for Aerospace Research and Development (AGARD), NATO Military Committee: Neuilly sur Seine, France, 1990; Volume 1. [Google Scholar]
- Bodhaine, B.A.; Wood, N.B.; Dutton, E.G.; Slusser, J.R. On Rayleigh optical depth calculations. J. Atmos. Ocean. Technol. 1999, 16, 1854–1861. [Google Scholar] [CrossRef]
- Baldridge, A.; Hook, S.; Grove, C.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Liou, K.N. An Introduction to Atmospheric Radiation; Academic Press Ltd.: San Diego, CA, USA, 2002. [Google Scholar]
- Beirle, S.; Lampel, J.; Wagner, T. Proposal for a new parametrisation of the instrumental spectral response function in DOAS retrievals, 2015. In Proceedings of the 7th International DOAS Workshop, Brussel, Belgium, 6–8 July 2015.
- Frankenberg, C.; Platt, U.; Wagner, T. Iterative maximum a posteriori (IMAP)-DOAS for retrieval of strongly absorbing trace gases: Model studies for CH4 and CO2 retrieval from near infrared spectra of SCIAMACHY onboard ENVISAT. Atmos. Chem. Phys. 2005, 5, 9–22. [Google Scholar] [CrossRef]
- De Boor, C. A Practical Guide to Splines; Springer: New York, NY, USA, 2001. [Google Scholar]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific Publishing: Singapore, 2000. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Kuhlmann, G. flexDOAS Library. 2016. Available online: https://github.com/gkuhl/flexDOAS (accessed on 30 November 2016).
- Hueni, A.; Schlaepfer, D.; Jehle, M.; Schaepman, M. Impacts of dichroic prism coatings on radiometry of the airborne imaging spectrometer APEX. Appl. Opt. 2014, 53, 5344–5352. [Google Scholar] [CrossRef] [PubMed]
- Grainger, J.F.; Ring, J. Anomalous Fraunhofer line profiles. Nature 1962, 193, 762. [Google Scholar] [CrossRef]
- Hueni, A.; Biesemans, J.; Meuleman, K.; Dell’Endice, F.; Schlapfer, D.; Odermatt, D.; Kneubuehler, M.; Adriaensen, S.; Kempenaers, S.; Nieke, J.; et al. Structure, Components, and Interfaces of the Airborne Prism Experiment (APEX) processing and archiving facility. IEEE Trans. Geosci. Remote Sens. 2009, 47, 29–43. [Google Scholar] [CrossRef] [Green Version]
- Chance, K.V.; Spurr, R.J. Ring effect studies: Rayleigh scattering, including molecular parameters for rotational Raman scattering, and the Fraunhofer spectrum. Appl. Opt. 1997, 36, 5224–5230. [Google Scholar] [CrossRef] [PubMed]











| Characteristic | VNIR Channel | SWIR Channel |
|---|---|---|
| Spectral range | 372–1015 nm | 940–2540 nm |
| Spectral bands (mode) | 114 (binned), 334 (unbinned) | 198 (nominal) |
| Spectral sampling interval | 0.45–7.5 nm | 5.0–10.0 nm |
| Spectral resolution (FWHM) | 0.86–15.0 nm | 7.4–12.3 nm |
| Center wavelength accuracy | ≤0.2 nm for a single flight | |
| Spatial pixels (across track) | 1000 | |
| Field of view | 28.10 | |
| Instantaneous field of view | 0.028 | |
| Spatial resolution | 2.5 m at 5000 m above ground | |
| Signal to noise (SNR) | 625 (average over 50% reflecting target, Sun zenith: 24.4) | |
| Parameter | |
|---|---|
| Atmosphere | mid-latitude summer |
| Atmospheric absorber (near infrared) | , , , from HITRAN2012 [23] |
| Atmospheric absorber (visible) | [24], [25] and [26] |
| Atmospheric extinction | libRadtran default Rayleigh and Mie scattering, no Raman scattering |
| Solar reference spectrum | Kitt Peak Flux Atlas 2005 [20] |
| Solar zenith angle | 23 |
| Spectral range | 385–900 nm (0.001-nm resolution) |
| Surface elevation | 0 m |
| Surface reflectance | “asphalt paving”, “green grass” and “metal roofing” from ASTER |
| spectral library [29] | |
| Instrument altitude | 5000 m |
| Instrument viewing zenith angle | 0 (nadir) |
| Error Source | σ (mW·m·nm·sr) | Remark |
|---|---|---|
| APEX Instrument Error | ||
| single pixel | 1.31 | average instrument error |
| 200 binned pixels | 0.46 | assuming 70% random noise |
| 200 binned pixels | 0.09 | assuming 100% random noise |
| Forward Model Errors | ||
| Albedo parametrization (asphalt paving) | 0.038 | errors determined for the selected... |
| Albedo parametrization (green grass) | 0.174 | ...knot spacing in the forward... |
| Albedo parametrization (metal roofing) | 0.114 | ...model |
| Cross sections (, , ) | <0.006 | 5% error on the cross section |
| Reference optical depth (, ) | <0.030 | 5% error on reference optical depth |
| Ring effect (<450 nm) | <0.350 | standard deviation of the Ring spectrum... |
| Ring effect (>450 nm) | <0.050 | ...for a priori state vector |
| Solar reference spectrum | <0.004 and 0.040 | 0.1% and 1% uncertainty on data |
| Spline | Correlation Length (L) | ||
|---|---|---|---|
| Wavelength shift | 0.0 nm | 0.2 nm | 100 spectral pixels |
| Slit function | FWHM | 0.15 × FWHM | 100 spectral pixels |
| Offset | 0 mW·nm·m·sr | 5 mW·nm·m·sr | 1000 spectral pixels |
| Albedo | means and standard deviations of APEX surface reflectance dataset | ||
| Small Error: = 0.1 mW·m·nm·sr | Large Error: = 0.5 mW·m·nm·sr | ||||||
|---|---|---|---|---|---|---|---|
| λ(nm) | Shift (nm) | FWHM (%) | Offset () | Shift (nm) | FWHM (%) | Offset () | |
| 400 | 0.01 | 3.0 | 0.7 | 0.03 | 5.1 | 1.0 | |
| 450 | 0.03 | 4.3 | 0.9 | 0.06 | 6.8 | 1.4 | |
| (a) | 500 | 0.06 | 4.9 | 1.3 | 0.08 | 7.2 | 1.7 |
| 600 | 0.11 | 7.3 | 1.4 | 0.14 | 9.7 | 1.9 | |
| 760 | 0.08 | 4.3 | 0.9 | 0.13 | 7.1 | 1.7 | |
| 400 | 0.02 | 3.4 | 0.6 | 0.03 | 5.6 | 1.0 | |
| 450 | 0.04 | 5.0 | 0.9 | 0.06 | 7.4 | 1.4 | |
| (b) | 500 | 0.06 | 5.6 | 1.3 | 0.09 | 7.9 | 1.8 |
| 600 | 0.10 | 7.1 | 1.6 | 0.13 | 9.5 | 2.0 | |
| 760 | 0.02 | 1.3 | 1.5 | 0.05 | 2.4 | 2.1 | |
| 400 | 0.00 | 1.2 | 0.7 | 0.01 | 2.7 | 1.1 | |
| 450 | 0.01 | 1.4 | 1.0 | 0.02 | 3.3 | 1.5 | |
| (c) | 500 | 0.02 | 1.8 | 1.3 | 0.04 | 3.7 | 1.9 |
| 600 | 0.05 | 3.2 | 1.6 | 0.08 | 5.3 | 2.1 | |
| 760 | 0.02 | 1.0 | 1.5 | 0.05 | 2.2 | 2.2 | |
| surface reflectance: (a) “asphalt paving”, (b) “green grass” and (c) “metal roofing” | |||||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuhlmann, G.; Hueni, A.; Damm, A.; Brunner, D. An Algorithm for In-Flight Spectral Calibration of Imaging Spectrometers. Remote Sens. 2016, 8, 1017. https://doi.org/10.3390/rs8121017
Kuhlmann G, Hueni A, Damm A, Brunner D. An Algorithm for In-Flight Spectral Calibration of Imaging Spectrometers. Remote Sensing. 2016; 8(12):1017. https://doi.org/10.3390/rs8121017
Chicago/Turabian StyleKuhlmann, Gerrit, Andreas Hueni, Alexander Damm, and Dominik Brunner. 2016. "An Algorithm for In-Flight Spectral Calibration of Imaging Spectrometers" Remote Sensing 8, no. 12: 1017. https://doi.org/10.3390/rs8121017
APA StyleKuhlmann, G., Hueni, A., Damm, A., & Brunner, D. (2016). An Algorithm for In-Flight Spectral Calibration of Imaging Spectrometers. Remote Sensing, 8(12), 1017. https://doi.org/10.3390/rs8121017