Wind Resource Assessment for High-Rise BIWT Using RS-NWP-CFD
Abstract
:1. Introduction
2. Analysis Methods
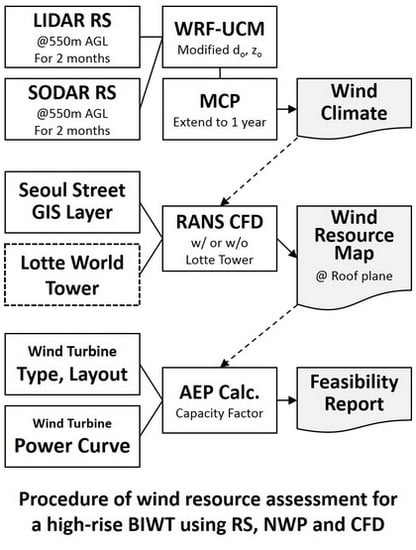
2.1. Analysis Procedure
2.2. Remote Sensing Campaign
2.3. Numerical Weather Prediction
2.4. Computational Fluid Dynamics
3. Analysis Results
3.1. Remote Sensing Campaign
3.2. Numerical Weather Prediction
3.3. Long-Term Correction
- Mean wind speed = 4.9 m/s;
- Wind power density = 160 W/m2 (wind class 1, poor);
- Weibull distribution scale factor c = 5.5 m/s, shape factor k = 1.72; and
- Prevailing wind direction WNW.
3.4. Computational Fluid Dynamics
3.5. Energy Production Calcuations
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AEP | Annual Energy Production |
| BAWT | Building-Augmented Wind Turbine |
| BIWT | Building-Integrated Wind Turbine |
| CFD | Computational Fluid Dynamics |
| DRR | Data Recovery Rate |
| MCP | Measure-Correlate-Predict |
| NWP | Numerical Weather Prediction |
| RANS | Reynolds-Averaged Navier-Stokes |
| RS | Remote Sensing |
| WRF | Weather Research Forecasting |
| UCM | Urban Canopy Model |
References
- Rouse, R. The Pyramids of Egypt. 2016. Available online: https://public.tableau.com/en-us/s/gallery/pyramids-egypt (accessed on 12 December 2016).
- Ken, B. Sustainable Architecture and Simulation Modelling; Dublin Institute of Technology: Dublin, Ireland, 2001. [Google Scholar]
- Doerr Architecture. Definition of Sustainability and the Impacts of Buildings. 2003. Available online: http://www.doerr.org/services/sustainability.html (accessed on 12 December 2016).
- Smith, R.F.; Killa, S. Bahrain World Trade Center (BWTC): The first large-scale integration of wind turbines in a building. Struct. Des. Tall Spec. Build. 2007, 16, 429–439. [Google Scholar] [CrossRef]
- Cochran, B.C.; Damiani, R.R. Integrating Wind Energy into the Design of Tall Buildings—A Case Study of the Houston Discovery Tower. In Proceedings of the American Wind Energy Association’s WINDPOWER 2008 Conference & Exhibition, Houston, TX, USA, 1–4 June 2008.
- Li, Q.S.; Shu, Z.R.; Chen, F.B. Performance assessment of tall building-integrated wind turbines for power generation. Appl. Energy 2016, 165, 777–788. [Google Scholar] [CrossRef]
- Stuart, A.; Mark, W. Strata SE1, London, UK: The First In-House Wind Generator. Struct. Eng. Int. 2011, 21, 37–40. [Google Scholar]
- Chen, F.; Kusaka, H.; Bornstein, R.L.; Ching, J.; Grimmond, C.S.B.; Grossman-Clarke, S.; Loridan, T.; Manning, K.W.; Martilli, A.; Miao, S.; et al. The integrated WRF/urban modelling system: Development, evaluation, and applications to urban environmental problems. Int. J. Climatol. 2011, 31, 273–288. [Google Scholar] [CrossRef]
- Macdonald, R.W.; Griffiths, R.F.; Hall, D.J. An improved method for estimation of surface roughness of obstacle arrays. Atmos. Environ. 1998, 32, 1857–1864. [Google Scholar] [CrossRef]
- Kato, M.; Launder, B.E. The modeling of turbulence flow around stationary and vibrating square cylinders. In Proceedings of the 9th Symposium on Turbulence Shear Flows, Kyoto, Japan, 16–18 August 1993.
- Lien, F.S.; Yee, E.; Cheng, Y. Simulation of mean flow and turbulence over a 2D building array using high-resolution CFD and a distributed drag force approach. J. Wind Eng. Ind. Aerodyn. 2004, 92, 117–158. [Google Scholar] [CrossRef]
- Gryning, S.E.; Floors, R.R.; Peña, A.; Batchvarova, E.; Brümmer, B. Weibull wind-speed distribution parameters derived from a combination of wind-lidar and tall-mast measurements over land, coastal and marine sites. Bound. Layer Meteorol. 2016, 159, 329–348. [Google Scholar] [CrossRef] [Green Version]
- Rogers, A.L.; Rogers, J.W.; Manwell, J.F. Comparison of the performance of four measure-correlate-predict algorithms. J. Wind Eng. Ind. Aerodyn. 2005, 93, 243–264. [Google Scholar] [CrossRef]
- Kim, J.S.; Kim, H.G.; Park, H.D. Surface wind regionalization based on similarity of time-series wind vectors. Asian J. Atmos. Environ. 2016, 10, 80–89. [Google Scholar] [CrossRef]
- Korea Institute of Energy Research. Korea New and Renewable Energy Resource Atlas, 2nd ed.; Ministry of Science, ICT and Future Planning, New and Renewable Energy Resource Center: Daejeon, Korea, 2015; Available online: http://www.kier-solar.org/pdf/getFile.do?type=WIND (accessed on 12 December 2016).






















| Wind Turbine GWE-10KH | Square Cone Case | Circular Cone Case | ||
|---|---|---|---|---|
| AEP (MWh) | Capacity Factor | AEP (MWh) | Capacity Factor | |
| WT#1 | 2.81 | 3.21% | 3.01 | 3.44% |
| WT#2 | 3.14 | 3.58% | 3.43 | 3.91% |
| WT#3 | 3.28 | 3.74% | 5.09 | 5.81% |
| TW#4 | 2.18 | 2.49% | 3.09 | 3.53% |
| Overall | 11.4 | 3.26% | 14.6 | 4.18% |
| Wind Turbine Excel-S | Square Cone Case | Circular Cone Case | ||
|---|---|---|---|---|
| AEP (MWh) | Capacity Factor | AEP (MWh) | Capacity Factor | |
| WT#1 | 4.53 | 5.17% | 4.89 | 5.47% |
| WT#2 | 4.63 | 5.28% | 5.12 | 4.84% |
| WT#3 | 4.98 | 5.68% | 7.67 | 8.76% |
| TW#4 | 3.59 | 4.10% | 4.77 | 5.45% |
| Overall | 17.7 | 5.06% | 22.4 | 6.38% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.-G.; Jeon, W.-H.; Kim, D.-H. Wind Resource Assessment for High-Rise BIWT Using RS-NWP-CFD. Remote Sens. 2016, 8, 1019. https://doi.org/10.3390/rs8121019
Kim H-G, Jeon W-H, Kim D-H. Wind Resource Assessment for High-Rise BIWT Using RS-NWP-CFD. Remote Sensing. 2016; 8(12):1019. https://doi.org/10.3390/rs8121019
Chicago/Turabian StyleKim, Hyun-Goo, Wan-Ho Jeon, and Dong-Hyeok Kim. 2016. "Wind Resource Assessment for High-Rise BIWT Using RS-NWP-CFD" Remote Sensing 8, no. 12: 1019. https://doi.org/10.3390/rs8121019
APA StyleKim, H. -G., Jeon, W. -H., & Kim, D. -H. (2016). Wind Resource Assessment for High-Rise BIWT Using RS-NWP-CFD. Remote Sensing, 8(12), 1019. https://doi.org/10.3390/rs8121019