Wind Turbine Wake Characterization from Temporally Disjunct 3-D Measurements

Abstract

Scanning LiDARs can be used to obtain three-dimensional wind measurements in and beyond the atmospheric surface layer. In this work, metrics characterizing wind turbine wakes are derived from LiDAR observations and from large-eddy simulation (LES) data, which are used to recreate the LiDAR scanning geometry. The metrics are calculated for two-dimensional planes in the vertical and cross-stream directions at discrete distances downstream of a turbine under single-wake conditions. The simulation data are used to estimate the uncertainty when mean wake characteristics are quantified from scanning LiDAR measurements, which are temporally disjunct due to the time that the instrument takes to probe a large volume of air. Based on LES output, we determine that wind speeds sampled with the synthetic LiDAR are within 10% of the actual mean values and that the disjunct nature of the scan does not compromise the spatial variation of wind speeds within the planes. We propose scanning geometry density and coverage indices, which quantify the spatial distribution of the sampled points in the area of interest and are valuable to design LiDAR measurement campaigns for wake characterization. We find that scanning geometry coverage is important for estimates of the wake center, orientation and length scales, while density is more important when seeking to characterize the velocity deficit distribution.

1. Introduction

In order to improve the efficiency of wind farms, it is necessary to maximize their overall power production and to minimize the fatigue loads experienced by each turbine. This in turn relies on a quantitative understanding of the flow that meets each wind turbine and its interaction with the tower and rotor. Wind turbines are increasingly deployed in large-scale arrays. The upwind turbines experience undisturbed (i.e., free stream) conditions, where turbulence is determined by atmospheric stability and topographic characteristics. As they extract energy from the wind, turbines also disturb the flow that moves through them generating a wake [1]. As a result, the turbines downstream are subjected to flows with lower mean kinetic energy and higher turbulent kinetic energy. These complex flows are expensive to measure and model with sufficient accuracy. Integrating measurements and models offers the potential to advance quantitative analyses of wake characteristics and atmospheric flows to determine optimal wind farm layout and enable efficient wind turbine control strategies.

Remote sensing tools, such as LiDARs, are advantageous for wind energy applications (e.g., resource assessment and wake characterization) because of their ability to sample beyond hub heights at relatively high spatial and temporal resolution and without modifying the flow. Two major distinctions in wind LiDAR technology are between continuous wave (cw) and pulsed systems and between their scanning capabilities. While some LiDARs scan exclusively conically using the velocity azimuth display (VAD) technique, others are also capable of range height indicator (RHI, also known as elevation) and plan position indicator (PPI, also referred to as sector or azimuth) scans [2,3], both of which have been used for wind turbine wake measurements (e.g., [2,4,5]). Conically scanning cw LiDARs have been used most frequently for one-dimensional wake analyses to quantify the resulting power losses and wake-induced fatigue either scanning from the ground, when they sample vertical wind profiles at a fixed spatial location [6], or nacelle-mounted, where they can be used to obtain wind profiles through the turbine axis at hub height either downstream for wake research [7,8] and turbulent dissipation studies [9] or upstream for wind turbine control [10]. Currently, new technologies are being developed that allow for more flexible scanning geometries [2,11], thus broadening the application range of such systems [12] and exploiting the measuring potential of multiple LiDAR arrays [13]. While cw LiDARs can sample at very short ranges, they are typically limited to distances <200 m because the effective probe volume increases to the fourth power of the focus range [14], thus increasing the uncertainty in the wind speed measurements away from the instrument [15].

Conversely, pulsed scanning LiDAR like the one used in this study are able to sample large three-dimensional (3D) volumes of the atmosphere by achieving ranges $\mathcal{O}({10}^2-{10}^4)$ m and measuring at several pre-determined azimuth and elevation angles. They can also measure wakes from the ground [4] or can be mounted on the turbine nacelle [8]. The sampling duration of one 3D scan increases linearly with the number of azimuth and elevation angles sampled because it takes time for the instrument to retrieve robust statistics of the Doppler shift at several range gates and to mechanically reposition the transmitter before emitting the next beam. At the cost of sampling a large number of points, the time interval between two beams is ∼2 s for the measurements used in the present study. The dwell time of the instrument is ∼1 s (higher than some other studies, e.g., 0.2 s in [16]), and the additional time is spent in processing the return signal and relocating the scanner. This instrument time combined with the large number of beams required to sample a large volume results in measurements that represent neither a snapshot of the atmosphere nor a mean field. They are instead a set of instantaneous observations sampled at different times and locations. When such measurements are used to characterize the unsteady, inhomogeneous flows in wind turbine wakes, it is important to have a measure of the uncertainty in the retrieved data that considers the instrument limitations, the scanning geometry characteristics and the assumptions being made for data retrieval and analysis. While previous work has quantified LiDAR-derived radial velocity uncertainty and proposed means to reduce it (e.g., [17]), the present work is unique in that it focuses on wind turbine wake characterization metrics.

The notion of combining LiDAR and models to improve processing techniques and understand uncertainty propagation has been around for over a decade [18]. As LiDAR use becomes more widespread and computational resources develop, this approach is gaining popularity. Recently, studies have started to combine high-fidelity large-eddy simulation (LES) and LiDAR to investigate near wake physics [19] and quantify errors prior to conducting measurement campaigns [20]. The first part of the work presented here utilizes this approach to estimate the differences between wake measurements obtained with a scanning pulsed LiDAR, the true snapshot of the same volume and the true temporal mean over the time it takes to complete a full 3D scan. The analysis is conducted by placing an imaginary scanning LiDAR in an LES to obtain scans that are equivalent in time and space to measurements collected during a field campaign. The differences serve as an estimate of the uncertainty when temporally-disjunct point measurements are assumed to be representative of mean conditions. The disjunct points, the instantaneous fields and the true means are then used to characterize the wake, and differences in the wake metrics are obtained to further quantify uncertainty in wake characterization from LiDAR observations. We focus on a single ground-based instrument and present wake characterization metrics that can be used when resources are limited and multiple or nacelle-mounted units are impractical.

The second part of this work seeks to identify and characterize single-wake conditions measured with a pulsed scanning LiDAR during a 22-h period with a fixed scanning geometry. The wake metrics considered include wake center, length scales, orientation and velocity deficit ($vd$) statistics and are defined for transverse-vertical planes at discrete distances downstream of the wake-generating turbine following the methodology proposed in [21]. A significant challenge is the time-varying wind direction and rotor yaw, which dictate the angle between the fixed scanned volume and the vertical planes. We quantify this effect by proposing scanning geometry indices that describe the measurement coverage and density on a vertical plane given an area of interest and an optimal spatial resolution between the sampled points. The field measurements and simulations are described in Section 2, and the results given in Section 3. Recommendations for defining the scanning geometry prior to measurement collection and for characterizing mean wakes from temporally disjunct point measurements are proposed along with a final discussion in Section 4.

2. Materials and Methods

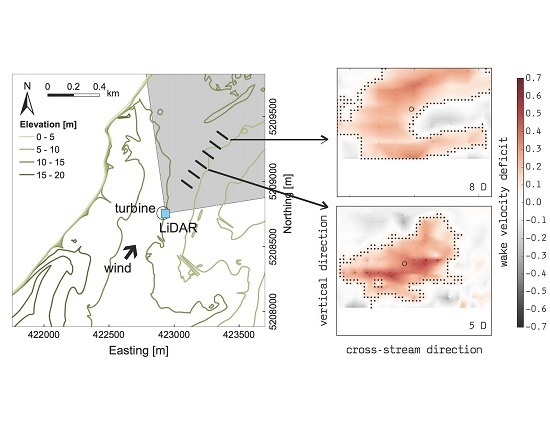
2.1. Field Scans

The observational dataset used in this work was collected during the Prince Edward Island Wind Energy Experiment at the Wind Energy Institute of Canada [22]. We focus on single wake measurements during a 22-h period (26 May 2015 13:00 UTC–27 May 2015 11:00 UTC) downstream of a 2-MW DeWind D9.2 turbine with a hub height ($z_H$, the H subscript indicates turbine hub throughout the manuscript) of 80 m and a rotor diameter (D) of 93 m. The wake characterization is based on the metrics proposed by [21], which are defined for two-dimensional planes of data in the cross-stream (x) and vertical (z) directions. This framework allows for an analysis of the wake expansion and deformation with downstream distance, which are directly related to wake recovery and to the loads experienced by downstream turbines. Vertical planes are typically obtained with ground-based LiDAR using RHI scans, in which the azimuth angle (θ) is kept constant and the elevation angle ($\varphi$) is varied. However, in the present work, the mean flow direction (y) is perpendicular to the plane of interest ($xz$), precluding the use of RHI scans. Stacked sector scans must be used instead, which are obtained by varying θ at multiple $\varphi s$.

The sector scans in this work were obtained using a Galion LiDAR, which has a wavelength of 1.5 $\mathsf{\mu }$m and a pulse repetition frequency of 15 kHz. Throughout the manuscript, the terms “stacked (sector) scans” and “3D scan” are used interchangeably when referring to the volume probed by all of the θ and $\varphi$ beams. The scanning geometry was constant for the entire measurement period and can be visualized in Figure 1. A total of $N_{\theta }=46$ azimuth angles were configured in the interval $\theta \in \left\{[{351}^{°},{360}^{°}]\bigcup [0^{°},{81}^{°}]\right\}$, and their position relative to the site and the turbine is given in Figure 2, which also shows the location of a meteorological mast with a Gill sonic anemometer measuring at a frequency of 10 Hz at a height of 60 m. The azimuth angles follow the meteorological convention where $\theta =0^{°}$ points north. The elevation angles were $\varphi \in [3^{°},{19}^{°}]$ for a total of $N_{\varphi }=8$ elevation beams, and $\varphi =0^{°}$ is aligned with the approximately flat ground (Figure 2). Each radial velocity measurement is defined by the coordinates $(\theta ,\varphi ,r)$ where r is the radial distance from the instrument along the laser beam, with a relatively high resolution range gate size of 30 m (as compared to >100 m in [2,16], 72 m in [3] and 18 m in [4]). During this period, 111 3D scans were obtained. The method used to derive vertical planes of data from the 3D scan is outlined below.

• Data are filtered by range gate number (G), signal-to-noise ratio ($SNR$) and radial velocity magnitude ($U_r$). The criteria are:

  $$\begin{array}{c}2\le G\le 45\\ 0.01(-20\mathrm{dB})<SNR\le 10\left(10\mathrm{dB}\right)\\ U_r<30{\mathrm{m}\mathrm{s}}^{-1}\end{array}$$

  and therefore, the total possible number of radial velocity measurements within a stack of scans is $44\times 46\times 8$ (number of gates $\times N_{\theta }\times N_{\varphi }$). The first range gate is discarded as it is in the LiDAR blind zone. The $SNR$ lower limit is recommended by the manufacturer, and the upper limit (also used in previous studies [16]) is enough to filter out hard targets and cloud water for our dataset. The upper limit in the radial velocities is an arbitrary value higher than any of the observed values during the measurement period (e.g., Figure 1) and serves to filter out unrealistic measurements and erroneous logging.
• The location vector in Cartesian coordinates in a fixed frame of reference for each point is obtained as:

  $$\overrightarrow{d_F}=(x_F,y_F,z_F)=(r\cos \varphi \sin \theta ,r\cos \varphi \cos \theta ,r\sin \varphi )$$

  where $x_F$ ($y_F$) is positive in the east (north) direction. All quantities in the fixed frame are subscripted with F.
• For each 3D scanned volume, the highest elevation sector scan ($\varphi ={19}^{°}$) is selected to determine the mean wind direction $\langle \beta \rangle$ (angled brackets refer to values averaged over the entire 3D scan). Within this scan, all points sampled at least 0.25 D above the rotor are considered, which includes five range gates. An estimate of the horizontal wind components $u_F$ and $v_F$ is obtained for each range gate within this sector scan sub-sample by solving the linear system:

  $$\left[\begin{array}{cc}\cos {19}^{°}\sin {\theta }_1& \cos {19}^{°}\cos {\theta }_1\\ ⋮& ⋮\\ \cos {19}^{°}\sin {\theta }_{46}& \cos {19}^{°}\cos {\theta }_{46}\end{array}\right]\left[\begin{array}{c}{u}_F\\ v_F\end{array}\right]=\left[\begin{array}{c}{U}_{r_1}\\ ⋮\\ U_{r_{46}}\end{array}\right]$$

  (1)

  using a least-squares approach, where ($u_F,v_F$) are the wind components along the directions ($x_F,y_F$) and $U_{r_i}$ are the radial velocity measurements along an arc of constant G for an azimuth angle ${\theta }_i$. The vertical component $w_F$ is assumed to be negligible, consistent with previous studies (e.g., [23]). The validity of this assumption was verified with sonic anemometer data (not shown) and is based on the physical understanding that the magnitude of vertical velocities is much lower than that of horizontal velocities and that the mean magnitude of w is close to zero when averaged over periods of ∼10 min, which is approximately the time the LiDAR took to complete a full stack of sector scans. As suggested in [4], multiple LiDARs must be considered when seeking to investigate all components of the wind field within wakes.
  The values of ($u_F,v_F$) are then averaged across the five range gates within the sub-sample to yield the mean wind direction estimate $\langle \beta \rangle$ for the scanned volume. The robustness of this method for the present experiment is reflected in the time series shown in Figure 3, where the minimum and maximum $\langle \beta \rangle$ estimates for each 3D scan are compared with sonic anemometer measurements and the turbine nacelle position. The LiDAR estimates follow the sonic values more closely than the turbine data, indicating that the assumptions of low veer and negligible vertical velocity are acceptable for the atmospheric conditions observed during the experiment.
• Assuming a constant mean wind direction $\langle \beta \rangle$ for each 3D scan, the horizontal wind speed at each point $U_F(x_F,y_F,z_F)$ is estimated from the radial velocity $U_r$ as:

  $$U_F=-\frac{U_r}{\cos \varphi \cos \mathrm{\Delta }\theta }$$

  (2)

  where $\mathrm{\Delta }\theta =\langle \beta \rangle -\theta$ is the scan offset, defined as the angle between the scan wind direction and the laser beam azimuthal direction. Orthogonal scans are filtered out following the LiDAR manufacturer recommendation to remove points for which the laser beam makes an angle between ${70}^{°}$ and ${110}^{°}$ with the mean wind direction (∼1.4% of the measurements).
• All points in the scan are rotated so that the coordinate system is aligned with the mean wind direction. Throughout the manuscript, the quantities in this streamwise frame of reference are given without the F subscript as: $\overrightarrow{U}=(u,v)$, $\overrightarrow{d}=(x,y)$ where x and y are the cross-stream and streamwise directions, respectively.
• Vertical planes of data are obtained at a given distance downstream of the turbine by selecting all of the sampled points whose streamwise coordinate y falls within the desired distance plus or minus some specified buffer $\mathrm{\Delta }y$, taken to be the range gate width of 30 m. In this analysis, the scanning LiDAR was deployed at the base of the turbine (Figure 2), and we apply an assumption of no yaw error. Therefore, the analysis only considers 3D scans for which the LiDAR-estimated $\langle \beta \rangle$ is within ${15}^{°}$ of the turbine nacelle position, resulting in 80 sector scan stacks. The value of ${15}^{°}$ was chosen as a threshold because while it is small (half of the wind industry standard ${30}^{°}$ sectors when performing azimuthal analyses), it still allows for an offset between the turbine and the nacelle, which is necessary given the uncertainties inherent in both datasets (e.g., inaccuracies in the wind direction estimate from the LiDAR and in the recorded nacelle position) and the potential presence of yaw misalignment. As indicated by the sonic time series (Figure 3), the large differences between the LiDAR and the nacelle datasets reflect not an inability of the LiDAR to estimate the wind direction, but rather the necessarily delayed response of the nacelle to wind direction changes or high uncertainty in the turbine measurements.
• In order to quantify the potential contribution of each vertical slice to wind turbine wake characterization, it is important to consider how much of the area of interest is covered by the sampled points and how dense this coverage is. To do that, we define two indices. The first one is the scanning geometry coverage ($SGC$), which is calculated as:

  $$SGC=\frac{A}{A_{ref}}$$

  (3)

  where A is the area covered by the scanned points within the total reference area $A_{ref}$, which extends 1 D to either side of the hub in the horizontal and vertical directions being only limited by the presence of the ground. Within the covered area A, the scanning geometry density ($SGD$) is defined as:

  $$SGD=\frac{n}{n_{ref}(\mathrm{\Delta }x,\mathrm{\Delta }z)}$$

  (4)

  where n is the number of points in the covered area A relative to a reference value $n_{ref}$, which is the maximum number of points that could cover the same area A given a desired fixed spatial resolution $\mathrm{\Delta }x$ and $\mathrm{\Delta }z$, which for the present study is set to 5 m.

The scanning geometry coverage and density vary with downstream distance and with wind direction (Figure 4), which dictates the turbine yaw and, therefore, the angle of the $xz$-plane relative to the fixed scanned volume. The scanning geometry θ angles are fixed for the period considered and were determined at the start of the day based on the forecast wind direction. The optimal wind direction ${\beta }_{opt}$ is defined as the wind direction that yields the best coverage of points for a given scanning geometry. For the period considered in this study, ${\beta }_{opt}={216}^{°}$ and aligns with the center of the scanning arc at $\theta ={36}^{°}$, which is the symmetry point around which the sector scan stacks return ample coverage in the horizontal direction. It is convenient to define the direction offset $\mathrm{\Delta }\beta =\langle \beta \rangle -{\beta }_{opt}$ as the difference between the actual wind direction during a scan and the optimal value for that given scanning geometry. For the present setup, the coverage is lowest for westerly winds when half of the $xz$-planes are outside of the scan (Figure 2). The $SGD$ values do not approach unity because of the high $n_{ref}$ value used in its definition. Similarly, $SGC$ < 0.9 for the present scanning geometry since the θ and $\varphi$ angles were chosen to maximize the retrievals at several distances downstream rather than focusing on obtaining complete coverage within a narrow range in the streamwise direction.

2.2. Synthetic Scans

The uncertainty in the measurements and resulting wake characterization is estimated by placing an imaginary scanning LiDAR at the bottom of a wind turbine in an LES of a single wake under slightly stable conditions, which is also true of the measurements [22]. From here onwards, the term “synthetic scan” is used to refer to data that are obtained by sampling numerical simulation output according to the spatial and temporal coordinates of each point in the $xz$-planes obtained from the field measurements. The LES dataset is obtained with the National Renewable Energy Laboratory’s (NREL) Simulator For Wind Farm Applications (SOWFA) [24] using the Lagrangian-averaged dynamic Smagorinsky model [25]. The turbines are modeled as rotating actuator lines [26]. The lower boundary is a flat rough wall with the roughness length representative of offshore conditions, and the top surface is a zero-stress impenetrable lid 1 km above the surface. The offshore simulation is assumed to be a good approximation to the field experiment site, which is narrow (∼${10}^3$ m in width), approximately flat (Figure 2) and surrounded by ocean [22].

The spatial resolution of the simulation mesh is 10 m away from the turbine and 1–2 m around the turbines and in the wake. The turbine has a 77-m rotor diameter and an 80-m hub height. A precursor LES of the atmospheric boundary layer is initially run without turbines in order to generate the necessary initial and boundary conditions for the wind turbine simulation, and the resulting inflow has a hub height turbulence intensity of ∼4% and a mean wind speed of ∼6.5 m·${\mathrm{s}}^{-1}$. The lateral boundary conditions are periodic, and the simulation is driven by a pressure gradient force that allows the hub height mean wind speed and direction to approach a desired value. The data are saved in $xz$-planes at discrete distances downstream of the turbine at a frequency of 1 Hz for a 12-min period. The effect of the weighting function relative to the temporal lag across points is assumed to be small when sampling the synthetic scans, since the focus of the current study is to assess the impact of the temporal and spatial resolution of the sampled points on wake characterization metrics.

As described in Section 2.1, each 3D scan obtained in the field is characterized by a different mean wind direction $\langle \beta \rangle$ and therefore has a different coverage and density of points in the $xz$-planes being analyzed. The method employed in this work to obtain the synthetic scans from LES data accounts for this dynamic behavior of the sampled points and for the instrument dwell time. The same 12-min LES dataset is resampled for the appropriate points each time that the field LiDAR starts a new 3D scan. Therefore, the synthetically-scanned points are equivalent to the field scans spatially and temporally. The LES data are denoted with the subscript L and the temporally disjunct synthetic scans with the over-ring symbol: $({\mathring{u}}_L,{\mathring{v}}_L)$. It takes the instrument ∼2 s to sample radial velocities along one combination of θ and $\varphi$. For the 46 azimuth and 8 elevation angles considered, a full scan takes ∼12 min, and the sampled values do not represent instantaneous nor mean fields. The difference between the sampled points and the true 12-min mean or instantaneous fields can be estimated by using the LES data. Throughout the manuscript, true instantaneous fields are denoted by ($u_L,v_L$) and are sampled at the first second of the scan. Temporal means over the time it takes to complete a full 3D scan are obtained from 1-Hz data and denoted by the overbar (${\overline{u}}_L,{\overline{v}}_L$).

2.3. Wake Identification

From this point onwards, the methodology applied to the field and synthetic wakes is the same except when noted. The first step towards wake characterization is to distinguish free stream from wake points. The scanned points at each vertical slice are interpolated onto a regular grid with a spatial resolution of 5 m, and the $vd$ is calculated for each plane as:

$$vd(x,z)=1-\frac{U(x,z)}{U_{\infty }\left(z\right)}$$

(5)

where $U=\sqrt{u^2+v^2}$ is the horizontal wind speed downstream of the turbine and retrieved from the scan (whether the points are temporally disjunct depends on the case being analyzed), and $U_{\infty }=\sqrt{u_{\infty }^2+v_{\infty }^2}$ is the free stream wind speed. During the 22-h period considered, no free stream measurements were performed in the field. Therefore, the free stream profile must be estimated from measurements downstream of the turbine $U_{\infty }\left(z\right)\approx U_{\infty ,down}\left(z\right)$. On each $xz$-plane, the profile that is furthest away from the turbine hub in the cross-stream direction is assumed to be representative of free stream conditions:

$$U_{\infty ,down}\left(z\right)=U(x_{max},z)$$

(6)

To avoid sampling a profile that is in the wake when data coverage is limited, we constrain the minimum acceptable distance away from the hub as half the rotor diameter plus an expansion factor based on the Jensen model [27]:

$$x_{max}>0.5+ky$$

(7)

where y is the downstream distance in units of D and k the wake decay coefficient, taken to be 0.05 as traditionally used for offshore conditions as the default parameter in the WAsPPark model [28]. The sensitivity of this parameter to atmospheric stability is beyond the scope of the present study, and the adopted value is consistent with recommendations from previous studies [28,29]. For the synthetic scans exclusively, available upstream data are used as an additional measure of the free stream where $U_{\infty }\left(z\right)\approx U_{\infty ,up}(x_H,z)$.

The points with a $vd$ value above a minimum threshold are flagged as wake points. To determine this threshold, a Gaussian function is fit to the horizontal $vd$ profile at hub height, as has been done in previous LiDAR wake characterization studies [30,31]. The 95% confidence interval of the Gaussian ($2\sigma$) is then used to determine the threshold $vd$ value to mark the wake edges for a particular $xz$-plane. The horizontal direction is chosen here because the scanning geometry covers a greater range in azimuth than in elevation (which misses the upper part of the wake closer to the turbine) and because the free stream wind in homogeneous terrain is expected to vary less in the horizontal than in the vertical direction.

2.4. Wake Characterization

For each 3D scan, the wakes are sampled at discrete distances downstream of the turbine and characterized regarding their center, height, width, orientation and $vd$ statistics. A schematic of the quantities evaluated is given in Figure 5 for the coordinate system adopted. The wake area identification is described in Section 2.3. The wake center is given as the center of gravity of the $vd$ distribution within the wake area [21,32]. The height and width are the distances from edge to edge of the wake in the vertical and horizontal directions, through the wake center. The orientation is estimated by defining an ellipse with the same second-order moments as the wake shape and calculating the angle between its major axis and the vertical axis in the clockwise direction looking downstream. The yaw error is assumed to be negligible and is justified by limiting the difference between the nacelle position and the LiDAR-estimated wind direction to ${15}^{°}$ in the field measurements (see Section 2.1).

3. Results

3.1. Difference between Scan, Mean and Snapshot

This subsection quantifies how the wind speed retrieved from each scanned value (${\mathring{U}}_L$) compares to both the mean (${\overline{U}}_L$) and instantaneous ($U_L$) values for the synthetic scans obtained from an LES. This serves as an estimate of the level of uncertainty when large volumes of wind turbine wake data probed by a pulsed scanning LiDAR are assumed to be representative of mean or instantaneous conditions.

For each 12-min stack of sector scans obtained in the field, three spatially-equivalent synthetic scans are obtained from LES data by resampling the same 12-min LES time series according to the wind direction offset $\mathrm{\Delta }\beta$ for ${\mathring{U}}_L$, ${\overline{U}}_L$ and $U_L$. The LES planes are stored at a 1-Hz frequency. To obtain the mean wind speed ${\overline{U}}_L$, each point in a $xz$-plane is sampled every second for the duration of the scan and then averaged over time. The instantaneous fields refer to snapshots at the first second of the scan. The comparisons here focus on the wind speed and are evaluated separately for each 3D scan. First, the mean pointwise difference in each $xz$-plane is quantified by the normalized root-mean-squared (rms) differences:

$${\mathrm{\Delta }}_{rms}={\left\{\frac{1}{N}\sum {\left[\frac{\left({\mathring{U}}_L-U_{ref}\right)}{{\mathring{U}}_L}\times 100\right]}^2\right\}}^{1/2}$$

(8)

where ${\mathring{U}}_L$ are the temporally-disjunct points sampled by the instrument in the LES, $U_{ref}$ either the mean or the instantaneous value at the same point (also from the LES) and N the total number of points in the $xz$-plane, which varies as a function of $\mathrm{\Delta }\beta$. After obtaining one ${\mathrm{\Delta }}_{rms}$ value for each downstream distance within each 3D scan, these values are averaged over time to give an overall measure of the differences. The results are given in

Table 1. Normalized rms differences ${\mathrm{\Delta }}_{rms}$ (%) between synthetic scan wind speeds ${\mathring{U}}_L$, the instantaneous values at the first second of the scan $U_L$ and the mean over the time it takes to complete the scan ${\overline{U}}_L$. Averages are over 80 3D scans, chosen to mimic the observations.

	3 D	4 D	5 D	6 D	7 D	8 D
${\mathring{U}}_L$ and $U_L$	13.2	13.2	13.5	12.3	11.5	9.9
${\mathring{U}}_L$ and ${\overline{U}}_L$	9.9	9.7	8.5	8.7	8.0	7.6

and indicate that the temporally-disjunct synthetic scan deviates from both the mean and the instantaneous values by similar magnitudes, but is closer (within $10\%$) to the mean. This is a reasonable result because measurements are collected along a single beam at a time, so to obtain better agreement between instantaneous and measured values, one would need to perform the analysis along the laser beam or in the downstream direction, instead of cross-stream, as is the case of interest. Overall, the differences decrease with downstream distance as the wake recovers, and the variability in the wind field decreases. These results indicate that a high density of scanned points (found exclusively closer to the turbine, as shown in Figure 4) is not required to investigate mean wind turbine wake characteristics.

It is also important to assess how the spatial variation in the retrieved wind speeds compares to the one seen in the mean and instantaneous fields. This was done in two ways; first, by calculating the turbulence intensity ($TI=\sigma /\overline{U}$ where σ is the standard deviation and $\overline{U}$ the mean) for each downstream plane in each stack. The temporal mean of the $TI$ values is close to ∼20% for all distances downstream regardless of whether the scan, mean or instantaneous fields are considered, indicating that overall, the instrument scan time does not compromise the spatial variability retrieved in the wind speed measurements. This can further be examined by considering the wind speed profiles in the vertical (Figure 6a) and horizontal (Figure 6b) directions from the mean and instantaneous LES values and from the synthetic scans. In this case, the mean and instantaneous profiles are obtained by using the LES $xz$-planes without limiting the data to the points that a particular scan would sample at some $\mathrm{\Delta }\beta$. The scan profiles at each distance downstream are obtained by linearly interpolating between the synthetically-scanned points onto a line passing through the turbine hub in either direction and then calculating the temporal mean and standard deviation of all such profiles. Because the scanning geometry considered has a wider coverage in the azimuthal direction than in the vertical, the ${\mathring{U}}_L$ profiles in Figure 6b are complete between $x=\pm 1$ D, while the vertical profiles in Figure 6a sample the entire rotor plane (between $z=\pm 0.5$ D) from 4 D–7 D. The profiles in Figure 6 are given in m·${\mathrm{s}}^{-1}$ to focus on the synthetic instrument ability to reconstruct the velocity field regardless of the method used to estimate the free stream and therefore derive the $vd$, which is a diagnostic variable. The analysis indicates that the reconstructed profiles follow the mean profiles closely, reproduce the double Gaussian in the near wake and capture the wake recovery. Note that our analysis isolates the effect of disjunct-in-time data. In reality, the line-of-sight averaging of the measurements constitute an additional source of error that likely smooths steep gradients in the observations, as has been found for vertical profiling LiDARs [20], but has not yet been quantified for scanning LiDARs.

3.2. Difference between Wake Characteristics from Scan, Mean and Snapshot

As previously mentioned, the ultimate objective of this work is to use the temporally-disjunct radial velocity retrievals to characterize the 12-min mean wake in the field scans. Before that is done, this section presents an estimate of the uncertainty level in wake characterization for the given scanning geometry and wake characterization metrics. The LES wakes are identified and characterized three times: using synthetic scans with temporally-disjunct, instantaneous and 12-min mean data points. A comparison between these three gives a valuable first indication of the uncertainty level in the synthetic scan that mimics the field data, while keeping in mind that the magnitudes may differ under different turbulence intensities and atmospheric stability conditions [33].

The 80 3D synthetic scans considered in this analysis are equivalent to those remaining in the observational dataset after quality control. They differ only in wind direction, and the same 12-min time series of LES data is resampled each time that a new scan begins, to account for the dynamic wind direction offset $\mathrm{\Delta }\beta$. As mentioned in Section 2.3, it is necessary to define a free stream profile in order to characterize the wake. Planes that are not wide enough to provide such an estimate are not included in the analysis when downstream data are used to estimate free stream conditions. In total, 61 3D scans are left when $U_{\infty }\approx U_{\infty ,down}$ and 69 when $U_{\infty }\approx U_{\infty ,up}$.

For each stack, the wake is identified and characterized according to the sampled (${\mathring{U}}_L$, $U_L$ and ${\overline{U}}_L$) values following the description in Section 2.3 and Section 2.4. The uncertainty in these metrics is quantified by absolute differences $\left|\mathrm{\Delta }\right|=\left|\mathring{x}-x_{ref}\right|$, where $\mathring{x}$ are the metrics derived from the temporally-disjunct synthetically-scanned points and $x_{ref}$ the wake metrics from the temporal mean or the instantaneous scans. For width, height and the $vd$ statistics, these differences are normalized relative to the scanned value $\mathring{x}$. For the wake center, they are not normalized and are instead given as a vector sum of the differences in both the horizontal and vertical directions in units of D. For wake orientation, absolute differences are given in units of degrees.

An illustrative example of the uncertainty in wake characterization is described here for the case shown in Figure 7. In this example, the lowest $SGC$ is ∼47% at a downwind distance of 3 D and the highest ∼74% at 7 D. The lowest $SGD$ is ∼9% at 8 D and the highest ∼55% at 3 D. This pattern is typical for a LiDAR operated at the turbine base since a very high elevation angle would be needed to capture the near wake across the entire rotor. The mean wake center location for this 3D scan is well characterized by the ${\mathring{U}}_L$ values, with the smallest $\left|\mathrm{\Delta }\right|$ (i.e., difference between the location identified using the 12-min mean LES output and that conditionally sampled to mimic the LiDAR) being ∼0.05 D at 8 D. The maximum wake center $\left|\mathrm{\Delta }\right|$ is ∼0.2 D in the near wake (at 3 D) where the $SGC$ is low and a large area of the wake is not covered. As illustrated in Figure 7, these errors are within the differences between the instantaneous and mean wake center. The wake width was also reasonably estimated for the slices with higher coverage and density, with $\left|\mathrm{\Delta }\right|$ below ∼12% except at 7 and 8 D, where the wake area estimated from the LES synthetic scans greatly exceeds that from the full LES output. Because the scanning geometry is less restricted in azimuth than in elevation angles, the limitations in coverage are reflected in the vertical distribution of points and affect the estimates of wake height for which the errors ranged between $7\%$ and $52\%$ for the example in Figure 7. Because of the approximate symmetry of the 12-min mean wake about its center, $SGD$ is more important than $SGC$ when attempting to estimate the statistics of the $vd$ distribution. The differences for mean $vd$ increased with downstream distance, but no clear conclusion can be drawn from the standard deviation of the $vd$. The linearly-interpolated slices also gave a good estimate of the wake orientation for this case, with $\left|\mathrm{\Delta }\right|$ lower than $5^{°}$ except at 3 D, where the wake area itself is not well approximated.

Analyzing a single case provides intuition into the magnitudes of differences in each of the wake metrics considered. However, to obtain an overall understanding of the uncertainties, it is useful to consider the ensemble mean of the error values in the synthetic scans, which are shown in Figure 8 relative to the mean and instantaneous fields using the two methods of estimating the free stream profile as described in Section 2.3. First, consider the difference between the metrics obtained from the temporally-disjunct points and from the mean fields (Figure 8, black markers). For wake center, orientation and height, the largest errors are seen at 3 D where the area of interest (centered at the hub) is only partially covered by the scanning geometry. As for the example above, the wake center and orientation errors are small for the other downstream distances. This is similar to findings from previous work that evaluated the errors resulting from assumptions made while processing wake measurements from profiling LiDARs [20]. The wake height is poorly estimated all throughout, likely due to shortcomings in the definition of wake height and the method used to estimate it, which is very sensitive to differences in the wake orientation. As expected, errors in the $vd$ mean and standard deviation are inversely proportional to the density of retrieved points, and therefore, the lowest error values are seen from 3–6 D. It is also evident from Figure 8 that in some cases, the results are very sensitive to the method used to estimate the free stream, emphasizing the importance of including periodic free stream measurements in the scanning geometry when seeking to characterize wakes in field experiments. Finally, Figure 8 also shows that the synthetic scan wake metrics are closer to the mean than to the instantaneous estimates, which was also seen for the pointwise analysis performed in Section 3.1.

3.3. Field Wakes’ Characterization

After testing the metrics on synthetic scans, they can be used to identify and characterize wind turbine wakes in field measurements. An example of $xz$-planes from measurements is given in Figure 9, where $\mathrm{\Delta }\beta$ is the same as in the LES wakes of Figure 7. Note that despite representing the same scan, there is a small discrepancy in the coverage and density indices between the field wakes and the synthetic wakes, which arises from the limited extent in the LES data planes. It is evident and expected that the field measurements exhibit a higher level of complexity than the LES. Some of the reasons include: the effect of roughness, terrain and obstacles; the small-scale turbulent structures that result from the interaction of the flow with the rotor and tower; the intricacies of ambient atmospheric conditions where a complex interplay of stability and surface characteristics act to modify the flow; random errors from the instrument and wind speed retrieval algorithms; and assumptions inherent in the method and described in Section 2.

Keeping in mind the uncertainty levels estimated in Section 3.2 and the added complexity of the field measurements, the temporal means of wake metrics considering 59 3D scans in the 22-h period considered are given in

Table 2. Mean wake characteristics obtained from the field measurements and including 59 3D scans. The wake center is given as a vector in the cross-stream ($\widehat{x}$) and vertical directions ($\widehat{z}$) for a coordinate system centered at the turbine hub.

	Unit	3 D	4 D	5 D	6 D	7 D	8 D
center	D$\widehat{x}$, D$\widehat{z}$	0.13, 0.08	0.18, 0.12	0.16, 0.16	0.15, 0.20	0.10, 0.25	0.08, 0.18
orientation	°	15	4	15	16	25	6
height	D	0.8	1.0	1.0	1.0	1.0	0.9
width	D	1.5	1.4	1.3	1.5	1.4	1.6
$vd$ mean	-	0.22	0.19	0.15	0.13	0.12	0.11
$vd$ SD	-	0.11	0.10	0.08	0.07	0.06	0.06

. As previously determined (Section 3.2), it is possible to use these data to get robust estimates of the wake area and center for distances where there is reasonable wake coverage and density. For the current scanning geometry, this translates to downstream distances between 4 and 7 D. These methods can therefore be used to estimate the mean wake trajectory driven by changes in wind direction that happen over the LiDAR sampling time. Estimates of the wake center movement are shown in Figure 10 for the period when enough measurements are available for this range of distances. Here, the mean wake trajectory refers to motion of the wake center in the time scale of the scanning duration (∼12 min here) and is analogous to large-scale wake meandering. With the exception of a few cases, the estimates are stable across all downstream distances. The vertical trajectory is mostly positive and <0.5 D, indicating a wake centered above the turbine hub, consistent with streamline analysis of flow over the escarpment [22,34] and with the upward wake deflection often resulting from tilt-up of the rotor shaft found in previous studies [30,31]. Its magnitude tends to increase with downstream distance from the turbine. Conversely, the magnitudes of the wake center motion in the horizontal direction are similar throughout the distances considered (but not over time) and reach magnitudes of up to ∼0.8 D. The values are predominantly negative indicating a wake center that is on average to the left of the hub when looking downstream along the streamwise (y) coordinate. This consistent wake deflection could be a systematic bias in the method resulting from neglecting veer across the rotor, which in some conditions (especially under stable stratification [35]) has been shown to be an important parameter resulting in wake steering and wake skew. The outliers in Figure 10 do not represent a particularly large value of $\mathrm{\Delta }\beta$ nor very low coverage and density. It is therefore likely related to the assumptions made to retrieve the horizontal wind speeds, which must be considered carefully in less stable situations where the vertical velocity component cannot be neglected.

As seen with the LES data, the wake width and height are more difficult to estimate, and the values obtained from field measurements do not indicate clear wake expansion with downstream distance (Table 2), possibly due to small expansion under stable stratification. Robust estimates of length scales and wake orientation rely on both the coverage and density of points in the sampled transects, which is difficult to obtain for several downstream distances with a single ground-based LiDAR. If these metrics are of primary interest, these considerations must be taken into account when designing the scanning geometry for an experiment. The estimates of $vd$ statistics clearly show wake recovery away from the turbine. The mean values are given in Figure 11 and follow the similarity prediction at infinite Reynolds numbers where $vd\propto y^{-2/3}$ [36] despite the large variation in the 22-h period considered (as quantified by the standard deviation and shown in Figure 11). The theoretical curve prefactor in Figure 11 was obtained by fitting the expected power law to the data and is slightly lower than the value estimated in [31] when considering several previously-published studies of wake recovery. This difference is likely due to the short period considered, where atmospheric conditions are predominantly stable [22]. The standard deviation values, which represent the spatial variation of the $vd$ in the $xz$-planes also match the expected results and decrease as the wake recovers (Table 2).

4. Conclusions

The objectives of this work are multi-fold: first, to estimate the difference between spatially- and temporally-disjunct wind speed measurements sampled by a ground-based pulsed LiDAR, an instantaneous snapshot of the flow and the temporal means over the time it takes to complete the 3D scan; second, to quantify how these differences affect wake characterization; finally, to apply wake characterization metrics [21] to LiDAR measurements. To our knowledge, this is the first work to provide a quantitative estimate of the uncertainty arising from these temporal limitations inherent in LiDAR measurements when large atmospheric volumes are probed. A simulated scanning LiDAR within an LES is used as the basis for this analysis, and we additionally provide a detailed methodology to derive cross-stream planes of wind turbine wakes at several distances downstream from a stack of sector scans.

All of the analyses are based on transverse-vertical planes of horizontal wind at discrete distances downstream of a turbine and under single-wake conditions. Based on LES output, we determine that wind speeds sampled with the synthetic LiDAR are within ∼10% of the actual mean values and that the disjunct nature of the scan does not compromise the spatial variation of wind speed within the planes. The sampled points deviate more from the instantaneous values closer to the turbine, with rms differences ∼13% when averaged over 80 sector scan stacks. Based on the LES synthetic scans, we show the scanning geometry coverage is very important to characterization of the wake center, orientation and length scales. Because of the radial symmetry in the mean $vd$ field, ample coverage of points is not required to obtain good estimates of the $vd$ mean and standard deviation for which scanning geometry density is more important.

When the wake characterization metrics are applied to 59 3D scans obtained with a pulsed scanning LiDAR during a field experiment, the methods produce a consistent estimate of the wake center starting at 4 D, and the estimates for vertical and horizontal wake trajectory are robust between 4 and 7 D. Due to the scanning geometry limitations for this experiment, the wake length scales (i.e., width and height) are not well diagnosed and do not show a clear expansion with downstream distance. The characterization metrics can be applied to estimate the mean and standard deviation of the $vd$ and, therefore, to quantify wake recovery. The consideration of the proposed indices to quantify scanning geometry density and coverage is recommended when planning a measurement campaign with a scanning LiDAR with the objective of characterizing wind turbine wakes. Limiting the number of range gates and ensuring a good coverage of points in the vertical and horizontal directions is important to estimate wake length scales. Alternatively, higher density retrievals are necessary to estimate $vd$ statistics. When focusing on the wake center, a compromise between coverage and density can be reached, and measurements can be made at a higher temporal frequency with a lower number of retrieved points. Finally, we recommend including periodic free stream measurements in the scanning geometry in order to minimize the uncertainty in $vd$ quantification.