Estimation of Land Surface Temperature through Blending MODIS and AMSR-E Data with the Bayesian Maximum Entropy Method
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area

2.2. Data
2.2.1. Satellite-Derived LST Products
| MODIS LST | AMSR-E LST | |
|---|---|---|
| Time range | From 1 August 2010 to 28 July 2011 | |
| Temporal resolution | Daily (1:30 A.M. local time) | |
| Space range | 91.5°E–92.5°E, 31°N–32°N | |
| Spatial resolution | Approx. 1 km | Approx. 25 km |
| Projection | Sinusoidal | Albers Conical Equal Area |
2.2.2. Data Used in This Study

| The Nth Period (Date) | MODIS LST Availability | AMSR-E LST Availability | |
|---|---|---|---|
| Period 1 | 34 (from 27 June to 6 July, 2011) | 25.2% | 76.3% |
| Period 2 | 23 (from 9 March to 18 March, 2011) | 32.4% | 87.5% |
| Period 3 | 17 (from 8 January to 17 January, 2011) | 47.5% | 86.3% |
| Period 4 | 04 (from 31 August to 9 September, 2010) | 57.6% | 95.6% |
| Period 5 | 07 (from 30 September to 9 October, 2010) | 73.7% | 85.6% |
| Period 6 | 14 (from 9 December to 18 December, 2010) | 83.6% | 85.0% |
| Period 7 | 11 (from 9 November to 18 November, 2010) | 91.4% | 95.0% |
2.2.3. Comparison Data
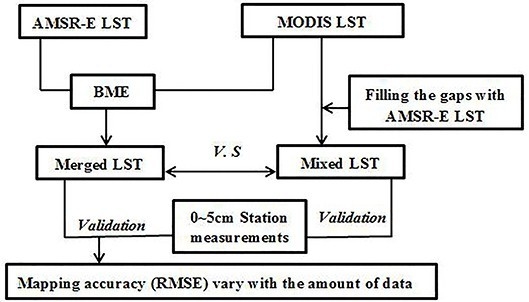
3. Methodology

3.1. Spatiotemporal Random Field
3.2. BME Method

A. Step 1
B. Step 2
C. Step 3
4. Results
4.1. Modeling the Spatial Covariance Models

| No. | Exponential (s)/Spherical (t) | Spherical (s)/Exponential (t) | ||||
|---|---|---|---|---|---|---|
| Period 1 | 0.4 | 0.18 | 4 | 0.6 | 0.6 | 12 |
| Period 2 | 0.4 | 0.20 | 4 | 0.6 | 0.5 | 20 |
| Period 3 | 0.4 | 0.40 | 4 | 0.6 | 0.6 | 25 |
| Period 4 | 0.4 | 0.20 | 3 | 0.6 | 0.5 | 20 |
| Period 5 | 0.4 | 0.25 | 4 | 0.6 | 0.6 | 25 |
| Period 6 | 0.4 | 0.30 | 5 | 0.6 | 0.6 | 40 |
| Period 7 | 0.4 | 0.20 | 5 | 0.6 | 0.6 | 40 |
4.2. Availability and Spatial Distribution of the MODIS LSTs, AMSR-E LSTs, and Merged LSTs
| No | MODIS LST | AMSR-E LST | Merged LST |
|---|---|---|---|
| Period 1 | 25.2% | 76.3% | 100% |
| Period 2 | 32.4% | 87.5% | 100% |
| Period 3 | 47.5% | 86.3% | 100% |
| Period 4 | 57.6% | 95.6% | 100% |
| Period 5 | 73.7% | 85.6% | 100% |
| Period 6 | 83.6% | 85.0% | 100% |
| Period 7 | 91.4% | 95.0% | 100% |

4.3. Comparison of Merged LSTs with the 0–5 cm Soil Temperature

4.4. Validation of Merged LSTs with the Adjusted Station Measurements


| Period | Period 1 | Period 2 | Period 3 | Period 4 | Period 5 | Period 6 | Period 7 |
|---|---|---|---|---|---|---|---|
| Availability of MODIS LSTs | 25.2% | 32.4% | 47.5% | 57.6% | 73.7% | 83.6% | 91.4% |
| Availability of AMSR-E LSTs | 76.3% | 87.5% | 86.3% | 95.6% | 85.6% | 85.0% | 95.0% |
| RMSE | 4.53 °C | 4.07 °C | 4.26 °C | 3.56 °C | 3.10 °C | 3.08 °C | 2.31 °C |
4.5. Comparison of the Differences between BME Merged LSTs and Mixed LSTs

5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Prihodko, L.; Goward, S.N. Estimation of air temperature from remotely sensed surface observations. Remote Sens. Environ. 1997, 60, 335–346. [Google Scholar] [CrossRef]
- Solomon, S.; Qin, D.; Manning, M.; Chen, Z.; Marquis, M.; Averyt, K.B.; Tignor, M.; Miller, H.L. Climate Change 2007: The Physical Science Basis; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; Volume 6. [Google Scholar]
- Vogt, J.V.; Viau, A.A.; Paquet, F. Mapping regional air temperature fields using satellite-derived surface skin temperatures. Int. J. Climatol. 1997, 17, 1559–1579. [Google Scholar] [CrossRef]
- Jia, Y.Y.; Li, Z.L. Progress in land surface temperature retrieval from passive microwave remotely sensed data. Prog. Geogr. 2006, 25, 96–105. [Google Scholar]
- Zhou, J.; Chen, Y.H.; Wang, J.F.; Zhan, W.F. Maximum nighttime urban heat island (UHI) intensity simulation by integrating remotely sensed data and meteorological observations. IEEE J. Sel. Top. Appl. Earth Observ. 2011, 4, 138–146. [Google Scholar] [CrossRef]
- Marquı́nez, J.; Lastra, J.; Garcı́a, P. Estimation models for precipitation in mountainous regions: The use of GIS and multivariate analysis. J. Hydrol. 2003, 270, 1–11. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.Z.; Yan, G.J.; Wan, Z.M.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Lakshmi, V.; Czajkowski, K.; Dubayah, R.; Susskind, J. Land surface air temperature mapping using TOVS and AVHRR. Int. J. Remote Sens. 2001, 22, 643–662. [Google Scholar] [CrossRef]
- Aumann, H.H.; Chahine, M.T.; Gautier, C.; Goldberg, M.D.; Kalnay, E.; McMillin, L.M.; Revercomb, H.; Rosenkranz, P.W.; Smith, W.L.; Staelin, D.H.; et al. AIRS/AMSU/HSB on the Aqua mission: Design, science objectives, data products, and processing systems. IEEE Trans. Geosci. Remote Sens. 2003, 41, 253–264. [Google Scholar] [CrossRef]
- Zhou, J.; Li, J.; Zhang, L.X. Intercomparison of methods for estimating land surface temperature from a Landsat-5 TM image in an arid region with low water vapour in the atmosphere. Int. J. Remote Sens. 2012, 33, 2582–2602. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I.; Nørgaard, A.; Fensholt, R.; Eklundh, L. Estimation of diurnal air temperature using MSG SEVIRI data in West Africa. Remote Sens. Environ. 2007, 110, 262–274. [Google Scholar] [CrossRef]
- Vancutsem, C.; Ceccato, P.; Dinku, T.; Connor, S.J. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
- Jang, J.D.; Viau, A.A.; Anctil, F. Neural network estimation of air temperatures from AVHRR data. Int. J. Remote Sens. 2004, 25, 4541–4554. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, Y.; Cheng, M.; Jiang, H. Near-surface air temperature retrieval from Chinese Geostationary FengYun Meteorological Satellite (FY-2C) data. Int. J. Remote Sens. 2014, 35, 3892–3914. [Google Scholar] [CrossRef]
- Dash, P.; Göttsche, F.M.; Olesen, F.S.; Fischer, H. Land surface temperature and emissivity estimation from passive sensor data: Theory and practice—Current trends. Int. J. Remote Sens. 2002, 23, 2563–2594. [Google Scholar] [CrossRef]
- Wan, Z.M.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Gillespie, A.T.; Rokugawa, S.; Hook, S. Temperature emissivity separation from Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Qin, Z.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel–Egypt border region. Int. J. Remote Sens. 2001, 22, 3719–3746. [Google Scholar] [CrossRef]
- Zhou, J.; Li, J.; Zhao, X.; Zhan, W.F.; Guo, J.X. A modified single channel algorithm for land surface temperature retrieval from HJ-1B satellite data. J. Infrared Millim. Waves 2011, 30, 61–67. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.L. Towards a local split window method over land surfaces. Int. J. Remote Sens. 1990, 11, 369–393. [Google Scholar] [CrossRef]
- Owe, M.; Van de Griend, A.A. On the relationship between thermodynamic surface temperature and high-frequency (37 GHz) vertically polarized bright-ness temperature under semi-arid conditions. Int. J. Remote Sens. 2001, 22, 3521–3532. [Google Scholar] [CrossRef]
- Mcfarland, M.J.; Miller, R.L.; Neale, C.M.U. Land surface temperature derived from the SSM/I passive microwave brightness temperatures. IEEE Trans. Geosci. Remote Sens. 1990, 28, 839–845. [Google Scholar] [CrossRef]
- Holmes, T.R.H.; de Jeu, R.A.M.; Owe, M.; Dolman, A.J. Land surface temperature from Ka band (37 GHz) passive microwave observations. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Royer, A.; Poirier, S. Surface temperature spatial and temporal variations in North America from homogenized satellite SMMR-SSM/I microwave measurements and reanalysis for 1979–2008. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Surdyk, S. Using microwave brightness temperature to detect short-term surface air temperature changes in Antarctica: An analytical approach. Remote Sens. Environ. 2002, 80, 256–271. [Google Scholar] [CrossRef]
- Basist, A.; Grody, N.C.; Peterson, T.C. Using the Special Sensor Microwave/Imager to monitor land surface temperatures, wetness, and snow cover. J. Appl. Meteorol. 1998, 37, 888–911. [Google Scholar] [CrossRef]
- Seemann, S.W.; Borbas, E.E.; Li, J.; Menzel, W.P.; Gumley, L.E. MODIS Atmospheric Profile Retrieval Algorithm Theoretical Basis Document; NASA: Greenbelt, MD, USA, 2006. [Google Scholar]
- Jones, L.A.; Ferguson, C.R.; Kimball, J.S.; Zhang, K.; Chan, S.T.K.; McDonald, K.C.; Njoku, E.G.; Wood, E.F. Satellite microwave remote sensing of daily land surface air temperature minima and maxima from AMSR-E. IEEE J. Sel. Top. Appl. Earth Obser. Remote Sens. 2010, 3, 111–123. [Google Scholar] [CrossRef]
- Chen, S.S.; Chen, X.Z.; Chen, W.Q. A simple retrieval method of land surface temperature from AMSR-E passive microwave data—A case study over Southern China during the strong snow disaster of 2008. Int. J. Appl. Earth Observ. Geoinf. 2011, 13, 140–151. [Google Scholar] [CrossRef]
- Bisht, G.; Venturini, V.; Islam, S.; Jiang, L. Estimation of the net radiation using MODIS (moderate resolution imaging spectroradiometer) data for clear sky days. Remote Sens. Environ. 2005, 97, 52–67. [Google Scholar] [CrossRef]
- Batra, N.; Islam, S.; Venturini, V.; Bisht, G.; Jiang, L. Estimation and comparison of evapotranspiration from MODIS and AVHRR sensors for clear sky days over the Southern Great Plains. Remote Sens. Environ. 2006, 103, 1–15. [Google Scholar] [CrossRef]
- Zhou, J.; Dai, F.; Zhang, X.; Zhao, S.; Li, M. Developing a temporally land cover-based look-up table (TL-LUT) method for estimating land surface temperature based on AMSR-E data over the Chinese landmass. Int. J. Appl. Earth Observ. Geoinf. 2015, 34, 35–50. [Google Scholar] [CrossRef]
- Hachem, S.; Allard, M.; Duguay, C. Using the MODIS land surface temperature product for mapping permafrost: An application to Northern Quebec and Labrador, Canada. Permafr. Periglac. Processes 2009, 20, 407–416. [Google Scholar] [CrossRef]
- Ran, Y.H.; Li, X.; Jin, R. Estimation of the mean annual surface temperature and surface frost number using the MODIS land surface temperature products for mapping permafrost in China. In Proceedings of the Tenth International Conference on Permafrost (TICOP), Salekhard, Russia, 25–29 June 2012; pp. 317–321.
- Ryu, Y.; Baldocchi, D.D.; Kobayashi, H.; Ingen, C.; Li, J.; Black, T.A.; Beringer, J.; Gorsel, E.; Knohl, A.; Law, B.E. Integration of MODIS land and atmosphere products with a coupled process model to estimate gross primary productivity and evapotranspiration from 1 km to global scales. Glob. Biogeochem. Cycle 2011, 25, GB4017. [Google Scholar] [CrossRef]
- Bisht, G.; Bras, R.L. Estimation of net radiation from the MODIS data under all sky conditions: Southern Great Plains case study. Remote Sens. Environ. 2010, 114, 1522–1534. [Google Scholar] [CrossRef]
- Jang, K.; Kang, S.; Lim, Y.; Jeong, S.; Kim, J.; Kimball, J.S.; Hong, S.Y. Monitoring daily evapotranspiration in Northeast Asia using MODIS and a regional Land Data Assimilation System. J. Geophys. Res. Atmos. 2013, 118, 927–940. [Google Scholar] [CrossRef]
- Jang, K.; Kang, S.; Kimball, J.S.; Hong, S.Y. Retrievals of all-weather daily air temperature using MODIS and AMSR-E data. Remote Sens. 2014, 6, 8387–8404. [Google Scholar] [CrossRef]
- Christakos, G. Modern Spatiotemporal Geostatistics; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Christakos, G.; Serre, M.L. BME analysis of spatiotemporal particulate matter distributions in North Carolina. Atmos. Environ. 2000, 34, 3393–3406. [Google Scholar] [CrossRef]
- Bogaert, P.; Christakos, G.; Jerrett, M.; Yu, H.L. Spatiotemporal modelling of ozone distribution in the State of California. Atmos. Environ. 2009, 43, 2471–2480. [Google Scholar] [CrossRef]
- Christakos, G.; Kolovos, A.; Serre, M.L.; Vukovich, F. Total ozone mapping by integrating databases from remote sensing instruments and empirical models. IEEE Trans. Geosci. Remote Sens. 2004, 42, 991–1008. [Google Scholar] [CrossRef]
- D’Or, D.; Bogaert, P.; Christakos, G. Application of the BME approach to soil texture mapping. Stoch. Environ. Res. Risk Assess. 2001, 15, 87–100. [Google Scholar] [CrossRef]
- Douaik, A.; van Meirvenne, M.; Tóth, T. Statistical methods for evaluating soil salinity spatial and temporal variability. Soil Sci. Soc. Am. J. 2007, 71, 1629–1635. [Google Scholar] [CrossRef]
- Lee, S.J.; Balling, R.; Gober, P. Bayesian maximum entropy mapping and the soft data problem in urban climate research. Ann. Assoc. Am. Geogr. 2008, 98, 309–322. [Google Scholar] [CrossRef]
- Li, A.; Bo, Y.; Zhu, Y.; Guo, P.; Bi, J.; He, Y. Blending multi-resolution satellite sea surface temperature (SST) products using Bayesian maximum entropy method. Remote Sens. Environ. 2013, 135, 52–63. [Google Scholar] [CrossRef]
- Wu, G.; Liu, Y.; Zhang, Q.; Duan, A.; Wang, T.; Wan, R.; Liu, X.; Li, W.; Wang, Z.; Liang, X. The influence of mechanical and thermal forcing by the Tibetan Plateau on Asian climate. J. Hydrometeorol. 2007, 8, 770–789. [Google Scholar] [CrossRef]
- Yang, K.; Guo, X.; He, J.; Qin, J.; Koike, T. On the climatology and trend of the atmospheric heat source over the Tibetan Plateau: An experiments-supported revisit. J. Clim. 2011, 24, 1525–1541. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the MODIS land-surface temperature/emissivity products. Remote Sens. Environ. 2008, 112, 59–74. [Google Scholar] [CrossRef]
- Yang, K.; Qin, J.; Zhao, L.; Chen, Y.Y.; Tang, W.; Han, M.; Chen, Z.; Lv, N.; Ding, B.; Wu, H.; et al. A multi-scale soil moisture and freeze-thaw monitoring network on the third pole. Bull. Am. Meteorol. Soc. 2013, 94, 1907–1916. [Google Scholar] [CrossRef]
- Christakos, G. Random Field Models in Earth Sciences; Academic Press: San Diego, CA, USA, 1992. [Google Scholar]
- Spadavecchia, L.; Williams, M. Can spatio-temporal geostatistical methods improve high resolution regionalisation of meteorological variables? Agric. For. Meteorol. 2009, 149, 1105–1117. [Google Scholar] [CrossRef]
- Olea, R.A. Normalization. In Geostatistics for Engineers and Earth Scientists; Springer Science+Business Media: New York, NY, USA, 1999; pp. 31–38. [Google Scholar]
- Bolles, R.C.; Fischler, M.A. A RANSAC-based approach to model fitting and its application to finding cylinders in range data. IJCAI 1981, 1981, 637–643. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kou, X.; Jiang, L.; Bo, Y.; Yan, S.; Chai, L. Estimation of Land Surface Temperature through Blending MODIS and AMSR-E Data with the Bayesian Maximum Entropy Method. Remote Sens. 2016, 8, 105. https://doi.org/10.3390/rs8020105
Kou X, Jiang L, Bo Y, Yan S, Chai L. Estimation of Land Surface Temperature through Blending MODIS and AMSR-E Data with the Bayesian Maximum Entropy Method. Remote Sensing. 2016; 8(2):105. https://doi.org/10.3390/rs8020105
Chicago/Turabian StyleKou, Xiaokang, Lingmei Jiang, Yanchen Bo, Shuang Yan, and Linna Chai. 2016. "Estimation of Land Surface Temperature through Blending MODIS and AMSR-E Data with the Bayesian Maximum Entropy Method" Remote Sensing 8, no. 2: 105. https://doi.org/10.3390/rs8020105
APA StyleKou, X., Jiang, L., Bo, Y., Yan, S., & Chai, L. (2016). Estimation of Land Surface Temperature through Blending MODIS and AMSR-E Data with the Bayesian Maximum Entropy Method. Remote Sensing, 8(2), 105. https://doi.org/10.3390/rs8020105