L-Band Polarimetric Target Decomposition of Mangroves of the Rufiji Delta, Tanzania
Abstract
:1. Introduction
2. Study Area and Data

2.1. Characteristics of Rufiji Mangrove Species

2.2. Satellite Imagery
3. Methods
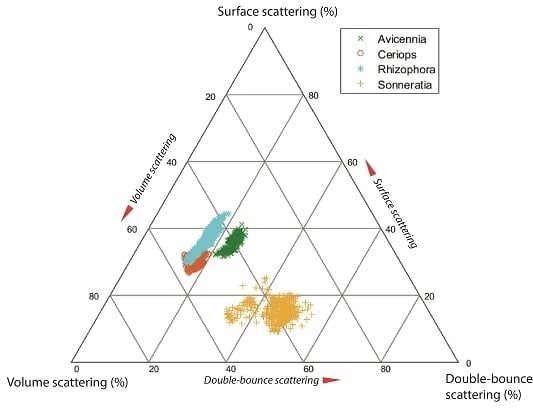
4. Results and Discussion
4.1. Entropy-Anisotropy-Alpha

4.2. Incoherent Target Decompositions

4.3. Differences in Scattering Mechanism between Mangrove Species

4.4. Temporal Variations
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bryceson, I.; Massinga, A. Coastal resources and management systems influenced by conflict and migration: Mecufi, Mozambique. Ambio 2002, 31, 512–517. [Google Scholar] [CrossRef] [PubMed]
- Masalu, D.C.P. Challenges of coastal area management in coast developing countries- lessons from the proposed Rufiji delta prawn farming project, Tanzania. Ocean Coast. Manag. 2003, 46, 175–188. [Google Scholar] [CrossRef]
- Burgess, N.D.; Mwakalila, S.; Munishi, P.; Pfeifer, M.; Willcock, S.; Shirima, D.; Hamidu, S.; Bulenga, G.B.; Rubens, J.; Machano, H.; et al. REDD herrings or REDD menace: Response to Beymer-Farris and Basset. Glob. Environ. Chang. 2013, 23, 1349–1354. [Google Scholar] [CrossRef]
- Semesi, A. Management Plan for the Mangrove Ecosystem of Mainland Tanzania; Ministry of Tourism, Natural Resources and Environment, Forestry and Beekeeping Division: Dar es Salaam, Tanzania, 1991; Volume 1–10. [Google Scholar]
- Erftemeijer, P.; Hamerlynck, O. Die-back of the mangrove Heritiera littoralis dryland, in the Rufiji Delta (Tanzania) following El Niño floods. J. Coast. Res. 2005, 42, 228–235. [Google Scholar]
- Hoppe-Speer, S.C.L.; Adams, J.B.; Rajkaran, A.; Bailey, D. The response of the red mangrove Rhizophora mucronata Lam. to salinity and inundation in South Africa. Aquat. Bot. 2011, 95, 71–76. [Google Scholar] [CrossRef]
- Mangora, M. Poverty and institutional management standoff: A restoration and conservation dilemma for mangrove forests of Tanzania. In Proceedings of the 18th Commonwealth Forestry Conference, Edinburgh, UK, 28 June–2 July 2010.
- Heumann, B.W. Satellite remote sensing of mangrove forests: Recent advances and future opportunities. Prog. Phys. Geogr. 2011, 35, 87–108. [Google Scholar] [CrossRef]
- Kuenzer, C.; Bluemel, A.; Gebhardt, S.; Quoc, T.V.; Dech, S. Remote sensing of mangrove ecosystems: A review. Remote Sens. 2011, 3, 878–928. [Google Scholar] [CrossRef]
- Rauste, Y.; Hame, T.; Pullianen, J.; Heiska, K.; Hallikainen, M. Radar-based forest biomass estimation. Int. J. Remote Sens. 1994, 15, 2797–2808. [Google Scholar] [CrossRef]
- Lucas, R.M.; Mitchell, A.L.; Rosenqvist, Å.; Proisy, C.; Melius, A.; Ticehurst, C. The potential of L-band SAR for quantifying mangrove characteristics and change: Case studies from the tropics. Aquat. Conserv. Mar. Freshw. Ecosyst. 2007, 17, 245–264. [Google Scholar] [CrossRef]
- Mermoz, S.; Réjou-Méchain, M.; Villard, L.; Le Toan, T.; Rossi, V.; Gourlet-Fleury, S. Decrease of L-band backscatter with biomass of dense forests. Remote Sens. Environ. 2015, 159, 307–317. [Google Scholar] [CrossRef]
- Cornforth, W.A.; Fatoyinbo, T.E.; Freemantle, T.P.; Pettorelli, N. Advanced Land Observing Satellite Phased Array type L-band SAR (ALOS PALSAR) to inform the conservation of mangroves: Sundarbans as a case study. Remote Sens. 2013, 5, 224–237. [Google Scholar] [CrossRef]
- Wang, Y.; Imhoff, M.L. Simulated and observed L-HH radar backscatter from tropical mangrove forests. Int. J. Remote Sens. 1993, 14, 2819–2828. [Google Scholar] [CrossRef]
- Proisy, C.; Mougin, E.; Fromard, F.; Trichon, V.; Karam, M.A. Interpretation of polarimetric radar signatures of mangrove forests. Remote Sens. Environ. 2000, 71, 56–66. [Google Scholar] [CrossRef]
- Clewley, D.; Lucas, R.; Accad, A.; Armston, J.; Bowen, M.; Dwyer, J.; Pollock, S.; Bunting, P.; Eyre, T.; Kelly, A.; et al. An approach to mapping forest growth stages in Queensland, Australia through integration of ALOS PALSAR and Landsat sensor data. Remote Sens. 2012, 4, 2236–2255. [Google Scholar] [CrossRef] [Green Version]
- Neumann, M.; Saatchi, S.; Ulander, L.M.H.; Fransson, J.E.S. Assessing performance of L- and P-band polarimetric interferometric SAR data in estimating boreal forest above-ground biomass. IEEE Trans. Geosci. Remote Sens. 2012, 50, 714–726. [Google Scholar] [CrossRef]
- Freeman, A. Fitting a two-component scattering model to polarimetric SAR data from forests. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2583–2592. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Maity, S.; Patnaik, C.; Parihar, J.S.; Panigrahy, S.; Reddy, K.A. Study of physical phenomena of vegetation using polarimetric scattering indices and entropy. IEEE J. Sel. Top. Earth Obs. Remote Sens. 2011, 4, 432–438. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Singh, G.; Yamaguchi, Y.; Park, S.-E. General four-component scattering power decomposition with unitary transformation of coherency matrix. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3014–3022. [Google Scholar] [CrossRef]
- Arii, M.; van Zyl, J.J.; Kim, Y. A general characterisation for polarimetric scattering from vegetation canopies. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3349–3357. [Google Scholar] [CrossRef]
- Lee, J.-S.; Pottier, E. Polarimetric Radar Imaging from Basics to Applications; CRC Press: Rochester, New York, USA, 2009. [Google Scholar]
- Semesi, A.K. Developing management plans for the mangrove forest reserves of mainland Tanzania. Hydrobiologia 1992, 1–3, 1–10. [Google Scholar]
- Ochieng, C. Research Master Plan for the Rufiji Floodplain and Delta 2003–2013; Environmental Management and Biodiversity Conservation of Forests Woodlands and Wetlands of the Rufiji Delta and Floodplain; Rufiji Environmental Management Project: Dar es Salaam, Tanzania, 2002. [Google Scholar]
- Beentje, H.; Bandeira, S. Field Guide to the Mangrove Trees of Africa and Madagascar; Kew Publishing: London, UK, 2007. [Google Scholar]
- Xtide: Harmonic Tide Clock and Tide Predictor. Available online: http://www.flaterco.com/xtide/xtide.html#contents (accessed on 10 August 2015).
- Center for Sustainability and the Global Environment. Available online: http://nelson.wisc.edu/sage/data-and-models/riverdata/station_table.php?qual=256&filenum=2130 (accessed on 10 August 2015).
- Lavalle, M.; Wright, T. Absolute Radiometric and Polarimatric Calibration of ALOS PALSAR Products Generated Within ADEN; European Space Agency: Frascati, Italy, 2009. [Google Scholar]
- Ainsworth, T.L.; Lee, J.S. A new method for a posteriori polarimetric SAR calibration. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Sydney, Australia, 9–13 July 2001; pp. 420–422.
- Lee, J.-S.; Grunes, M.R.; de Grandi, G. Polarimetric SAR speckle filtering and its implication for classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2363–2373. [Google Scholar]
- Small, D.; Holecz, F.; Meier, E.; Nuesch, D. Absolute radiometric correction in rugged terrain: A pleas for integrated radar brightness. In Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Seattle, WA, USA, 6–10 July 1998; pp. 330–332.
- Cloude, S.R. Uniquenes of target decomposition theorems in radar polarimetry. In Direct and Inverse Methods in Radar Polarimetry; Boerner, W.-M., Cram, L.A., Holm, W.A., Stein, D.E., Wiesbeck, W., Keydel, W., Giuli, D., Gjessing, D.T., Molinet, F.A., Brand, H., Eds.; Springer: Berlin, Germany, 1992; pp. 267–296. [Google Scholar]
- Cloude, S.R. Polarisation Applications in Remote Sensing; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Dickinson, C.; Siqueira, P.; Clewley, D.; Lucas, R. Classification of forest composition using polarimetric decomposition in multiple landscapes. Remote Sens. Environ. 2013, 131, 206–214. [Google Scholar]
- Praks, J.; Colin Koeniguer, E.; Hallikainen, M.T. Alternatives to target entropy and alpha angle in SAR polarimetry. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2262–2274. [Google Scholar] [CrossRef]
- Van Zyl, J.J.; Kim, Y.; Arii, M. Requirements for model based decompositions. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Piscataway, NJ, USA, 7–11 July 2008; pp. V417–V420.
- Antropov, O.; Rauste, Y.; Hame, T. Volume scattering modelling in PolSAR decompositions: Study of ALOS PALSAR data over boreal forest. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3838–3848. [Google Scholar] [CrossRef]
- Liesenberg, V.; Gloaguen, R. Evaluating SAR polarization modes at L/band for forest classification purposes in Eastern Amazon, Brazil. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 122–135. [Google Scholar] [CrossRef]
- Kobayashi, S.; Omura, Y.; Sanga-Ngoie, K.; Widyorini, R.; Kawai, S.; Supriadi, B.; Yamaguchi, Y. Characteristics of decomposition powers of L-band multi-polarimetric SAR in assessing tree growth of industrial plantation forests in the tropics. Remote Sens. 2012, 4, 3058–3077. [Google Scholar] [CrossRef] [Green Version]
- Praks, J.; Antropov, O.; Hallikainen, M. LIDAR-Aided SAR interferometry studies in boreal forest: Scattering phase center and extinction coefficient at X- and L-band. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3831–3843. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brown, I.; Mwansasu, S.; Westerberg, L.-O. L-Band Polarimetric Target Decomposition of Mangroves of the Rufiji Delta, Tanzania. Remote Sens. 2016, 8, 140. https://doi.org/10.3390/rs8020140
Brown I, Mwansasu S, Westerberg L-O. L-Band Polarimetric Target Decomposition of Mangroves of the Rufiji Delta, Tanzania. Remote Sensing. 2016; 8(2):140. https://doi.org/10.3390/rs8020140
Chicago/Turabian StyleBrown, Ian, Simon Mwansasu, and Lars-Ove Westerberg. 2016. "L-Band Polarimetric Target Decomposition of Mangroves of the Rufiji Delta, Tanzania" Remote Sensing 8, no. 2: 140. https://doi.org/10.3390/rs8020140
APA StyleBrown, I., Mwansasu, S., & Westerberg, L. -O. (2016). L-Band Polarimetric Target Decomposition of Mangroves of the Rufiji Delta, Tanzania. Remote Sensing, 8(2), 140. https://doi.org/10.3390/rs8020140