Radiometric Resolution Analysis and a Simulation Model
Abstract
:1. Introduction
2. Background
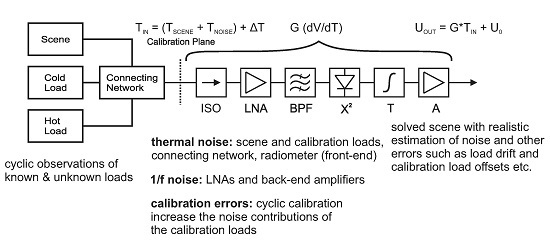
2.1. Total Power Radiometer
- , the thermal noise floor
- , gain instability
- , errors from the calibration

2.2. Noise Contribution of the FE
2.3. Noise Contribution of the BE
2.4. Noise Contribution of the Calibration Procedure
3. Instrumentation
4. Simulation Model
4.1. Simulation Model Steps
- Generate one long block of a radiometer video signal including the FE and the BE noise contributions at the calibration plane with a specific integration time τ.
- Generate a video signal for each load that the radiometer views cyclically from the above generated long video signal with a brightness temperature offset that presents a specific load. The result is a set of cycles where each cycle contain one averaged brightness temperature estimate for each measured load.
- Solve the unknowns from above determined cycle using the information derived from the known calibration load video signals. One scene brightness temperature estimate is obtained from each cycle. The result is a time stream of a solved scene brightness temperatures with a specified τ.
4.2. Radiometer Video Signal
4.3. Cyclic Observations
5. Results
5.1. Simulation Model Parameter Extraction
| Parameter | Value | Type |
|---|---|---|
| T | 342 K | known by design |
| T | 110 K | known by design |
| T | 300 K | unknown and solved |
| G | 1.44 mV/K | unknown and solved |
| U | 0 | unknown and solved |
| T | 670 K | known by measurement |
| B | 4.2 GHz | known by measurement |
| C | 0.73e-5 | known by measurement |
| N | 9 | known by design |
| α | 1.0916 | known by measurement |
| A | 961 | known by design |
| 8 nV/rtHz | known by measurement | |
| τ | 200 s | known by design |
5.1.1. Calibration Load Parameters
5.1.2. FE Parameters
5.1.3. BE Parameters
5.1.4. Integration Time

5.2. Radiometric Resolution

6. Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Racette, P.; Lang, R.H. Radiometer design analysis based upon measurement uncertainty. Radio Sci. 2005, 40. [Google Scholar] [CrossRef]
- Hersman, M.S.; Poe, G.A. Sensitivity of the total power radiometer with periodic calibration. IEEE Trans. Microw. Theory Tech. 1981, 29, 32–40. [Google Scholar] [CrossRef]
- Poutanen, T. Map-Making and Power Spectrum Estimation for Cosmic Microwave Background Temperature Anisotropies. Ph.D Thesis, University of Helsinki, Helsinki, Finland, 2005. [Google Scholar]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive; Artech House: Norwood, MA, USA, 1981; Volume 1. [Google Scholar]
- Seiffert, M.; Mennella, A.; Burigana, C.; Mandolesi, N.; Bersanelli, M.; Meinhold, P.; Lubin, P. 1/f noise and other systematic effects in the Planck-LFI radiometers. Astrophysics 2002. [arXiv:astro-ph/0206093]. [Google Scholar] [CrossRef]
- Kaisti, M.; Altti, M.; Poutanen, T. Uncertainty of radiometer calibration loads and its impact on radiometric measurements. IEEE Trans. Microw. Theory Tech. 2014, 62, 2435–2446. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaisti, M.; Altti, M.; Poutanen, T. Radiometric Resolution Analysis and a Simulation Model. Remote Sens. 2016, 8, 85. https://doi.org/10.3390/rs8020085
Kaisti M, Altti M, Poutanen T. Radiometric Resolution Analysis and a Simulation Model. Remote Sensing. 2016; 8(2):85. https://doi.org/10.3390/rs8020085
Chicago/Turabian StyleKaisti, Matti, Miikka Altti, and Torsti Poutanen. 2016. "Radiometric Resolution Analysis and a Simulation Model" Remote Sensing 8, no. 2: 85. https://doi.org/10.3390/rs8020085
APA StyleKaisti, M., Altti, M., & Poutanen, T. (2016). Radiometric Resolution Analysis and a Simulation Model. Remote Sensing, 8(2), 85. https://doi.org/10.3390/rs8020085