Improved VIIRS and MODIS SST Imagery

Abstract

Moderate Resolution Imaging Spectroradiometers (MODIS) and Visible Infrared Imaging Radiometer Suite (VIIRS) radiometers, flown onboard Terra/Aqua and Suomi National Polar-orbiting Partnership (S-NPP)/Joint Polar Satellite System (JPSS) satellites, are capable of providing superior sea surface temperature (SST) imagery. However, the swath data of these multi-detector sensors are subject to several artifacts including bow-tie distortions and striping, and require special pre-processing steps. VIIRS additionally does two irreversible data reduction steps onboard: pixel aggregation (to reduce resolution changes across the swath) and pixel deletion, which complicate both bow-tie correction and destriping. While destriping was addressed elsewhere, this paper describes an algorithm, adopted in the National Oceanic and Atmospheric Administration (NOAA) Advanced Clear-Sky Processor for Oceans (ACSPO) SST system, to minimize the bow-tie artifacts in the SST imagery and facilitate application of the pattern recognition algorithms for improved separation of ocean from cloud and mapping fine SST structure, especially in the dynamic, coastal and high-latitude regions of the ocean. The algorithm is based on a computationally fast re-sampling procedure that ensures a continuity of corresponding latitude and longitude arrays. Potentially, Level 1.5 products may be generated to benefit a wide range of MODIS and VIIRS users in land, ocean, cryosphere, and atmosphere remote sensing.

1. Introduction

More than a dozen Advanced Very High Resolution Radiometers (AVHRRs) onboard National Oceanic and Atmospheric Administration (NOAA) satellites have been in operational use since 1978. The AVHRR onboard NOAA-19 (launched in February 2009) continues functioning well as of this writing, in addition to two AVHRRs acquired by the European Organization for the Exploitation of Meteorological Satellites (EUMETSAT) for use onboard their Metop satellites. Both Metop-A (launched in October 2006) and Metop-B (launched in September 2012) work well as of today and the remaining Metop-C is scheduled for launch in 2018. With life expectancy of six years, the Metop AVHRRs will likely be in orbit through at least the mid-2020s.

The Visible Infrared Imaging Radiometer Suite (VIIRS) is a new generation US imager, developed to succeed the AVHRR in NOAA operations. The first VIIRS sensor was launched on 28 October 2011 onboard the Suomi National Polar-orbiting Partnership (S-NPP). Four more instruments are lined up to fly onboard the Joint Polar Satellite System (JPSS) satellites, J-1 to J-4 from 2017–2026. NOAA and EUMETSAT entered into a Joint Polar System agreement, by which the S-NPP/JPSS VIIRS instruments cover the afternoon (1:30 P.M./A.M.) orbit, whereas the Metop AVHRRs cover the mid-morning (9:30 A.M./P.M.) orbit.

The NOAA VIIRS sensor builds upon the NASA Moderate Resolution Imaging Spectroradiometers (MODIS) flown onboard the two Earth Observation System (EOS) Terra (10:30 A.M./P.M. orbit) and Aqua (1:30 P.M./A.M. orbit) satellites since December 1999 and May 2002, respectively. Both VIIRS and MODIS carry a comprehensive set of spectral bands, and take measurements in a wide swath to provide (near) global daily coverage, with high spatial resolution and low radiometric noise. Although the design and performance of both sensors can support accurate monitoring of atmosphere, ocean, land and cryosphere from space, VIIRS improves upon all performance metrics [1,2].

Nevertheless, both VIIRS and MODIS are affected by two major imagery artifacts: striping and bow-tie distortions. Both have multi-detector push-broom design and double side rotating mirror, introduced to improve spatial resolution and reduce radiometric noise. The VIIRS imagery is further affected by two irreversible processing steps applied onboard–pixel deletion and aggregation, which are applied to reduce the data volume prior to its down-linking to the ground. These two artifacts should be corrected before VIIRS imagery can be used for visual analysis or downstream processing.

In particular, the NOAA sea surface temperature (SST) retrieval system, Advanced Clear-Sky Processor for Oceans (ACSPO), uses some uniformity filters (within an n × n pixel spatial window) for clear-sky identification [3], and a more comprehensive pattern recognition algorithm was recently proposed [4]. Continuous, non-distorted imagery in a swath projection is a prerequisite to these algorithms. As a first step, the destriping algorithm proposed in [5] was implemented in ACSPO [6]. This paper describes simple and computationally fast methods for approximating the values deleted onboard, and for resampling VIIRS imagery in order to correct for bow-tie distortions and deletions in ACSPO Level 2 product, while preserving the originally-observed data and associated geo-locations nearly intact. In fact, the original geo values will be slightly adjusted (only the longitudes in the overlapping portions of the scans, and only at the sub-pixel level) so that the corresponding SST imagery is physically continuous (note that typically, the imagery continuity is only met after remapping, in the Level 3 and higher processing level products). This is a very important step in the direction of advanced image processing at the swath level, to facilitate improvements of the cloud mask, or perform any other processing requiring spatial continuity (e.g., computation of the gradient field). The proposed resampling should also improve other applications that use spatial information at the L2 processing, such as ocean color, cloud properties etc.

The paper is organized as follows: Section 2 describes VIIRS scan geometry. The proposed approach for VIIRS is documented in Section 3, and its application to MODIS is discussed in Section 4. Section 5 discusses results of application of the proposed algorithm with ACSPO. The alternative VIIRS imagery option, the Ground Track Mercator (GTM) projection, is considered in Section 6. Section 7 shows the potential of the proposed re-sampling approach for some additional L2 products and Section 8 summarizes and concludes the paper.

2. VIIRS Scan Geometry and Imagery

With the unprecedented advance of the remote sensing technologies, the number of data users is growing, while the satellite instruments are becoming more sophisticated. Most users and even satellite data producers may be unfamiliar with the lower-level data processing, which requires knowledge of the instrument design and specifics of onboard processing. Thus, there is a growing need for intermediate user-friendly data products such as Level 1.5 [7], in which some of the instrument-specific data issues have been mitigated.

As input, the ACSPO processing uses VIIRS L1b data (also called sensor data records, SDR [8]) in the original swath projection. Aside from striping, there are three separate issues found in VIIRS SDRs: (1) onboard aggregation; (2) bow-tie distortions; and (3) onboard deletions in the bow-tie regions. These issues are related but distinct and should not be confused. The bow-tie distortions for instance are also found on MODIS, but the onboard aggregation and deletion are unique to the VIIRS. The geometry of these procedures has to be understood and its effects on imagery mitigated, before L2 processing relying on spatial context and patterns in the imagery is possible. In what follows, we briefly describe VIIRS scan geometry and then discuss each of the above issues and their impact on ACSPO L2 product in more details.

2.1. Scan Geometry

The VIIRS Rotating Telescope Assembly (RTA) sweeps in a cross-track direction a 112.56° Earth view sector corresponding to the view zenith angle (VZA) range of ±~70° on the ground and a swath of ~3040 km in the cross-scan direction. In the along-scan direction, the 16 detectors cover a strip of approximately 11.9 km at nadir and 25.9 km wide at the end of each scan. This increase is attributed to the scan geometry and Earth’s shape, resulting in a panoramic “bow-tie” segment. A schematic of the VIIRS half-scan projection on the Earth surface from nadir to swath edge is shown in Figure 1 and the scanning footprints for three consecutive VIIRS scans are shown in Figure 2 (cf. Figure 2.2-12, p. 20 in [9] for comparison).

Figure 1. Top-left: Example of bow-tie deletions when the Visible Infrared Imaging Radiometer Suite (VIIRS) sea surface temperature (SST) image is displayed in the original swath projection. Deleted pixels are rendered in black and the land is shown in brown. Top-right: Location of the 10 min Advanced Clear-Sky Processor for Oceans (ACSPO) granule (18 October 2015 UTC) is shown by blue rectangle and its portion, displayed in the top-left, is shown in magenta. Bottom: Schematic representation of the left half of a single scan, showing bow-tie distortions, on-board deletions and aggregation for a single-gain M-band.

Figure 1. Top-left: Example of bow-tie deletions when the Visible Infrared Imaging Radiometer Suite (VIIRS) sea surface temperature (SST) image is displayed in the original swath projection. Deleted pixels are rendered in black and the land is shown in brown. Top-right: Location of the 10 min Advanced Clear-Sky Processor for Oceans (ACSPO) granule (18 October 2015 UTC) is shown by blue rectangle and its portion, displayed in the top-left, is shown in magenta. Bottom: Schematic representation of the left half of a single scan, showing bow-tie distortions, on-board deletions and aggregation for a single-gain M-band.

The neighboring whiskbrooms do not overlap at nadir but start overlapping at scan angles greater than approximately 19°. The overlap increases with scan angle and reaches ~12 km at the swath edge. However, in a swath projection, the overlapping pixels from the neighboring scans are appearing in the order they were acquired onboard, rather than according to their position on the Earth’s surface (cf. Figure 2). As a result, the L1 imagery appears distorted. Examples of these distortions (referred to herein as the “bow-tie distortions”) will be shown and analyzed in the following sections. Note that L1 imagery from both MODIS and VIIRS is subject to bow-tie distortions, although to a different degree.

Figure 2. Schematic representation of VIIRS sampling for three consecutive whiskbroom (rendered in blue, red and green respectively), for several selected VZAs from 0° (nadir) to 70° (approximately representing the left edge of the scan) in 10° increments. The two axis of each ellipse represent the horizontal and vertical sampling intervals, respectively. The vertical dashed lines show positions where the aggregation factor changes.

Figure 2. Schematic representation of VIIRS sampling for three consecutive whiskbroom (rendered in blue, red and green respectively), for several selected VZAs from 0° (nadir) to 70° (approximately representing the left edge of the scan) in 10° increments. The two axis of each ellipse represent the horizontal and vertical sampling intervals, respectively. The vertical dashed lines show positions where the aggregation factor changes.

2.2. Aggregation

The constant angular resolution of the sensor field-of-view results in an increasing pixel “footprint” projected onto the Earth for the view directions away from the nadir. For instance, the AVHRR Full Resolution Area Coverage (FRAC) and MODIS pixels grow from ~1 km at nadir to ~5–7 km, in a cross-track direction. The VIIRS instrument is subject to the same resolution degradation problem. The decision was made to employ an onboard aggregation algorithm, to reduce the variation of the pixel size across swath. At nadir, three ~0.24 km footprints are aggregated to form a single VIIRS “pixel” with a size of ~0.74 km. The aggregation changes from 3 × 1 to 2 × 1 at the scan angle ~31.589° and to 1 × 1 at 44.680° as shown in Figure 3 (cf. Figure 4 on p. 9 in [8] for comparison). The discontinuities in the pixel size due to the change in the aggregation scheme can cause artifacts during re-projection or resampling and should be treated properly.

Figure 3. The sampling interval as a function of VZA, in along-track and along-scan directions.

Figure 3. The sampling interval as a function of VZA, in along-track and along-scan directions.

2.3. Bow-Tie Distortion and Their Effect on ACSPO L2 Product

The bow-tie effect can be effectively removed by re-projecting the swath image onto a map. Therefore, users of Level 3 and higher level products never have to worry about the bow-ties. At NOAA, a limited number of VIIRS bands are processed into the imagery product, by mapping them to a Ground-Track Mercator (GTM) projection [10]. (Note that NOAA position its imagery product as an L2, although the mapping itself is an essential element of L3 processing.) The quasi-equidistant GTM grid is laid out in such a way that the columns are aligned along the ground track and the rows are positioned perpendicular to the columns. The NOAA imagery product is not subject to bow-tie artifacts and is primarily used for visual inspection of the VIIRS data. The utility of the GTM approach for SST applications is discussed later in Section 6.

As of this writing, a majority of VIIRS L2 products at NOAA are produced from L1 data on a pixel-by-pixel basis, and reported in the same swath projection. Such “in-pixel” L2 algorithms are not sensitive to the bow-tie distortions. However, some L2 algorithms do use spatial information. For instance, the ACSPO clear-sky mask employs spatial filters in which local statistics such as mean, range and standard deviation are computed over a sliding spatial window surrounding the pixel [3]. The bow-tie effects are currently ignored in ACSPO, because the re-projection is computationally expensive and there were no fast off-the-shelf algorithms easily available that preserve both the array dimensions and the corresponding geo-information. Recently, another algorithm, which uses data from the ambient pixels, was tested to smooth out the atmospheric correction term in the regression SST equations [11]. Most importantly, improvements to clear-sky mask are being explored based on patterns in the SST imagery [4]. Proper implementation of all these techniques assumes spatial continuity, which is not satisfied in the original imagery, especially at the swath edges. De-bowtizing of the L1 and/or L2 imagery is needed to improve the clear-sky mask and SST retrievals. The proposed algorithm is discussed in Section 3.

2.4. Onboard Deletions

Figure 2 shows that consecutive whiskbrooms overlap, progressively more so away from nadir, resulting in “duplicate” data. On MODIS, all data are kept and transmitted to the ground. On VIIRS, however, the decision was made to delete onboard the radiances measured in the overlapping portions of the scan, in order to reduce the data volume to be transmitted to the ground. The data in orange and magenta in Figure 1 show pixels deleted onboard the S-NPP. Simple estimates suggest that this onboard data deletion reduces the data volume by ~12.9%. When the VIIRS Raw Data Record (RDR; L0) and corresponding sensor data record (SDR; L1b) are created on the ground, the radiances in the deleted pixels are populated with fill values (whereas the corresponding geographical coordinates and angles are calculated and written to the RDR and SDR data files). These missing data on VIIRS complicate de-bowtizing and should be filled in (i.e., MODIS-like VIIRS product should be first created).

A standard way to approximate a missing value is interpolation. The simplest interpolation scheme is a nearest neighbor (NN) approach with variations on what is considered to be a “neighbor”. The best way to use a NN approach is to rely on the geographical neighbor (rather than on the closest row/column in a swath projection). Using geo-neighboring properly is intuitively straightforward, but may be computationally inefficient if the whole image has to be re-mapped first. To speed up the processing, one can remap only the values in the spatial proximity of the deleted pixels, but that again may not be fast since it requires finding the nearest neighbors for every missing value before proceeding with the estimations. Resampling of the whole image can be computationally very cheap, as will be shown later in this paper. Therefore, we first resample the L2 imagery and then perform approximation using one of the 2D spatial interpolation schemes as described in Section 3.3.

3. Re-Sampling: Requirements and Approach

To summarize the science-driven motivations, instrument-imposed specifics and real-time processing needs, our objective is a resampling that satisfies the following major requirements A_I–A_III:

A_I:

Ensures spatial continuity of the imagery;

A_II:

Provides minimal deviation from the original swath geo sampling grid;

A_III:

Is computationally fast and appropriate for real time L2 processing.

Intuitively, what is minimally required is just an unfolding procedure that reorganizes the footprints according to their geolocation (rather than in the order they were acquired by the instrument and reported in the RDR/SDR swath data files). Note that the problem of bow tie distortions in MODIS has long been recognized (e.g., [12,13,14,15,16]). The proposed solution has been remapping, whereas our objective here is to preserve the original swath projection for L2 ACSPO SST product, deferring the mapping to L3 and higher processing levels.

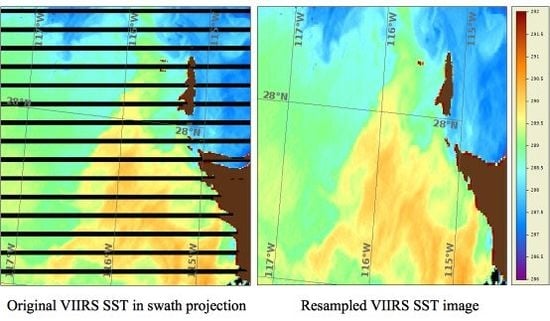
The impact of the proposed resampling approach on SST imagery can be quickly previewed from Figure 4. A small crop from a typical SST image near the end of the swath and the corresponding image of the latitude (as it appears in the SDR geolocation file) are shown in Figure 4a,b. The same latitude values, but re-ordered according to our unfolding scheme (described in Section 3.1) are shown in Figure 4c and the corresponding re-sampled SSTs in Figure 4d. The bow-ties, obviously present in the original L2 SST product (Figure 4a), are “unfolded” along with the corresponding geolocation. Re-ordering according to predefined order is computationally cheap, meets the requirements A_II and A_III and almost meets the requirement A_I (see Section 3.2 for details). The last component of the resampling procedure is the adjustment of the longitude values in the bow-tie regions (described in the Section 3.3), which satisfies the A_I and fulfills all three requirements, A_I–A_III.

Figure 4. (a) Original VIIRS SST with bow-tie distortions and deletions (note the jumps and repeats along the SST thermal fronts, and that onboard deleted pixels are shown in white); (b) original latitudes; (c) unfolded latitudes; (d) corresponding resampled SSTs.

Figure 4. (a) Original VIIRS SST with bow-tie distortions and deletions (note the jumps and repeats along the SST thermal fronts, and that onboard deleted pixels are shown in white); (b) original latitudes; (c) unfolded latitudes; (d) corresponding resampled SSTs.

3.1. Unfolding

Unfolding is basically the re-ordering according to some pattern related to the geometry of the instrument’s swath projection and the footprint locations of the scan on the Earth surface. This pattern is specific to the particular instrument and can be estimated using sorting procedures on a per-column basis for individual scan and then statistically determined based on the large set of scan-based re-ordering patterns. There are two types of VIIRS geolocation files–ellipsoid based (GMODO) and terrain corrected (GMTCO). Over ocean, the two are very close although there may be some differences due to geoid variations and in the coastal areas. In the ACSPO, the terrain-corrected GMTCO is used. However, the unfolding of the bow-tie distortions is performed in conjunction with the near elliptical Earth’s shape, which requires using the ellipsoid geolocation file, GMODO. Figure 5a,b demonstrates the effect of unfolding for three consecutive scans. The detectors are shown with 16 distinct colors, ranging from yellow (for detector 1) to blue (for detector 16). The center of the swath (the nadir) has no overlap, so the original order remains the same. In Figure 5 this corresponds to a monotonic color change within individual scans from yellow to blue.

The unfolding pattern corresponding to Figure 5a,b is illustrated in Figure 5c, for one scan S_k. Only the left half-scan is shown in Figure 5c; to extend the unfolding procedure to the right side, the table should be reflected symmetrically with respect to the nadir. The rows in the Figure 5c correspond to VIIRS detectors and the columns define the column ranges with identical re-ordering pattern.

Figure 5. Three consecutive VIIRS whiskbrooms for the left half of the scan (from the edge of the swath to the nadir): (a) in swath projection (along with sorting patterns); (b) in the mapped projection. The detectors are shown with distinct colors ranging from yellow (detector 1) to blue (detector 16); and (c) reordering scheme corresponding to the left half of the VIIRS swath. The top and bottom halves of the reordering table are displaced intentionally, to emphasize that the corresponding sorting patterns may be different (see text for details).

Figure 5. Three consecutive VIIRS whiskbrooms for the left half of the scan (from the edge of the swath to the nadir): (a) in swath projection (along with sorting patterns); (b) in the mapped projection. The detectors are shown with distinct colors ranging from yellow (detector 1) to blue (detector 16); and (c) reordering scheme corresponding to the left half of the VIIRS swath. The top and bottom halves of the reordering table are displaced intentionally, to emphasize that the corresponding sorting patterns may be different (see text for details).

Numbers in each cell represent the amount of shift for each of 16 rows in the scan S_k during the reordering. Positive values correspond to an increase of the row index and negatives correspond to the decrease of the row index. Zeros represent no change (no re-ordering). Some of the cells are color coded to facilitate the visual perception of the proposed re-ordering.

The dark blue cells, appearing together as a “ribbon” running across Figure 5c, correspond to a propagation of the last detector of the scan S_k-1, cutting through the scan S_k. The corresponding (negative) shifts, increasing in magnitude toward the end of the swath as the bow-tie overlaps increases, indicate the position of the last detector of the scan S_k-1. The lighter blue ribbon (2 cells up from the blue ribbon) corresponds to the 15nd detector of the scan S_k-1. These two ribbons are separated by a “pink ribbon” with a + 1 shift corresponding to the pixels in the same central scan, S_k (which in many cases, take the spaces on the blue ribbon). Another ribbon two more lines above, shown in cyan, stands for the 14th detector in the S_k-1. Corresponding propagation of the 1st–3rd detectors from the next scan, S_k+1, are shown in yellow-to-orange colors. In this particular case, the pattern for the propagation from S_k+1 into S_k are symmetric to that of S_k-1 into S_k, but generally speaking, this may not be always the case for the VIIRS.

3.2. Adjustments to the Generic Break Points

There are a total of 21 reordering zones determined by 20 break points, N_i, corresponding to column indexes where the reordering pattern changes. The central zone centered on the nadir (where no reordering is needed; columns 1600 and 1601) is sandwiched between N₁₀ and N_11. The break points are the positions where the grid lines of S_k intersect with the grid lines of S_k-1 and S_k+1. The upper (detectors 1 through 8) and the lower (detectors 9 through 16) parts of the table can have different break points, as the middle scan S_k can have different overlaps with the neighboring scans, S_k-1 and S_k+1, caused by a slight variation in the sub-satellite track. Our analyses of VIIRS data suggest that such scan-to-scan variations of the sub-satellite track are small but sufficient to affect the reordering positions derived as one static set. The reordering pattern is thus general, but the break points N_i’s need per-scan adjustments.

The adjustment of the initial position of an individual break point, N_k, follows the general numerical approach for finding the zero of a function, given a good initial approximation. The goal function is the distance between the elliptical latitude/longitude pair of the last detector of S_k-1 at the current break point and the geo-location of the first eight detectors of S_k (for the upper part of the scan), and the first detector of S_k and the last eight detectors of S_k+1 (for the lower part of the scan). Our implementation is using haversine formula for orthodromic distance. The schematic of the iterative procedure for break point adjustment is shown in Figure 6, where the crossing of the grid line of the 16th detector of S_k (green line) and the grid line of the 4th detector of S_k+1 (blue line) corresponds to the actual 4th break points that needs to be computed based on the initial approximation marked by the dashed dotted line in Figure 6b.

Figure 6. (a) Intersection of grid lines of S_k (green) and S_k+1 (blue). Break points are shown with red asterisks; (b) Iterative adjustment procedure: black dash-dotted line shows the column with the initial break point approximation; gray dashed lines correspond to intermediate steps of the iterative adjustment procedure with arrows indicating the direction in which adjustments occur, pointing from the current position to the next approximation. The red dashed line is the final position of the break point, which is the approximation before last in the iterative sequence, which continues until the difference between the latitude values changes the sign.

Figure 6. (a) Intersection of grid lines of S_k (green) and S_k+1 (blue). Break points are shown with red asterisks; (b) Iterative adjustment procedure: black dash-dotted line shows the column with the initial break point approximation; gray dashed lines correspond to intermediate steps of the iterative adjustment procedure with arrows indicating the direction in which adjustments occur, pointing from the current position to the next approximation. The red dashed line is the final position of the break point, which is the approximation before last in the iterative sequence, which continues until the difference between the latitude values changes the sign.

3.3. Adjusting Longitude Values

The unfolding procedure described in Section 3.1 and Section 3.2, would almost meet requirements A_I–A_III, if it would not be for the relative displacement of the consecutive scans, caused by Earth rotation. As the VIIRS instrument completes its S_k’th scan and gets ready for S_k+1’th one, the Earth has rotated by a certain amount, depending on the latitude and on the instrument scan rate. This causes the grid displacements between consecutive scans by the amount of this rotation (cf. Figure 7a for an example of displacement amounts between three consecutive scans at the end of the swath).

What really matters for the continuity assumption A_I, is the relative grid displacement with respect to the grid width. This ratio varies from the nadir to the end of the swath as shown in Figure 3. The largest relative displacement is at the nadir for the scan that sweeps through the equator. For the VIIRS instrument, this displacement can exceed the pixel width (i.e., ratio > 1), since the nominal VIIRS scan rate of 1.7864 s/scan and the speed of the Earth rotation at the equator is 2*pi*6380/(24*3600) km/s, resulting in the shift of ~0.828 km between the scans, which is larger than the 0.75 km pixel width at the nadir. However, there is no bow tie effect at the nadir, and reordering is done for columns 1:1307 and 1893:3200, where the pixels grow larger than 0.75 km. The relative displacement as a function of latitude and the pixel location in the swath (for the left half the swath) is shown in Figure 7b. The orange-to-red values of the 2D relative displacement surface indicate the cases, where the relative scan displacement exceeds one pixel. This happens in the low latitudes (tropics) around the nadir position and at the beginning of each aggregation zone. The shifts at the end of the swath are at a sub-pixel level (in agreement with the example shown in Figure 7a).

Figure 7. (a) The geo-locations of three consecutive VIIRS scans near the end of the swath are shown in green, red and blue. Portions of the scans corresponding to onboard deletions are marked by dashed line; (b) Relative scan displacement as a function of latitude and scan position.

Figure 7. (a) The geo-locations of three consecutive VIIRS scans near the end of the swath are shown in green, red and blue. Portions of the scans corresponding to onboard deletions are marked by dashed line; (b) Relative scan displacement as a function of latitude and scan position.

Figure 8a shows the grid overlap between scans S_k and S_k+1, around the transition from the 3:1 to the 2:1 aggregation zone. It is small but not negligible. The order of grid pixels-as they appear in a particular column of latitude and longitude arrays after unfolding-is traversed with magenta arrows. The zigzagging magenta path is caused by Earth rotation between consecutive scans, and the need to keep the swath projection non-displaced from one scan line to another. As long as the zigzagging is within the footprint boundaries (i.e., the gridlines do not cross), the continuity (requirement A_I) is satisfied. The zigzagging exceeding the grid cell can affect the quality of the reordered SST imagery. It is especially noticeable along ocean thermal fronts or other features on the surface with large gradients.

Figure 8. (a) Geo-locations around the transition from the 3:1 to the 2:1 sample aggregation scheme; magenta path connects interleaved footprints from different scans; (b) two alternate geo reordering schemes, involving column shifts, marked by yellow and orange paths.

Figure 8. (a) Geo-locations around the transition from the 3:1 to the 2:1 sample aggregation scheme; magenta path connects interleaved footprints from different scans; (b) two alternate geo reordering schemes, involving column shifts, marked by yellow and orange paths.

One possible alternative to preserve the values of the original geo-grid and to mitigate the zigzagging effect is to additionally reorder columns. An example of such possible reordering is shown in Figure 8b with two alternative orders (marked by yellow and orange paths, respectively). Both paths would require a change of the original 3200 column setting to allow for the shifts persistently present between consecutive scans. A more attractive approach was deemed to (slightly) adjust the longitudes, which also ensures the spatial continuity while preserving the swath width intact. An example of this adjustment is shown in Figure 8b, with the new grid lines marked by dotted lines and new grid points by black dots. Note that only the longitudes are (slightly) changed, while the latitudes are reordered but not modified. The grid overlaps for scans S_k-1, S_k, and S_k+1 around the transition from the 2:1 to the 1:1 sample aggregation scheme are shown in Figure 9.

Figure 9. Geo-locations around the transition from the 2:1 to the 1:1 sample aggregation scheme. Unfolding order for this region corresponds to the N₅ +1:N₆ column of Figure 5c with only six middle detectors, 6 through 11, outside the bow-tie region. The insert on the left shows detailed overlap of the S_k and S_k+1 grids. Black zigzagging line represents reordered path and black dotted line corresponds to proposed grid with adjusted longitude values.

Figure 9. Geo-locations around the transition from the 2:1 to the 1:1 sample aggregation scheme. Unfolding order for this region corresponds to the N₅ +1:N₆ column of Figure 5c with only six middle detectors, 6 through 11, outside the bow-tie region. The insert on the left shows detailed overlap of the S_k and S_k+1 grids. Black zigzagging line represents reordered path and black dotted line corresponds to proposed grid with adjusted longitude values.

The overlap due to bow-ties is significant and the unfolding order for this region corresponds to the N₅+1:N₆ region of Figure 5c. The latitude and longitude values for one column in this region zoomed into two scan’s overlap are plotted in Figure 10 (top plot). The blue line in the latitude plot corresponds to the original scan order. The black dotted line (top plot of Figure 10) shows the latitude values after reordering, which makes the plot monotonic. Reordered longitudes, shown in a black solid line in Figure 10 (bottom plot) have a zigzagging pattern, as expected due to the described relative scan displacement. Simple (and computationally fast) 1D per-column interpolation, preserving the longitudes that have not been reordered (cf. cells with “0” entries in Figure 5c), results in the monotonic longitude values shown in magenta. Adjustments to the longitudes are only done for the reordered pixels. The corresponding modified grid is shown in the insert of Figure 9, where the gridlines are marked by black dotted lines and black dots correspond to new (longitude-adjusted) geo-locations.

Figure 10. Top: Latitude values for the middle column of the grid portion shown in Figure 9. Blue line represents original latitude values and black line corresponds to latitudes reordered according to Figure 5c. Bottom: Longitude values for the same column. Black line corresponds to longitudes reordered according to Figure 5c. Zigzagging effect caused by Earth rotation is present at the bow-tie regions after reordering. Magenta line, representing adjusted longitudes, is monotonic. The adjustments are performed only at the overlapping portions of the consecutive scans.

Figure 10. Top: Latitude values for the middle column of the grid portion shown in Figure 9. Blue line represents original latitude values and black line corresponds to latitudes reordered according to Figure 5c. Bottom: Longitude values for the same column. Black line corresponds to longitudes reordered according to Figure 5c. Zigzagging effect caused by Earth rotation is present at the bow-tie regions after reordering. Magenta line, representing adjusted longitudes, is monotonic. The adjustments are performed only at the overlapping portions of the consecutive scans.

Note that some (but not all) of the pixels whose longitudes are adjusted, correspond to the deleted onboard data (orange and magenta pixels of Figure 1), making changes to their geolocation easier to justify. For the resulting de-bowtized imagery to be used for image-processing SST applications, the missing radiances in the deleted pixels should be evaluated.

3.4. Approximation of the Deleted Values

With all of the reordering work done, the estimating of the missing values is a straightforward task: in the resampled imagery, the index-based neighbors are now also geo-neighbors, which makes distance-based weighted averaging a simple and well-justifiable option. For each onboard deleted value, we use the four closest (±1 row/column) neighbors and compute the Gaussian-weighted average with standard deviation proportional to the corresponding vertical footprint size. There might be some flagged values among those neighbors due to the present deletion/reordering scenario, but a closer look at Figure 5c reveals that there are always some non-deleted entries among the selected four horizontal/vertical neighbors. There might be cases when all four neighbors are flagged for some other reason (not relevant to onboard deletion). All of the flagged values are excluded from the averaging procedure, and when all four neighbors are flagged, then the deleted pixel is marked as invalid.

An example of resampled brightness temperature BT at 12 μm with estimated values in the deleted zones is shown in Figure 11c. For comparison, the original BT at 12 μm is given in Figure 11a. The presented crop is selected from the 10 min ACSPO granule acquired on 1 December 2015 at 21:40 UTC. “Repeats” typical for bow-tie distortions, which were apparent in Figure 11a, are not present in the unfolded reordered image shown in Figure 11b. The re-ordered image in Figure 11b also reveals the variation of the break-points, discussed in the Section 3.2. A zigzagging pattern, especially noticeable along thermal fronts, is also noticeable in the re-ordered image. Corrections to the longitude values, discussed in Section 3.3, undo the zigzagging artifacts caused by the shifts, as can be seen from resampled image in Figure 11c. The image shown in Figure 11c now meets all the A_I-A_III requirements above, and ready for all planned SST imagery-based enhancements at NOAA.

Figure 11. BT at 12 μm: (a) Original; (b) Reordered; (c) Resampled with missing values filled.

Figure 11. BT at 12 μm: (a) Original; (b) Reordered; (c) Resampled with missing values filled.

4. Resampling for MODIS

MODIS instrument has fewer detectors (10 vs. 16), coarser pixel resolution (1 vs. 0.74 km at nadir; ~5 vs. 1.5 at swath edge), faster scan rate (1.478 vs. 1.786 s per scan), narrower swath (2330 vs. 3040 km). Otherwise, it is similar to VIIRS instrument: in particular, it is also subject to bow-tie distortions. A schematic of the MODIS half-scan projection on the Earth surface from nadir to swath edge is shown in Figure 12a [10]. The unfolding algorithm described in Section 3 can be directly applicable to MODIS, except its implementation is simpler, as there are no pixel aggregations or onboard deletions. Also, there is no need for the recalculation of the original longitudes, because the scan-to-scan displacement due to Earth rotation (~0.685 km in worst case scenario, at the nadir and at the equator) is smaller due to faster scan rate, and the displacement is always smaller than the pixel size. The reordering table for MODIS is given in Figure 12b. Note also that the break point adjustments are not needed for MODIS, because the displacements between consecutive scans are much more regular for both Aqua and Terra satellites than for the S-NPP. This is fortuitous because in MODIS L1b data, only terrain corrected geolocation is reported and the ellipsoid based geo locations (not rectified for terrain) are not readily available.

Figure 12. (a) Schematic representation of Moderate Resolution Imaging Spectroradiometer (MODIS) sampling for three consecutive whiskbrooms (rendered in blue, red and green respectively), for several selected VZAs from 0° (nadir) to 65° (approximately representing the left edge of the scan) in 10° increments. The two axis of each ellipse represent the horizontal and vertical sampling intervals, respectively; (b) The reordering scheme for the left half of the MODIS swath.

Figure 12. (a) Schematic representation of Moderate Resolution Imaging Spectroradiometer (MODIS) sampling for three consecutive whiskbrooms (rendered in blue, red and green respectively), for several selected VZAs from 0° (nadir) to 65° (approximately representing the left edge of the scan) in 10° increments. The two axis of each ellipse represent the horizontal and vertical sampling intervals, respectively; (b) The reordering scheme for the left half of the MODIS swath.

5. Results and Evaluation

The impact of the proposed resampling on the performance of the current ACSPO clear-sky mask (ACSM; [3]) was initially evaluated and reported here. Recall that two ACSM tests—the “SST filter” and the “spatial uniformity check”—employ information in spatial windows surrounding the pixel [3]. In the resampled data, the performance of these two tests is expected to improve, i.e., to reduce the number of the corresponding “false alarms”, and the number of clear-sky ocean pixels, CN, and the corresponding clear-sky fraction, CF (defined as a ratio of clear-sky to the total number of ocean pixels), to increase.

To verify this expectation, global ACSPO products have been generated from Aqua and Terra MODIS (each containing 288 5-min granules) and S-NPP VIIRS (144 10-min granules), for one full day of global data (18 October 2015). Two ACSPO runs were performed: with the original SDR data and with the resampled SDRs. In what follows, the results of the runs are analyzed, with emphasis on the effect of resampling. Cross-platform differences (which may result from different spatial resolution, radiometric quality, and different overpass times) are relatively small and not analyzed here.

Number of clear-sky ocean pixels, CN, and the corresponding clear-sky fraction, CF, are shown in Table 1. For all sensors, the CN derived from the original SDRs is smaller than from the resampled SDRs. For the VIIRS, the increments are much larger than for MODIS. Recall that they include 12.9% of VIIRS pixels which have been deleted onboard (see Section 2.2). In contrast, the corresponding resampled VIIRS CFs (right Table) are only slightly larger. For VIIRS, two mutually offsetting mechanisms are responsible for the change in the CF. First, the deleted pixels are filled in from the four neighbors, and there is a high probability that at least one of them is cloudy. As a result, the filled pixels are expected to have a “cloudy” bias, which should lead to a decrease in the CF. On the other hand, the improved spatial uniformity due to resampling is expected to result in the improved ACSM, and larger CF. As Table 1 suggests, the improvements in the SST imagery (and consequently, in the ACSM) outweigh the “cloudy” bias in the filled pixels, resulting in a net absolute increase of 0.2% in the CF (average between day and night). In a relative sense, this delta is equivalent to an increase in the clear-sky sample by 1%, globally. For MODIS, there are no deleted pixels and no corresponding offsetting mechanism, and therefore a larger improvement is expected. Table 1 shows that indeed, the absolute increment between Terra and Aqua, day and night, is from 0.4% to 0.6% (approximately 2%–3% increase in the clear-sample).

Table 1. Top: Number of clear-sky ocean pixels, CN (millions). Down: Corresponding clear-sky fraction, CF (percent to total number of ocean pixels observed by the corresponding sensor). Data are from one full global day on 18 October 2015.

	Day		Night
	Original	Resampled	Original	Resampled
S-NPP VIIRS	129.0	148.0	112.9	131.7
Aqua MODIS	48.1	49.0	40.9	42.2
Terra MODIS	47.3	48.3	44.4	45.8
	Day		Night
	Original	Resampled	Original	Resampled
S-NPP VIIRS	21.00	21.10	18.87	19.20
Aqua MODIS	21.46	21.87	18.91	19.47
Terra MODIS	21.74	22.17	20.57	21.21

Table 1. Top: Number of clear-sky ocean pixels, CN (millions). Down: Corresponding clear-sky fraction, CF (percent to total number of ocean pixels observed by the corresponding sensor). Data are from one full global day on 18 October 2015.

	Day		Night
	Original	Resampled	Original	Resampled
S-NPP VIIRS	129.0	148.0	112.9	131.7
Aqua MODIS	48.1	49.0	40.9	42.2
Terra MODIS	47.3	48.3	44.4	45.8
	Day		Night
	Original	Resampled	Original	Resampled
S-NPP VIIRS	21.00	21.10	18.87	19.20
Aqua MODIS	21.46	21.87	18.91	19.47
Terra MODIS	21.74	22.17	20.57	21.21

Figure 13 (left panels) additionally shows the CF (day and night combined) as a function of view zenith angle (VZA). For both sensors, the CF is largest around nadir (~22%–24%) and drops off to ~10%–15% at the swath edges. The resampled data always have a comparable or larger CF, in all bins. The relative differences between the two grey curves are shown on the right. The improvement is insignificant around nadir, and progressively increases towards swath edges, where it reaches from 6% to 8% for the VIIRS and from 9% to 12% for MODIS. The increment is a little larger at night, likely due to the use of reflectances during the daytime, which may be more subject to artifacts in visible imagery and result in higher screening rate.

Additional analyses (not shown here) suggest that the global statistics of the newly added SSTs are comparable to, or better than those derived from the original SDRs. Recall that a distinctive feature of the ACSPO SST product, compared to other partners’ SST retrievals systems, is that retrievals are made in the full sensor swath. Increase by up to 8%–12% in the valid SST data rate at the slant view geometries (which recall are least populated with the retrievals and characterized by degraded observational conditions) is instrumental to provide more complete global coverage by the ACSPO SST product. Note that this assessment was done with the current ACSPO clear-sky mask, which minimally uses spatial information. The improvement is expected to be more significant with implementing the pattern recognition techniques [4], at which time the potential of the improved SST imagery will be more fully realized.

Figure 13. Number of clear sky observations for one day (18 October 2015) of global ACSPO SST data as a function of view zenith angle (VZA) for (a) S-NPP VIIRS; (b) Aqua MODIS; (c) Terra MODIS. Original data are shown in light gray and resampled in dark gray. Day and night data are combined together. Corresponding percent increase for (d) S-NPP VIIRS; (e) Aqua MODIS and (f) Terra MODIS (separated by night and day).

Figure 13. Number of clear sky observations for one day (18 October 2015) of global ACSPO SST data as a function of view zenith angle (VZA) for (a) S-NPP VIIRS; (b) Aqua MODIS; (c) Terra MODIS. Original data are shown in light gray and resampled in dark gray. Day and night data are combined together. Corresponding percent increase for (d) S-NPP VIIRS; (e) Aqua MODIS and (f) Terra MODIS (separated by night and day).

6. Comparison with Ground Track Mercator (GTM) Projection

As mentioned earlier in the paper, NOAA generates a GTM VIIRS imagery product, which is free of bow-tie artifacts including the stripes of missing data caused by onboard deletions. The GTM algorithm also suppresses the discontinuities at the switch from one aggregation scheme to another. The measured digital counts (DC) are carried unaltered from the original row-column locations in the swath projection to the closest GTM grid position using nearest neighbor (NN) approach.

Overall, the GTM algorithm successfully removes the most obvious imagery issues and improves the VIIRS imagery. However, the NN implementation may introduce some other artifacts, which may not be as obvious from the visual perception, but nevertheless problematic for image processing that requires spatial information. A small, zoomed-in patch from the edge of the VIIRS swath is shown in Figure 14a. The original geo locations (dots) and corresponding grids (lines) are shown in blue, with the pixels deleted onboard rendered in magenta. The GTM data are shown in black (again, dots representing centers, and lines the corresponding grids). Red dashed arrows pointing to the GTM black dots indicate the DCs copied from the original swath data to the GTM locations. As can be seen from Figure 14a, some of the original DCs are duplicated (actually, one swath point may be reused up to four times). This will imply bias in computations of horizontal, vertical or both components of the (numerical) gradient. Such duplications will also bias the statistics computed within small spatial windows.

The replication patterns do change depending on the location within the scan, but the distribution of number of duplicates within the scan can be estimated by simply counting the number of identical DCs in the horizontal (identical DC values at (i,j) and (i,j + 1) location) and vertical (identical values at (i,j) and (i + 1,j) locations). Percentage of locations with the same values to the right (horizontal duplicates) and to below (vertical duplicates) are shown in Figure 14b. Toward the end of the scan, the percent is as large as 50% for both, vertical and horizontal count. As intuitively expected, the distribution of the horizontal duplicates closely follows the discontinuities inherited from the three different aggregation schemes. A more thorough analysis of GTM projection, its artifacts and impact on other products is beyond the scope of this paper. Our goal is improved clear-sky mask for SST and calculation of ocean thermal fronts (gradients). To that end, the re-sampling procedure proposed here is deemed a more fit-for-purpose imagery improvement technique compared to the GTM projection.

Figure 14. (a) Small crop from the end of the swath showing both grids: original swath (blue) and GTM (black). Pixels deleted onboard (magenta) would decrease the number of duplications in the GTM projection; (b) Distribution of GTM duplicates: (top) horizontal and (bottom) vertical. The bar graph uses 121 columns in each bin, except for the last bin.

Figure 14. (a) Small crop from the end of the swath showing both grids: original swath (blue) and GTM (black). Pixels deleted onboard (magenta) would decrease the number of duplications in the GTM projection; (b) Distribution of GTM duplicates: (top) horizontal and (bottom) vertical. The bar graph uses 121 columns in each bin, except for the last bin.

7. Potential Benefits of Resampling for other Level 2 Products

The resampling procedure described here is a general algorithm that is specific to the instrument rather than to the derived L2 product. Although it was motivated by, and originally developed for the SST applications, it can be successfully used for other L2 products and applications as well. One such example is presented below, to illustrate its potential for ice analysis.

Figure 15 shows a 400 × 400 pixel crop taken at the end of the VIIRS swath for the 20:27:42.7 and 20:29:08.1 UTC passes on 1 September 2015 over Arctic Ocean. The crop in Figure 15 includes Qikiqtaaluk Region (Nunavut, Canada) showing a part of the Northwestern Passage, Axel Heiberg, and Ellesmere Islands containing mountainous and glaciated terrain.

The White Glacier located on the Axel Heiberg Island shows the ice remaining here after the hot summer of 2015. This glacier has the longest continuous mass balance record of all high Arctic glaciers, and has been shrinking for the past two decades. There are multiple ice floats in the Sverdrup Channel, as well as a single ice float just above Eureka. The fine-scale details captured by the VIIRS instrument are preserved during the proposed resampling procedure. The difference between original M4 (0.55 μm) and M10 (1.6 μm) bands is shown in Figure 15a and its resampled counterpart in Figure 15b. The M4–M10 is the key feature widely employed for snow and ice applications. The ice patterns are much more pronounced and form more continuous patterns in the difference image.

The difference between terrain-corrected and ellipsoid longitudes in the original scan order (from GMTCO and GMODO VIIRS geo files) is shown in Figure 16a, and after resampling in Figure 16b. The elevation patterns attributed to Earth terrain are clearly seen in the de-bowtized resampled imagery, Note that resampled values of GMTCO are reported in ACSPO files, and Figure 16b suggests that that not only the SST imagery is approved but also the corresponding geolocation.

Figure 15. (a) Difference between original M4 (0.55 μm) and M10 (1.6 μm) bands; (b) difference between resampled M4 and M10.

Figure 15. (a) Difference between original M4 (0.55 μm) and M10 (1.6 μm) bands; (b) difference between resampled M4 and M10.

Figure 16. (a) Difference between terrain-corrected and ellipsoid longitudes in the original scan order (from VIIRS Moderate Bands SDR Terrain Corrected Geolocation (GMTCO) and Original (elliptical) Geolocation (GMODO) files); (b) De-bowtized difference after re-sampling.

Figure 16. (a) Difference between terrain-corrected and ellipsoid longitudes in the original scan order (from VIIRS Moderate Bands SDR Terrain Corrected Geolocation (GMTCO) and Original (elliptical) Geolocation (GMODO) files); (b) De-bowtized difference after re-sampling.

8. Conclusions

Today VIIRS, along with its predecessor MODIS, remain the best suite-for-purpose US polar SST sensors in space. Their superior performance, including the high spatial resolution and low radiometric noise, is achieved by using push-broom technology, when multiple detectors are used to simultaneously collect measurements from several scan lines. The flipside of the multi-detector sensor design is striping and bow-tie distortions in the satellite imagery. Special pre-processing to minimize these instrumental artifacts and ensure spatial continuity of satellite imagery is critically important for users interested in satellite imagery, and in processing spatial patterns using the machine learning algorithms [4]. The NOAA JPSS SST Team has implemented a destriping algorithm in the NOAA SST ACSPO version 2.40, which became operational in May 2015. Work is underway to implement the bow-tie correction algorithm documented in this paper for the VIIRS and MODIS data in ACSPO version 2.50. The objective of these two releases is to set the stage for implementing the pattern recognition improvements described in [4] in ACSPO version 2.60.

Note that NASA which was responsible for the MODIS sensor onboard EOS Terra and Aqua satellites has opted to not correct for the effects of striping and bow-tie distortions. The intention was to keep the MODIS radiances and geolocation in Level 1 and 2 products intact (as measured). However, the mission of the NOAA National Environmental Satellite Data and Information Service (NESDIS) is serving its users data which are easy to display, use and understand. This requires minimization of the specifics of individual measurements, and emphasizing sensor data which are as artifact-free as possible. To that end, the EUMETSAT (a European counterpart of NESDIS, whose objective, similarly to NESDIS, is serving artifact-free data to the Numerical Weather Prediction customers and other users of satellite data) has generated a Level 1.5 data from the Spinning Enhanced Visible and Infra-Red Imager (SEVIRI) onboard the Meteosat Second Generation (MSG) satellite [7]. In SEVIRI Level 1.5 data, differences in detector responses are equalized, nonlinearity of the sensor response is corrected for, and the satellite imagery is converted into a standard reference projection (including the co-registration between channels) [7]. Therefore, radiances and geolocation on SEVIRI Level 1.5 are (slightly) changed from those measured onboard, but these adjustments proved extremely beneficial to the users of the SEVIRI data. Those science and sensor-analysis oriented users, who are interested in the original sensor data “as measured”, can always resort to a Level 0 or 1 data.

From the Advanced Himawari Imager (AHI) onboard the Japanese new generation geostationary Himawari-8 satellite, the Japanese Meteorological Agency (JMA) produces a Level 1 product, using a processing philosophy similar to the one adopted in SEVIRI Level 1.5. The Advanced Baseline Imager (ABI) to be launched onboard the new generation GOES-R series will also report a geometrically corrected, radiometrically-equalized imagery. Discussions are also underway at NOAA to generate a VIIRS Level 1.5 product, which will be identical in the data format to the current VIIRS SDRs (L1b), but will include bow-tie corrected (filled-in and re-sampled, and potentially destriped) imagery. The JPSS SST Team strongly supports such intermediate product, as it will reduce the burden on the SST processing. We firmly believe that this processing should be done upstream, and it will benefit other JPSS L2 products, not only SST. Should NOAA decide to pursue the L1.5 route for the VIIRS, it is strongly recommended that the original L0 (RDR) and L1b (SDR) data are fully available and easily accessible to the users.

It has been suggested that the unfolded product is good for visual analysis, usable for inter-pixel tests (e.g., uniformity) and for SST evaluation, but may not be appropriate for any serious estimations of global climatic parameters or statistics, and therefore it should not be used as a data source for generating Level 2 and 3 products. In the next version of ACSPO product (v2.50), the resampled L2 imagery will be reported. We initially planned to fix the bow-tie distortions, and fill in deleted pixels, as an intermediate step and then restore the original VIIRS projection. However, many users of VIIRS data have issues with these artifacts, and therefore the decision was made to preserve the resampled imagery in the output files. Recall that for the vast majority of pixels, the geo-location will not change (only reordered to satisfy the requirement of local monotonicity). The percent of pixels, where geo-location has to be adjusted (by less than the footprint width) to preserve the alignment between different scan lines is very small. All VIIRS pixels filled in the bow-tie deletion areas, will be flagged as such, so it will be up to L3/4 producers whether or not to use those. However, all users of ACSPO data relying on SST imagery, will greatly benefit from the improved appearance of the product.

One can expect that the future satellite sensors will be as (or even more) complex as the current VIIRS and MODIS to ensure high resolution, low noise measurements in multiple spectral bands. Therefore the striping and bow-tie artifacts will likely continue to be present. Satellite data processing experts should therefore consider users’ needs in simple, intuitive, and easy to understand and use sensor data. Generating a Level 1.5, and keeping it along with the raw data records (RDR; Level 0) or SDR (Level 1b) data in the NOAA archives, may be a practical compromise. We also strongly recommend avoiding the current onboard deletion of VIIRS pixels in bow tie areas, which degrades the data and further complicates the imagery improvements.