Monitoring Riverbank Erosion in Mountain Catchments Using Terrestrial Laser Scanning

Abstract

Sediment yield is a key factor in river basins management due to the various and adverse consequences that erosion and sediment transport in rivers may have on the environment. Although various contributions can be found in the literature about sediment yield modeling and bank erosion monitoring, the link between weather conditions, river flow rate and bank erosion remains scarcely known. Thus, a basin scale assessment of sediment yield due to riverbank erosion is an objective hard to be reached. In order to enhance the current knowledge in this field, a monitoring method based on high resolution 3D model reconstruction of riverbanks, surveyed by multi-temporal terrestrial laser scanning, was applied to four banks in Val Tartano, Northern Italy. Six data acquisitions over one year were taken, with the aim to better understand the erosion processes and their triggering factors by means of more frequent observations compared to usual annual campaigns. The objective of the research is to address three key questions concerning bank erosion: “how” erosion happens, “when” during the year and “how much” sediment is eroded. The method proved to be effective and able to measure both eroded and deposited volume in the surveyed area. Finally an attempt to extrapolate basin scale volume for bank erosion is presented.

1. Introduction

The study of sediment yield as well as sediment erosion in mountain catchments has been receiving increasing attention from scientists in the last decades. Soil erosion has several on-site and off-site impacts on the environment: (1) loss of fertile soil with important consequences on agriculture [1]; (2) silting of reservoirs that reduces the storage capacity and interferes with dam operations [2,3,4]; (3) migration of pollution in which sediment transport is considered a means of transport for contaminants [5,6]; (4) increase of flood risk [7] and debris flow events [8]; and (5) geomorphic evolution of river beds [9] with possible impacts on the surrounding structures. At the basin scale, sediment production is the result of the complex interaction between different geomorphic processes: splash erosion, sheet erosion, rill erosion, gully erosion, bank erosion as well as mass movements [10]. However, not all processes are equally contributing in different basins. In fact, according to De Vente and Poesen [11], the dominant sediment source varies with the dimension and the type of basin. The problem of sediment yield and erosion rate estimation in mountain catchments requires an overview of the active erosion processes and, even more importantly, a quantification of the contribution of each process to the sediment transport into the stream.

Among the aforementioned sediment sources, riverbank erosion is considered a rather significant process in the context of fluvial dynamics as it involves a considerable fraction of the total sediment yield being supplied by riverbanks although its contribution varies between rivers [12,13,14,15]. Riverbank erosion may be caused by different phenomena, occurring with differing magnitudes and frequencies [16,17]. These have been summarized by Lyons et al. [18] as: (1) detachment of bank material induced directly by the fluvial activity; (2) mass wasting under the effect of gravity on an undercut or unstable bank; (3) sub-aerial influence as a result of hydrometeorological variations such as freeze-thaw cycles and change in soil moisture; and (4) riverbank destabilization due to groundwater seepage.

Investigating the spatial and temporal variations of riverbank erosion is a key point in understanding and monitoring the development of rivers as well as for estimating rates of sediment production [19]. Riverbanks in mountain areas are subject to high-energy flows as well as rapidly varying meteorological conditions, which makes them particularly susceptible to different instabilities and erosive activity with possible implications even in terms of flash floods involving large quantities of eroded material and resulting in enormous morphological changes [20,21]. The use of terrestrial laser scanning (TLS) [22,23] has become a well-established practice for detecting riverbank relief changes at different scales [24,25,26,27]. TLS may provide in a straightforward manner a detailed 3-D point cloud describing the topographic surface of the investigated area. By adopting a stable reference frame (e.g., [24,28]), multiple data sets can be compared to detect and map surface changes indicating erosion and/or deposition areas [19,27,29,30,31,32]. In particular, the ground-based location of the adopted laser scanning sensor can be exploited to obtain a suitable view over even steep riverbanks, as opposed to airborne laser scanning (ALS) which may encounter severe limitations to survey vertical banks. TLS exhibits various advantages over the use of other conventional methods such as erosion pins and total station surveying, which cannot provide the same spatial resolution and need longer time for data acquisition (see Section 3.1).

Few efforts were conducted on the general analysis of the riverbank erosion process in mountain areas. In most cases, long time gaps between successive surveys are present, leaving some uncertainty on the triggering factors of erosion and its link to the climate conditions.

Considering the complexity of riverbank dynamics, in a wider perspective of improving the knowledge on this topic, the authors seek to provide a quantitative analysis of the riverbank erosion through the use of laser scanning technique. Four riverbanks located in an Alpine Area in Northern Italy have been investigated using TLS. Collected data allowed the authors to consider three fundamental issues related to the riverbank erosion process:

1

the overall kinematic behavior of the riverbank (by mapping erosion and deposition areas) that may influence the storage of sediments as well as the sediment transport into the river;

2

the relationship between riverbank erosion and seasonal features (rainfall and freeze-thaw cycles); and

3

the amount of sediment yield produced.

The mountain catchment selected for this experimental study was chosen due to the presence of several active erosion processes as well as the availability of data concerning reservoir siltation. After a brief presentation of the main geological and geomorphic features of the case study (Section 2), the methodology used to measure the riverbank erosion during one year will be explained in Section 3. The results obtained from the processed data as well as the uncertainties associated to them will be discussed in Section 4 in order to address the aforementioned issues, which may be summarized as “how”, “when”, and “how much” riverbank erosion occurred. Finally, some conclusions and suggestions for the advancement of this research will be drawn in Section 5.

2. Presentation of the Study Area

The case study discussed in this paper is composed of four riverbanks located in the Tartano Valley, an Alpine catchment in the North of Italy, 100 km away from Milan (Figure 1). Due to its hydrogeological peculiarities many authors focused their attention on this catchment [33,34,35]. The elevation of the basin varies in the range between 950 m and 2250 m a.s.l., with a mean altitude of 1861 m a.s.l. The main river in this valley, called the Tartano River, is a left tributary of the Adda River and in its upstream portion is divided in two secondary streams—Val Lunga and Val Corta. Downstream, the Tartano River flows in a wide alluvial fan that spreads over an area of approximately 2 km². As indicated in Figure 1, this river is blocked by a dam (the Campo Dam).

The basin is characterized by an Alpine continental climate. Regarding the landuse, the anthropic presence in the catchment is very limited. Instead, more than 40% of the basin is covered by a coniferous forest. The availability of annual sediment yield data for the reservoir of Campo Dam (with an average value of 38,000 m³/year as reported by Brambilla et al. [36]) makes the upstream catchment a prototypal case to calibrate and validate models for erosion forecast. Several flooding events have been documented in this valley. The most catastrophic event happened in 1987, in which the strong rainfall event combined with snowmelt caused a flood, several debris flows and one mass movement. The latter eventually resulted in 20 casualties. During this rainfall event, bank protections were destroyed and the total sediment at the fan was estimated to be approximately one million cubic meters.

2.1. Geological and Geomorphic Setting

The Tartano Valley is located on the southern side of Valtellina and its bedrock belongs to the Gneiss di Morbegno formation, the metamorphic rocks of the Orobic Basement [37]. Two nearly vertical fault systems intersect the bedrock with NE-SW and NW-SE strikes.

The entire catchment is characterized by the presence of several shear zones along these faults. According to Ramsay [38] these areas are considered weak zones, prone to instability. These faults have clearly influenced the geometry of the stream network. For instance, Val Corta belongs to the NE-SW fault system, while Val Lunga belongs to the NW-SE system instead.

The rock basement is often covered by talus and debris material due to alluvial, colluvial and glacial deposits of a rather limited thickness that can locally reach up to 10 m. A great amount of sediments is located along the described faults and intense rainfall events may be able to mobilize this material. In addition to the presence of these widespread mass movements, two main landslides are located in this basin: the Pruna landslide and the Foppa dell’Orso landslide. The Pruna landslide is located downstream of the dam and therefore, sediment yield from this slope plays a crucial role in the fan dynamics. The Foppa dell’Orso landslide is a shallow mass movement located on the left bank at the end of Val Lunga, upstream of the dam. Therefore, this landslide may also be considered as a sediment source for reservoir siltation.

2.2. Testbed: Riverbanks in Tartano Valley

The active geomorphic processes in the entire basin that contribute to the sediment transport into the river are linked to its geological and structural features. Therefore, the areas prone to erosion may be recognized in fault rocks, debris deposits and landslide areas. The significance of riverbank erosion with respect to the total sediment yield in mountain catchments is not explicitly taken into account by models predicting erosion rates. Instead, such models are designed to estimate the sediment yield as a result of several or all the ongoing erosion processes in a basin, without any consideration on the individual contribution of each one [11]. In Brambilla et al. [36], the Gavrilovic method, a model capable to take into account sheet, rill, gully, and bank erosion was applied to the same catchment. However, the features of riverbank erosion as well as the role of this single process in the total sediment yield is still unknown.

Starting from this point, the authors focus their attention on four banks located in this valley (Figure 1). The resistance of natural riverbanks to erosion is closely related to the geomorphic characteristics of the bank itself (Figure 2). Thus, four banks representative of different conditions of the river are chosen. The features of the testbeds are reported in

Table 1. Geometrical, geological and morphological aspects of the banks used in the experimental study.

Bank	Type of Material	Dimensions (m)		Slope	River–Bank Interaction	River Morphology
		Height	Length
1	Glacial and fluvial deposit	2.9	93	71°	Only with Exceptional discharge	Straight, after a bottleneck
2	Glacial and fluvial deposit with the presence of some boulders	2.8	20	49°	With regular discharge	Outside of a meander bend
3	Glacial and fluvial deposit with the presence of some boulders	1.5	18	25°	With regular discharge	Straight
4	Glacial and fluvial deposit	1.7	19	37°	With regular discharge	Straight, after check dam

and depicted in Figure 3.

3. Methodology

3.1. State of the Art for Monitoring Bank Erosion

The conventional method used to measure erosion processes (in banks and hillslopes) is based on the use of erosion pins. This tool is characterized by a relatively low cost but provides only a punctual estimation of the erosion rate. Even if in literature there is an attempt to relate morphology activity rate (mm/year) through manual monitoring of erosion pins [39], the prediction and measurements of the erosion rate as well as the timing of its occurrence require alternative tools [12]. The increasing use of remote sensing in this field is promising.

Since the 1990s, close-range photogrammetry [40] has been increasingly applied to investigate fluvial processes (e.g., [41]) and has recently become a consolidated technique for the monitoring of erosion processes, such as ephemeral gully geometry measurement, stream bank erosion, and gully headcut evolution [42]. This is mainly due to the flexibility of the photogrammetric data acquisition, the low budget required for both hardware and software components, and the high degree of automation that has been reached in the image-based surface reconstruction process [43]. On the other hand, Scaioni et al. [44] discuss the problem of instantiating a stable reference system for the comparison and differencing of multi-temporal data sets. Some examples of application of close-range photogrammetry to measure riverbank retreat exist throughout literature [45,46,47,48,49,50]. Other research works assessed past riverbank erosion rates through aerial photographs [14,51,52,53,54,55], which feature the main advantage of covering a widely distributed area. However, there is a high degree of uncertainty in the estimated bank erosion rates based on aerial photograph analysis. First of all, the image scale may limit the acquisition of a sufficient resolution for the interpretation of results. Secondly, trees’ canopies may prevent the visibility of some riverbanks in the aerial photos. These problems might result in potential errors in the delineations of bank crests as well as the geo-rectification of aerial photographs [56].

Even satellite images are used for erosion estimation. Recently, automated mapping from satellite imagery has been applied for automatic identification of gullies based on ASTER imagery [57,58] and on IKONOS and GEOEYE-1 [59]. Airborne laser scanning (ALS) technique was applied for gully erosion estimates [60,61], for mapping riverbank elevations in flood management [62] and to assess bed erosion and sediment deposition [27,63]. ALS is capable of detecting global bank retreat, especially in lowland, but it is not able to detect local erosion phenomena since riverbanks are often sub-vertical. Some research papers have been published involving terrestrial laser scanning (TLS) for measuring erosion from streambanks and coastal cliffs at a relatively large scale as well as to detect spatial and temporal transformations in an entire river valley [24,25,64,65]. Lotsari et al. [30] investigated the interrelation between peakflow magnitude and duration, and the river morphodynamics. At the small scale, Rosser et al. [25] have noted the potential for using TLS for recording undercut banks and small-scale changes. Pizzuto et al. [19] analyzed the influence of trees on the erosion of a riparian zone through the use of a ground-based laser scanner and measurements of tree topography. Further, Leyland et al. [31] explored the link between bank roughness and erosion through multiple surveys using a combination of photogrammetry and TLS. Lyons et al. [18] conducted a survey on a bank of meandering portion of a stream, indicating the relationship between high intense precipitation events and destabilization by desiccation-cracking. The technique was successfully used to assess the adequacy of erosion protection measures (slump blocks) [66]. The usefulness of TLS for the analysis of morphological changes in varied scales has been reported by Heritage and Hetherington [26] as well as Kociuba et al. [24]. Moreover, appropriately filtered TLS data sets can provide remarkable information on bank morphology and on the spatial structure of bank retreat processes [67]. Milan et al. [27] applied high-resolution 3D laser scanning to a braided gravel-bed channel in the assessment of erosion and deposition volumes. The approach has advantages over total station [68], GPS [69,70] or a combination of both methodologies [71] due to the more rapid survey and increased point resolution. Resop and Hession [72] report that even if a total station is acceptably accurate for a single point measurement, an extrapolation of results would be heavily affected by errors, especially when dealing with complex topographies. On the other hand, TLS has the ability to quantify the spatial variability of retreat and advance over the entire streambank surface. Compared to aerial photogrammetry and ALS, which may cover larger areas, TLS shows greater spatial resolution and precision, and offers a better chance to survey vertical banks. Furthermore, data acquisition and processing are faster and simpler in comparison to close-range photogrammetry, which is nowadays capable of providing results similar to those achievable with TLS [43,73]. An important contribution is given by Resop and Hession [72]: the authors applied TLS for monitoring Stream Bank Retreat—a process affected by many different factors, including sub-aerial erosion processes, climate-related events, fluvial entrainment, direct transport of soil material by streamflow, and mass failure caused by bank instability. These investigations were conducted under different geological and climatic conditions compared to the ones in Tartano Valley.

Limitations to the applicability of TLS are associated with the inability to scan underwater topography as well as the difficulty to measure heavily vegetated surfaces [74], even though some instruments which are capable of recording multi-echo returns have been produced and applied. As well known, the laser beam features a growing divergence as far as it goes far from the sensor. The resulting footprint may easily partially penetrate the vegetation layer, but the most instruments can record only the first return corresponding to the outer surface. In the case of multi-echo acquisition, the ground surface beyond the vegetation layer could be sampled as well [75]. For the sake of completeness, some recent TLS instruments have started to scan the riverbed under shallow water as well. This option will be interesting to consider in future research.

An interesting work presented by Heritage and Hetherington [26] defines a protocol to ensure optimal surveying with TLS of river banks: a series of prescriptions are given about tool positioning and surveying design in order to maximize the point cloud quality and accuracy.

It is also important to highlight that most authors, which applied remote sensing to bank erosion, focused on lowlands basins. On the other hand, just few authors [27,76] published works related to mountain basins. Moreover, the majority of studies on the topic are based on long time intervals (usually yearly surveys) allowing the calculation of mobilized volumes but losing the link between the process and its triggering factors. In the literature, limited studies were conducted with more frequent surveys, for example Resop and Hession [72] who carried out six surveying sessions within two years.

3.2. Surveying Technique

The geometric survey was operated with a time-of-flight laser scanner Riegl LMS-Z420i (Figure 4). During each scanning campaign, a single scan station was established in each different location along the river. The choice of this elementary acquisition scheme was motivated by the need for rapid data acquisition, so that the four areas of interest could be entirely surveyed in less than a working day. The best practice protocol suggested by Heritage and Hetherington [26] was followed.

It should be mentioned that a preliminary data acquisition campaign was carried out with a phase-shift Faro Focus 3D close-range laser scanner. However, data captured by this instrument revealed several limitations, such as the lack of data for the weak response of wet soil and the long distance between the acquisition point and the object, which exceeded the maximum range of the instrument (approximately 25 m). An alternative solution for data acquisition could consist in the use of close-range photogrammetry, in particular in the application of the so-called “structure-from-motion (SfM)” technique [43,77]. The use of such approach is certainly very attractive for the survey of irregular objects without a predefined shape, such as the considered riverbanks. However, a fundamental requirement of the proposed application is the need of stable points to create a common reference system for data acquired at different epochs. Photogrammetry requires ground control points (GCP), visible in different images of the block, which means that a set of targets distributed on the considered riverbanks are necessary. The position of these points cannot be assumed as constant for the erosion and the progressive modification of the object.

For these reasons, the use of a time-of-flight laser scanner was the final choice. Data were acquired with an average density of 1 point/cm, which resulted in a point cloud composed by some million points per acquisition location. As data acquired at different epochs needed a common reference system to perform a multitemporal comparison, some special laser targets were placed on stable locations around each area of interest. Targets were fixed with a circular distribution around the scan location to ensure a reliable estimation of laser stand-points. One of the advantages of the adopted laser scanner, featuring a panoramic horizontal field-of-view (360°), is the opportunity to include targets that are not located on the eroded riverbanks, so that they can be assumed as being stable. Indeed, the application of close-range photogrammetry would require the positioning of targets visible in the images, i.e., to be installed on the riverbanks. Due to the inability of the adopted technique to penetrate water, the scanned areas are limited to the highest water surface level observed during the campaigns, which is later taken into account during the data processing phase.

Two kinds of targets were used: (1) 5 cm × 5 cm and 10 cm × 10 cm retro-reflective tapes; and (2) cylindrical targets on stable elements, such as railings, buildings, light poles and big rocks. In addition, these points were also measured with a Leica TS30 total station during the first measurement epoch, obtaining a set of 3D points that establish the reference system for registration of multitemporal laser scans. The use of the total station allowed one to define the vertical direction. This is mandatory for the Riegl LMS-Z420i, which does not have an internal sensor for the autonomous vertical alignment along the local plumb line.

Data registration was carried out with a six-parameter rigid-body transformation based on three rotations and three translations. A check based on standardized residuals was included in the least-squares estimation to remove gross errors, such as targets that had a displacement. After least-squares estimate of rigid-body transformation per any data set, a covariance matrix was estimated to account for the accuracy of geo-referencing stage along with the evaluation of the measurement uncertainty of the final digital surface model. The average sigma naught for computed least-squares regressions resulted as 5 mm.

Monitoring of the chosen banks has been carried out over the duration of one year, performing more surveys in a limited time span as opposed to previous studies reported in the literature. Few efforts were conducted with such temporal resolution and it was considered that only a more frequent sampling could provide information about the link between the process and its triggering factors. A high-frequency survey has been carried out by Milan et al. [27] however over a much shorter period (daily surveys spanning over 10 days) as well as by Lyons et al. [18] (nine surveys spanning over 19 months). Seven monitoring campaigns have been carried out from June 2014 to August 2015 (6 June 2014, 25 July 2014, 22 September 2014, 31 October 2014, 8 April 2015, 24 June 2015, and 5 August 2015). Although equally time spaced measurement sessions (one per month) had initially been planned, the limited accessibility to the monitoring sites and the impossibility to operate scanning during the snow cover period, resulted in some changes. For example, a gap between consecutive measurements from October 2014 to April 2015 could not be filled.

3.3. Data Post-Processing

The data obtained is characterized by surface distortion caused by irregular vegetation cover (e.g., grass, bushes) as shown on Figure 2. Even though the riverbank surfaces considered in this study were selected so as to avoid a significant presence of vegetation, some marginal green areas could not be avoided in laser scans. Therefore, some preliminary processing involved the manual removal of points associated with vegetation (similarly to Brasington et al. [70]). Automatic methods were not considered, as suggested in a previous study [78]). In fact, in TLS data the automatic filtering of vegetation is a more complex task than it is in ALS data, mainly due to the lack of multiple echoes.

A second important task consisted in the evaluation of the accuracy of 3D points. A rigorous approach to accomplish this task would require the analysis of each single point as well as the consideration of existing correlations between neighbor points. On the other hand, the implementation of a simpler methodology was pursued, which could be more practical to be repeated in other experiments. First of all the upper bound for the accuracy of 3D points has been evaluated, keeping into consideration that laser scans covered some areas of limited dimensions and no large discrepancies between accuracies should exist. The theoretical accuracy of 3D points was estimated by variance-covariance propagation of the following error sources [79].

1

Geo-referencing uncertainty, which has been evaluated by means of the estimated covariance matrix of rigid-body transformation.

2

Measurement errors on range and angles, as provided by the instrument constructor.

3

Effect of laser spot-size [80].

The estimated theoretical accuracy of 3D points was approximately ±1.5 cm in each spatial direction.

In order to calculate erosion and deposition volumes, the 3D point clouds were transformed into a grid Digital Elevation Models (DEM). Such a solution, widely used in scientific research [67,74] allows for the transformation of 3D clouds into 2D maps of elevation, making easier and faster the assessment of volumetric changes. Indeed, in the raw point clouds, point coordinates were defined in the topographic reference system established by ground control points. Since the erosion process in riverbanks is mainly oriented along the orthogonal direction with respect to the topographic surface, the use of such a reference system is not well suitable for the analysis of surface changes [81]. A 5 cm × 5 cm grid DEM was derived from each point cloud in order to transform point coordinates from the topographic reference system into another Cartesian reference system whose x-y plane is nearly parallel to the mean surface of the riverbank under consideration. Some mathematical details about this simple transformation can be found in Scaioni et al. [82]. The adopted resolution was retained as a sufficient tradeoff between the surface roughness, the point cloud spatial resolution (approximately 1 point every 1–2 cm), and the expected 3D point accuracy. On the one hand, this allows smoothing the effect of locally moving small rocks of a few centimeter diameter, whose displacements should not be confused with erosion/deposition. On the other hand, this DEM resolution preserves the shape of larger objects and the average riverbank surface, which both play a fundamental role in the multi-temporal analysis.

In order to select the most suitable interpolation method, the methodology proposed by Barbarella et al. [83] was followed. One data set per each case study was analyzed to this purpose. Using 99% of the points, four DEMs were interpolated by applying different algorithms (Nearest Neighbor, Natural Neighbor, Inverse Distance to a Power—2nd degree, and Kriging—linear variogram). In order to evaluate the coherence of the DEM interpolated surface with respect to the input point cloud, the height difference between the remaining 1% laser points and the interpolated surface in the corresponding positions were considered. A set of statistical parameters were analyzed in the interest of making a decision on the interpolation technique to be extensively adopted. Generally, the different algorithms performed in very similar manner and thus, the Natural Neighbor was chosen due to the simpler computation and the independence from control parameters. This result turned out to be quite different from what has been reported by other authors. For example, Schwendel et al. [84] argue that very large discrepancies can be obtained from the application of different interpolators, although the initial point density in the data set they adopted was rather scarce. In fact, in that study a set of RTK-GPS points was used. When using TLS data, the spatial resolution of the raw point cloud used as input for the interpolation is generally much denser. This results in a better sampling of the topographic surface and the output is less dependent upon the interpolation method.

The DEM maps were created for each bank per each surveying campaign. A total number of 28 maps were available. In practice, this task was carried out using Golden Software Surfer^®.

The theoretical accuracy of the DEM was estimated by propagating the variance-covariance matrix of single points through the transformation into the new reference system and by considering the resampling process into the new grid. This led to a theoretical accuracy of height points in the DEM of approximately ±1.8 cm.

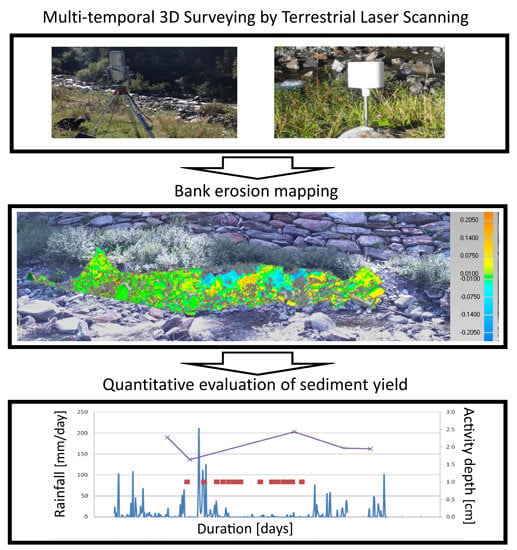
After the DEM models have been obtained, they have been used to analyze the erosion process at the four banks. In order to detect the erosive activity, the difference between consecutive DEMs, called DEM of Difference (DoD) was used to highlight and present the locations in which erosion or deposition occurred (indicated by a color scale). So as to represent the erosion variation in a consistent manner, it has been expressed as activity depth or in other terms—the ratio of volume of displaced material to the surface area of the bank [74].

Certainly, the uncertainty of a single epoch DEM also propagates into the DoD. The evaluation of single cell uncertainty of the DoD resulted in ±2.5 cm. As demonstrated in a previous work [82], this uncertainty can be retained as a largely safe value, since neglecting correlations among adjacent points leads to overestimation of single point accuracy up to a factor of 50%.

4. Results

The pattern of erosion and deposition has been retrieved from the DoD values, where the sum of all negative change cells is erosion and the sum of all positive change cells is deposition. The volume obtained from the surveyed riverbanks during corresponding periods is summed up in Figure 5.

The results of the analysis are presented in Figure 6, Figure 7, Figure 8 and Figure 9, where erosion and deposition depths are collected along with relevant meteorological conditions, namely rainfalls and air temperature retrieved by a weather station located nearby.

In Figure 6, Figure 7, Figure 8 and Figure 9, histograms are also reported showing how the frequency of DoD is distributed. Each vertical bar represents a class spanning over a 2 cm variation. The histograms also display the thresholds of ±2 σ (5 cm), where σ = 2.5 cm is the estimated standard deviation of the DoD map. These thresholds can be used for discriminating the noise due to the geo-referencing, measurement, and interpolation process, from statistically significant changes. As it can be seen in all maps displaying computed DoD values, both positive and negative changes are clustered in hot spots. The values of such spots are, for the most part, outside the central band confined by the thresholds of ±2 σ, which should contain points that are completely masked by measurement noise with a risk probability of 5%. This results in the fact that the outcome of the following analysis, based on computed DoD, can be retained as meaningful. On the other hand, hot spots are interspaced by areas characterized by very small changes, which cannot be distinguished from the uncertainty of the DoD map. Undoubtedly, when computing the global statistics of erosion/deposition areas, the single point uncertainty is improved by considering the large number of samples that are averaged. In fact, another option to analyze changes in the DoD map is not to consider single point-by-point differences, but to compute differences over sampling windows. This method can reduce the effect of measurement noise, but will also smoothen the results.

Bank 1 (Figure 6), characterized by a high rise and an almost vertical slope does not show a clear peak in erosion over the monitoring period. Epoch A shows the presence of scattered erosion at the higher parts of the bank as well as some deposition spots at the lower sections, which might have possibly formed as a consequence. A similar result can be observed in Epoch B, in which no significant variation in the erosive activity can be detected. Although the obtained measurements indicate the presence of erosive activity, concentrated at a specific point of the bank, its magnitude seems unlikely and is therefore assumed to be the result of anthropogenic activity, which was noticed during the monitoring campaigns. Due to the high rise of the bank, the water stream is rarely in contact with the surface area and therefore no basal erosion can be noticed (Table 1). In addition, the observed limited erosion rate can be explained with the position of the bank—immediately after a narrow portion of the river that partially protects it from direct flow impact (Figure 3). The almost vertical slope of the bank suggests that the scattered nature of the observed erosion/deposition patterns can be related to mechanical instability instead of fluvial activity. These instabilities are probably due to seasonal freeze-thaw cycles, which significantly influenced the bank material creating erosional and depositional spots.

Bank 2 is affected by the river discharge (Table 1, Figure 3) and therefore concentrated variations of erosion can be observed at the toe, where water often reaches the bank surface. This effect can be explicitly observed in the difference between consecutive measurements in Epochs A and B. The elevated precipitation rate during the autumn and early winter of 2014 accounts for the increased erosive activity of the river stream. In addition, the position of Bank 2 on the outside of a meander bend favors the erosive power of shear forces exerted on the surface by the stream. In this case, the observed toe erosion is an indication for the influence of fluvial activity, conversely to Bank 1. A strong peak in the erosive activity can be observed in the measurement taken during the spring season (Epoch B). This effect can be explained with the coupled action of several triggering processes related to the seasonal change. In addition to the fluvial activity, Bank 2 is subject to direct rainfall impact as well as snowmelt, since the bank is characterized by a mild steepness (Table 1). Moreover, many authors published works, in which they link the compromised strength of the shallow layers of the soil during and after freeze-thaw cycles, and an acceleration in erosion processes due to the presence of excessive soil water from melted ground ice [85,86,87,88,89]. It has been noted that boulders of larger size remain static since the slope of this bank is not characterized by such a severe steepness, and therefore the destabilizing action of gravity is reduced. The clearly visible extensive erosion pattern at the toe of the bank indicates that it has been affected by the water stream. Therefore, it can be argued that the erosive activity at Bank 2 is not affected by mechanical instability as in the case of Bank 1, but instead, phenomena related to seasonal variation as well as fluvial activity are responsible for the bank erosion. It is also worth noting that the amount of eroded material from Bank 2 (3.75 cm) is more than twice the one of Bank 1 (1.5 cm).

Banks 3 and 4 show patterns of temporal variability of the erosion activity similar to the results of Bank 2. Despite the different magnitude, a distinct peak exists in both cases (Epoch B), which confirms that increased bank erosion rates are closely related to high precipitation levels and freeze-thaw cycles. The erosion/deposition patterns of Bank 3 highlight the effect of the fluvial action on the stability of the bank near the flow. The displacement of even big boulders can be noticed in the downstream direction. On the other hand, Bank 4 is characterized by a highly distributed erosive activity along the extension of the monitored surface. Both banks are affected by the action of the river flow as well as the destabilizing effect of the freeze-thaw cycles, although the magnitude of the erosion activity is considerably less than in the case of Bank 2.

5. Discussion

A preliminary classification of the monitored riverbanks on the basis of their erosive activity groups Banks 2, 3, and 4 together. Bank 1 shows a different behavior, which suggests that the processes involving erosion are different with respect to the other test banks. This division reflects the difference in terms of geometry, since Bank 1 is the only sub-vertical high slope, while the others are less steep and of lower elevation. Moreover, due to the geometric features of the banks (Table 1), the regular flow discharge of the river is able to affect a larger portion of the bank surface when it is in contact with the flow. It can be argued that the kinematics of the process are different in the two cases. While Banks 2, 3 and 4 are predominantly affected by fluvial activity, the kinematics of Bank 1 suggests that the activity here is the result of sub-aerial erosion processes. Furthermore, it is worth noting that the position of the bank relative to the water stream as well as its geometrical features play an important role in its erosive behavior.

The monitored surfaces exhibit a clear relationship between erosive activity and consequences of the main seasonal change (increased precipitation and freeze-thaw cycles). Although the erosive activity of Bank 1 is not characterized by a clear peak in the spring season, the activation of erosive processes during this period can be observed considering the presence of some erosion and deposition spots (Figure 6—“Change map” A Bank 1). On the other hand, the rest of the monitored surfaces exhibit peaks of bank erosion during the spring season, which is related to intense rainfall and snowmelt. This effect has been widely discussed and therefore, the obtained results confirm its validity. In addition, the increased mean temperature provokes the thawing of the frozen shallow soil layers, which reduces the soil strength and therefore, loosens the surface and makes it susceptible to the different erosive agents [90].

The real challenge in the study of riverbank erosion deals with the definition of the contribution of each geomorphic process. Considering that a long term monitoring is of paramount importance to really comprehend the bank behavior and consequently the sediment production, only a simple attempt to extrapolate a potential total volume from the information gathered in the measurement campaigns is hereby presented, without any claim to be exhaustive. In fact, it has to be considered that data collected through one year are strongly influenced by the climate and rainfall conditions and cannot be considered as representative of the general mean contribution of the riverbank to the total sediment yield. Moreover, a detailed geomorphic analysis of all the streams’ banks should be carried out in order to improve the extrapolation of results. However, a rough estimation of the total bank erosion along the stream is presented to get an approximate idea of the significance of this process relative to the various sediment-producing processes. It is worth pointing out that the year during which the analysis was carried out (May 2014–October 2015) was characterized by regular rainfalls, with a total precipitation rate slightly over the annual mean but without extreme events, which could evolve into floods or cause any damage, even when daily rainfalls show peaks of over 100 mm. The total amount of sediment released by erosion inside the stream is estimated by simply multiplying the volumetric erosion per linear meter of surveyed bank by the total length of the river: choosing the two extreme banks (least and most productive) the result ranges between 4500 m³/year. and 8000 m³/year. The volume obtained ranges from 11.8% to 21% of the mean yearly siltation in the Campo dam, which is considered a reasonable value according to Thoma et al. [12] and De Rose and Basher [14]. Therefore, it is evident that bank erosion cannot be considered a secondary process and deserves deeper studies.

The application of terrestrial laser scanning has revealed to be a key-point of this research, since it was able to provide point clouds useful for identifying the areas of retreat and advance of the riverbank. This type of spatial information is crucial for the understanding of the overall kinematic behavior of the studied area. The density of laser scanning point clouds offered observations much more complete with respect to traditional pin-based measurements, which are able to furnish only point-wise data and interfere directly with the monitored surface. On the other hand, the accuracy of the 3D point cloud data was more than sufficient to understand the erosion process, since the total amount of measurement, interpolation and geo-referencing errors resulted in a threshold for discriminating significant changes in the DoD maps that could be estimated to be 5 cm (2σ). Another significant advantage associated with the use of TLS is the opportunity to collect 3D data on sub-vertical and vertical slopes (as in the case of Bank 1) making this method rather flexible when dealing with complex riverbank morphologies.

On the other hand, there are still several limitations associated with this technique. Station set up and geo-referencing require additional time with respect to data acquisition itself and the analysis of large data sets can be extensively time consuming. Further limitations include the inability of the scanner to penetrate water as well as to differentiate vegetation, which would require data post processing. In this respect, an alternative can be found by adopting proper hardware solutions, i.e., TLS sensors capable of multi-echoing as well as the ones able to scan below shallow waters (see Section 3.1). Moreover, in order to increase the spatial distribution of the measurements, a high number of scans would be required (e.g., 86 sites in a valley [24]). Therefore, in order to cope with these issues, TLS has often been employed in combination with other techniques. A possible solution has been proposed in Vaaja et al. [91] and Hackney et al. [66], who employed a mobile laser scanning (MLS) system to map changes (erosion/deposition) in riverine topography. In case the MLS sensor is installed on a car, only vehicle-accessible sites are suitable for the application of this technology. This certainly represents a strong limitation in mountain areas. An interesting alternative is given by the use of MLS sensors on more flexible platforms such as boats [66], Unmanned Aerial Vehicle (UAV), and backpacks [92]. Generally, if high quality positioning sensors (Global Navigation Satellite System (GNSS) and inertial measurement unit) are adopted and operated in proper conditions, the accuracy and spatial resolution offered by MLS is only slightly worse with respect to the one provided by static laser scanning. Proper conditions mainly refer to a sufficient sky-visibility in order to enable good-quality GNSS positioning. In addition, the spatial distribution of measurement data can be improved by means of airborne laser scanning (ALS). In the work of Bremer and Sass [93] both methods were combined in order to exploit the area-wide applicability of ALS and the flexible acquisition of TLS to quantify the sediment volume transported by a major debris flow event in the Halltal, Austrian Alps.

The equipment cost is considered a major drawback of the laser scanning technology. An interesting alternative, as already mentioned in this paper, is given by the so-called Structure-from-Motion (SfM) photogrammetry [43], which could potentially provide data sets similar to the ones achievable by TLS by means of cheaper and more flexible equipment. On the other hand, the application of photogrammetry suffers from the need of GCPs positioned in the area covered by the images. Conversely, in order to obtain a stable reference system (see [26]) TLS requires GCPs, which can be even outside of the scanned area. An alternative to the use of GCPs is given by the application of methods for comparing surfaces based on 3D matching algorithms [94]. In addition, in such a case, the presence of areas that may have undergone dramatic changes between the observation epochs may prevent the use of surface-based comparison, for example, due to the presence of vegetated and weathered areas. However, it should be pointed out that the technological development of TLS technology develops with the implementation of smaller and much faster sensors, in some cases integrating theodolite and scanning capabilities.

Due to the considerable level of uncertainty in the actual amount of erosion, the temporal scale and resolution of the monitoring process should be increased in order to obtain long-term and more detailed data. Observation of longer periods (e.g., several years) as well as of higher frequency, would enable a more precise estimation of the amount of bank erosion. In addition, such a spatial variability, even in small basins, would result in highly vague outcomes when extrapolated over the entire basin. Therefore, an improvement of the current work will be pursued, using the available technology, in order to better describe and quantify the problem of bank erosion in Tartano Valley. Additionally, improvements in volume estimation for our case study are certainly possible but require further research. As a first step, an accurate geomorphic survey and mapping could help in dividing the banks into homogeneous groups. After this mapping is achieved, one or more test sites for each kind of bank should be selected in order to estimate different erosion rates for several conditions. The use of TLS could support the survey of the banks, as it has been done for the four presented cases, but it is essential to take into account a larger time span (e.g., several years). Finally, a measure of water flow or water level inside the river can be useful to better comprehend the different role of river discharge and rainfall (runoff on the bank, role of drops, and the increase of groundwater level as well).

6. Conclusions

The overall aim of this research was to investigate the riverbank erosion in Tartano Valley in order to address three main issues linked with this process. They can be summarized as “how” (the general kinematic behavior of the riverbank), “when” (the influence of seasonal features on river bank erosion), and “how much” (the role of riverbank erosion in sediment yield).

The high temporal resolution of monitoring (more surveys over one year) represents a novelty in this field and allows for the better understanding of the erosion processes in terms of their predisposing and triggering factors. The analysis of the collected data has been carried out by creating a set of digital elevation models from terrestrial laser scanning point clouds and comparing them in a pair-wise manner, epoch by epoch, in order to detect changes. Four graphs summarize the erosion and deposition information along with recorded rainfall depth and freeze-thaw cycles (see Figure 6, Figure 7, Figure 8 and Figure 9).

The data collected document significant indications of the riverbanks’ kinematic behavior. First of all, the position of the bank relative to the water stream as well as its geometrical features are crucial factors that favor the occurrence of erosion. As a matter of fact, it is possible to state that when there is a contact between a bank and the river, the former is predominantly affected by fluvial activity. Instead, if interaction occurs only during an exceptional river discharge, the bank kinematic is generally ruled by sub-aerial erosion processes.

For what concerns the relationship between riverbank erosion and seasonal features, as also confirmed by other works, a peak in erosion activity is evident in the spring season. The peak is clearly present for Banks 2, 3 and 4. Instead, Bank 1, which is different in terms of predisposing factors (see Table 1), does not show a peak, although some erosion and deposition spots (Figure 6—“Change map” A Bank 1) are present. Finally, an attempt to quantify the total amount of material eroded from banks was presented aiming to understand the contribution of riverbank erosion in sediment supply. Due to the uncertainty in estimation as well as the need of long term measurements (possibly in the span of several years), only a rough evaluation of the potential total volume was accomplished. The volume obtained varies in the range 10%–20% of the total sediment yield of the basin.

In conclusion, the outcome of this work underlines the importance of riverbank erosion for the dynamics of the river basin as well as for its off-site consequences. Observation of longer periods as well as higher frequency using available technology, would undoubtedly improve the knowledge on this topic. Moreover, an accurate geomorphic survey would provide further valuable information, useful for the better comprehension of the contribution of this process to the sediment yield of the river basin.