Frescoed Vaults: Accuracy Controlled Simplified Methodology for Planar Development of Three-Dimensional Textured Models
Abstract
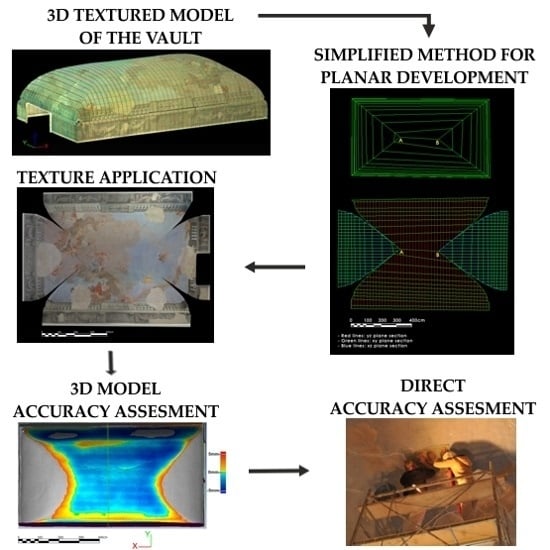
:1. Introduction
2. State of the Art
2.1. Geometry Survey
2.2. Texture Mapping
2.3. Vault Development
3. Materials and Methods
3.1. The Case Study
3.2. 3D Modeling and Texturing
3.3. Vault Development
3.3.1. Analysis and Preliminary Processing of Laser Data
3.3.2. Analysis of the Development Methodology
- Image pairs and the geometric vault development frame (Figure 8) have been imported in the same photo editing software environment.
- A single block has been created with both images, so that any transformation applied to any one image was similarly applied to the other.
- The layer containing the image with just the texture has been turned off, leaving visible just the image with the section lines.
- The image has been scaled and moved on the geometric frame, assuming the section lines obtained with XZ and YZ planes (vertical lines in Figure 10) as reference.
4. Results and Discussion
4.1. Assessment of Model Geometrical Accuracy
4.2. Texture Dimension and Positioning Accuracy Assessment
4.3. Vault Development Accuracy Assessment
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dequal, S. An unconventional application of analytical plotters to architectural photogrammetry: Projection, plotting and digitizing on non plane surfaces. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 1988, 27, 140–146. [Google Scholar]
- Karras, G.E.; Petsa, E.; Dimarogona, A.; Kouroupis, S. Photo-textured rendering of developable surfaces in architectural photogrammetry. In Virtual and Augmented Architecture (VAA’01); Springer: London, UK, 2001; pp. 147–158. [Google Scholar]
- Karras, G.E.; Patias, P.; Petsa, E. Digital monoplotting and photo-unwrapping of developable surfaces in architectural photogrammetry. Int. Arch. Photogramm. Remote Sens. 1996, 31, 290–294. [Google Scholar]
- Georgopoulos, A.; Makris, G.N.; Tournas, E.; Ioannidis, C.H. Digitally developing works of art. In Proceedings of the CIPA 2001 International Symposium, Potsdam, Germany, 18–21 September 2001.
- Valanis, A. Fitting, portrayal and mapping for the production of 2nd order surfaces photomosaics. Int. Arch. Photogramm. Remote Sens. 2002, 34, 463–467. [Google Scholar]
- Lerma, J.L.; Tortosa, R.V. Digital development of a small Valencian tower. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 451–454. [Google Scholar]
- Pera, L. Tecnica Dell’architettura. Tipologia Strutturale; Goliardica: Pisa, Italy, 1987. [Google Scholar]
- De la Plaza Escudero, L. Diccionario Visual de Términos Arquitectónicos; Grandes Temas Cátedra: Madrid, Spain, 2008. [Google Scholar]
- Lerma, J.L.; Pérez, C. 3D Photorealistic and interactive reconstruction of covered up frescoes. In Recording, Modeling and Visualization of Cultural Heritage; Baltasavias, E., Gruen, A., Van Gool, L., Pateraki, M., Eds.; Taylor & Francis Group: London, UK, 2006; pp. 485–491. [Google Scholar]
- Bevilacqua, M.G.; Caroti, G.; Piemonte, A. Rilievi integrati della Basilica romanica di San Gavino a Porto Torres. In Proceedings of the 16a Conferenza Nazionale ASITA, Vicenza, Italy, 6–9 November 2012; pp. 391–396.
- Caroti, G.; Piemonte, A. An integrated survey for knowledge and preservation of a cultural heritage: The Albanian fortified citadel of Elbasan. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 373–378. [Google Scholar]
- Caroti, G.; Piemonte, A. Studio relativo al rilevamento di dettaglio di una porzione del transetto nord della chiesa di San Paolo a Ripa d’Arno al fine di procedere al consolidamento strutturale. In Proceedings of the Un incontro informale per i 70 anni del Prof. Carlo Monti, Milano, Italy, 3 May 2012; pp. 1–6.
- Dore, C.; Murphy, M. Integration of Historic Building Information Modelling (HBIM) and 3D GIS for recording and managing cultural heritage sites. In Proceedings of the IEEE 18th International Conference on Virtual Systems and Multimedia (VSMM), Milan, Italia, 2–5 September 2012; pp. 369–376.
- Juan Vidal, F.; Martínez-Espejo Zaragoza, I. Hypotesisforthe virtual anastilosis of themainchapel of the Iglesia de Los Desamparados de Les Coves de Vinromá. In Proceedings of the 16th International Conference on Cultural Heritage and New Technologies, Vienna, Austria, 14–16 November 2011; pp. 201–212.
- Lerma, J.L.; Cabrelles, M.; Navarro, S.; Seguí, A.E. La documentación patrimonial mediante sensores de imagen o de barrido láser. In Documentación Gráfica del Patrimonio; Ministerio de Cultura: Madrid, Spain, 2011; pp. 108–117. [Google Scholar]
- Marambio, A.; Pucci, B.; Nuñez, M.A.; Buill, F. La aplicación del escáner láser terrestre en la catalogación del patrimonio arquitectónico del casco histórico de Castellfollit de la Roca. In Proceedings of the VIII Semana Geomática Internacional, Barcelona, Spain, 3–5 March 2009; pp. 1–8.
- Martínez-Espejo Zaragoza, I.; Juan Vidal, F. Gestión gráfica avanzada de edificaciones antiguas. In Proceedings of the XI Congreso Internacional de Expresión Gráfica Aplicada a la Edificación, Universidad Politécnica de Valencia, Valencia, Spain, 29 November–1 December 2012; pp. 710–714.
- Alsadik, B.; Remondino, F.; Menna, F.; Gerke, M.; Vosselman, G. Robust extraction of image correspondences exploiting the image scene geometry and approximate camera orientation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 40, 1–7. [Google Scholar] [CrossRef]
- Guidi, G.; Russo, M.; Beraldin, J.A. Acquisizione 3D e Modellazione Poligonale; McGraw-Hill: Milano, Italy, 2010. [Google Scholar]
- Guidi, G.; Remondino, F. 3D Modelling from real data. In Modelling and Simulation in Engineering; Catalin Alexandru, C., Ed.; InTech: Vienna, Austria, 2012; pp. 69–102. [Google Scholar]
- Koska, B.; Křemen, T. The combination of laser scanning and structure from motion technology for creation of accurate exterior and interior orthophotos of St. Nicholas Baroque church. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 40, 133–138. [Google Scholar] [CrossRef]
- Lerma, J.L.; Navarro, S.; Cabrelles, M.; Villaverde, V. Terrestrial laser scanning and close range photogrammetry for 3D archaeological documentation: The upper Palaeolithic Cave of Parpalló as a case study. J. Archaeol. Sci. 2010, 37, 499–507. [Google Scholar] [CrossRef]
- Wenzel, K.; Rothermel, M.; Fritsch, D.; Haala, N. Image acquisition and model selection for multi-view stereo. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 40, 251–258. [Google Scholar] [CrossRef]
- Remondino, F.; Spera, M.G.; Nocerino, E.; Menna, F.; Nex, F. State of the art in high density image matching. Photogramm. Rec. 2014, 29, 144–166. [Google Scholar] [CrossRef]
- Apollonio, F.I.; Ballabeni, A.; Gaiani, M.; Remondino, F. Evaluation of feature-based methods for automated network orientation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 47–54. [Google Scholar] [CrossRef]
- Caroti, G.; Martínez-Espejo Zaragoza, I.; Piemonte, A. Accuracy assessment in structure from motion 3D reconstruction from UAV-born images: The influence of the data processing methods. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 103–109. [Google Scholar] [CrossRef]
- Apollonio, F.I.; Remondino, F. Modellazione 3D da sensori attivi Pipeline con laser scanner. In Modelli Digitali 3D in Archeologia: Il Caso di Pompei; Scuola Normale Superiore Pisa: Pisa, Italy, 2010; pp. 94–117. [Google Scholar]
- Carpiceci, M. Survey problems and representation of architectural painted surfaces. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, 523–528. [Google Scholar] [CrossRef]
- Menna, F.; Rizzi, A.; Nocerino, E.; Remondino, F.; Gruen, A. High resolution 3D modeling of the behaim globe. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 115–120. [Google Scholar] [CrossRef]
- Cipriani, L.; Fantini, F.; Bertacchi, S. Survey and representation of vaults and cupolas: An overview on some relevant Italian UNESCO Sites. In Proceedings of the IEEE International Conference on Virtual Systems & Multimedia (VSMM), Hong Kong, China, 9–12 December 2014; pp. 50–57.
- Chiabrando, F.; Rinaudo, F. Recovering a collapsed medieval fresco by using 3D modeling techniques. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 105–112. [Google Scholar]
- Pancani, G. Lo svolgimento in vera grandezza delle volte affrescate delle sale dei quartieri al piano terreno di Palazzo Pitti a Firenze. In Proceedings of the Giornate di Studio Il Disegno delle trasformazioni, Napoli, Italy, 1–2 December 2011; pp. 1–11.
- Cannella, M. Sviluppo e Rappresentazione Digitale di Superfici Architettoniche Complesse per la Documentazione e il Restauro. Available online: http://hdl.handle.net/10447/130394 (accessed on 25 November 2015).
- Meyer, E.; Parisel, C.; Grussenmeyer, P.; Revez, J.; Tidafi, T. A computerized solution for the epigraphic survey in Egyptian Temples. J. Archaeol. Sci. 2006, 33, 1605–1616. [Google Scholar] [CrossRef]



















| Area 1 | Area 2 | |
|---|---|---|
| Radius (m) | 7.349 | 5.280 |
| STDV (m) | 0.007 | 0.008 |
| X | Y | Z | |
|---|---|---|---|
| mean (m) | 0.000 | 0.000 | 0.000 |
| max (m) | 0.005 | 0.005 | 0.010 |
| STDV (m) | 0.002 | 0.003 | 0.004 |
| X | Y | Z | |
|---|---|---|---|
| mean (m) | 0.000 | 0.000 | 0.000 |
| max (m) | 0.019 | 0.023 | 0.026 |
| STDV (m) | 0.007 | 0.007 | 0.008 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bevilacqua, M.G.; Caroti, G.; Martínez-Espejo Zaragoza, I.; Piemonte, A. Frescoed Vaults: Accuracy Controlled Simplified Methodology for Planar Development of Three-Dimensional Textured Models. Remote Sens. 2016, 8, 239. https://doi.org/10.3390/rs8030239
Bevilacqua MG, Caroti G, Martínez-Espejo Zaragoza I, Piemonte A. Frescoed Vaults: Accuracy Controlled Simplified Methodology for Planar Development of Three-Dimensional Textured Models. Remote Sensing. 2016; 8(3):239. https://doi.org/10.3390/rs8030239
Chicago/Turabian StyleBevilacqua, Marco Giorgio, Gabriella Caroti, Isabel Martínez-Espejo Zaragoza, and Andrea Piemonte. 2016. "Frescoed Vaults: Accuracy Controlled Simplified Methodology for Planar Development of Three-Dimensional Textured Models" Remote Sensing 8, no. 3: 239. https://doi.org/10.3390/rs8030239
APA StyleBevilacqua, M. G., Caroti, G., Martínez-Espejo Zaragoza, I., & Piemonte, A. (2016). Frescoed Vaults: Accuracy Controlled Simplified Methodology for Planar Development of Three-Dimensional Textured Models. Remote Sensing, 8(3), 239. https://doi.org/10.3390/rs8030239