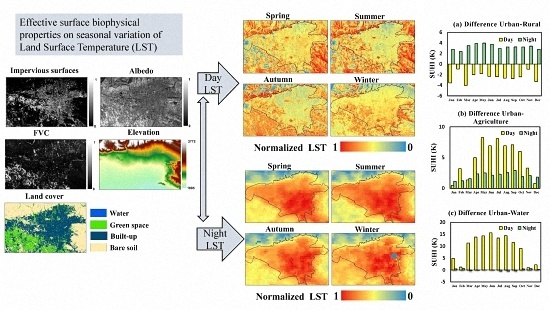
Seasonal Variations of the Surface Urban Heat Island in a Semi-Arid City

Abstract

The process of the surface urban heat island (SUHI) varies with latitude, climate, topography and meteorological conditions. This study investigated the seasonal variability of SUHI in the Tehran metropolitan area, Iran, with respect to selected surface biophysical variables. Terra Moderate Resolution Imaging Spectroradiometer (MODIS) Land Surface Temperature (LST) was retrieved as nighttime LST data, while daytime LST was retrieved from Landsat 8 Thermal Infrared Sensor (TIRS) using the split-window algorithm. Both data covered the time period from September 2013 to September 2015. To assess SUHI intensity, we employed three SUHI indicators, i.e., the LST difference of urban-rural, that of urban-agriculture and that of urban-water. Physical and biophysical surface variables, including land use and land cover (LULC), elevation, impervious surface (IS), fractional vegetation cover (FVC) and albedo, were selected to estimate the relationship between LST seasonal variability and the surface properties. Results show that an inversion of the SUHI phenomenon (i.e., surface urban cool island) existed at daytime with the maximal value of urban-rural LST difference of −4 K in March; whereas the maximal value of SUHI at nighttime yielded 3.9 K in May. When using the indicators of urban-agriculture and urban-water LST differences, the maximal value of SUHI was found to be 8.2 K and 15.5 K, respectively. Both results were observed at daytime, suggesting the role of bare soils in the inversion of the SUHI phenomenon with the urban-rural indicator. Maximal correlation was observed in the relationship between night LST and elevation in spring (coefficient: −0.76), night LST and IS in spring (0.60), night LST and albedo in winter (−0.53) and day LST with fractional vegetation cover in summer (−0.41). The relationship between all surface properties with LST possessed large seasonal variations, and thus, using these relationships for SUHI modeling may not be effective. The only exception existed in the correlation between elevation and IS, which may be useful to simulate the SUHI at night. This study suggests that in semi-arid cities, such as Tehran, with the urban-rural indicator, a surface urban cool island may be observed in daytime while SUHI at nighttime; with other indicators, SUHI can be observed in both day and night. Thus, SUHI studies require the acquisition of remote sensing image data at both daytime and nighttime and careful selection of SUHI indicators.

1. Introduction

The urban heat island (UHI) is a well-known effect of urbanization, a phenomenon whereby urban areas experience higher temperature than the surrounding rural areas [1]. Replacing natural land cover with pavement, buildings, concrete, asphalt and other urban constructions changes the surface energy balance [2]. In addition, vehicles, factories and air conditioning units increase peripheral heat. Further, tall buildings and narrow streets reduce air flow [3]. The adverse effects of UHI include: (1) increasing thermal discomfort; UHI will increase the duration and the degree of thermal discomfort [4]; (2) increase in energy consumption [5]; a temperature rise of 20 °C to 25 °C created a 5% to 10% increase in demand for electricity [6]; (3) air pollution; UHI increased the production of ozone near the ground [7] and, in the form of mesoscale wind, dispersed air pollution [8]; (4) reducing water quality; rapid temperature changes in the water ecosystems caused by surface runoff from hot pavements and roofs covered with asphalt, mostly stressful and fatal for aquatic life [9]; and (5) increase in per capita water consumption in summer time [10]. This will increase the need for more irrigation of green cover due to increased evapotranspiration [11]. From the first evidence of the urban heat island, various strategies have been developed to create cool urban surfaces by increasing vegetation cover, using reflective roofs and walls, green roofs and cool floors [12]. Along with the urban population increase, construction of more comfortable urban places and the energy consumption concern, the UHI issue has been of great importance in society today. Likewise, with the concern of global warming, the UHI issue will be more complicated in the future [13,14].

The thermal property is a key component of the urban surface energy balance and directly affects the air temperature above it [15]. Surface urban heat islands (SUHIs) exist at any time of the day and are more intense near mid-day during the summer [16]. SUHI plays an important role in the thermal characteristics of urban layers above the ground. The source of nighttime radiant heat mainly comes from stored heat during the daytime and anthropogenic objects. The use of remote sensing techniques is the most common method for the analysis of land surface temperature (LST) and SUHI [17]. A set of satellite sensors for acquiring thermal infrared (TIR) data from the Earth’s surface have been employed, and the SUHI effect has been studied with different TIR data with a variety of resolutions [18]. Several studies have focused on the relationship between LST and land use/cover [19,20] and the urban surface biophysical composition [21,22]; while the UHI spatial-temporal variations had been studied in connection with the increase in urbanization level and land use/cover changes [23,24,25]. Some authors had studied the means to reduce the SUHI effect and to apply strategies to decrease the SUHI effect [14,26]. Although vegetation cover has often found strong negative correlation with LST [27], Mackey et al. [14] showed that among the SUHI strategies in Chicago, typical instances of efforts to increase albedo, such as reflective roofs, generated a stronger cooling effect than common instances of NDVI efforts, such as green roofs, street trees and green spaces.

Although the development of UHIs and SUHIs is generally associated with urban sprawl and increasing industrial and human activities, the geographical location, climatic situation, urban materials, seasons and times of day and night can generate different effects. Lazzarini et al. [28] studied the SUHI in Abu Dhabi, a desert city. Their results showed an inversion of the normal SUHI phenomenon in daytime, where the downtown areas appeared cooler compared to the suburbs with a daily difference of 5 to 6 K in summer and 2 to 3 K in winter. Ganbat et al. [29] observed high seasonal variation (i.e., 3.3 K in winter and 0.3 K in summer) in Ulaanbaatar, the capital city of Mongolia, a semi-arid metropolitan are. Their results also showed that the strongest daily maximal UHI intensity occurred in winter with an average intensity of 6.4 K, and the weakest cases occur in summer with an average intensity of 2.5 K. The frequency of occurrence on the diurnal maximum of UHI intensity in the nighttime was 5.6-times higher than the daytime. Schwarz et al. [30] studied the UHI of 263 European cities with monthly mean temperatures by using MODIS data products and different UHI indicators. They found that differentiating cities into various thermal climate zones increased the correlation with the selected indicators.

In recent decades, Tehran has been experiencing environmental problems, such as UHI [31,32,33] and urban air pollution (UAP) [34,35] that has impacted the health and even endangered the lives of local residents. UHI and UAP have a common source and interact with each other [4,8]. Horizontal and vertical urban expansion without careful planning in Tehran has caused the reduction of local winds to move away urban pollutants. In such a circumstance, SUHI, through impacts on the urban boundary layer (UBL), became an important factor in the density and dispersion of urban pollutants. These phenomena directly or indirectly affect the water and electricity consumption on warm days, impacting human comfort, public health and quality of life. Therefore, it is necessary to monitor SUHI. The aim of this study is to assess the seasonal variations of LST and SUHI and to find the relationship between SUHI and urban surface biophysical variables in Tehran.

2. Study Area and Data

2.1. Study Area

The selected study area (Figure 1) is Tehran, capital of Iran, a city with a population of almost 12.5 million. The city center is located at 34.41°N and 51.25°E on the south slope of the Alborz mountain range on an alluvial fan. Tehran is limited by the mountains to the north and the east, which strongly affect the city’s climate. This area is on the subtropical high pressure belt during the summer, which makes it warm and dry. The Alborz Mountains partially reduce the area of dryness. The city has a relatively irregular urban pattern, and the per capita green space is less than standard. The world average is 20 to 25 sq·m per person, while Tehran is 4.5 sq·m. per person. In addition, the distribution of green spaces in the city is heterogeneous. The biophysical settings are closely related to environmental problems, such as UHI and air pollution. The monitoring of spatial and temporal patterns of UHI allows the assessment of heat-related health risks and proposing measures to reduce adverse UHI effects. Figure 1 illustrates the urban, agriculture, industrial and water area. Urban area includes industrial area, while rural area includes agriculture area.

2.2. Data Sources

We used MOD11_A2, Terra MODIS LST eight-day data and the Landsat-8 Operational Land Imager (OLI) and TIRS, from September 2013 to September 2015. MODIS is aboard the Terra (originally known as Earth Observing System Ante Meridiem (EOS AM-1)) satellite, launched in December 1999. It acquires data in 36 spectral bands with a passing time over the Equator around 10:30 a.m. and 22:30 p.m. for the Terra satellite. The MOD11_A2 product is Terra MODIS LST and Emissivity eight-day V.5 data (derived from the daily 1-km LST product). These data include day and night acquisitions and are stored on a 1-km sinusoidal grid as the average values of clear-sky LSTs during an eight-day period. The MODIS/Terra Land Surface Temperature/Emissivity products were validated over a widely-distributed set of locations and time periods via several ground-truth and validation efforts.

The Operational Land Imager (OLI) and Thermal Infrared Sensor (TIRS) are onboard Landsat 8, launched in February 2013. The OLI offers several enhancements from prior Landsat instruments, with the addition of two new spectral bands: a deep blue visible channel (Band 1) and a new infrared channel (Band 9). Two thermal infrared bands, i.e., TIRS, capture data with 100-m resolution. They are registered and delivered with 30-meter spatial resolution. The Landsat surface reflectance data product for Landsat 8 is generated from the Landsat 8 Surface Reflectance (L8SR) algorithm and was used to derive land cover and land surface characteristics in this study. The TIRS data were used to extract daytime LST.

3. Methodology

3.1. Computation of Daytime Land Surface Temperatures and Emissivity

LST was retrieved by applying the split-window algorithm from Landsat 8 TIRS data. TIRS data were converted to TOA spectral radiance using the radiance rescaling factors provided in the metadata file using Equation (1):

$$L_{\lambda }=ML\times Q_{CAL}+AL$$

(1)

where $L_{\lambda }$ is at-sensor spectral radiance (W/(m²∙sr∙μm)), M_L is the band-specific multiplicative rescaling factor, A_L is the band-specific additive rescaling factor and Q_CAL is the quantized and calibrated standard product pixel values (DN). Spectral radiance was then converted to brightness temperature using the thermal constants provided in the metadata file. The at-sensor brightness temperature assumes that the Earth’s surface is a black body (i.e., spectral emissivity is 1) and includes atmospheric effects (absorption and emissions along path) [36]. At-sensor spectral radiance was converted into at-sensor brightness temperature using Equation (2):

$$T=K2/\ln ((K1/L\lambda )+1)$$

(2)

where T is the effective at-sensor brightness temperature (K), K2 is the Calibration constant 2 in K, K1 is the Calibration Constant 1 (W/(m²∙sr∙μm)) and ${\mathrm{L}}_{\mathsf{\lambda }}$ is spectral radiance at the sensor’s aperture (W/(m²∙sr∙μm)). The split-window algorithm was developed by [37,38,39] (Equation (3)).

$$\begin{array}{l}{T}_S=T_i+c_1(T_i-T_j)+c_2{(T_i-T_j)}^2+c_0\\ +(c_3+c_{4}w)(1-\epsilon )(c_5+c_{6}w)\Delta \epsilon \end{array}$$

(3)

where T_i and T_j are at-sensor brightness temperatures at the TIRS bands i and j (in K), $\mathsf{\epsilon }$ is the mean emissivity, $\Delta \mathsf{\epsilon }$ is the emissivity difference, W is the total atmospheric water vapor content (in g·cm⁻²) and c₀ to c₆ are the coefficients to be determined from simulated data.

Land surface emissivity (LSE) was estimated from the OLI VNIR bands. The computation of LST was based on fractional vegetation cover (FVC) and was calculated using NDVI images, with NDVI-min from the dry soil and NDVI-max from dense vegetation (Equation (5)).

$$NDVI=\frac{{\rho }_{NIR}-{\rho }_{RED}}{{\rho }_{NIR}+{\rho }_{RED}}$$

(4)

$$FVC={\left[\frac{NDVI-NDV{\mathrm{I}}_{min}}{NDV{\mathrm{I}}_{max}-NDV{\mathrm{I}}_{min}}\right]}^2$$

(5)

where $\rho RED$ and $\rho NIR$ are the reflectance of red and NIR bands. ε is calculated using Equation (6) [35].

$$\begin{array}{cc}\epsilon ={\epsilon }_S(1-FVC)+{\epsilon }_{V}FVC\hfill & (0<FVC<1)\\ \epsilon =0.99\hfill & (FVC=1)\\ \epsilon =a+b{\rho }_{red}\hfill & (FVC=0)\end{array}$$

(6)

where a and b are correlation coefficients of the linear regression of the red band and emissivity. ${\mathsf{\epsilon }}_S$ and ${\mathsf{\epsilon }}_V$ are soil and vegetation emissivity (0.971 and 0.987 for TIRS1, 0.977 and 0.989 for TIRS2, respectively) obtained from the ASTER spectral library [40,41].

For a better comparison among images, LST values were scaled between the minimum and maximum values. These values were identified in each LST image and were used to calculate the normalized temperature values (Equation (7)):

$$NLST=\frac{\left(LST-LS{T}_{\min }\right)}{\left(LS{T}_{\max }-LS{T}_{\min }\right)}$$

(7)

where NLST is normalized land surface temperature, LST is land surface temperature for a given pixel, LST_min is the minimum and LST_max is the maximum LST value in an image.

3.2. SUHI Analysis

MODIS 8-day average LST at 1-km resolution of nighttime acquisitions was resampled to monthly values over the study period from September 2013 to September 2015. LST from landsat-8 TIRS was also averaged for each month with temporal synchronization to the MODIS LSTs. Three SUHI indicators were used to assess SUHI intensity in day and night and seasonal variations. The urban and rural area difference in the average temperature method proposed by [42] (Equation (8)) was adapted to identify SUHI variations. In addition, the urban-agricultural difference method [43] (Equation (9)) and the urban-water difference method [44] (Equation (10)) were also adapted for the purpose of comparisons.

$$SUH{I}_1=LS{T}_{urban}-LS{T}_{rural}$$

(8)

$$SUH{I}_2=LS{T}_{urban}-LS{T}_{agriculture}$$

(9)

$$SUH{I}_3=LS{T}_{urban}-LS{T}_{water}$$

(10)

where LST_urban, LST_rural, LST_agriculture and LST_water are the monthly average temperature for urban, rural, agriculture and water areas, respectively.

3.3. Derivation of Surface Biophysical Variables

Land cover types were categorized, using the maximum likelihood classifier, into built-up, vegetation, soil and water classes (Figure 2e). The monthly average temperature by land cover class was calculated. Furthermore, to investigate the relationship between LST and surface biophysical characteristics, we employed four surface biophysical and physical descriptors: impervious surface (IS), surface albedo, NDVI and elevation (Figure 2a–e). The ASTER-based digital elevation model (DEM) was used to derive the elevation data (Figure 2d). A negative correlation between NDVI or FVC and LST has been found in previous studies [27,45,46,47,48], while a positive relationship of IS with LST was noted in SUHI modeling [21,49]. To extract IS, we used normalized spectral mixture analysis (NSMA) [50] to reduce the diversity of urban brightness and the choice of the properties of the endmembers. In this method, the reflectance value was normalized as:

$${\overline{R}}_b=\frac{R_b}{\mu }\times 100\hspace{1em}\text{where}\hspace{1em}\mu =\frac{1}{N}{\displaystyle \sum _{b=1}^N{R}_b}$$

(11)

where ${\overline{R}}_b$ is the normalized reflectance of a pixel for band b; R_b is the reflectance for band b; $\mathsf{\mu }$ is the average reflectance for that pixel; and N is the total number of bands. With the normalized spectra, a fully-constrained linear spectral mixture analysis (SMA) model was applied to quantify urban composition:

$${\overline{R}}_b={\displaystyle \sum _{i=1}^N{\overline{f}}_i{R}_{i,b}+e_b}\hspace{1em}\text{where}\hspace{1em}{\displaystyle \sum _{i=1}^N{\overline{f}}_i=1 and {\overline{fi}}^{3}0}$$

(12)

where R_i,b is the normalized reflectance of endmember i in band b for that pixel; ${\overline{f}}_i$ is the fraction of endmember i; and e_b is residual. The impervious surfaces fraction obtained from the model is shown in Figure 2a.

The last biophysical feature was albedo. The effect of albedo on the SUHI has been studied by [5,14]. These studies concluded that the use of high-albedo materials decreased solar radiation absorption and reduced LST. Several algorithms were proposed by [51] to derive broadband albedo by using different band combinations. By matching the corresponding bands, we used the TM/ETM+ algorithm to retrieve albedo with the OLI bands by Equation (13):

$$\begin{array}{l}{\alpha }_{short}=0.365{\alpha }_2+0.130{\alpha }_4+0.373{\alpha }_5+0.085{\alpha }_6\\ +0.072{\alpha }_7-0.0018\end{array}$$

(13)

where ${\alpha }_{short}$ is total short wave albedo, ${\alpha }_2,{\alpha }_4,{\alpha }_5,{\alpha }_6,{\alpha }_7$ are the spectral reflectance of OLI Band 2, Band 4, Band 5, Band 6 and Band 7, respectively.

4. Results and Discussion

4.1. LST Analysis

Figure 3 shows the box plot of day and night LST data. In daytime LST, the peak temperature was observed in August, while in nighttime LST, the peak temperature was observed in July. Minimum temperatures for both day and night were observed in February. NLST showed the distribution of temperature data between high temperature and low temperature and can be used to compare the spatial and temporal distribution of SUHI in different months. According to the boxplot of NLST (Figure 3c,d), the nighttime NLST showed overall higher values than the daytime NLST. A large area of built-up cover corresponded to a low and high value of NLST in day and night, respectively.

The spatial distributions of NLST in day and night are shown in Figure 4 and Figure 5, respectively. Figure 4 shows that except for the western part of the city where many industries and an airport were located, the rest of the urban areas were cooler than the surrounding area in different seasons. In the nighttime, the downtown areas became hottest, and the surrounding rural area was found colder, with some changes in the spatial pattern in different seasons (Figure 5).

4.2. SUHI Analysis

For each land cover class, mean LST was computed at day and night of different months. Figure 6 shows temporal plots of average LST by land cover. The highest and lowest temperatures in daytime were observed in bare soil and water, respectively. At nighttime, built-up and bare soil classes exhibited the highest and lowest temperatures, respectively. Moreover, at daytime, the temperature variations by land cover were high among different months and seasons of year. The temperature difference among the land cover classes was very high in spring and summer, but low in winter and autumn (Figure 6a). However, at nighttime, the temperature difference among the land cover classes was lower and more stable (Figure 6b).

Figure 7 shows calculated SUHI intensity values. With the urban-rural LST difference method (Figure 7a), the surface cool island was observed, with the maximum value in mid-March, early spring, in Tehran. Night SUHI intensity from the urban-rural difference method yielded positive values with maximum values observed in spring, which correspond to the maximum amount of NDVI. Results of the urban-agriculture difference method (Figure 7b) discovered high SUHI values in day with extreme seasonal variations (maximum values in spring and summer and minimum values in winter and autumn) and low SUHI values at nighttime with insignificant seasonal variations. This phenomenon was caused by the temperature differences between green vegetation and built-up classes in day and night (Figure 6). The third SUHI approach investigated in this paper was the urban-water LST difference. The result of this approach revealed the high SUHI intensity in day and very low SUHI at night (Figure 7c). This phenomenon was caused by a huge temperature difference between water and built-up areas in day and little temperature differences at nighttime (Figure 6).

Table 1. Monthly SUHI intensity values of daytime with different calculation methods (urban-rural (U-R), urban-agriculture (U-A) and urban-water (U-W) approaches). Fields marked with orange color indicate the maximum value of SUHI and those in blue the minimum value of SUHI during the year.

SUHI Method	Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec
U-R Difference	−3.5	$-0.9$	$-4$	−2	−1.8	−2.3	−2.4	−2.6	−2.7	−2.4	$-0.9$	−3.3
U-A Difference	$0.5$	3.2	1.4	5	$8.2$	6.9	8	6.9	7	6	3.3	0.8
U-W Difference	4.8	1.2	11.3	13.8	14.3	15.5	13.4	$14.4$	11.5	9	$0.91$	2.1

and

Table 2. Monthly SUHI intensity values of nighttime with different calculation methods. Fields marked with orange color indicate the maximum value of SUHI and those in blue the minimum value of SUHI during the year.

SUHI Approach	Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec
U-R Difference	2.8	$2.3$	3.4	3.8	$3.9$	3.7	2.9	3.2	3.2	3.2	3.4	2.8
U-A Difference	$1.1$	1.2	1.5	2.3	2.5	2.1	2.3	2.5	$2.9$	1.8	2	1.8
U-W Difference	0.49	0.65	−0.04	−0.1	−0.01	−0.1	$-0.5$	$-0.5$	−0.4	0.46	$0.61$	0.22

show monthly SUHI intensity values of daytime and nighttime with different calculation methods. The maximum monthly SUHI intensity values with all three methods in day and night were 15.5 K and 3.9 K, respectively, and minimum monthly SUHI intensity values were −4 K and −0.5 K, respectively.

4.3. Relationship between LST and Surface Properties

Monthly NDVI and albedo were averaged over the study period. The box plot of monthly NDVI (Figure 8a) shows that the max-NDVI value was in May, because the greatest amount of green vegetation was found in May in this semi-arid area. Shortwave albedo displayed a monthly change (Figure 8b), with the greatest value found in summer time and a reduction of the value in winter. The city had both deciduous and evergreens trees, which caused an irregular seasonal spatial distribution of green vegetation cover as indicated by FVC (Figure 9). Agricultural land in southern Tehran, which was used for growing vegetables, did not follow regular spatial-temporal patterns of cultivation, but followed the market needs. The different cultivation in agricultural land and different phenology of plants in the urban green space area caused the seasonal variations of FVC spatial distribution, so that in the winter FVC image, deciduous trees were distinguishable from evergreen trees in the urban area. These changes in FVC influenced the spatial distribution of LST in different seasons.

To find out the correlation between LST and surface biophysical properties, seasonal normalized LST, averaged from monthly NLST in day and night over the study period, was computed. A total of 500 randomly-selected samples were chosen to investigate the relationship between LST and FVC, IS, albedo and elevation in different seasons. Pearson correlation was conducted to examine the strength of bivariate associations between LST and the surface variables. The results of correlation analysis are summarized in

Table 3. Pearson correlation coefficients between NLST (day and night) and FVC, albedo, impervious surface (IS) and elevation in different seasons of the year. Fields marked with orange and blue colors indicate maximum and minimum correlations between NLST and each of the variables in different seasons of the year.

	Winter		Spring		Summer		Autumn
	NLST-	NLST-	NLST-	NLST-	NLST-	NLST-	NLST-	NLST-
	Day	Night	Day	Night	Day	Night	Day	Night
FVC	0.313	0.070	−0.367	−0.048	$-0.410$	−0.087	0.220	$-0.002$
Albedo	0.099	$-0.527$	0.051	$-0.050$	0.274	−0.246	0.233	−0.372
IS	−0.233	0.466	$-0.171$	$0.601$	−0.245	0.596	−0.227	0.600
Elevation	−0.295	−0.720	$0.006$	$-0.764$	0.134	−0.651	−0.248	−0.705

. It is shown that the correlation changed significantly with seasons. The maximum of the correlation coefficient was observed in the relationship between nighttime NLST and elevation in spring (−0.76), nighttime NLST and IS in spring (0.60), nighttime NLST and albedo in winter (−0.53) and daytime NLST with FVC in summer (−0.41), respectively. The minimum of the correlation coefficient was observed in the relationship between nighttime NLST and FVC in autumn (−0.002), daytime NLST and elevation in spring (0.006), nighttime NLST and albedo in spring (−0.05) and daytime NLST with IS in spring (−0.17), respectively. Our results showed a positive relationship between daytime LST and FVC in autumn and winter. The reason for this unexpected result might be related to the freezing of other land covers than vegetation cover in these seasons, because water content in vegetation retained heat against the cold and freezing. The low leaf area of deciduous trees and annual plants in these seasons and the reduction of photosynthesis can also be the reasons for the positive correlation. Pearson correlation between LST and albedo was positive in day and negative at night, which might be caused by the high brightness of bare soils with high albedo and LST at day and low LST at night. Impervious surfaces detected a strong positive correlation with LST at night. Impervious surfaces absorbed shortwave solar energy during daytime and released it into the atmosphere at night. This causes impervious surfaces to display a higher temperature than the other surfaces at the time of the Terra satellite passing (22.30 p.m.). During the day, IS discovered a negative relationship with LST due to the presence of shadows cast by high-rise buildings [52], which contributed to the SUHI sink in the semi-arid areas. There was a high negative correlation between temperature and elevation at night. In the daytime, the highlands north and east of Tehran were affected by direct sunlight and quickly warmed compared to the lowlands. However, at nighttime, highlands with no vegetation cover lost their heat rapidly. In addition, high-rise buildings prevented the blowing of the mountain breeze into the valley, retaining hot air in the downtown areas. Figure 10 shows the matrix plot of surface variable data and day and night land surface temperature in different seasons.

5. Conclusions

In this study, we analyzed the seasonal SUHI variations in Tehran, Iran, by using LSTs derived from Terra MODIS and Landsat 8 from 2013 to 2015. The observed inversed SUHI, the surface urban cool island, in daytime was found, because the surrounding rural areas were mostly barren soils with a higher temperature than the urban areas. However, at nighttime, the downtown detected a higher temperature. The existence of SUHI at nighttime stemmed from three reasons: (1) rural areas at night, due to low thermal capacity and emissivity, lost their heat faster than the downtown; (2) vehicular traffic continued until midnight in downtown; and (3) high-rise buildings prevented the blowing of the mountain breeze into the valley, resulting in hot air remaining in the downtown areas. The urban-agriculture and urban-water difference methods revealed the high SUHI values at daytime with extreme seasonal variations (maximum values in spring and summer and minimum in winter and autumn) and low SUHI values at nighttime with insignificant seasonal variations. The relationship between LST and the surface biophysical variables displayed a substantially seasonal variation. A positive relationship was observed between daytime LST and FVC in the autumn and winter, which may be attributed to the freezing of other land covers compared to vegetation cover in these seasons, because the water content in vegetation retained heat against the cold and freezing. The low leaf area of deciduous trees and annual plants in this season and the reduction of photosynthesis can explain largely the positive correlation between daytime LST and FVC. Maximal correlation was observed in the relationship between nighttime LST and elevation in spring, nighttime LST and IS in spring, nighttime LST and albedo in winter and daytime LST with FVC in summer. The relationship between all surface biophysical variables with daytime LST discovered large seasonal variations, which implies that it may not be appropriate to use these relationships for SUHI modeling, except for elevation and IS, which modulated night SUHI to a large extent.

In this study, SUHI was examined in a semi-arid city. In such a city, the SUHI phenomenon often did not exist [53]. Higher temperature in barren lands/soils around the city contributed to the generation of a surface urban cool island. Barren soils had low heat capacity and conductivity and were heated by sunrise quickly, while urban surfaces were saving solar energy, and daytime images were not acquired at the peak of solar radiation. Therefore, satellite analysis of SUHIs in semi-arid cities requires at least two images, one at daytime and one at nighttime.

UHI studies with remotely-sensed data are cost effective and less time consuming than in situ data, since remote sensing data creates a synoptic view of the spatial distribution of LST [17]. However, some challenging issues exist with UHI studies by remote sensing data. The retrieval of LSE in urban areas is still unresolved because of the variation of LSE with building materials, urban features and geometry, although various methods have been developed to retrieve LSE in urban areas, for example sub-pixel estimation [54], the classification-based method [55], the urban emissivity library [56] and estimating effective emissivity using the sky view factor [57]. These methods were able to solve the mentioned problem partially. However, emissivity varies with the type of impervious surface, which was not considered in the sub-pixel estimation method. The classification-based estimation is subject to the spatial resolution and acquisition date of image data and the classification result. Using thermal inertia data may improve retrieval of LSE in the urban areas. Apparent thermal inertia (ATI) can be retrieved by day and night thermal images. ATI shows the spatial distribution of diurnal variation of LST, which is associated with LSE. Another issue is different definitions and methods of measuring the intensity of SUHI. The most common method of measuring the intensity is the urban and rural area difference in average temperature method [42]. The variation of SUHI intensity and SUHI indicators has been discussed in [30,58]. The intensity of SUHI may change due to the size of the study area and SUHI indicators. In addition, this study compared LSTs only between the urban and the rural surfaces and did not assess the vertical distribution of UHI in the urban canopy layer and UBL. The spatial variation of LST can be more significant within the urban area as compared to the rural area owing to the complexity of land use and land cover in the urban area environment [59]. It would be interesting to assess the LST variation in the urban area with different eco-climatic settings. It may also be possible for future studies to use the thermal and radiation properties of urban surfaces and 3D data to analyze the vertical dimension of UHI.