Continent-Wide 2-D Co-Seismic Deformation of the 2015 Mw 8.3 Illapel, Chile Earthquake Derived from Sentinel-1A Data: Correction of Azimuth Co-Registration Error
Abstract
:1. Introduction
2. ISD Method for Co-Registering Multiple S1A TOPS Frames
2.1. ISD Method
2.2. Procedure of S1A TOPS SLC Co-Registration with ISD
- Step 1: initial co-registration. Estimate initial SLC images offset and set up SLC resampling look-up table [24] with orbital state vectors and an external DEM, e.g., SRTM DEM, and resample the slave SLC into master imaging geometry.
- Step 2: co-registration by the CC method. Determine the image offsets between master and the resampled slave SLC from Step 1 by the CC method, and use the image offsets to refine the look-up table. The original slave SLC is, again, resampled into master imaging geometry.
- Step 3: co-registration by ISD method. Calculate the mean phase differences of all bursts overlaps between the master and the resampled slave SLC from Step 2. Then the constant azimuth offset and the change rate are resolved by ISD method. The look-up table is refined with an azimuth offset calculated from Equation (2) and the estimated parameters and, finally, output the resampled slave SLC using the ultimately-refined look-up table.
3. Data Processing
3.1. Co-Registering Multiple Frames of S1A TOPS Data
3.2. D-InSAR and Offset Tracking Processing
3.3. Precision Assessment and 2-D Displacement Retrieval
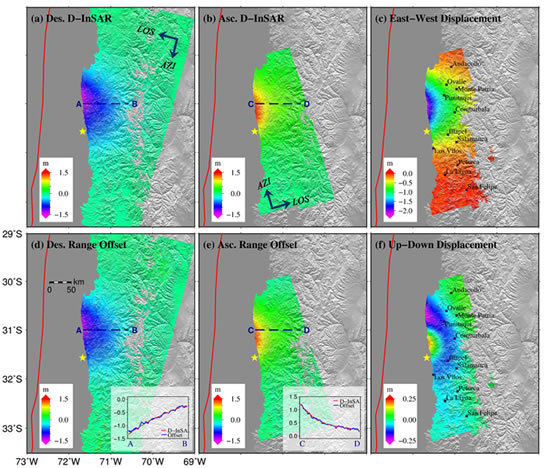
4. Results
5. Discussion
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Usgs Earthquake Hazards Program, m8.3-48km w of Illapel, Chile, 2015. Available online: http://earthquake.Usgs.Gov/earthquakes/eventpage/us20003k7a#general_summary (accessed on 30 October 2015).
- Pacific tsunami Warning Center (PTWC). Widespread Hazardous Tsunami Waves Are Possible along the Coast of Chile and Peru, 2015. Available online: http://ptwc.Weather.Gov/ptwc/text.Php?Id=pacific.Tsupac.2015.09.16.2301 (accessed on 30 October 2015).
- Moreno, M.; Rosenau, M.; Oncken, O. 2010 maule earthquake slip correlates with pre-seismic locking of andean subduction zone. Nature 2010, 467, 198–202. [Google Scholar] [CrossRef] [PubMed]
- Usgs Earthquake Hazards Program, m8.3 Coastal Chile Earthquake of 16 September 2015. Available online: http://earthquake.Usgs.Gov/earthquakes/eqarchives/poster/2015/20150916.Php (accessed on 30 October 2015).
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M. Gmes sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Schubert, A.; Small, D.; Miranda, N.; Geudtner, D.; Meier, E. Sentinel-1a product geolocation accuracy: Commissioning phase results. Remote Sens. 2015, 7, 9431–9449. [Google Scholar] [CrossRef]
- De Zan, F.; Guarnieri, A.M. Topsar: Terrain observation by progressive scans. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2352–2360. [Google Scholar] [CrossRef]
- Grandin, R.; Vallée, M.; Satriano, C.; Lacassin, R.; Klinger, Y.; Simoes, M.; Bollinger, L. Rupture process of the Mw = 7.9 2015 gorkha earthquake (Nepal): Insights into himalayan megathrust segmentation. Geophys. Res. Lett. 2015, 42, 8373–8382. [Google Scholar] [CrossRef]
- González, P.J.; Bagnardi, M.; Hooper, A.J.; Larsen, Y.; Marinkovic, P.; Samsonov, S.V.; Wright, T.J. The 2014–2015 eruption of fogo volcano: Geodetic modeling of Sentinel-1 TOPS interferometry. Geophys. Res. Lett. 2015, 42, 9239–9246. [Google Scholar] [CrossRef]
- Salvi, S.; Stramondo, S.; Funning, G.; Ferretti, A.; Sarti, F.; Mouratidis, A. The Sentinel-1 mission for the improvement of the scientific understanding and the operational monitoring of the seismic cycle. Remote Sens. Environ. 2012, 120, 164–174. [Google Scholar] [CrossRef]
- Wen, Y.; Xu, C.; Liu, Y.; Jiang, G. Deformation and source parameters of the 2015 Mw 6.5 earthquake in pishan, western China, from Sentinel-1a and ALOS-2 data. Remote Sens. 2016, 8, 134. [Google Scholar] [CrossRef]
- Kim, J.-W.; Lu, Z.; Degrandpre, K. Ongoing deformation of sinkholes in wink, texas, observed by time-series Sentinel-1a SAR interferometry (preliminary results). Remote Sens. 2016, 8, 313. [Google Scholar] [CrossRef]
- Esa, Scientific Data Hub. Avaliable online: https://scihub.Copernicus.Eu/ (accessed on 30 December 2015).
- Prats-Iraola, P.; Scheiber, R.; Marotti, L.; Wollstadt, S.; Reigber, A. TOPS interferometry with TerraSAR-x. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3179–3188. [Google Scholar] [CrossRef]
- De Zan, F.; Prats-Iraola, P.; Scheiber, R.; Rucci, A. Interferometry with TOPS: Coregistration and azimuth shifts. In Proceedings of 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 3–5 June 2014; pp. 1–4.
- Wegmüller, U.; Werner, C.; Strozzi, T.; Wiesmann, A.; Frey, O.; Santoro, M. Sentinel-1 support in the gamma software. In Proceedings of the Fringe 2015 Conference, ESA ESRIN, Frascati, Italy, 23–27 March 2015; pp. 23–27.
- Sandwell, D.; Mellors, R.; Tong, X.; Wei, M.; Wessel, P. Open radar interferometry software for mapping surface deformation. EOS Trans. Am. Geophys. Union 2011, 92, 234. [Google Scholar] [CrossRef]
- Scheiber, R.; Moreira, A. Coregistration of interferometric SAR images using spectral diversity. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2179–2191. [Google Scholar] [CrossRef]
- Scheiber, R.; Jager, M.; Prats-Iraola, P.; De Zan, F.; Geudtner, D. Speckle tracking and interferometric processing of TerraSAR-x TOPS data for mapping nonstationary scenarios. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1709–1720. [Google Scholar] [CrossRef]
- Grandin, R. Interferometric processing of SLC Sentinel-1 TOPS data. In Proceedings of the 2015 ESA Fringe Workshop, Frascati, Italy, 23–27 March 2015.
- Hooper, P.M. Iterative weighted least squares estimation in heteroscedastic linear models. J. Am. Stat. Assoc. 1993, 88, 179–184. [Google Scholar]
- Hu, J.; Wang, Q.; Li, Z.; Zhao, R.; Sun, Q. Investigating the ground deformation and source model of the yangbajing geothermal field in Tibet, China with the WLS InSAR technique. Remote Sens. 2016, 8, 191. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, R.; Hu, J.; Wen, L.; Feng, G.; Zhang, Z.; Wang, Q. InSAR analysis of surface deformation over permafrost to estimate active layer thickness based on one-dimensional heat transfer model of soils. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Sansosti, E.; Berardino, P.; Manunta, M.; Serafino, F.; Fornaro, G. Geometrical SAR image registration. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2861. [Google Scholar] [CrossRef]
- Jung, H.-S.; Lee, W.-J.; Zhang, L. Theoretical accuracy of along-track displacement measurements from multiple-aperture interferometry (MAI). Sensors 2014, 14, 17703–17724. [Google Scholar] [CrossRef] [PubMed]
- Feng, G.; Xu, B.; Shan, X.; Li, Z.; Zhang, G. Coseismic deformation and source parameters of the 24 September 2013 awaran, pakistan m (w) 7. 7 earthquake derived from optical Landsat 8 satellite images. Chin. J. Geophys. 2015, 58, 1634–1644. [Google Scholar]
- Feng, G.; Li, Z.; Shan, X.; Xu, B.; Du, Y. Source parameters of the 2014 Mw 6.1 south Napa earthquake estimated from the Sentinel 1a, cosmo-skymed and GPS data. Tectonophysics 2015, 655, 139–146. [Google Scholar]
- Li, Z.; Ding, X.; Huang, C.; Zhu, J.; Chen, Y. Improved filtering parameter determination for the goldstein radar interferogram filter. ISPRS J. Photogramm. Remote Sens. 2008, 63, 621–634. [Google Scholar] [CrossRef]
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Ko, S.J.; Lee, Y.H. Center weighted median filters and their applications to image enhancement. IEEE Trans. Circuits Syst. 1991, 38, 984–993. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Jo, M.-J.; Jung, H.-S.; Won, J.-S. Detecting the source location of recent summit inflation via three-dimensional InSAR observation of Kīlauea volcano. Remote Sens. 2015, 7, 14386–14402. [Google Scholar] [CrossRef]
- Li, Z.; Yang, Z.; Zhu, J.; Hu, J.; Wang, Y.; Li, P.; Chen, G. Retrieving three-dimensional displacement fields of mining areas from a single InSAR pair. J. Geod. 2015, 89, 17–32. [Google Scholar] [CrossRef]
- Samsonov, S.; Tiampo, K.F.; Rundle, J.B. Application of DinSAR-GPS optimization for derivation of three-dimensional surface motion of the southern California region along the san andreas fault. Comput. Geosci. 2008, 34, 503–514. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.; Ding, X.; Zhu, J.; Zhang, L.; Sun, Q. Resolving three-dimensional surface displacements from InSAR measurements: A review. Earth Sci. Rev. 2014, 133, 1–17. [Google Scholar] [CrossRef]
- Zhan, W.J.; Li, Z.W.; Wei, J.C.; Zhu, J.J.; Wang, C.C. A strategy for modeling and estimating atmospheric phase of SAR. Chin. J. Geophys. 2015, 58, 2320–2329. [Google Scholar]
- Insarapp Project, Chile Earthquake: Sentinel-1 InSAR Analysis. Available online: http://insarap.Org/ (accessed on 30 October 2015).
- Grandin, R.; Klein, E.; Métois, M.; Vigny, C. Three-dimensional displacement field of the 2015 Mw 8.3 illapel earthquake (Chile) from across- and along-track Sentinel-1 TOPS interferometry. Geophys. Res. Lett. 2016, 43. [Google Scholar] [CrossRef]
- Delouis, B.; Nocquet, J.M.; Vallée, M. Slip distribution of the 27 February 2010 Mw = 8.8 maule earthquake, central Chile, from static and high-rate GPS, InSAR, and broadband teleseismic data. Geophys. Res. Lett. 2010, 37, 1–7. [Google Scholar] [CrossRef]
- Elliott, J.; Elliott, A.; Hooper, A.; Larsen, Y.; Marinkovic, P.; Wright, T. Earthquake monitoring gets boost from a new satellite. Eos 2015, 96, 14–18. [Google Scholar] [CrossRef]
- Geudtner, D.; Torres, R.; Snoeij, P.; Ostergaard, A.; Navas-Traver, I. Sentinel-1 mission capabilities and SAR system calibration. In Proceedings of the 2013 IEEE Radar Conference (RadarCon), Ottawa, ON, Canada, 29 April–3 May 2013; pp. 1–4.
- Jiang, M.; Li, Z.; Ding, X.; Zhu, J.-J.; Feng, G. Modeling minimum and maximum detectable deformation gradients of interferometric SAR measurements. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 766–777. [Google Scholar] [CrossRef]
- Xu, W.; Burgmann, R.; Li, Z. An improved geodetic source model for the 1999 Mw 6.3 Chamoli earthquake, India. Geophys. J. Int. 2016, 205, 236–242. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, L.; Hu, J.; Ding, X.; Li, Z.; Zhu, J. Characterizing sudden geo-hazards in mountainous areas by DinSAR with an enhancement of topographic error correction. Nat. Hazard. 2015, 75, 2343–2356. [Google Scholar] [CrossRef]




| Acquisition Date | Orbit Direction | Track | No. of Frame | No. of Total Burst | B⊥ (m) |
|---|---|---|---|---|---|
| 24 August 2015 | Ascending | 18 | 2 | 36 1 = 2 × 2 × 9 | 70 |
| 17 September 2015 | Ascending | 18 | 2 | 36 = 2 × 2 × 9 | |
| 26 August 2015 | Descending | 156 | 3 | 84 = 3 × 2 × 9 | −116 |
| 19 September 2015 | Descending | 156 | 3 | 84 = 3 × 2 × 9 |
| Interferometric Pair | CC Method | ISD Method | ||
|---|---|---|---|---|
| Azimuth (Pixel) | Range (Pixel) | Azimuth (Pixel) | Range (Pixel) | |
| 24 August 2015–17 September 2015 | 0.1170 | 0.0516 | 0.00104 | --- |
| 26 August 2015–19 September 2015 | 0.0827 | 0.0425 | 0.00095 | --- |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, B.; Li, Z.; Feng, G.; Zhang, Z.; Wang, Q.; Hu, J.; Chen, X. Continent-Wide 2-D Co-Seismic Deformation of the 2015 Mw 8.3 Illapel, Chile Earthquake Derived from Sentinel-1A Data: Correction of Azimuth Co-Registration Error. Remote Sens. 2016, 8, 376. https://doi.org/10.3390/rs8050376
Xu B, Li Z, Feng G, Zhang Z, Wang Q, Hu J, Chen X. Continent-Wide 2-D Co-Seismic Deformation of the 2015 Mw 8.3 Illapel, Chile Earthquake Derived from Sentinel-1A Data: Correction of Azimuth Co-Registration Error. Remote Sensing. 2016; 8(5):376. https://doi.org/10.3390/rs8050376
Chicago/Turabian StyleXu, Bing, Zhiwei Li, Guangcai Feng, Zeyu Zhang, Qijie Wang, Jun Hu, and Xingguo Chen. 2016. "Continent-Wide 2-D Co-Seismic Deformation of the 2015 Mw 8.3 Illapel, Chile Earthquake Derived from Sentinel-1A Data: Correction of Azimuth Co-Registration Error" Remote Sensing 8, no. 5: 376. https://doi.org/10.3390/rs8050376
APA StyleXu, B., Li, Z., Feng, G., Zhang, Z., Wang, Q., Hu, J., & Chen, X. (2016). Continent-Wide 2-D Co-Seismic Deformation of the 2015 Mw 8.3 Illapel, Chile Earthquake Derived from Sentinel-1A Data: Correction of Azimuth Co-Registration Error. Remote Sensing, 8(5), 376. https://doi.org/10.3390/rs8050376