1. Introduction
It is well-established the importance of accurately accounting for surface roughness conditions over agricultural lands as a requirement for retrieving near-surface soil moisture from microwave remotely-sensed Synthetic Aperture Radar (SAR) images. Despite the fact that there are a number of intrinsic roughness-related applications, such as in agricultural studies (e.g., monitoring tillage activities, crop residue cover,
etc.) [
1] and in geological surveys (e.g., characterization and classification of lava flows, alluvial deposits, desert surfaces,
etc.) [
2], roughness is mostly understood as a disturbing factor in what respects to soil moisture estimation from SAR imagery. The reason is that the dynamic range of the backscatter response due to surface roughness is comparable to that of near-surface soil moisture. From a model standpoint, this soil roughness can be considered as the stochastic varying height of the soil surface towards a reference surface [
3] (Volume II). This reference surface can be the unperturbed surface of a periodic pattern or can be the mean surface if only random variations exist.
In dealing with microwave remote sensing a range of surface roughness components are involved in the scattering response of agricultural lands. In fact, roughness can be considered as the sum of different soil components corresponding to different scales [
4]:
- (a)
a small scale (millimeter to centimeter scale) involving grains, individual soil aggregates and soil clods, which represent a non-oriented, random component;
- (b)
a medium scale (centimeter to decimeter scale) related to furrows or tillage rows, which represent an oriented, periodic, deterministic component; and
- (c)
a large scale (decimeter to meter, pixel-sized scale) related to local topographic trends such as field slope, which defines the aspect of the land surface relative to the observation geometry of the sensor.
In terms of the sensor wavelength
λ and for soil moisture applications (
i.e., in the microwave portion of the spectrum), the random component involves dimensions of roughly
and contributes mostly with the incoherent component of the total scattered energy, whereas the periodic pattern of the medium scale, with dimensions of about
λ, mainly accounts for the coherent component. The large scale (~10
λ) determines the local incidence angle which in turn affect both the coherent and the incoherent components [
3,
5] (Chapter 12). In opposite to the large-scale (natural) component, both small- and medium-scale (man-made) components arise from tillage operations over the soil and are affected by weathering and erosion processes such as rainfall, runoff and wind.
The statistical properties of the soil roughness random component may be summarized using only two parameters derived from one-dimensional (1-D) profiles: the surface height standard deviation (s) and the surface correlation length (l), once the shape of the autocorrelation function (ACF) has been fixed. The height standard deviation describes the random variation in surface elevation with respect to a predefined reference surface, this being the mean plane when neither furrow structure nor tillage pattern are present. The autocorrelation function measures the degree of spatial dependence between points, whereas the correlation length indicates at what extent two separate points can be considered correlated. A complementary way to characterize 1-D rough profiles is through its power spectral density, which states the relative strength of the spatial frequencies present in the profile.
There are a number of limiting factors in the accuracy of surface roughness parameters as derived from profiling techniques, such as the profile length or measurement extent and the sampling interval or sampling distance, the later being the spacing between two contiguous height measurements. As for the profile length, for instance, experimental and numerical studies [
6,
7,
8] suggested the need for long profiles (
or ~25
) whereas other studies, focused on soil moisture retrieval rather than on soil roughness measurements [
9,
10,
11,
12,
13,
14], employed 1-m-long profiles, where no clear relationship between the reliability of the retrieved estimates and the profile length could be found. As for the sampling interval
, a rule of thumb recommended in [
3] (Volume II) stated that
provided that the corresponding change in height
z is
. This rule along with the Fraunhoffer criterion (which states that for smooth surfaces
) [
3,
15] leads to an upper bound
cm for a smooth surface (
) imaged by an L-band (
) sensor at
. On the other hand, numerical experiments with synthesized rough surfaces were used to assess the impact of the sampling interval on the accuracy of roughness parameters. According to [
16], the sampling interval should not exceed 0.1 times the actual (or true) correlation length (
l) for accurate parameterization of roughness. Larger sampling interval instruments cause that the roughness profile is sampled at an insufficient rate and therefore, very small structures are not presented in the obtained roughness profile. This subsampling mainly causes a change in slope of the ACF around zero [
16]. In this sense, in [
6] it is stated that the sampling interval should be smaller than
for the roughness parameters to be estimated within 5% error. It is worth mentioning the lack of experimental studies in this respect, with the exception of [
17] where such a study was performed over an experimental bare soil patch.
Typical
in-situ roughness measurement methods at field scale involve the use of contact profilers such as pinmeters or meshboards [
18]. More advanced profiling methods use non-contact, laser techniques such as triangulation [
19,
20] or time-of-flight distance meters [
7]. In the triangulation laser techniques, each laser-illuminated soil feature is recorded onto a picture by a camera and then transformed to a reference frame using a dedicated calibration procedure. The calibration procedure sets a polynomial transformation from pixel coordinates to millimeter coordinates in the reference frame. By means of a moving platform, contiguous pictures of adjacent soil features are recorded. Therefore, the sampling interval of the soil profiles is given by the sampling distance of the laser survey over the surface, providing non-overlapping measurements are performed. In the same way, the sampling interval in time-of-flight techniques is simply defined by the distance between two contiguous measurements the distance meter is positioned at. Using these techniques, measured profiles have generally a length between 1 m and 4 m, and a sampling interval between 1 mm and 20 mm [
18].
A valuable advantage of these laser techniques is that they are self-contained, yielding a high portability to their corresponding instruments that enables collecting multisite measurements over relative large extents. This is important, since recently-developed methods involving close range techniques, such as stereo-photogrammetric systems (see for instance [
21]), Structure from Motion [
22] or Terrestrial Laser Scanning [
17] are more suitable for multitemporal studies rather than for multisite surveys due to the need for setting up of reference targets on ground, for each site measurement. Moreover, in this sort of techniques the sampling interval depends on the particular experimental set-up chosen, mainly the distance between the camera and the soil patch. From the variety of roughness measurement techniques mentioned, it turns out the importance of quantifying the effect of different sampling intervals on roughness parameters in comparison to the smallest-sampling-interval measurements available, for instance, made at 1-mm.
The purpose of this paper is two-fold. First, an experimental study over a large soil roughness database is carried out to characterize and quantify the effect of the sampling interval on the 1-D roughness parameters
s and
l measured over agricultural lands under different tillages. This database is built from a long-term (2009–2011) field campaign in Argentinean Pampas Plain using a dedicated, custom-made, 2-D laser profiler named URSuLa. This first objective is now made possible by the small-sampling-interval capabilities of URSuLa, which enables it to synthesize profiles at different sampling intervals (
i.e., 2, 5, 10, 20 and 50 mm) by applying moving average techniques to the nominal, 1-mm-sampling-interval profiles. In the laser profiling technique used by URSuLa the sampling interval is given by the distance between two contiguous, non-overlapping samples of the laser line. This is a distinctive aspect of such a technique in comparison to more sophisticated techniques, such as the close range techniques above mentioned. Moreover, while accuracy of triangulation techniques are similar to the typical accuracies of close range techniques, the direct relation between sampling interval and the distance between two measurements enables the proposed study. Due to its extended measurement region (0.80 m × 0.25 m), URSuLa also enables the average of roughness descriptors computed from successive, contiguous profiles in order to diminish the statistical error. However, it is able to record only the small-scale roughness component, while the rest of the topography is not possible to characterize. The second goal is to present a simulation study to understand how the sampling-interval-dependent roughness parameters
s and
l impact on surface backscattering response, using the Integral Equation Model IEM2M [
23,
24] as scattering model. As a result, progress was made in the understanding of the different scales in soil surface roughness characterization and their impact on the microwave backscatter response of soil surfaces.
2. Experimental Details
2.1. Laser Profiler
The laser unit for surface surveys (
URSuLa) is a laser profiler which enables the measurement of soil roughness through 2-D digital modeling of the soil surface in an non-contact way.
Figure 1 depicts an scheme of the laser profiler. It comprises a rectangular parallelepiped-shaped metal frame with two guides, over which a mobile, motor-driven platform is mounted. Attached to the platform there are a laser unit, a case containing an optical system and a small, commercial-grade camera (Logitech
® QuickCam pro for Notebooks), at fixed locations. The platform is placed at a distance of 30 cm over the frame base. The laser beam points downwards and is scattered by a cylindrical lens within the case to obtain a laser line of 25 cm length over the ground surface with a beam width of 1 mm. The camera points obliquely to the laser line in such a way that its field of view includes the whole line. Pictures are taken by the camera (2 MP resolution), which is placed 20 cm off the laser beam and 20 cm over the ground. The focal length of the camera is 3.7 mm and the ground sampling distance is 0.25 mm/pixel. Under this set-up, the laser line depicts a transect of the surface mimicking its shape, and it is stored as digital information through the camera.
Calibration is done following the method described in [
19] to map pixel coordinates on the picture into millimeter coordinates over the ground. A transmission system coupled to the motor provides with longitudinal motion to the platform (see
Figure 1), so as to obtain a 0.80 m by 0.25 m scannable area. Opaque panels (not shown) are attached around the metal frame to avoid the solar daylight diminishing the contrast of the laser beam onto the soil surface. The laser profiler is capable of measuring surface heights with an accuracy of 1 mm. In planimetry, the accuracy is 0.5 mm in the direction of the laser line and 1 mm in the direction along the frame. In the direction along the laser line, the accuracy is given by the distance between two contiguous pixels onto the laser line transformed into the millimeter-reference frame using the polynomial transformation from the calibration step. Along the frame, the accuracy of the measurements is given by the accuracy in controlling the motor-driven platform which carries the laser. The platform motion is finely controlled by a stepper motor, which is positioned with an accuracy of 1 mm.
Figure 2 shows a digitalization from a ploughed surface with a clear furrow.
As for the portability, URSuLa weighs approximately 15 kg and is easily handled by a two-man team. Approximately half of its weight is due to a long-lasting battery (17 ampere-hour) which can be replaced by a lighter one provided a replacement back-up battery is available in the field. The battery feds the electronics as well as an embedded PC used to operate the device and to store the data. Once the device is positioned onto the ground surface, one full scan takes ~1 min. Most of the time spent in the field is dedicated to move from one point to the next carrying the device.
The sequence of processing the digital record involves two major steps. Firstly, the soil transect is identified in every picture based on the high contrast of the laser line relative to the soil surface. The pixel coordinates of the laser line onto the picture are transformed into millimeter coordinates and then stored in a matrix as heights and positions. This step is repeated after the platform is placed 1 mm away from the preceding position and until the entire surface extent is profiled. Secondly, the surface is assembled by joining all the transects using their position information relative to the metal frame stored in every picture. A 3-D render of the surface is generated at a 1 mm by 1 mm sampling interval grid by a nearest-neighbor interpolation. The surface covers approximately a 0.80 m by 0.25 m soil patch. Shadowed points (i.e., points that are not visible from the camera point of view due to the blockage of another, more elevated point in-between) are interpolated using a nearest-neighbor algorithm as well. Once the entire surface is rendered at 1 mm by 1 mm grid size, about 250 lengthwise transects (one per millimeter) are computed. Each transect is detrended separately to remove the mean profile height and profile tilt, thus correcting for any instrument misalignment in the experimental set-up. Thus, these detrended transects are used as 1-D profile samples of the surface random component.
A small barrel distortion (i.e., lens effect which causes straight lines to curve out) were detected in the calibration procedure in laboratory. It was observed on the top of the pictures, where only would affect terrain features of around 20 cm height. For typical soil elements (0–10 cm height), this distortion does not have any influence on measurements. In field measurements, standing crop residue has a contrasting height with respect to the points over the soil surface. Thus, height points from crop elements are identified as outliers by comparing the height of their nearest neighbors over the soil. Before the second processing stage, these outliers are disregarded. The presence of laid crop residue is more difficult to deal with. The impact of laid crop residue is reduced by selecting sites with a relative low amount of crop elements. It might be necessary to remove some crop residues by hand prior to instrument deployment.
2.2. Instrument Limitations
The limitations relative to both the finite dimensions and finite sampling interval of the measurement device can be analyzed by means of the power spectrum (i.e., the Fourier transform of the autocorrelation function) of the profile record. In effect, roughness measurements using profilers are always band-limited in the sense that they lay between a minimum and a maximum in the spatial frequency domain, being these determined by the profile length L and the sampling interval , respectively. For URSuLa, and , indicating the spatial frequency range of soil features which URSuLa is sensitive at.
Figure 3 depicts a power spectrum measured by URSuLa (profile length 800 mm and sampling interval 1 mm) corresponding to 10 single profiles averaged over the same field (Azul, February 2009; see
Section 2.4). From this average power spectrum, it turns out that the estimation of the low-frequency components is better than the high-frequency ones (
i.e.,
). This is due to the fact that low-frequency components are sampled at a larger density of points per frequency unit, since the sampling frequency URSuLa measures each roughness component in the soil profile is
. Yet, most of the shape of the small-scale spectrum is still captured by the laser profiler, constrained to the Nyquist sampling criterion
[
25]. Therefore, the laser profiler URSuLa is suited to estimate small-scale, random component roughness parameters
s and
l from 1-D profiles.
2.3. Roughness Descriptors
As mentioned in the Introduction, surface roughness conditions may be summarized using only two parameters derived from 1-D profiles: The surface height standard deviation
s, defined for a discretized, detrended profile of
n points as
where
is the height of the soil profile measured from the mean line at
, and the autocorrelation function
ρ at
ξ,
from which the correlation length
l, defined as the distance so that
, is computed. For stochastic surfaces,
approaches to 0 for
ξ approaching to infinity, indicating that beyond a certain distance, two surface points become uncorrelated. Also, the definition in Equation (
2) is normalized in such a way that
as
. The parameterization given in Equations (
1) and (
2) is only valid for the small-scale roughness. From each 3-D surface rendering, about 250 transects separated away one millimeter were used as 1-D profile samples. On each sample,
s and
l are computed and then averaged, leading to
N = 83 pairs (
s,
l) for this paper.
2.4. Field Work
In order to obtain a sound statistical sample of roughness conditions and to diminish the dependence of the results on a particular site, an extensive campaign was performed over three sites spread out on the Argentine’s Pampas—vast plains extending westward across central Argentina from the Atlantic coast to the Andean foothills and one of the major agricultural regions in the world. The main characteristics of the different fields are given in
Table 1. Azul site is managed by the National University of the Center of the Buenos Aires Province (UNICEN), CETT site belongs to the Argentine Space Agency (CONAE), whereas Bell Ville site belongs to a private farmer. Since Azul and CETT are test sites, the tillage management practice was experimentally set at the time the field work was done. In Bell Ville, management practice was exclusively decided by the owner. Azul site was visited twice in February and April (Azul F and Azul A) presenting ploughed (PLD) fields. CETT and Bell Ville were visited once, with three different tillages over several fields: ploughed and harrowed with disk (DSK) for CETT and seedbed (SBD) for Bell Ville. One of the CETT’s harrowed fields appeared clearly weathered (WTH) and was analyzed separately. In
Table 1 the farming activities prior to measurements are also reported. In Azul site, the tillage operations were done the day before the measurements were taken. The tillage operations in CETT site were done the week before and there were no rain events during that week. Still, somewhat of wind erosion was observed from a visual inspection in one of the harrowed field. The seedbed field in Bell Ville was done using a no-till planter the week before the measurements were taken, with no rain events during that week.
Figure 4 depicts the tillage conditions at the time the soil roughness measurements were done. Since tillage furrows were presented, only profiles parallel to tillage direction were used in this study.
2.5. Data Analysis
URSuLa is able to digitize a soil patch of 0.80 m by 0.25 m with the surface heights evenly sampled at a 1 mm by 1 mm grid size. This 3-D rendered surface is decomposed into 0.80 m-length transects which are detrended by a linear polynomial. Each detrended, lengthwise, 1-mm-sampling-interval transect is then undergone a moving average filter. In this process, a sequence of consecutive height points within a predefined window are averaged out and the resulting height is placed at the center position of the original sequence, thus synthesizing profiles at different sampling intervals according to the window length. Window lengths were chosen to span 2, 5, 10, 20 and 50 consecutive height points from 1-mm-sampling-interval profiles, thus mimicking profiles acquired by profiling techniques with different sampling intervals.
Once the processed profiles are at hand, roughness parameters height standard deviation
s, autocorrelation function and correlation length
l are computed and their dependence on the sampling interval are evaluated on a field basis (
i.e., roughness parameters are averaged out within each field). Comparison of experimental ACF with theoretical Gaussian and exponential models is also done. Then, the impact of the different sampling intervals on the separability of the different tillage conditions is assessed onto a (
s,
l)-plane. Finally, a theoretical electromagnetic scattering model is employed to identify the spatial scales more relevant to accurately account for the microwave response of a soil surface. This model, referred to as IEM2M [
23,
24], predicts co-polarized backscattering coefficients HH and VV from a random rough surface given its dielectric constant, roughness parameters and autocorrelation function, besides the observation geometry parameters frequency and beam incidence angle.
4. Discussion
Microwave backscatter response from agricultural surfaces depends on the arrangement and shape of the surface constituents at several spatial scales. When no coherent effect is observed, the random component of the surface roughness has the dominant contribution to the microwave response. The random component of surface soil roughness is estimated from 1-D profiles using two parameters that accounts for the vertical (s) and horizontal (l) roughness component. Non-contact profiling techniques such as laser triangulation, laser scanning or photogrammetry deal with a number of different sampling intervals, due to the diversity of experimental set-ups and to the technique itself.
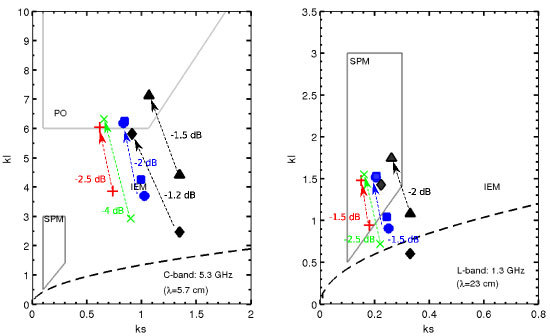
The enhanced technical capabilities of URSuLa (i.e., 1 mm sampling interval, an extended profiling area and multisite capability) enables an experimental study aimed to improve the understanding of the spatial scales involved in microwave backscattering of soil surfaces under different tillages. Within this context, the effect of sampling-interval-dependent roughness parameters on backscatter response at X-, C- and L-band was assessed through an experimental study of the dependence of the roughness descriptors on the sampling interval. Sampling intervals range from large (50 mm) to small (1 mm), with intermediate 20 mm, 10 mm, 5 mm and 2 mm intervals, thus covering a large number of profiling techniques. Large- and intermediate-sampling-interval profiles were synthetically derived from nominal, 1 mm ones and used to assess the variations of roughness parameters (s and l) depending on the sampling interval and their influence in soil surface backscatter response.
It was observed a dependency between
s and tillage activities in such a way that the more intensive the soil disturbance, the larger the
s values, in accordance to [
7,
8,
12,
30]. Regarding to the correlation length
l, dependency on tillage was somewhat less marked, possible due to the limited profile length of URSuLa in comparison to other profilers [
8]. In general, for the field medians, it was observed that the
s values decreased and the
l values increased as the sampling interval became coarser from 1 mm to 50 mm, which is a consequence of the smoothing effect of the low-pass filtering and of the finite lower band limit of URSuLa’s power spectrum. This led to less separable tillage classes in the sense of separability among clusters’ centers at coarse sampling intervals. Thus, it was highlighted the need for accurate measurements of the small scale components for discriminating among different tillage states. Also, it turned out that the uncertainties of these medians (
i.e., error bars in
Figure 6) are related to the variability within the fields, masking the influence of the different sampling intervals used. A direct relationship between
s and
l was found, where the results were in accordance to [
12] for a sampling interval of 5 mm and to [
27] for a sampling interval of 20 mm.
Regarding the ACF, the exponential ACF is characterized by smaller correlations at small lags compared to the Gaussian one. This causes that exponential ACFs to better describe the small-scale roughness in the profile than Gaussian ACFs [
16]. Thus, the loss of high-frequency roughness component as the sampling interval increased led to an overestimation of the correlation length
l, where the effect was more marked for the smooth roughness fields. Moreover, the small-scale components dominated the autocorrelation function for the medium roughness tillage states, where exponential correlation function agreed better with experimental ACF than the Gaussian case, with a poor agreement for the rougher fields nonetheless. This result is aligned with different studies in [
6,
7,
8,
16] that found the ACF was well approximated by exponential correlation function. For larger sampling intervals, a mixed behavior is observed, where the exponential type resembled more closely the experimental ACF for lags less than
l but the Gaussian type was slightly closer for lags greater than
l. Deviation from the exponential ACF especially at higher lags was also found in [
20]. Since exponential and Gaussian theoretical descriptions do not always describe the roughness of natural surfaces very well, more complex models for ACF can be found in [
31], where two analytical models introducing a varying power for the correlation function are suggested to fit the experimental ACF. Their shapes lie between the exponential and Gaussian cases, covering both types of ACFs, which might be useful for describing the intermediate shapes found in the 20-mm-sampling-interval ACFs. In view of the lack of similar studies systematically applied on real agricultural lands, the results presented here regarding the effect of the sampling interval can be combined to those describing the dependence of roughness parameters on profile length [
8], to contribute to a better understanding on the scaling issues of the roughness and its complex nature.
Simulations carried out by using the theoretical backscatter model IEM2M demonstrated that this effect depended on the working wavelength and that coarsely-sampled roughness parameters will lead to larger error at short wavelengths such as C-band than at larger ones such as L-band. These errors come from an underestimation of the high-frequency components presented in the smaller scales. For the three bands studied here, an underestimation of the backscattering coefficient of about 1–4 dB was observed at coarser sampling intervals. It was also found that could serve as an appropriate proxy to accounting for the relevant roughness components in the microwave backscattering response of soil surfaces. Selection of the profiling technique should rely on accurately characterize this surface component.