Next Article in Journal
Space Geodetic Observations and Modeling of 2016 Mw 5.9 Menyuan Earthquake: Implications on Seismogenic Tectonic Motion
Next Article in Special Issue
Increasing the Accuracy and Automation of Fractional Vegetation Cover Estimation from Digital Photographs
Previous Article in Journal
An Automated Approach for Sub-Pixel Registration of Landsat-8 Operational Land Imager (OLI) and Sentinel-2 Multi Spectral Instrument (MSI) Imagery
Previous Article in Special Issue
Abiotic Controls on Macroscale Variations of Humid Tropical Forest Height
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 8
Issue 6
10.3390/rs8060522
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Sensitivity of L-Band SAR Backscatter to Aboveground Biomass of Global Forests

by
Yifan Yu
* and
Sassan Saatchi
Jet Propulsion Laboratory, California Institue of Technology, Pasadena, CA 91109, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2016, 8(6), 522; https://doi.org/10.3390/rs8060522
Submission received: 1 May 2016 / Revised: 13 June 2016 / Accepted: 17 June 2016 / Published: 22 June 2016
(This article belongs to the Special Issue Remote Sensing of Vegetation Structure and Dynamics)
Browse Figures
Versions Notes

Abstract

:
Synthetic Aperture Radar (SAR) backscatter measurements are sensitive to forest aboveground biomass (AGB), and the observations from space can be used for mapping AGB globally. However, the radar sensitivity saturates at higher AGB values depending on the wavelength and geometry of radar measurements, and is influenced by the structure of the forest and environmental conditions. Here, we examine the sensitivity of SAR at the L-band frequency (~25 cm wavelength) to AGB in order to examine the performance of future joint National Aeronautics and Space Administration, Indian Space Research Organisation NASA-ISRO SAR mission in mapping the AGB of global forests. For SAR data, we use the Phased Array L-Band SAR (PALSAR) backscatter from the Advanced Land Observing Satellite (ALOS) aggregated at a 100-m spatial resolution; and for AGB data, we use more than three million AGB values derived from the Geoscience Laser Altimeter System (GLAS) LiDAR height metrics at about 0.16–0.25 ha footprints across eleven different forest types globally. The results from statistical analysis show that, over all eleven forest types, saturation level of L-band radar at HV polarization on average remains ≥100 Mg·ha−1. Fresh water swamp forests have the lowest saturation with AGB at ~80 Mg·ha−1, while needleleaf forests have the highest saturation at ~250 Mg·ha−1. Swamp forests show a strong backscatter from the vegetation-surface specular reflection due to inundation that requires to be treated separately from those on terra firme. Our results demonstrate that L-Band backscatter relations to AGB can be significantly different depending on forest types and environmental effects, requiring multiple algorithms to map AGB from time series of satellite radar observations globally.

Graphical Abstract

1. Introduction

Forests play an important role in the global carbon cycle both by storing carbon and by functioning as a sink for roughly a quarter of the annual anthropogenic emissions of carbon dioxide to the atmosphere [1,2]. The contribution of the global forests in the carbon cycle follows two trajectories: (1) deforestation and degradation that reduces the forest biomass from its original state at time t0 to a reduced state in the case of degradation and to approximately zero in the case of deforestation at time t1; (2) recovery through the process of regeneration and afforestation after time t1 towards its original state. These two trajectories are often related to human activities on changing the land use and land cover (LULC). Additionally, there is a natural cycle of disturbance and recovery in forests that contributes to global sources and sinks of carbon in forests by changing the biomass significantly [3]. Quantifying the aboveground biomass (AGB) of global forests and the changes from LULC activities has become an urgent task of the science community for reducing the uncertainty in global carbon cycle, and an important responsibility of the international community for reporting and assessing national scale carbon emissions and removals [1,4,5]. The global biomass in vegetation is distributed in different forest types or in a mosaic of shrubs and trees over landscapes with a large diversity of environmental characteristics (climate, soil, topography) and under different processes of disturbance and recovery [6,7,8]. However, forest biomass stocks and changes are not accurately quantified or mapped systematically except in regions of the northern hemisphere where national forest inventory samples are available [9,10,11]. In the absence of systematic and frequent inventory samples of global forests, remote sensing techniques are considered the most promising approach to provide up-to-date information on the status of forest cover and carbon stocks [6,12,13].
Among remote sensing techniques, radar sensors at long wavelengths have the advantage of sensitivity to forest AGB and the potential for high spatial and temporal resolution observations necessary for quantifying and monitoring carbon stocks at the scale where human activities occur [6,14,15]. However, the sensitivity of radar to AGB varies depending on the wavelength, which determines the penetration of the microwave energy into the canopy and the scattering from woody component of the forests and other factors related to the structure of forest and the landscape and the moisture of the underlying soil [16,17]. This sensitivity is often shown by correlating the radar backscatter to AGB at different polarizations and frequencies of P-band [18,19,20], L-band (~15–30 cm wavelength) [21,22], and C-band (~4–8 cm wavelength) [23,24]. It is generally understood that at shorter wavelengths of C-band radar, microwave energy attenuates quickly while traveling through the dense forest canopy before scattering from large woody components (stems and large branches). However, at longer wavelengths as in the L-band and P-band radar sensors, the attenuation is weaker and the backscattered energy carry information from large woody components, providing better correlation with AGB. A quick review of the literature suggests that the range of forest biomass sensitivity for L-band SAR backscatter measurements is 75–150 Mg·ha−1 [22,23,25,26,27], which can increase to about 300 Mg·ha−1 at P-band (~70–90 cm wavelength) [6,14,19,28,29]. In addition to backscatter sensitivity to AGB, radar sensors in interferometry configurations can provide estimates of the vertical structure of a forest, allowing an improved estimation of forest biomass and extending the sensitivity of radar sensing to higher ranges of AGB [30,31,32,33]. Based on these studies and numerous other publications, radar sensors have been selected by several space agencies as the sensor of choice for space observation of forest structure and biomass. By the early 2020s, the US National Aeronautic and Space Administration (NASA), Indian Space Research Organization (ISRO), and the European Space Agency (ESA) will, respectively, launch the L-band SAR NISAR (NASA ISRO SAR) and P-band SAR BIOMASS missions for monitoring forest structure and biomass. These two missions will add to a suite of other space-borne radar sensors, such as the Japanese Advanced Land Observing Satellite-2 (ALOS-2), the Phased Array L-band SAR-2 (PALSAR-2) and the Argentinean SAtélite Argentino de Observación COn Microondas SAOCOM, to improve global observations of forests.
In this study, we examine the sensitivity of L-band radar backscatter to AGB over global forests in order to assess the performance and limitations of space observations, such as the NISAR mission. NISAR will provide polarimetric observations every 12 days, globally, for ecosystem science. These observations are designed to capture the effect of environmental changes on the radar backscatter sensitivity to AGB, and allow annual mapping of AGB at a 100-m (1-ha) resolution globally. The science requirements for the mission is to map AGB at every 1-ha with less than 20 Mg·ha−1 or 20% accuracy, whichever is larger, for more than 80% of global forest areas with AGB range less than 100 Mg·ha−1. In addition, NISAR mission will map forest cover change from natural and anthropogenic disturbances and recovery at the same resolution every year. These requirements will be met by using an algorithm to retrieve AGB from the high-density time series observations repeated every 12 days. Here, we explore the sensitivity of L-band radar by addressing the following questions:
  • What is the overall sensitivity of L-band backscatter to AGB over global forests?
  • How many forest specific algorithms are required for global estimation of AGB?
  • What is the minimum number of radar observations required to estimate AGB annually?
We use the radar backscatter data from PALSAR, onboard the Advanced Land Observing Satellite (ALOS), from the Japan Aerospace Exploration Agency (JAXA), to simulate the NISAR observations. JAXA has released the 2007–2010 annual mosaics of ALOS PALSAR data at fine beam mode and dual polarizations of horizontal transmit/horizontal receive (HH) and horizontal transmit/vertical receive (HV) at 25 m resolution. They have also released the first ALOS2 mosaic at the same resolution for the 2015 period. We also make use of the Geoscience Laser Altimeter System (GLAS) onboard the Ice, Cloud, and land Elevation Satellite (ICESat) measurements of forest height and vertical structure, globally, to derive an estimate of forest biomass at the GLAS effective footprint size of approximately 50 m (0.25 ha). The footprint size changes depending on the lasers used for observation. We use these two data sets to simulate the L-band radar sensitivity to AGB across different forest types, globally. Note that, here, we are not interested in the estimation of the AGB and, hence, do not consider algorithmic approaches and impacts of structure and the landscape on the retrieval process.
The large sample size from GLAS and the global coverage from ALOS allow us to develop statistical approaches to examine the sensitivity of radar to AGB by filtering out many sources of noise in the data, including the environmental effects, to look at the underlying relationship between AGB and backscatter. The statistics derived from the analysis provide us with quantitative information to address the main questions about the sensitivity and requirements for global forest biomass estimation.

2. Materials and Methods

2.1. Remote Sensing Data

2.1.1. ALOS PALSAR

The Japanese Aerospace Exploration Agency’s (JAXA) Advanced Land Observing Satellite’s (ALOS) Phased Array L-band Synthetic Aperture Radar (PALSAR), operating at 1270 MHz, provides sensitivity to low to medium biomass forests [6,34]. Global mosaic of PALSAR backscatter measurements from the fine beam mode in dual polarization (HH, HV) at approximately 25 m pixel size has been released annually (2007–2010) by JAXA. The global mosaic is corrected for geometric distortion and topographic effects, but with significant distortions in areas of high slopes [35]. We use the HH and HV backscatter values from 2007 for this study. The backscatter digital numbers (DN) from the PALSAR product are first converted to backscatter coefficient (sigma-0) in units of decibel power (dB), then converted to linear power, and then aggregated to a 100-m resolution using simple averaging with a 4 × 4 window. This helps reduce the speckle noise in the radar backscatter, as well as the variance in forest structure, both of which increase significantly as plot size decreases below 1-ha [20]. No other processing was done on the PALSAR backscatter values. We use the linear power of sigma-0 for this study.

2.1.2. ICESat GLAS LiDAR

ICESat GLAS LiDAR is used extensively for the study of vegetation vertical structure [36,37,38,39]. The waveform from GLAS LiDAR return over forests contain information correlated with the Lorey’s height and mean canopy height of the forest over the LiDAR footprint [40]. We use methods described by Lefsky et al. [40] to estimate Lorey’s height from level 1A waveforms from GLAS. Lorey’s height is defined as:
H = ∑ i   =   1 N B A i h i ∑ i   =   1 N B A i
where H is Lorey’s height; BAi is the basal area (cross-sectional area of trunk at breast height, ~1.3 m from ground or above the tree irregularities) of the ith tree; hi is the total canopy height of the ith tree. Lorey’s height is calculated from the level 1A GLAS waveform using the extent, lead, and trail of the waveform. Lead and trail are the leading edge extent and trailing edge extent of the waveform, respectively. Extent is the height of the full waveform from the first return to the last return. Coefficients are developed for Lorey’s height as a linear regression of the above waveform metrics for three general forests of broadleaf, needleleaf, and mixed, using ground observations. Lorey’s height has been shown to have strong correlation with aboveground biomass of forests when the LiDAR footprint is fully covered by forest canopy [6,36].
Slope underneath the LiDAR footprint can also introduce errors to the estimation of Lorey’s height [40] due to the mixing of return signal from the underlying topography with returns from the canopy. While a slope-correction, based on the trailing edge of LiDAR waveform, was applied when calculating Lorey’s height [40], we additionally removed any GLAS shots that fall on terrains with slope greater than 20%. Slope is calculated using Exelis ENVI software with SRTM DEM as input. In addition, we filtered all waveforms with signal-to-noise-ratio of smaller than 50, and used the cloud flag in the GLAS GLA14 dataset to remove waveforms significantly impacted by clouds. Approximately 7 million GLAS shots were included in the analysis covering the GLAS operational periods 3A through 3J, which corresponds to October 2004 through March 2008. The effective footprint size of GLAS LiDAR Gaussian pulse for this period is variable but remains approximately bounded between 0.16 ha and 0.25 ha [41].

2.1.3. Landcover Maps

We use two different landcover maps for the separation of landcover types. These are the GlobCover product from the European Space Agency (ESA) for year 2005–2006 (Version 2.2) [42] and the World Wildlife Fund’s (WWF) 14-ecoregion map, published in 2001 [43]. GlobCover classifies the global landcover types into 22 different types at 300 m resolution using the Medium Resolution Imaging Spectrometer (MERIS) onboard ESA’s Envisat. The WWF ecoregion map divides the world into 14 biome types, and a further subdivision of 867 ecoregions. The 14 biome classification is used for this study.
GlobCover provides fine spatial scale classification of landcover types that are closer to the footprint size of GLAS LiDAR shots. However, it does not differentiate certain biome types; for example, temperate conifers and boreal conifers. The WWF map provides the general separation of biomes required for this study, but lacks the spatial resolution we need, and introduces noise into our analysis if used alone to separate GLAS shots. Therefore, we combine these two landcover maps to place each GLAS LiDAR shot into one of 11 categories of interest (Table 1).

2.2. AGB Estimation from GLAS

Allometric equations, separated by the WWF biomes [43], were developed previously between GLAS-based Lorey’s height and AGB [44]. The allometric equations use an exponential form of AGB = αHβ where H is the Lorey’s height and α and β are fitting coefficients. The fitting coefficients used are listed in Table S2. Not all continents and biomes have enough ground inventory plots to develop local allometric equations. However, for those cases, equations from similar biomes on other continents are used. The allometric models are developed from ground data and applied on the GLAS estimation of Lorey’s height. This approach allows us to use height biomass relationships developed for different forests types without considering the coincident measurements of LiDAR and inventory data. In this analysis, we are only interested to convert the GLAS measurements to forest aboveground biomass in a systematic approach. The errors from the biomass estimation and potential differences due to the lack of coincident observations will eventually appear in the spread of the points when compared with the radar data.
North American allometries are based on inventory data from the United States Forest Inventory and Analysis (FIA). Dry broadleaf and tropical conifer forest allometric equations are developed using Mexico’s national inventory data. Only mean canopy height is provided for the Mexico inventory, therefore, we use empirical relationship between GLAS Lorey’s height and mean canopy height to convert GLAS Lorey’s height to mean canopy height. The same was done for Russian forest inventory data. These relations were developed by using data from plots in similar forest types where both mean canopy height and Lorey’s height were available [44]. Tropical forest allometric equations are based on research plots spread across South America, Africa, and Southeast Asia. These plots were used by Saatchi et al. [6] to create tropical forest allometries, and include a correction factor based on airborne LiDAR shown in Figure S1. The estimates of AGB from the GLAS derived Lorey’s height is subject to different sources of errors: (1) measurement errors associated with the estimates of Lorey’s height from waveform metrics; (2) allometric errors converting the GLAS Lorey’s height to AGB; (3) location error associated with the geolocation of GLAS LiDAR shots on the ground; (4) errors associated with the land cover maps assigning the wrong allometry to the GLAS footprints; and (5) uncertainty in GLAS effective footprint size and discrepancy between GLAS footprint and the ground plots used in developing the AGB. In this study we do not intend to quantify these errors. However, the knowledge of sources of the errors can partially explain any variations detected when comparing the GLAS derived AGB with radar backscatter.

2.3. Methodology

GLAS LiDAR based Lorey’s height are first converted to AGB using allometric equations shown in Table S2. For each GLAS shot, we also extract the pixel value from GlobCover, WWF biome, and ALOS HH/HV backscatter using the latitude/longitude coordinate of the GLAS shot. Each AGB value now is associated with 2 landcover types and 2 ALOS backscatter values. These AGB values are further divided into forest categories using the rules stated in Table 1. The AGB values derived from GLAS LiDAR varies within each biome and landcover type from values greater than zero to above 600 Mg·ha−1. The values of ALOS radar measurements derived from the LiDAR footprint locations also spread over a large range of backscatter values reflecting differences in the size of LiDAR and radar pixels, geolocation errors, radar radiometric calibrations, differences in timing of ALOS PALSAR and GLAS LiDAR observations, impacts of environmental condition (soil moisture, pheneology) on radar backscatter, and all above-mentioned sources of errors associated with GLAS derived AGB.

2.3.1. Radar Biomass Models

To demonstrate the relations between radar measurements and AGB, we place the AGB values into 5 Mg·ha−1 bins and average the corresponding backscatter values. For every bin within each forest category, the mean and standard deviation of the ALOS HH and HV backscatter values (sigma-0) within the bin are calculated. The mid-AGB value is used to represent each bin. For example, for the bin of 100–105 Mg·ha−1, the mid-value of 102.5 Mg·ha−1 is used to represent this bin. Towards the higher biomass values, the number of points within each bin starts to decrease as the area of such forests decrease. We cut off the tail end of this bin distribution once the number of points within the bin falls below 500. Additionally, the lowest 2–3 bins typically contain erroneous shots, likely due to geolocation errors. These are removed as outliers based on the number of points as well as mean backscatter values compared to neighboring bins. In the case of tropical moist forests of South America, Africa, and Southeast Asia, the bins are cut-off at 155 Mg·ha−1 because saturation occurs early for these forest types and HV backscatter start to exhibit decreasing values as AGB increase higher, similar to what was observed by Mermoz et al. [27].
The HV polarization typically has better sensitivity to forest AGB than the HH polarization. A comparison between HH and HV polarization for the Africa and South America tropical moist forests are shown in the supplementary materials in Figure S2. Therefore, we focus this study on the HV polarization of ALOS PALSAR data. For each forest category, we fit an equation between the mean ALOS backscatter sigma-0 of the bin and the mid-bin AGB value. The equation is of the form:
σ 0 = A   x α   ( 1 −   e − B x ) + C
where x is AGB in Mg·ha−1; A, B, C, and α are fitting coefficients. When fitting the equations, only AGB bins up to 300 Mg·ha−1 are used (if enough AGB points exist, otherwise, it stops when the number of points within the bin first falls below 500), and up to 155 Mg·ha−1 for the case of tropical moist forests. The equation is fitted by minimizing chi-square, with the following constraints on the fit coefficients: A, B, C ≥ 0; 0 < α < 1. The standard deviation values for each bin are used to demonstrate the amount of variance at the pixel level when trying to infer AGB from ALOS backscatter. Here, we only concentrate on the model fits to the mean values of backscatter for each bin and ignore the uncertainty or noise in measurements or when observations deviate from the model due to heteroskedasticity. This approach is justified because: 1. we are only interested in exploring the radar sensitivity to AGB; 2. the noise or spread around the mean does not represent the “true” variations of the radar backscatter because we only use radar backscatter measurement separated in time and space from the AGB observation by LiDAR. Additionally, ALOS PALSAR data is only collected during a portion of the year and does not provide the seasonal variations in environmental factors such as soil moisture. The “true” radar backscatter measurements will have larger variability for low values of AGB due to more contribution from soil moisture, and relatively smaller variations when AGB increases due to saturation of L-band backscatter at high biomass values and less influence from soil moisture.
Equation (2) captures the volume scattering component of a typical radar backscatter model in vegetated surfaces [22,45,46] and leaves the other components, such as contributions from the soil surface in terms of direct surface scattering and surface–volume interactions as the contribution in C. This simplification is an approximation by assuming the dominant scattering contribution in HV polarization at L-band frequency is the volume scattering [16] and the sensitivity of SAR to forest biomass is dominated by the behavior of the volume scattering component.

2.3.2. Radar Sensitivity

The empirically fitted equations allow the calculation of the change in radar backscatter as a function of biomass by taking the derivative of Equation (2) with respect to biomass:
∂ σ 0 ∂ x = A α x α − 1 ( 1 − e − B x ) + A x α B e − B x
This equation can then be used to calculate the level of change in radar backscatter that is required to differentiate a given amount of change in AGB. We use Equation (3) to calculate radar sensitivity at each of the AGB bins by evaluating the derivative at the AGB value of the middle of the bin. The sensitivity required to detect a 20% change in AGB is calculated by approximating the derivative to be constant for this range, and calculate delta sigma-0 between +10% and −10% of the desired AGB level. To obtain delta sigma-0 in units of dB, we use the following relationship:
∂ σ 0 ( d B ) ∂ x = 10 ln ( 10 ) σ 0 ∂ σ 0 ∂ x
Equation (4) can be used with the values calculated from Equation (3) to obtain radar sensitivity levels in decibels. We also calculate radar sensitivity for detecting a constant change of AGB value of 20 Mg·ha−1 for the different levels of AGB by using the same method above except using ±10 Mg·ha−1 around the given AGB value. These correspond to 10 Mg·ha−1 uncertainty in AGB estimation which is 50% lower than NISAR requirement.

2.3.3. Radar Detection of Biomass

Estimating the number of observations for estimating AGB within 20 Mg·ha−1 uncertainty requires knowledge of the “true” variations of the L-band SAR observations at different biomass levels. This requires multi-temporal observations for L-band radar measurements at 100-m pixels represented by accurate ground-estimated AGB over the range of radar sensitivity. We do not have access to such data for global forests. Here, we assume that the average variations observed from comparing the AGB estimated at the GLAS LiDAR footprint is a conservative estimate of the “true” variations of radar backscatter. Our assumption of conservativeness is based on: 1. Existing data on temporal variability of L-band radar backscatter over the range of biomass shows backscatter variation gradually reduces at higher biomass values [22] and on the average is smaller than the variations from spatial analysis in this study [47]; and 2. The errors in difference in timing of GLAS and ALOS data and the geolocation errors can introduce large variability in backscatter-biomass relations. The variation due to these errors at high biomass regions is larger because of the contrast between radar backscatter from forest and non-forest pixels. This will occur when the GLAS shot of a forest falls in a deforested pixel on ALOS data because of the geolocation error or forest clearing from the time of GLAS observation. In areas of low biomass range the contrast between radar backscatter from a pixel of low biomass to one of non-forest is much smaller, causing less scatter in the data. However, the spatial and temporal variations of soil moisture in low biomass areas will cause larger scatter in ALOS backscatter.
In the absence of multi-temporal observations globally, we scale the variance to account for the enhanced effect of environmental variations at low AGB values and their reduced effect at high AGB values while keeping the average variance the same over the entire range. The scaling ramps down from a factor of 1.5 at the lowest AGB bin to 0.5 at the 100 Mg·ha−1 AGB bin.
Additionally, the GLAS LiDAR footprint (~50 m) is roughly ¼ the area of an ALOS PALSAR pixel (~100 m). Since there are roughly 4 LiDAR shots within each radar pixel, and we compare them directly one-to-one when estimating variance, we assume that the size mismatch increases the actual standard deviation by a factor of 2 on the average. In general, the effect of pixel mismatch may be larger depending on the heterogeneity of the forest. Therefore, we reduce the calculated standard deviation by a factor of 2 to compensate for pixel mismatch. Next, we assume that the noise reduces as the square root of the number of observations and find the number of observations that will reduce the standard error to the level needed to differentiate a 20 Mg·ha−1 change in AGB according to Equation (3) for the given bin. To calculate the number of radar observations required, we set the standard error in sigma-0 equal to the sigma-0 required to differentiate a change of 20 Mg·ha−1 in AGB using: S E = s n where SE is the standard error, s is the standard deviation, and n is the number of observations.

3. Results

3.1. GLAS-Based AGB and ALOS Backscatter

Noise level is extremely high when correlating AGB directly with radar backscatter as shown in Figure 1a. Many sources of error can contribute to this high level of noise at the pixel level: speckle noise in radar backscatter, error in GLAS-derived AGB, mismatch between ALOS pixel size and GLAS footprint size, geo-location errors between GLAS shots and ALOS pixels. With enough data points averaged, assuming a random distribution of the errors, the noise can be reduced to allow the underlying correlation between backscatter and AGB to be shown (Figure 1b). We demonstrate this process using the North American boreal forest as an example (Figure 1). The correlation between ALOS HV backscatter coefficient (sigma-0) and AGB is clearly visible when looking at the bin means of sigma-0 values. The bars represent ±1 standard deviation from the mean, and show the large amount of scatter at the individual shot level within each bin.
Different forest biomes also present differing correlations between radar backscatter and AGB. In Figure 2, we demonstrate the differing radar backscatter responses of various forest biomes using flooded forests and boreal forests as examples. Figure 2a shows two types of flooded forests (fresh water and saline water). The fresh water flooded forests are mainly from tropical swamp forests, such as the central Amazon region. Saline water flooded forests are the mangrove forests. Due to the small total area of mangroves, there are very few GLAS shots available, causing the use of 100 shots for each bin instead of the typical 500 in other forest types and the early cutoff in biomass range. In mangrove forests, the large amount of leaf coverage and the root structure that are above the waterline are likely responsible for the over-all lower backscatter values compared to the fresh-water flooded forests with extensive gaps and strong volume-surface interaction from inundated surface. Boreal forests (Figure 2b) also exhibit different backscattering characteristics. This is likely due to the different tree species, with their different branch/leaf structure found between the North American boreal forests and the Eurasian boreal forests. Boreal forests as a whole also exhibit a stronger over-all backscatter compared to the flooded forests (note the bare-ground backscatter levels at 0 AGB and the backscatter levels at high AGB). This is primarily due to the smaller attenuation of radar energy from needleleaf and sparse canopy structure and stronger scattering from tree stems.
We use the form of Equation (2) to fit the observations to each of the forest categories listed in Table 1 and show empirical fits for the tropical moist forests in the Americas, Africa, and Southeast Asia, as well as temperate conifer forests, in Figure 3. It is evident that even among the tropical moist forests, there are different model fits and different levels of sensitivity to AGB. Coefficients for the models are listed in Table 2. In African and South American tropical moist forests, as AGB increases above 200 Mg·ha−1, there is a visible decline in ALOS HV backscatter, as observed by Mermoz et al. [27]. There are also outliers for the tropical moist forests typically between 50 Mg·ha−1 and 100 Mg·ha−1 that are removed before performing functional fits and limiting the AGB bins to 155 Mg·ha−1 as shown in Figure 3. The saturation and subsequent decrease in HV backscatter can have undesired effects on the fitting coefficients. Since we are most interested in the radar sensitivity for forests mainly below 100 Mg·ha−1, it is better to only use bins below 155 Mg·ha−1 for the model fits for tropical forests. Empirical fits between mean ALOS HV backscatter and AGB for all forest categories are shown in Figure S3.

3.2. Sensitivity Analysis

Equations (3) and (4) are used to calculate the radar sensitivity required to detect a 20% change in AGB. The sensitivity level is calculated for the mean AGB value for each bin and each forest and results are plotted in Figure 4. Because the sensitivity requirements are calculated as a percentage of the AGB, lower AGB values have a higher detection requirement in terms of absolute value of biomass. For example, for an AGB value of 20 Mg·ha−1, 20% change requires the detection of 4 Mg·ha−1 change in biomass; whereas for an AGB value of 100 Mg·ha−1, 20% change requires the detection of 20 Mg·ha−1 change in biomass. Therefore, the increase and decrease in sensitivity is determined by the competing factors of less stringent requirement for the detection in absolute change of biomass vs. the decreased radar sensitivity as the average AGB of the forest increases, and vice versa. This explains the shapes of curves in Figure 4 that are not always monotonically decreasing with increasing AGB. Sensitivity requirements are also calculated for the detection of the change by a constant AGB level of 20 Mg·ha−1 (shown in Figure 5). Because the detection requirement is constant in terms of biomass, the sensitivity is monotonically decreasing with increasing biomass.

3.3. Required Number of Observations

The number of radar observations required for estimating AGB to within 20 Mg·ha−1 is calculated using the standard deviation in the HV backscatter sigma-0 using the approach discussed in the method section. The variation in backscatter within each bin reflects the sum of all sources of noise as no filtering was used when calculating the bin statistics. This should include more noise in addition to any speckle noise from the radar itself. We assume that the variations of radar backscatter due to environmental conditions and speckle noise will reduce as the square root of the number of observations and find the number of observations that will reduce the standard error to the level needed to differentiate a 20 Mg·ha−1 change in AGB according to Equation (3) for the given bin. The results are shown in Figure 6.

4. Discussion

4.1. Radar Backscatter Model

The results suggest that different forest types have different backscatter responses at L-band radar frequency. The first implication is that, in order to infer AGB from radar backscatter, different models must be applied to each forest type and the number of models depend on the extent the structural variability of forest types introduce significantly different radar backscatter. The physics underlying the differences in backscatter model is explained by the understanding of the electromagnetic wave propagation and scattering in the forest canopies [16,48,49]. In a two layer forest canopy model consisting of distinct crown and trunk regions, the distorted Born approximation can be used to decompose the backscattering coefficient into three dominant terms rising from first order multiple scattering contributions: Volume scattering, volume-surface double bounce scattering, and surface scattering [16]. The most important terms contributing to the backscatter are the volume and volume-surface terms, with the surface backscatter becoming more important as AGB approaches zero.
In Equation (2), the first term represents the volume backscatter and the constant C can be interpreted as the contribution from other terms related to surface moisture condition in terms of volume-surface interaction and the surface backscatter. The value of α determines how soon the function flattens out with respect to AGB. Higher values of α means the saturation levels are at higher AGB and vice versa. Therefore, we can obtain a general idea of relatively how early different forest types saturate in L-band radar by comparing the α values from Table 2.
In forests where the canopy is not as dense, such as the temperate conifers and boreal forests, L-band backscatter can possibly have significant contribution from the surface-volume term with potentially enhanced sensitivity to forest biomass and soil moisture [47]. We explore this possibility by fitting a functional form that includes volume-surface contribution as shown in Equation (5)
σ 0 = A   x α   ( 1 −   e − B x ) + C x β e − B x + D
where A, B, C, D, α, and β are fitting coefficients. We select temperate conifer forest as an example to demonstrate the effect of other scattering contribution because the observations with ALOS PALSAR HV and AGB from GLAS LiDAR showed the strongest sensitivity to biomass. The fitted function of Equation (5) is plotted alongside that of Equation (2) for the temperate conifer forests in Figure 7.
The figure shows that both Equations (2) and (5) do a good job of empirically fitting the observed data. Because of the highly complex non-linear nature of Equation (5) and the small number of fitting data points, the fitted coefficients have larger uncertainties as shown by the one-standard-deviation values of the fitted coefficients. While the more complex functional form of Equation (5) may be closer to the physical representation of the full backscattering mechanism, caution must be taken using these fitted coefficients to make physical interpretations because of limited number of observational diversity. A more representative model can be developed when measurements of other radar backscatter polarizations along with biomass and surface moisture conditions are available to better constrain the effects of different scattering contributions. However, because both Equations (2) and (5) do a reasonably good job of empirically representing the observations, and show strong agreement over the biomass range present in the forest type, either one can be used to examine the radar sensitivity to AGB. We use Equation (2) because it represents the dominant scattering, has a simpler form, and it can be used for all forest types regardless of the potential contribution from other scattering terms.

4.2. Backscatter Sensitivity to Biomass

The sensitivity of L-band radar to AGB is also different for different forest types. If we first ignore noises associated with radar backscatter, we can obtain theoretical requirements on radar backscatter when inferring AGB by looking at the derivative of radar backscatter with respect to AGB in the fitted functions. Requirements on backscatter noise levels can be calculated for desired level of AGB differentiation using the empirical equations. For example, to calculate the minimum allowable noise level to differentiate between 150 Mg·ha−1 and 100 Mg·ha−1 forests in the South America tropical moist forests, we take the difference in the sigma-0 values between those two AGB values and calculate the difference between the two sigma-0 values. The radar must be able to differentiate those two signal levels to be able to separate 150 Mg·ha−1 from 100 Mg·ha−1 in the associated forest type.
In cases where a downward trend in HV backscatter is observed with increasing AGB values in the tropical moist forests [27], the L-band radar sensitivity and the saturation level can occur earlier in the biomass range. This is because of the strong attenuation of the radar signal before reaching the ground. In this case, a single sigma-0 value from backscatter can possibly be mapped to two different AGB values. Without additional information, it may not be possible to determine the biomass value associated with the backscatter. However, this decrease in backscatter with increasing AGB values is very small compared to the entire range of backscatter values and only occur at very high AGB levels. This suggests that by limiting AGB retrievals from backscatter values to AGB < 100 Mg·ha−1, we will not run into an ambiguity of converting the backscatter values to AGB.

4.3. Anomaly in Radar Backscatter Sensitivity to AGB

While relating the radar backscatter to AGB values derived from GLAS LiDAR height metrics, we noticed anomalies in the relationship that appeared in most tropical moist forest regions, but was most apparent in the swamp (fresh water flooded) forests. These anomalies refer to the HV backscatter values dropping at some AGB values in the mid-range before increasing again and finally leveling off due to signal saturation. This can be easily seen in Figure 2a between 50 Mg·ha−1 and 150 Mg·ha−1. Further analysis of the data shows that the GLAS LiDAR AGB distribution also significantly decreases in this region when backscatter drops as shown in Figure 8. Several possible theories can explain this phenomenon, each with its associated implications in terms of ecology and/or radar backscatter models for the forest type:
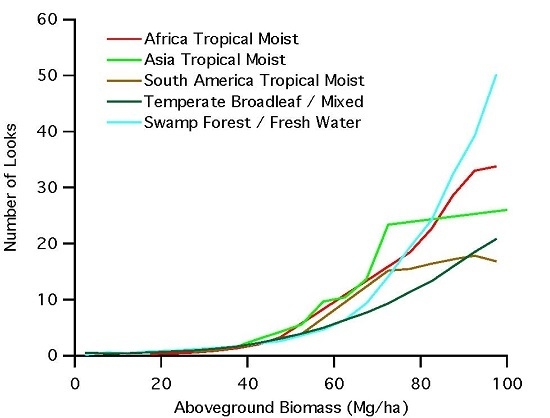
  • Assuming no errors in the GLAS LiDAR measurements over swamp forests, the results suggest a bi-modal distribution in terms of AGB. Since we can generally assume that GLAS is a systematic measurement of the surface, then the histogram of point distribution within each AGB bin can be interpreted as the frequency of occurrence of this particular AGB-class within the given forest type. The bi-modal distribution suggests that there may be two types of swamp forests with low and high average biomass density, and with very few areas transitioning between the two forest types. Although each type has a distribution around the mean value (~40 Mg·ha−1 for low biomass swamps and ~175 Mg·ha−1 for high biomass swamps), the two swamp forests are distinct in their biomass values.
  • The discontinuity in radar backscatter between these two modes also points to some different physical and/or environmental conditions between the two forest types giving rise to significantly different scattering responses. The responses may be associated with two different inundation cycles or seasonal variations in water level with the low biomass swamp forests coinciding with high inundation state and high biomass swamps under a lower inundation state, creating a bi-modal behavior in the radar backscatter. In addition, here, we are only considering the HV backscatter with the low sensitivity to inundation state. There is a high possibility that HV backscatter is capturing a strong volume-surface scattering in low biomass swamps and then transitioning to the regular HV biomass relationship to high biomass swamps.
  • There is also the possibility of GLAS measurements are erroneous in swamp forests with high-level inundation. Water has a strong absorption of the near-infrared wavelength used by GLAS. If enough of the surface under the forest is inundated with water, the GLAS LiDAR observation may experience very weak return from the surface and erroneously assume sub-canopy returns to be ground returns, and hence underestimating the canopy height. This would have an effect of shifting points in the affected areas into bins to the left (smaller AGB). The result of such shift would be an increase in the average sigma-0 of the lower bins (HV backscatter is not affected by the same mechanism), and a decrease in the number of points in the bins that the GLAS shots were shifted away from. However, this would also suggest that the same effect is not observed or is as pronounced in high biomass swamp forests. Otherwise, everything would shift to the left together there would not be a discontinuity in the AGB values that suggest that this may not be the right explanation of the discontinuity in the AGB values. To further explore the cause of this behavior in the radar backscatter, studies that include ground measurements of forest biomass and multi-temporal radar observations at different inundation state may be required.

4.4. GLAS Lidar Derived AGB

We assumed that the GLAS LiDAR derived AGB values from models developed over different forest types globally represent the true AGB. As we are not interested in estimation of AGB from radar, we did not include any uncertainty analysis of LiDAR derived AGB. In general, the random errors associated with LiDAR AGB estimates contribute to the overall variations of the radar backscatter and AGB, as shown in Figure 1a. In developing models based on radar backscatter and AGB, ground or LiDAR estimates are carefully quantified and represent the local variations of AGB, and therefore, introduce less scatter in radar biomass relations [20,25]. If the LiDAR AGB models are biased and over or underestimate AGB for a forest type, the errors introduced in radar biomass relationship may be larger and vary with biomass range. Additionally, in areas where uncertainty associated with LiDAR, as well as radar, tend to be higher; such as areas of high topography, the actual saturation level will be at lower AGB than what is estimated based on areas with more ideal conditions. However, even in the case of a biased LiDAR AGB estimates, the sensitivity analysis performed here is still valid and may be considered a conservative approach. It is conceivable to assume that with improved uncertainty associated with LiDAR derived AGB and other potential errors in AGB values compared with the radar backscatter, the sensitivity of L-band radar to biomass will be improved, and the number of observations to estimate AGB within the required uncertainty will reduce.

5. Conclusions

We use GLAS derived AGB values to empirically observe the L-band backscattering characteristics across eleven different forest biomes globally. Each biome exhibits different backscattering and associated saturation levels. Therefore, it is important that forest types are considered separately when using L-band radar backscatter to study AGB. Our empirically based radar backscatter models within these 11 different forest types suggest that L-band radar saturation level is greater than 100 Mg·ha−1 on the average with boreal forests and temperate conifers having an enhanced sensitivity to forest biomass reaching values >200 Mg·ha−1. Our study also explored the level of observational accuracy required to separate forest biomass values up to 100 Mg·ha−1. To infer forest AGB from L-band radar backscatter, it is also important to classify the area of interest into different forest types and use different algorithmic models to infer forest biomass. The number of observations required to differentiate a change of 20 Mg·ha−1 (±10 Mg·ha−1) in AGB up to 100 Mg·ha−1 for all 11 forest types suggests that only through multi-temporal observations, an accurate estimate of AGB from L-band radar backscatter is possible. Using L-band backscatter polarization diversity, such as including fully polarimetric measurements will potentially improve the estimation of the aboveground biomass. However, our study suggests that frequent observations would still be important to account for the variations associated with soil moisture and phenology. Therefore, space-borne missions, such as NISAR with high frequency of observations with minimum of dual polarizations (HH and HV), can produce reliable estimates of forest biomass up to 100 Mg·ha−1 over global forests by meeting the required uncertainty levels.

Supplementary Materials

The following are available online at www.mdpi.com/2072-4292/8/6/522/s1, Figure S1: Comparison of Lorey’s height derived from small-footprint DRL and derived from co-located GLAS shots over tropical forest. The scatter plot shows an under-estimation by GLAS of Lorey’s height in this forest type, Figure S2: Comparing ALOS HH and HV polarization sensitivity to AGB for (a) tropical moist forests of South America; and (b) boreal forest of North America . Mean sigma-0 values from AGB bins are calculated and plotted against the middle AGB value of the bin. Blue lines are for HH polarization and red lines are for HV polarization. Black bars show the total number of points in each AGB bin, Figure S3: Empirical fit between AGB and ALOS HV sigma-0 backscatter values for all forest categories. The categories are: (a) Latin America Tropical Moist; (b) Africa Tropical Moist; (c) Asia Tropical Moist; (d) Temperate Conifer; (e) North America Boreal; (f) Eurasia Boreal; (g) Fresh Water Flooded; (h) Saline Water Flooded; (i) Tropical Shrubland; (j) Tropical Dry Broadleaf. Table S1: GlobCover Classes used and their corresponding landcover type name. Table S2: List of allometric equations used to convert GLAS LiDAR-derived Lorey’s height to AGB {Yu:wz}. Equation is of the form AGB = α Hβ, where H is Lorey’s height.

Acknowledgments

This work was performed at the Jet Propulsion Laboratory, California Institute of Technology, under contract from National Aeronautic and Space Administration, as part of the NASA grant for NISAR science team member for biomass algorithm development (209249.04.01.01.19).

Author Contributions

Sassan Saatchi and Yifan Yu conceived and designed the study; Yifan Yu performed the data analysis; Yifan Yu and Sassan Saatchi wrote the paper.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
ALOSAdvanced Land Observing Satellite
PALSARPhased Array L-band Synthetic Aperture Radar
GLASGeoscience Laser Altimeter System
AGBAboveground Biomass
SARSynthetic Aperture Radar
LiDARLight Detection and Ranging
WWFWorld Wildlife Fund
DRLDiscrete Return LiDAR
NASANational Aeronautics and Space Administration
ISROIndian Space Research Organization
ESAEuropean Space Agency
NISARNASA ISRO SAR

References

  1. Houghton, R.A.; Hall, F.; Goetz, S.J. Importance of biomass in the global carbon cycle. J. Geophys. Res. 2009, 114, G00E03. [Google Scholar] [CrossRef]
  2. Le Quéré, C.; Moriarty, R.; Andrew, R.M.; Canadell, J.G.; Sitch, S.; Korsbakken, J.I.; Friedlingstein, P.; Peters, G.P.; Andres, R.J.; Boden, T.A.; et al. Global carbon budget 2015. Earth Syst. Sci. Data 2015, 7, 349–396. [Google Scholar] [CrossRef] [Green Version]
  3. Frolking, S.; Palace, M.W.; Clark, D.B.; Chambers, J.Q.; Shugart, H.H.; Hurtt, G.C. Forest disturbance and recovery: A general review in the context of spaceborne remote sensing of impacts on aboveground biomass and canopy structure. J. Geophys. Res. 2009, 114, G00E02. [Google Scholar] [CrossRef]
  4. Harris, N.L.; Brown, S.; Hagen, S.C.; Saatchi, S.S.; Petrova, S. Baseline map of carbon emissions from deforestation in tropical regions. Science 2012, 336, 1573–1576. [Google Scholar] [CrossRef] [PubMed]
  5. Gibbs, H.K.; Brown, S.; Niles, J.O.; Foley, J.A. Monitoring and estimating tropical forest carbon stocks: Making REDD a reality. Environ. Res. Lett. 2007, 2, 045023. [Google Scholar] [CrossRef]
  6. Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed]
  7. FAO. Global Forest Resources Assessment 2010—Main Report; FAO Forestry: Rome, Italy, 2010. [Google Scholar]
  8. Keith, H.; Mackey, B.G.; Lindenmayer, D.B. Re-evaluation of forest biomass carbon stocks and lessons from the world’s most carbon-dense forests. Proc. Natl. Acad. Sci. USA 2009, 106, 11635–11640. [Google Scholar] [CrossRef] [PubMed]
  9. Schimel, D.; Stephens, B.B.; Fisher, J.B. Effect of increasing CO2 on the terrestrial carbon cycle. Proc. Natl. Acad. Sci. USA 2015, 112, 436–441. [Google Scholar] [CrossRef] [PubMed]
  10. Saatchi, S.; Mascaro, J.; Xu, L.; Keller, M.; Yang, Y.; Duffy, P.; Espírito Santo, F.; Baccini, A.; Chambers, J.; Schimel, D. Seeing the forest beyond the trees. Glob. Ecol. Biogeogr. 2015, 24, 606–610. [Google Scholar] [CrossRef]
  11. Woodall, C.W.; Heath, L.S.; Domke, D.M.; Nichols, M.C. Methods and Equations for Estimating Aboveground Volume, Biomass, and Carbon for Trees in the US Forest Inventory, 2010; U.S. Forest Service: Washington, DC, USA, 2011. [Google Scholar]
  12. Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
  13. Thurner, M.; Beer, C.; Santoro, M.; Carvalhais, N.; Wutzler, T.; Schepaschenko, D.; Shvidenko, A.; Kompter, E.; Ahrens, B.; Levick, S.R.; et al. Carbon stock and density of northern boreal and temperate forests. Glob. Ecol. Biogeogr. 2014, 23, 297–310. [Google Scholar] [CrossRef]
  14. Le Toan, T.; Quegan, S.; Davidson, M.W.J.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H.; et al. The BIOMASS mission: Mapping global forest biomass to better understand the terrestrial carbon cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
  15. Mitchard, E.T.A.; Saatchi, S.S.; Woodhouse, I.H.; Nangendo, G.; Ribeiro, N.S.; Williams, M.; Ryan, C.M.; Lewis, S.L.; Feldpausch, T.R.; Meir, P. Using satellite radar backscatter to predict above-ground woody biomass: A consistent relationship across four different African landscapes. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
  16. Saatchi, S.S.; McDonald, K.C. Coherent effects in microwave backscattering models for forest canopies. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1032–1044. [Google Scholar] [CrossRef]
  17. Du, Y.; Ulaby, F.T.; Dobson, M.C. Sensitivity to soil moisture by active and passive microwave sensors. IEEE Trans. Geosci. Remote Sens. 2000, 38, 105–114. [Google Scholar] [CrossRef]
  18. Santos, J.R.; Freitas, C.C.; Araujo, L.S.; Dutra, L.V.; Mura, J.C.; Gama, F.F.; Soler, L.S.; SantAnna, S.J.S. Airborne P-band SAR applied to the aboveground biomass studies in the Brazilian tropical rainforest. Remote Sens. Environ. 2003, 87, 482–493. [Google Scholar] [CrossRef]
  19. Sandberg, G.; Ulander, L.M.H.; Fransson, J.E.S.; Holmgren, J.; Le Toan, T. L- and P-band backscatter intensity for biomass retrieval in hemiboreal forest. Remote Sens. Environ. 2011, 115, 2874–2886. [Google Scholar] [CrossRef]
  20. Saatchi, S.; Marlier, M.; Chazdon, R.L.; Clark, D.B.; Russell, A.E. Impact of spatial variability of tropical forest structure on radar estimation of aboveground biomass. Remote Sens. Environ. 2011, 115, 2836–2849. [Google Scholar] [CrossRef]
  21. Lucas, R.; Armston, J.; Fairfax, R.; Fensham, R.; Accad, A.; Carreiras, J.; Kelley, J.; Bunting, P.; Clewley, D.; Bray, S. An evaluation of the ALOS PALSAR L-band backscatter—Above ground biomass relationship Queensland, Australia: Impacts of surface moisture condition and vegetation structure. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2010, 3, 576–593. [Google Scholar] [CrossRef]
  22. Cartus, O.; Santoro, M.; Kellndorfer, J. Mapping forest aboveground biomass in the Northeastern United States with ALOS PALSAR dual-polarization L-band. Remote Sens. Environ. 2012, 124, 466–478. [Google Scholar] [CrossRef]
  23. Dobson, M.C.; Ulaby, F.T.; LeToan, T.; Beaudoin, A.; Kasischke, E.S.; Christensen, N. Dependence of radar backscatter on coniferous forest biomass. IEEE Trans. Geosci. Remote Sens. 1992, 30, 412–415. [Google Scholar] [CrossRef]
  24. Pulliainen, J.T.; Kurvonen, L.; Hallikainen, M.T. Multitemporal behavior of L- and C-band SAR observations of boreal forests. IEEE Trans. Geosci. Remote Sens. 1999, 37, 927–937. [Google Scholar] [CrossRef]
  25. Robinson, C.; Saatchi, S.; Neumann, M.; Gillespie, T. Impacts of spatial variability on aboveground biomass estimation from L-band radar in a temperate forest. Remote Sens. 2013, 5, 1001–1023. [Google Scholar] [CrossRef]
  26. Neumann, M.; Saatchi, S.S.; Ulander, L.M.H.; Fransson, J.E.S. Assessing Performance of L- and P-Band Polarimetric Interferometric SAR Data in Estimating Boreal Forest Above-Ground Biomass. IEEE Trans. Geosci. Remote Sens. 2012, 50, 714–726. [Google Scholar] [CrossRef]
  27. Mermoz, S.; Réjou-Méchain, M.; Villard, L.; Le Toan, T.; Rossi, V.; Gourlet-Fleury, S. Decrease of L-band SAR backscatter with biomass of dense forests. Remote Sens. Environ. 2015, 159, 307–317. [Google Scholar] [CrossRef]
  28. Hoekman, D.H.; Quiriones, M.J. Land cover type and biomass classification using AirSAR data for evaluation of monitoring scenarios in the Colombian Amazon. IEEE Trans. Geosci. Remote Sens. 2000, 38, 685–696. [Google Scholar] [CrossRef]
  29. Saatchi, S.S.; Houghton, R.A.; Alvala, R.C.; Soares, J.V.; Yu, Y. Distribution of aboveground live biomass in the Amazon basin. Glob. Chang. Biol. 2007, 13, 816–837. [Google Scholar] [CrossRef]
  30. Papathanassiou, K.P.; Cloude, S.R. Single-baseline polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2352–2363. [Google Scholar] [CrossRef]
  31. Cloude, S.R. Dual-baseline coherence tomography. IEEE Geosci. Remote Sens. Lett. 2007, 4, 127–131. [Google Scholar] [CrossRef]
  32. Balzter, H. Forest mapping and monitoring with interferometric synthetic aperture radar (InSAR). Prog. Phys. Geogr. 2001, 25, 159–177. [Google Scholar] [CrossRef]
  33. Hajnsek, I.; Kugler, F.; Lee, S.K.; Papathanassiou, K.P. Tropical-forest-parameter estimation by means of Pol-InSAR: The INDREX-II campaign. IEEE Trans. Geosci. Remote Sens. 2009, 47, 481–493. [Google Scholar] [CrossRef]
  34. Mitchard, E.T.A.; Saatchi, S.S.; White, L.J.T.; Abernethy, K.A.; Jeffery, K.J.; Lewis, S.L.; Collins, M.; Lefsky, M.A.; Leal, M.E.; Woodhouse, I.H.; et al. Mapping tropical forest biomass with radar and spaceborne LiDAR: Overcoming problems of high biomass and persistent cloud. Biogeosci. Discuss. 2011, 8, 8781–8815. [Google Scholar] [CrossRef]
  35. Shimada, M.; Ohtaki, T. Generating large-scale high-quality SAR Mosaic datasets: Application to PALSAR data for global monitoring. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2010, 3, 637–656. [Google Scholar] [CrossRef]
  36. Lefsky, M.A. A global forest canopy height map from the moderate resolution imaging spectroradiometer and the geoscience laser altimeter system. Geophys. Res. Lett. 2010, 37, L15401. [Google Scholar] [CrossRef]
  37. Los, S.O.; Rosette, J.A.B.; Kljun, N.; North, P.R.J.; Chasmer, L.; Suárez, J.C.; Hopkinson, C.; Hill, R.A.; van Gorsel, E.; Mahoney, C.; et al. Vegetation height and cover fraction between 60°S and 60°N from ICESat GLAS data. Geosci. Model. Dev. 2012, 5, 413–432. [Google Scholar] [CrossRef]
  38. Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. 2011, 116, G04021. [Google Scholar] [CrossRef]
  39. Neigh, C.S.R.; Nelson, R.F.; Ranson, K.J.; Margolis, H.A.; Montesano, P.M.; Sun, G.; Kharuk, V.; Næsset, E.; Wulder, M.A.; Andersen, H.-E. Taking stock of circumboreal forest carbon with ground measurements, airborne and spaceborne LiDAR. Remote Sens. Environ. 2013, 137, 274–287. [Google Scholar] [CrossRef]
  40. Lefsky, M.A.; Keller, M.; Pang, Y.; De Camargo, P.B.; Hunter, M.O. Revised method for forest canopy height estimation from Geoscience Laser Altimeter System waveforms. J. Appl. Remote Sens. 2007, 1, 013537. [Google Scholar]
  41. Popescu, S.C.; Zhao, K.; Neuenschwander, A.; Lin, C. Satellite LIDAR vs. small footprint airborne LIDAR: Comparing the accuracy of aboveground biomass estimates and forest structure metrics at footprint level. Remote Sens. Environ. 2011, 115, 2786–2797. [Google Scholar] [CrossRef]
  42. Arino, O.; Bicheron, P.; Achard, F.; Latham, J.; Witt, R.; Weber, J.-L. GLOBCOVER—The most detailed portrait of Earth. ESA Bull. Eur. Space Agency 2008, 136, 24–31. [Google Scholar]
  43. Olson, D.M.; Dinerstein, E.; Wikramanayake, E.D.; Burgess, N.D.; Powell, G.V.N.; Underwood, E.C.; D’amico, J.A.; Itoua, I.; Strand, H.E.; Morrison, J.C. Terrestrial ecoregions of the world: A new map of life on earth. BioScience 2001, 51, 933–938. [Google Scholar] [CrossRef]
  44. Yu, Y. Global Distribution of Carbon Stock in Live Woody Vegetation; University of California, Los Angeles: Los Angeles, CA, USA.
  45. Saatchi, S.; Moghaddam, M. Estimation of crown and stem water content and biomass of boreal forest using polarimetric SAR imagery. IEEE Trans. Geosci. Remote Sens. 2000, 38, 697–709. [Google Scholar] [CrossRef]
  46. Askne, J.; Santoro, M.; Smith, G.; Fransson, J.E.S. Multitemporal repeat-pass SAR interferometry of boreal forests. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1540–1550. [Google Scholar] [CrossRef]
  47. Hensley, S.; Oveisgharan, S.; Saatchi, S.; Simard, M.; Ahmed, R.; Haddad, Z. An error model for biomass estimates derived from polarimetric radar backscatter. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4065–4082. [Google Scholar] [CrossRef]
  48. Chauhan, N.S.; Lang, R.H.; Ranson, K.J. Radar modeling of a boreal forest. IEEE Trans. Geosci. Remote Sens. 1991, 29, 627–638. [Google Scholar] [CrossRef]
  49. Karam, M.A.; Fung, A.K.; Lang, R.H.; Chauhan, N.S. A microwave scattering model for layered vegetation. IEEE Trans. Geosci. Remote Sens. 1992, 30, 767–784. [Google Scholar] [CrossRef]
Remotesensing 08 00522 g001 1024
Figure 1. Correlation between GLAS-derived AGB (Mg·ha−1) and ALOS backscatter coefficient sigma-0 for North American boreal forest. (a) shows all GLAS shots and corresponding sigma-0 values from the pixel that the GLAS shot falls on; (b) shows the mean (circle) and ±1 standard deviation (bar) of ALOS HV sigma-0 values by binning the shots into 5 Mg·ha−1 bins. Bins below 10 Mg·ha−1 and above 235 Mg·ha−1 are removed as outliers.
Figure 1. Correlation between GLAS-derived AGB (Mg·ha−1) and ALOS backscatter coefficient sigma-0 for North American boreal forest. (a) shows all GLAS shots and corresponding sigma-0 values from the pixel that the GLAS shot falls on; (b) shows the mean (circle) and ±1 standard deviation (bar) of ALOS HV sigma-0 values by binning the shots into 5 Mg·ha−1 bins. Bins below 10 Mg·ha−1 and above 235 Mg·ha−1 are removed as outliers.
Remotesensing 08 00522 g001
Remotesensing 08 00522 g002 1024
Figure 2. Correlation between bin-averaged ALOS HV backscatter sigma-0 (m2·m−2) and middle of bin AGB value (Mg·ha−1) for (a) flooded forests; and (b) boreal forests. Outlier bins (such as some low bin values below 10 Mg·ha−1, and higher bins when the number of shots within the bin drop below 500, or 100 for the case of saline water flooded forests) are dropped. The flooded forests in (a) are divided into fresh-water and saline water (mangroves); boreal forests in (b) are divided by continent into North American boreal and Eurasian boreal.
Figure 2. Correlation between bin-averaged ALOS HV backscatter sigma-0 (m2·m−2) and middle of bin AGB value (Mg·ha−1) for (a) flooded forests; and (b) boreal forests. Outlier bins (such as some low bin values below 10 Mg·ha−1, and higher bins when the number of shots within the bin drop below 500, or 100 for the case of saline water flooded forests) are dropped. The flooded forests in (a) are divided into fresh-water and saline water (mangroves); boreal forests in (b) are divided by continent into North American boreal and Eurasian boreal.
Remotesensing 08 00522 g002
Remotesensing 08 00522 g003 1024
Figure 3. Correlation between bin-averaged ALOS HV sigma-0 means and AGB values of the middle of the bin for the tropical moist forests of Africa, Southeast Asia, and Latin America, as well as temperature conifer forests. Solid lines represent the empirically fitted function of the form defined in Equation (2). Certain outliers were removed before fitting for the tropical moist forest (marked with x). Bins for tropical forests are cut off above 155 Mg·ha−1 for the purpose of fitting.
Figure 3. Correlation between bin-averaged ALOS HV sigma-0 means and AGB values of the middle of the bin for the tropical moist forests of Africa, Southeast Asia, and Latin America, as well as temperature conifer forests. Solid lines represent the empirically fitted function of the form defined in Equation (2). Certain outliers were removed before fitting for the tropical moist forest (marked with x). Bins for tropical forests are cut off above 155 Mg·ha−1 for the purpose of fitting.
Remotesensing 08 00522 g003
Remotesensing 08 00522 g004 1024
Figure 4. Radar sensitivity required to detect a 20% change in AGB. The sensitivity requirement is calculated using Equations (3) and (4). The values for each bin are calculated using the derivatives from Equations (3) and (4) at the middle AGB value for each bin and ±10% from that middle AGB value. A total of 10 forest types are distinguished here, for better visibility, they are plotted in two separate figures: (a) Africa tropical moist broadleaf, South America tropical moist broadleaf, Asia tropical moist broadleaf, swamp forest/fresh water, mangrove/saline water (b) temperate conifer, Eurasia boreal, North America boreal, tropical savanna/shrub, and tropical dry broadleaf.
Figure 4. Radar sensitivity required to detect a 20% change in AGB. The sensitivity requirement is calculated using Equations (3) and (4). The values for each bin are calculated using the derivatives from Equations (3) and (4) at the middle AGB value for each bin and ±10% from that middle AGB value. A total of 10 forest types are distinguished here, for better visibility, they are plotted in two separate figures: (a) Africa tropical moist broadleaf, South America tropical moist broadleaf, Asia tropical moist broadleaf, swamp forest/fresh water, mangrove/saline water (b) temperate conifer, Eurasia boreal, North America boreal, tropical savanna/shrub, and tropical dry broadleaf.
Remotesensing 08 00522 g004
Remotesensing 08 00522 g005 1024
Figure 5. Radar sensitivity required to detect a 20 Mg·ha−1 change in AGB. The sensitivity requirement is calculated using Equations (3) and (4). The values for each bin are calculated using the derivatives from Equations (3) and (4) at the middle AGB value for each bin and ±10 Mg·ha−1 from that middle AGB value. A total of 10 forest types are distinguished here, for better visibility, they are plotted in two separate figures: (a) Africa tropical moist broadleaf, South America tropical moist broadleaf, Asia tropical moist broadleaf, swamp forest/fresh water, mangrove/saline water; (b) temperate conifer, Eurasia boreal, North America boreal, tropical savanna/shrub, and tropical dry broadleaf.
Figure 5. Radar sensitivity required to detect a 20 Mg·ha−1 change in AGB. The sensitivity requirement is calculated using Equations (3) and (4). The values for each bin are calculated using the derivatives from Equations (3) and (4) at the middle AGB value for each bin and ±10 Mg·ha−1 from that middle AGB value. A total of 10 forest types are distinguished here, for better visibility, they are plotted in two separate figures: (a) Africa tropical moist broadleaf, South America tropical moist broadleaf, Asia tropical moist broadleaf, swamp forest/fresh water, mangrove/saline water; (b) temperate conifer, Eurasia boreal, North America boreal, tropical savanna/shrub, and tropical dry broadleaf.
Remotesensing 08 00522 g005
Remotesensing 08 00522 g006 1024
Figure 6. Number of radar observations required to observe a 20 Mg·ha−1 change in AGB for various forest types. Values are calculated for each bin using the standard error in HV backscatter sigma-0 values to represent the amount of noise expected. For tropical savanna/shrubland (b), the number of looks is only calculated up to the AGB bin where enough data points are available. Forest types shown in (a) use a different y-axis scale as those shown in (b) due to the much lower observation requirements for the forests included in (b).
Figure 6. Number of radar observations required to observe a 20 Mg·ha−1 change in AGB for various forest types. Values are calculated for each bin using the standard error in HV backscatter sigma-0 values to represent the amount of noise expected. For tropical savanna/shrubland (b), the number of looks is only calculated up to the AGB bin where enough data points are available. Forest types shown in (a) use a different y-axis scale as those shown in (b) due to the much lower observation requirements for the forests included in (b).
Remotesensing 08 00522 g006
Remotesensing 08 00522 g007 1024
Figure 7. Average sigma-0 values (m2·m−2) for temperate conifer forests within 5 Mg·ha−1 biomass bins. Red line is the fitted function using Equation (5) (with surface-volume scattering term) while green line is the fitted function using Equation (2) (with only canopy volume scattering term). The coefficients shown are those fitted for Equation (5) with ±1 standard deviation.
Figure 7. Average sigma-0 values (m2·m−2) for temperate conifer forests within 5 Mg·ha−1 biomass bins. Red line is the fitted function using Equation (5) (with surface-volume scattering term) while green line is the fitted function using Equation (2) (with only canopy volume scattering term). The coefficients shown are those fitted for Equation (5) with ±1 standard deviation.
Remotesensing 08 00522 g007
Remotesensing 08 00522 g008 1024
Figure 8. Statistical analysis for freshwater flooded forest category. Red markers are the bin-averaged ALOS HV sigma-0 values. Green histogram shows the total number of GLAS shots within each bin.
Figure 8. Statistical analysis for freshwater flooded forest category. Red markers are the bin-averaged ALOS HV sigma-0 values. Green histogram shows the total number of GLAS shots within each bin.
Remotesensing 08 00522 g008
Table
Table 1. List of combination of World Wildlife Fund’s (WWF) biome and GlobCover landcover type used to determine forest categories that GLAS LiDAR shots belong to.
Table 1. List of combination of World Wildlife Fund’s (WWF) biome and GlobCover landcover type used to determine forest categories that GLAS LiDAR shots belong to.
WWF BiomeGlobCover *Category
Tropical Moist Broadleaf40Americas Tropical Moist
Tropical Moist Broadleaf40Africa Tropical Moist
Tropical Moist Broadleaf40Asia Tropical Moist
Temperate Broadleaf/Mixed50, 60Temperate Broadleaf
Temperate Conifer70, 90Temperate Conifer
Tropical Savanna/Shrub110, 120, 130Tropical Shrublands
Tropical Dry Broadleaf110, 120, 130Tropical Dry Broadleaf
Boreal + Tundra70, 90America Boreal
Boreal + Tundra70, 90Eurasia Boreal
Tropical Moist Broadleaf160Swamp Forest/Fresh Water
Tropical Moist Broadleaf170Mangrove/Saline Water
* Please refer to Table S1 for a list of GlobCover class names corresponding to the class numbers shown here.
Table
Table 2. Empirically fitted coefficients for correlation between ALOS HV sigma-0 and AGB for various forest types across the globe. The equation follows the form given in Equation (2). Method of determining forest categories is listed in Table 1.
Table 2. Empirically fitted coefficients for correlation between ALOS HV sigma-0 and AGB for various forest types across the globe. The equation follows the form given in Equation (2). Method of determining forest categories is listed in Table 1.
CategoryABCα
Africa Tropical Moist0.0564920.06468900.038247
Asia Tropical Moist0.0454090.06051800.060518
America Tropical Moist0.0405460.06878400.098841
Temperate Conifer0.00925650.0573360.040.27162
Temperate Broadleaf/Mixed0.0414690.0342960.0264060.012282
Tropical Shrubland0.0164290.1101300.2675
Tropical Dry Broadleaf0.0215630.0423240.0275190.1117
North America Boreal0.0189110.0197440.0291060.15723
Eurasia Boreal0.00916050.0385060.040.26141
Fresh Water Flooded0.0478450.0455810.0221640.0058592
Saline Water flooded0.0136820.0518460.021920.21116

Share and Cite

MDPI and ACS Style

Yu, Y.; Saatchi, S. Sensitivity of L-Band SAR Backscatter to Aboveground Biomass of Global Forests. Remote Sens. 2016, 8, 522. https://doi.org/10.3390/rs8060522

AMA Style

Yu Y, Saatchi S. Sensitivity of L-Band SAR Backscatter to Aboveground Biomass of Global Forests. Remote Sensing. 2016; 8(6):522. https://doi.org/10.3390/rs8060522

Chicago/Turabian Style

Yu, Yifan, and Sassan Saatchi. 2016. "Sensitivity of L-Band SAR Backscatter to Aboveground Biomass of Global Forests" Remote Sensing 8, no. 6: 522. https://doi.org/10.3390/rs8060522

APA Style

Yu, Y., & Saatchi, S. (2016). Sensitivity of L-Band SAR Backscatter to Aboveground Biomass of Global Forests. Remote Sensing, 8(6), 522. https://doi.org/10.3390/rs8060522

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop