A Scale-Driven Change Detection Method Incorporating Uncertainty Analysis for Remote Sensing Images

Abstract

Change detection (CD) based on remote sensing images plays an important role in Earth observation. However, the CD accuracy is usually affected by sunlight and atmospheric conditions and sensor calibration. In this study, a scale-driven CD method incorporating uncertainty analysis is proposed to increase CD accuracy. First, two temporal images are stacked and segmented into multiscale segmentation maps. Then, a pixel-based change map with memberships belonging to changed and unchanged parts is obtained by fuzzy c-means clustering. Finally, based on the Dempster-Shafer evidence theory, the proposed scale-driven CD method incorporating uncertainty analysis is performed on the multiscale segmentation maps and the pixel-based change map. Two experiments were carried out on Landsat-7 Enhanced Thematic Mapper Plus (ETM+) and SPOT 5 data sets. The ratio of total errors can be reduced to 4.0% and 7.5% for the ETM+ and SPOT 5 data sets in this study, respectively. Moreover, the proposed approach outperforms some state-of-the-art CD methods and provides an effective solution for CD.

1. Introduction

Change detection (CD) is a technique to detect changes occurred on the Earth. It is usually performed by analyzing remotely sensed images acquired from the same geographical area at different times [1,2]. This technique has been used widely in many practical applications due to its cost-effective characteristic, increasing temporal and spatial resolution, such as disaster detection [3], urban growth [4], and more general land cover/land use CD [5].

Considering the differences between multitemporal images (e.g., sunlight and atmospheric conditions, sensor differences, spectral characteristics, and registration strategy), image pre-processing techniques (such as atmospheric correction, image registration, geometric and topographic corrections) are necessary. A number of CD methods [3,6,7] have been investigated to reduce uncertainties in CD. Generally, these methods can be divided into post-classification (supervised) and comparative (unsupervised) methods. The former separately classifies the multitemporal images and finds changes by comparing individual-date classification maps. The post-classification methods have the advantages of providing ‘from-to’ change information and minimizing the impact of sensor and environmental differences. However, this type of method requires an analyst to acquire classification maps and the accuracy of the change maps depends on the quality of all individual-date maps [8,9]. With respect to the comparative approach, it detects changes by directly comparing the differences between multitemporal images based on spectral and texture characteristics. In this study, we focus on unsupervised CD.

The visual analysis was one of the earliest technologies for detecting changes, such as coastal areas [10], forest changes [11], and changes of the Broads Environmentally Sensitive Area [12]. The comparative methods were also developed, including image differencing, image ratio, image regression, principal component analysis and change vector analysis (CVA). They are generally pixel-based methods. Such methods have been used widely because of their easy implementation and direct reflection of changes. Some manual and empirical methods were exploited to determine a threshold involved in the comparative methods [13]. Furthermore, some automated threshold determination techniques were proposed by minimizing the measures of fuzziness [14], minimizing the least error probability based on Bayesian theory [15], and histogram-based methods [16]. Generally, changes are presented as a region that is large to be detected by the sensor used. A pixel belonging to changed or unchanged classes is likely to be surrounded by pixels belonging to the same class. Therefore, more reliable and accurate CD results can be yielded by properly using spatial information. A large number of pattern recognition methods incorporating spatial information were developed to reduce noise, such as fuzzy c-means (FCM) clustering [17,18], genetic algorithm [19,20], active contour model [21,22], and Markov random field [7,23]. These methods have their advantages in not requiring a threshold and in removing noise. Due to the uncertain overlap between the changed and unchanged pixels in the difference image, however, they have limitations in separating changed and unchanged pixels [24].

With the development of satellite technology, increasing higher-resolution images are available for CD, where more details of spatial structure and lower spectral resolution can increase the uncertainty in CD. To cope with the uncertainty, object-based methods were proposed, in which high-resolution images are segmented into objects with homogenous region and changes are then detected in units of objects [25]. Generally, four kinds of object-based methods can be identified, namely image-object, class-object, multitemporal-object and hybrid methods [26]. The image-object methods are similar to pixel-based methods and directly compare image objects to detect changes based on objects’ spectral information or texture features [27,28]. The class-object methods detect ‘from-to’ changes by comparing classified objects from multitemporal images [29,30]. For multitemporal-object methods, the temporally sequential images are combined and then segmented together to produce changed objects [31]. The hybrid methods detect changes through both pixel- and object-based methods, where the image differencing is usually used to generate the difference image and the object-based analysis method is then implemented to detect changes [32]. The hybrid algorithm has shown advantages in reducing noisy changes by combining pixel- and object-based methods [33], but it remains unclear how the final change results are influenced by the different combinations of pixel- and object-based schemes due to the several steps involved [26].

The ranges of pixel values of the difference image belonging to the changed and unchanged parts generally have overlap in pixel-based schemes. In object-based schemes, the segmentation is a pivotal step to generate corresponding objects between images and surface of the earth. However, segmented objects from different image often vary geometrically due to some factors including illumination conditions, view angles and meteorological conditions [34]. Additionally, the segmentation process sometimes suffers from under-segmentation and over-segmentation errors, which may create objects that do not accurately represent real-world feature [35]. Thus, uncertainty in the object-based methods exists inevitably.

In this paper, a scale-driven CD method incorporating uncertainty analysis is proposed, where the pixel- and object-based schemes are combined to reduce the uncertainty and increase accuracy. The proposed method consists of three main steps as shown in Figure 1, namely multitemporal-object segmentation, FCM clustering and uncertainty analysis. First, two temporal images X₁ and X₂ both including L bands are stacked and segmented to generate multiscale segmentation maps. Then, FCM clusters the difference image obtained by CVA into an initial pixel-based change map, with pixels’ membership belonging to changed and unchanged parts. Third, the Dempster-Shafer (DS) evidence theory is used to analyze the uncertainty in the combination of pixel- and object-based schemes. Two experiments on Landsat-7 Enhanced Thematic Mapper Plus (ETM+) and SPOT 5 data sets were carried out to evaluate the proposed method.

2. Methodology

Two images ${\mathbf{X}}_1=\left\{X_{1l}(i,j)|1\le i\le m,1\le j\le n,1\le l\le L\right\}$ and ${\mathbf{X}}_2=\left\{X_{2l}(i,j)|1\le i\le m,1\le j\le n,1\le l\le L\right\}$ of size m × n and L bands were acquired by the same sensor from the same geographical area at two different times t₁ and t₂. The images were co-registered and radiometrically corrected beforehand. The main steps are presented below.

2.1. Multiscale Segmentation of Difference Image

Due to impacts of sunlight, atmospheric condition and phenology cycle, it is difficult to obtain exactly corresponding objects by segmenting two temporal images individually. It discourages the comparison of objects, as uncertainties are accumulated when generating one-to-one correspondence. Therefore, two temporal images X₁ and X₂ are stacked into one image $\mathbf{X}=\left\{X_l(i,j)|1\le i\le m,1\le j\le n,1\le l\le 2L\right\}$ by simple band stacking, and segmentation is implemented on the stacked image.

Many clustering methods have been investigated to segment images, such as k-means and iterative self-organizing data analysis techniques algorithm. The results depend on the initialization to a certain extent. Recently, statistical region merging (SRM) was proposed to segment images, which has the ability of removing significant noise, handling occlusions, and can perform scale-sensitive segmentations fast [36]. Thus, SRM is adopted to segment the stacked image in this study.

The stacked image X contains m × n pixels, with each pixel containing 2L values, each of the 2L channels belonging to the set {0, 1, …, g}, and g = 255 here. Let X* denote the perfect segment scene of observed image X. Each channel of X is obtained by sampling each statistical pixel of X* from a set of exactly Q independent random variables (taking values within [0, g/Q]) for observed 2L channels. The tuning Q controls the scale of segmentation: the larger it is, the more regions exist in the final segmentation.

The SRM segments an image based on an interaction between a merging predicate and an order in merging. The merging predicate $P\left(R,R^{\prime }\right)$ can be expressed as follows

$$P\left(R,R^{\prime }\right)=\{\begin{array}{ll}\text{true}& \text{if} \forall a\in \left[1,2,\dots ,2L\right],\left|{\overline{R^{\prime }}}_a-{\overline{R}}_a\right|\le b\left(R,R^{\prime }\right)\\ \text{false}& otherwise\end{array}$$

(1)

where R and $R^{\prime }$ denote a fixed couple of regions of X, ${\overline{R}}_a$ and ${\overline{R^{\prime }}}_a$ are the average grey values for channel a in region R and $R^{\prime }$, respectively, and $b\left(R,R^{\prime }\right)=g\sqrt{\frac{1}{2Q}\left(\frac{1}{\left|R\right|}+\frac{1}{\left|R^{\prime }\right|}\right)\text{ln}\frac{2}{\delta }}$ ($0<\delta <1$). If $P\left(R,R^{\prime }\right)=\text{true}$, R and $R^{\prime }$ are merged. The function f of merging order used to sort pixel pairs in X is described as

$$f_a\left(p,p^{\prime }\right)=\left|p_a-{p^{\prime }}_a\right|$$

(2)

where $p$ and $p^{\prime }$ are pixels in X, and $p_a$ and ${p^{\prime }}_a$ are the pixel grey values of channel a. The SRM is then performed to segment the stacked image with different Q values and multiscale segmentation maps are obtained.

2.2. Pixel-Based CD Using FCM

In this part, CVA is used to generate the difference image, and FCM clusters the difference image to produce a change map with memberships belonging to changed and unchanged parts. First, the change vector $\Delta \mathbf{X}$ can be calculated as follows

$$\Delta \mathbf{X}(i,j)={\mathbf{X}}_1(i,j)-{\mathbf{X}}_2(i,j)=\left(\begin{array}{c}{x}_{11}(i,j)-x_{21}(i,j)\\ x_{12}(i,j)-x_{22}(i,j)\\ \cdots \\ x_{1L}(i,j)-x_{2L}(i,j)\end{array}\right)$$

(3)

where $\Delta \mathbf{X}$ includes all the spectral change information between X₁ and X₂ for a given pixel. The modulus $\Vert \Delta \mathbf{X}\Vert$ of change vector $\Delta \mathbf{X}$ is computed using Equation (4), which is recorded as the final difference image X_d.

$${\mathbf{X}}_{\mathrm{d}}(i,j)=\Vert \Delta \mathbf{X}(i,j)\Vert =\sqrt{{\displaystyle \sum _{b=1}^L(x_{1b}(}i,j)-x_{2b}(i,j){)}^2}$$

(4)

The difference image X_d is then normalized to [0, 255] in order to avoid the instability and inconsistency among the data sets and supply a consistent input for the following FCM clustering.

Afterwards, FCM [37] is implemented to cluster the difference image and detect changes. The membership probability $u_{ij}\in [0,1]$ (${\displaystyle \sum _{i=1}^c{u}_{ij}=1(j=1,2,\dots ,n)}$, c is the cluster number), that is, the pixel x_j in the difference image belonging to the i-th (i = 1 or 2) cluster, is determined by minimizing the objective function

$$J(\mathbf{U},\mathbf{V})={\displaystyle \sum _{i=1}^c{\displaystyle \sum _{j=1}^n{u}_{ij}^m{\Vert x_j-v_i\Vert }^2}}$$

(5)

where U = [u_ij] is the membership probability matrix of X_d, and V = [v₁, v₂, …, v_c] is the matrix composed of c central values. The membership probability u_ij can be calculated using the following equation

$$u_{ij}=\frac{1}{{\displaystyle \sum _{k=1}^c{\left(\frac{\Vert x_j-v_i\Vert }{\Vert x_j-v_k\Vert }\right)}^{\frac{2}{m-1}}}}$$

(6)

In Equation (6), v_i is computed as follows

$$v_i=\frac{{\displaystyle \sum _{j=1}^n{u}_{ij}^m{x}_j}}{{\displaystyle \sum _{j=1}^n{u}_{ij}^m}}$$

(7)

where m is a weighting exponent. For most data, 1.5 ≤ m ≤ 3 leads to satisfactory results [37]. It is set to 2 in this study, a widely used choice in many works [7,38].

An optimum solution can be obtained by updating U and V iteratively, and the iteration process is stopped when the number of iterations reaches a predefined maximum number or $\Vert {\mathbf{V}}_t-{\mathbf{V}}_{t-1}\Vert <\epsilon$ is achieved, where V_t and V_t−1 are the cluster center matrix in the t-th and (t−1)-th iteration and $\epsilon$ is a predefined threshold. Finally, an initial change map and the membership probability U of pixels in the difference image are produced and used for uncertainty analysis.

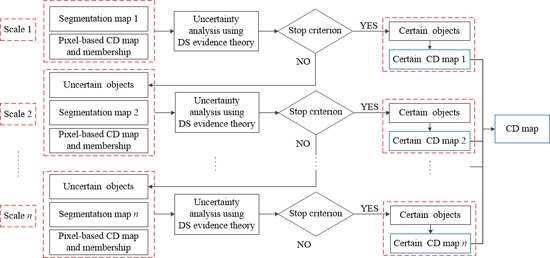
2.3. Scale-Driven CD Incorporating Uncertainty Analysis (SDCDUA)

In this study, a scale-driven solution is proposed to analyze the uncertainty existing in traditional CD, where DS evidence theory is employed, as shown in Figure 2.

First, a coarse segmentation map of SRM is analyzed based on the pixel-based CD map and memberships. Then, it is classified into changed, unchanged, and uncertain parts through the uncertainty analysis using the DS evidence theory. More details of the DS evidence theory are introduced in the following content. Only certain changed and unchanged objects are included in ‘Certain CD map 1’ shown in Figure 2. Second, for uncertain objects after the uncertain analysis, the next scale segmentation map with more detailed objects is adopted and analyzed with the pixel-based CD map and memberships. In this stage, the uncertain objects are also divided into changed, unchanged and uncertain parts, and a CD map consisting of identified changed and unchanged objects is also obtained, labeled as ‘Certain CD map 2’ in Figure 2. Next, the uncertain parts are further analyzed as showed in the last stage, which iterates until no uncertain object exits or the final segmentation map has been utilized. Finally, all ‘Certain CD maps’ are combined together to generate the final CD map.

The main step of uncertainty analysis based on DS evidence theory in SDCDUA is presented as follows. The DS evidence theory is an extension of the traditional Bayesian theory. The theory was first introduced by Dempster [39] in the context of statistical inference, and it was later extended to a general framework for modeling epistemic uncertainty by Shafer [40]. Three important functions in DS theory are defined and used to model the uncertainty, namely, the basic probability assignment function (m), the Belief function (Bel), and the Plausibility function (Pls).

Let $\Theta$ be the space of hypothesis and $2^{\Theta }$ denote the set of subsets of $\Theta$. For any hypothesis A of $2^{\Theta }$, m(A) ∈ [0, 1] and

$$\{\begin{array}{l}m(\mathrm{\varnothing })=0\\ {\displaystyle \sum _{A\subset 2^{\Theta }}m}(A)=1\end{array}$$

(8)

where ∅ represents the null set, m is the basic probability assignment function (BPAF), and m(A) denotes the basic probability of the hypothesis A.

Generally, the belief degree of the combined result from different evidences is represented with an interval. The upper and lower limits of the interval are called the Belief function (Bel) and the Plausibility function (Pls), respectively, which are computed as follows

$$\begin{array}{l}\{\begin{array}{l}Bel(A)={\displaystyle \sum _{B\subset A}m}(B)\\ Pls(A)={\displaystyle \sum _{B\cap A\ne \mathrm{\varnothing }}m(B)}\end{array}\end{array}$$

(9)

where A and B are made up of several or all the elements in $\Theta$, $B\subset A$, and the values of Bel and Pls range from [0, 1].

A new evidence m(c) is then calculated by fusing different source evidences using the following equation

$$\begin{array}{ll}m(F)& =m_1\oplus m_2\oplus \cdots \oplus m_n(F)\\ & =\frac{1}{k}{\displaystyle \sum _{X_1\cap \dots \cap X_{\mathrm{n}}=F}{\displaystyle \prod _{i=1}^n{m}_i}}(X_i)\end{array}$$

(10)

$$k={\displaystyle \sum _{X_1\cap \dots \cap X_{\mathrm{n}}\ne \mathrm{\varnothing }}{\displaystyle \prod _{i=1}^n{m}_i}}(X_i)$$

(11)

where $\oplus$ denotes the fusion of evidences, and m₁, m₂, …, m_n are the basis probability assignment function.

In CD problem, $\Theta =(C,U)$, where C denotes “change” and U represents “no-change”. Two evidences are generated and combined in this study. One is the object-based evidence $m_1$ produced based on the segmentation maps, and the other is the pixel-based evidence $m_2$ obtained with FCM. First, objects in a segmentation map are partitioned into changed and unchanged parts by minimizing the difference of grey values of pixels in each part, and the mean values of changed and unchanged parts are calculated. For an object R_i, its variances corresponding to changed and unchanged parts are obtained and termed $v_c^i$ and $v_u^i$, respectively. Thus, the evidence $m_1=\left\{P_{1\mathrm{c}},P_{1\mathrm{u}}\right\}$ of the object R_i can be obtained with the following equation

$$\{\begin{array}{l}{P}_{1\mathrm{c}}=v_u^i/(v_c^i+v_u^i)\\ P_{1\mathrm{u}}=v_c^i/(v_c^i+v_u^i)\end{array}$$

(12)

where $P_{1\mathrm{c}}$ and $P_{1\mathrm{u}}$ are probabilities of the object R_i belonging to changed and unchanged parts in the first evidence, respectively.

The second evidence $m_2=\left\{P_{2\mathrm{c}},P_{2\mathrm{u}}\right\}$ of the object R_i is calculated from the membership of pixels belonging to changed and unchanged parts with the following equation

$$\{\begin{array}{l}{P}_{2\mathrm{c}}={\displaystyle \sum _{j=1}^n{p}_{\mathrm{c}}^j}/n\\ P_{2\mathrm{u}}={\displaystyle \sum _{j=1}^n{p}_{\mathrm{u}}^j}/n\end{array}$$

(13)

where $P_{2\mathrm{c}}$ and $P_{2\mathrm{u}}$ are probabilities of the object R_i belonging to changed and unchanged parts in the second evidence, respectively, and n is the total number of pixels in the object R_i. $p_{\mathrm{c}}^j$ and $p_{\mathrm{u}}^j$ are probabilities of the j-th pixel belonging to changed and unchanged parts in the object R_i, respectively. They are computed by clustering the difference image using FCM algorithm in Section 2.2.

The evidences $m_1$ and $m_2$ are then combined into a new evidence $m=\{P_{\mathrm{c}},P_{\mathrm{u}}\}$, where $P_{\mathrm{c}}$ and $P_{\mathrm{u}}$ are probabilities of the object R_i belonging to changed and unchanged parts in the new evidence, respectively. For example, $m_1=\left\{P_{1\mathrm{c}}=0.6,P_{1\mathrm{u}}=0.4\right\}$ and $m_2=\left\{P_{2\mathrm{c}}=0.7,P_{2\mathrm{u}}=0.3\right\}$. k can be calculated using Equation (11) as

$$\begin{array}{ll}k& =m_1(\text{change})\cdot m_2(\text{change})+m_1\left(\text{no-change}\right)\cdot m_2\left(\text{no-change}\right)\\ & =P_{1\mathrm{c}}\cdot P_{2\mathrm{c}}+P_{1\mathrm{u}}\cdot P_{2\mathrm{u}}=0.54\end{array}$$

(14)

The P_c of the new evidence is calculated as

$$\begin{array}{ll}{m}_1\oplus m_2(\text{change})& =1/k\cdot {\displaystyle \sum _{X_1\cap X_2=\left\{\text{change}\right\}}{m}_1(X_1)\cdot m_2(X_2)}\\ & =1/k\cdot m_1(\text{change})\cdot m_2(\text{change})\\ & =1/k\cdot P_{1\mathrm{c}}\cdot P_{2\mathrm{c}}=0.78\end{array}$$

(15)

The P_u of the new evidence is computed as

$$\begin{array}{ll}{m}_1\oplus m_2(\text{no-change})& =1/k\cdot {\displaystyle \sum _{X_1\cap X_2=\left\{\text{no-change}\right\}}{m}_1(X_1)\cdot m_2(X_2)}\\ & =1/k\cdot m_1(\text{no-change})\cdot m_2(\text{no-change})\\ & =1/k\cdot P_{1\mathrm{u}}\cdot P_{2\mathrm{u}}=0.22\end{array}$$

(16)

A threshold $T_{\mathrm{m}}$ is then set to classify the object into unchanged, uncertain and changed groups with the following equation

$$l_i=\{\begin{array}{ll}1& P_{\mathrm{c}}>T_{\mathrm{m}}\\ 2& P_{\mathrm{u}}>T_{\mathrm{m}}\\ 3& \text{else}\end{array}$$

(17)

where l_i = 1, 2, 3 denote that the object R_i belongs to changed, changed and uncertain groups, respectively.

After the uncertainty analysis using DS evidence theory based on multiscale segmentation maps and pixel-based CD, a final change map can be obtained. For quantitative assessment on CD results, several indices are adopted: (1) Missed detections N_m that indicate the number of incorrectly classified unchanged pixels in the CD map. The ratio of missed detections P_m is calculated by $P_{\mathrm{m}}=N_{\mathrm{m}}/N_0\times 100\%$, where N₀ is the total number of changed pixels counted in the ground reference map; (2) False alarms N_f that indicate the number of the incorrectly classified changed pixels in the CD map. The ratio of false alarms P_f is calculated with the ratio $P_{\mathrm{f}}=N_{\mathrm{f}}/N_1\times 100\%$, where N₁ is the total number of unchanged pixels counted in the ground reference map; (3) Total errors N_t that indicate the total number of detection errors, including both missed and false detections. This total number refers to the sum of missed detections and false alarms. Hence, the ratio of total errors P_t is calculated with $P_{\mathrm{t}}=(N_{\mathrm{m}}+N_{\mathrm{f}})/(N_0+N_1)\times 100\%$.

3. Experimental Results and Analysis

Two experiments were conducted to test the performance of the proposed method, and each experiment includes two parts. In the first part, the effects of the initial segmentation map and threshold T_m were analyzed. In the second part, comparative experiments were carried out with some other effective CD methods, including distance regularized level set evolution (DRLSE) [41], CV model, multiresolution level set with Kittler algorithm (MLSK) [21] and expectation-maximization-based level set (EMLS) [22]. DRLSE is an enhanced level set method without revitalization of level set to detect objects. CV model detects changes by the evolution of a contour and minimizing the difference energy inside and outside the contour simultaneously. In MLSK, an initial change map is yielded as the initial contour, and level set is then implemented from coarse to fine difference images. The final change map is obtained from the fine resolution image. EMLS develops the level set method by adding more energy functions of changed and unchanged mean values from EM algorithm.

3.1. Experiments of Landsat-7 ETM+ Data Set

3.1.1. Description of Data Set 1

The first data set was acquired by the sensor of Landsat-7 ETM+ in August 2001 and August 2002 in the northeast of China. A section (400 × 400 pixels) of the entire scene was selected as the test site. Figure 3a,b show the true color images of 2001 and 2002, respectively. The image of 2001 was registered to image of 2002, and the histogram matching method was then implemented on both images for the relative radiometric correction. The difference image was then produced from six bands (except the thermal infrared channel) by CVA, as presented in Figure 3c. Figure 3d shows the reference map, which was obtained manually by a meticulous visual interpretation of the two temporal images. The changes were mainly caused by new crop planting.

3.1.2. Results and Analysis of Experiment 1

Several experiments were conducted according to the following: (1) an analysis of the effect of segmentation scale by implementing traditional object-based CD (OBCD); (2) a quantitative analysis of the performance of the proposed uncertainty analysis techniques in relation to different thresholds; and (3) comparisons among CD results obtained by the proposed method and some state-of-the-art CD methods.

In traditional object-based CD, objects are obtained from the segmentation maps and partitioned into changed and unchanged parts by minimizing the gray variance of objects in each group. Figure 4 shows CD maps generated from multiscale segmentation maps. It can be seen that only obvious changes or large-size changes are detected when a small Q is used, because a coarse segmentation map is produced. With the increase of Q, a more detailed segmentation map is obtained and a CD map including more detailed changes is generated as a result, as shown in Figure 4b,c. However, when Q reaches 256, some detailed changes are missed because of over segmentation.

Table 1. Accuracy of object-based CD results produced from different segmentation maps.

Q	Missed Detections		False Alarms		Total Errors
	Nm	Pm (%)	Nf	Pf (%)	Nt	Pt (%)
32	13,187	43.5	397	0.3	13,584	8.5
64	9357	30.9	869	0.7	10,226	6.4
128	10,580	34.9	815	0.6	11,395	7.1
256	12,457	41.1	566	0.4	13,023	8.1

presents the accuracy of CD results produced from different scale segmentation maps. The Q value of 64 gives the most accurate CD map among these results, where the ratio of total errors is 6.4%. The reason is that the Q value of 64 leads to a more satisfying segmentation map.

Figure 5 presents the results of uncertainty analysis based on the first scale segmentation map and pixel-based CD result from FCM, where black, white and gray represent unchanged, changed and uncertain parts, respectively. The first scale segmentation map used in SDCDUA is generated with Q = 64. The value of the threshold T_m ranges from 0.6 to 0.9 with steps 0.5, producing results in Figure 5a–g. As can be seen, few uncertain regions exist in the initial CD map when the threshold ranges from 0.6 to 0.75, and more regions are identified as uncertain parts with the increase of threshold. The DS theory is used to fuse the object-based results and pixels’ memberships to analyze the uncertainty in CD.

Figure 6 shows final CD results when the threshold ranges from 0.6 to 0.9 with steps 0.5. It is obvious that similar CD maps are obtained for different thresholds.

Table 2. Accuracy of CD results for different thresholds of data set 1.

Tm	Missed Detections		False Alarms		Total Errors
	Nm	Pm (%)	Nf	Pf (%)	Nt	Pt (%)
0.6	4896	16.2	1735	1.3	6631	4.2
0.65	4632	15.3	1779	1.4	6411	4.0
0.7	4632	15.3	1779	1.4	6411	4.0
0.75	4632	15.3	1779	1.4	6411	4.0
0.8	4653	15.4	1774	1.4	6427	4.0
0.85	4653	15.4	1774	1.4	6427	4.0
0.9	4896	16.2	1774	1.4	6670	4.2

describes the accuracy of different CD maps, where results having the same total errors of around 4.0% are produced as the threshold ranges from 0.6 to 0.9.

To evaluate the effectiveness of the proposed approach, some state-of-the-art methods are used as benchmarks, such as DRLSE, CV, MLSK, and EMAC. Figure 7 shows CD maps obtained by different methods. There is a parameter μ tuning the tradeoff between the fitness and the length of the contour in CV, MLSK and EMAC. With the increase of μ, more false alarms can be removed but over-smooth results are obtained. In this study, μ was set to 0.1 for CV, MLSK and EMAC. It is obvious that many false alarms are detected by DRLSE, MLSK and EMAC, and some missed detections exist in DRLSE and MLSK results. The CD map generated by CV contains more false alarms than the other methods, as shown in Figure 7b. Though OBCD removes many false alarms than the above-mentioned four methods (i.e., DRLSE, CV, MLSK and EMAC), a number of missed detections are produced. Figure 7f shows the CD map obtained by the proposed method, where the threshold was set to 0.85. It is worth noting that the proposed method generates the closest change map to the reference map.

Table 3. Quantitative comparison between the comparative and proposed methods for data set 1.

Methods	Missed Detections		False Alarms		Total Errors
	Nm	Pm (%)	Nf	Pf (%)	Nt	Pt (%)
DRLSE	9149	30.2	4021	3.1	13,440	8.4
CV	6302	20.8	9858	7.6	16,160	10.1
MLSK	7483	24.7	5059	3.9	12,542	7.8
EMAC	7604	25.1	4151	3.2	11,755	7.3
OBCD	9357	30.9	869	0.7	10,226	6.4
SDCDUA	4653	15.4	1774	1.4	6427	4.0

displays the quantitative comparisons between the comparative and proposed methods for data set 1. It can be found that OBCD generates a more accurate CD map than the pixel-based methods. The proposed method produces the change map with total errors of 4.0%, which decrease the total errors by 2.4% and at least 3.3% in comparison with the traditional object-based method and pixel-based methods, respectively.

3.2. Experiments of SPOT 5 Data Set

3.2.1. Description of Data Set 2

The second data set, which included two high-resolution images acquired from the same geographical area of Tianjin City, China, was used to evaluate the proposed method. The two images were acquired by SPOT 5 in April 2008 and February 2009, and were generated by fusing the panchromatic with three multispectral images. An area with 346 × 434 pixels was cropped from the entire images as the test site. The image of 2008 was registered to the image of 2009, and a histogram-matching method was implemented on both images for the relative radiometric correction. The difference image was generated with CVA, as shown in Figure 8c. Figure 8d shows the reference image obtained manually by a meticulous visual interpretation of the two temporal images, where changes occurred mainly due to new buildings.

3.2.2. Results and Analysis of Experiment 2

Figure 9 shows CD maps produced by the traditional object-based method with different segmentation scales. As can be seen from Figure 9, only main changes are detected from a coarse segmentation map generated using a small Q. With the increase of Q, more detailed segmentation maps are obtained, and more satisfying results are produced for values of 64 and 128. Many changes are lost for Q = 256 because of the over segmentation.

Table 4. Accuracy of object-based CD results for different scale segmentation maps.

Q	Missed Detections		False Alarms		Total Errors
	Nm	Pm (%)	Nf	Pf (%)	Nt	Pt (%)
32	23,929	68.0	1705	0.8	25,634	10.6
64	15,503	44.1	7362	3.5	22,865	9.4
128	13,552	38.5	10,941	5.3	24,493	10.1
256	30,054	85.4	1487	0.7	31,541	13.0

lists the accuracy of CD maps produced from different scale segmentation maps. The CD map generated by the Q value of 64 represents the most accurate one, where the ratio of total errors is 9.4%.

Figure 10 shows the results of uncertainty analysis for the first scale segmentation map using the SDCDUA method, where black, white and gray represent unchanged, changed and uncertain parts. The segmentation map is generated for a Q value of 64, and the threshold T_m ranges from 0.6 to 0.9 with steps 0.5. The corresponding results are shown in Figure 10a–g. It is seen that there are almost no uncertain regions when T_m equals 0.6, and very close uncertain regions are obtained when T_m ranges from 0.65 to 0.85. Many uncertain regions exist in the result produced for a threshold of 0.9.

Figure 11 shows the final CD maps of SDCDUA yielded with different thresholds, and

Table 5. Accuracy of CD results produced with different thresholds of data set 2.

Tm	Missed Detections		False Alarms		Total Errors
	Nm	Pm (%)	Nf	Pf (%)	Nt	Pt (%)
0.6	12,345	35.1	8046	3.9	20,391	8.4
0.65	12,345	35.1	8247	4.0	20,592	8.5
0.7	12,345	35.1	8247	4.0	20,592	8.5
0.75	12,345	35.1	8247	4.0	20,592	8.5
0.8	12,345	35.1	8247	4.0	20,592	8.5
0.85	12,345	35.1	8247	4.0	20,592	8.5
0.9	12,954	36.8	5339	2.6	18,293	7.5

is the corresponding accuracy. Similar CD maps are produced as the threshold ranges from 0.6 to 0.85, and ratio of total errors is 8.5%. The threshold of 0.9 leads to the most accurate CD map with a ratio of total errors of 7.5%.

The DRLSE, CV, MLSK and EMAC methods were implemented and compared with the proposed method. Figure 12 shows CD maps generated by different methods, where μ was set to 0.35 for CV and MLSK and 0.1 for EMAC, respectively. A number of false alarms exist in CD maps generated by DRLSE, CV, MLSK and EMAC due to the influence of building shadows and seasonal changes. Though OBCD removes many false alarms, many real changes are also removed at the same time. The proposed method detects most of the real changes and obtains a CD map closest to the reference map, as shown in Figure 12f.

Table 6. Quantitative comparison between the comparative and proposed methods for data set 2.

Methods	Missed Detections		False Alarms		Total Errors
	Nm	Pm (%)	Nf	Pf (%)	Nt	Pt (%)
DRLSE	17,700	50.3	7480	3.6	25,180	10.3
CV	9747	27.7	21,401	10.3	31,148	12.8
MLSK	12,035	34.2	16,830	8.1	28,913	11.9
EMAC	12,633	35.9	13,921	6.7	26,554	10.9
OBCD	15,503	44.1	7362	3.5	22,865	9.4
SDCDUA	12,954	36.8	5339	2.6	18,293	7.5

displays the quantitative comparison between the comparative and proposed methods. It can be found that the object-based methods generate more accurate CD maps than the pixel-based methods. The proposed method produces a CD map with the ratio of total errors of 7.5%, which decrease the ratio of total errors by 1.9% and at least 3.4% compared with the traditional object-based method and pixel-based methods, respectively. For high-resolution images, however, the accuracy increase by the proposed method is not obvious. A possible reason is that the difference image generated using only spectral features may be not sufficient due to the larger intra-spectral variation in high resolution images. This issue is exacerbated by pan-sharpening (as applied to the two images), a process that may enlarge the intra-spectral variation.

4. Discussion

This paper presents a CD approach that incorporates uncertainty analysis to reduce uncertainties in CD. The DS evidence theory is adopted to increase the accuracy of CD maps by fusing two evidences. One piece of evidence is designed based on the memberships of pixels obtained from FCM clustering pixels into changed and unchanged classes. The other is produced from the multiscale segmentation maps yielded by SRM. A scale-driven approach is proposed to account for pixel- and object-based information at the same time by fusing the two evidences. Two experiments were carried out on Landsat-7 ETM+ and SPOT 5 data sets and results show the efficiency of proposed approach. In summary, the proposed approach holds the following characteristics and advantages: (1) The proposed approach incorporates pixel- and object-based CD results. It introduces fuzzy information of all pixels based on gray values and considers contextual information, which inherits merits of the pixel- and object-based methods; (2) A scale-driven strategy is proposed to choose multiscale segmentation maps from coarse to fine scale in the uncertainty analysis, which solves the scale issue in segmentation and make the best use of contextual information; (sechon3) The uncertainty analysis technique is used in the scale-driven strategy to fuse evidences from pixel-based results and multiscale segmentation maps, which increases the accuracy and robustness of CD.

The proposed approach consists of three main steps, including multiscale segmentation of stacked temporal images, clustering of the difference image and uncertainty analysis. In the three different phases, SRM, FCM and DS evidence theory are used in this study. Other alternatives can also be considered. For example, the mean shift and MRF-based segmentation methods can be used to segment stacked images; fuzzy set, another uncertainty analysis methods, is expected to replace DS evidence theory to fuse pixel- and object-based information. In future research, it would be interesting to incorporate these potential alternatives into the framework presented in this study and have a systematic comparison between the derived solutions and the method proposed in this study.

In the proposed approach, two parameters Q and T_m are involved. From Table 1 and Table 4, we can see that the CD accuracy is the greatest when Q takes 64, as this value leads to the most satisfying segmentation map. For the threshold T_m, it can be seen from Table 2 and Table 5 that the CD accuracy of the proposed approach does not change much with its variation. Thus, we recommend that the parameter Q can be set to 64 and the threshold T_m can be selected within the interval of [0.8, 0.9].

In this study, as a first evaluation, the proposed approach was performed on bi-temporal images from the same sensor. Images acquired by different sensors usually have different characteristics (e.g., spectral resolution, spatial resolution and band number). Thus, multitemporal images cannot be stacked and segmented straightforwardly. In addition, traditional CD methods (e.g., image dereferencing and CVA) cannot be used directly to generate a difference image. The approach proposed in this study is designed as a framework for incorporating uncertainty analysis of pixel- and object-based methods. In future research, we will focus on developing effective multiscale segmentation and pixel-based CD methods to make the proposed approach suitable for multi-sensor and multitemporal image CD. Some literature [42,43] shows that temporal correlation exists between long-term time-series images. It can be potentially used to increase CD accuracy. It would be interesting to further extend the proposed approach for continuous CD based on multitemporal images, where temporal correlation exists between images. It is expected that the temporal information would help to further reduce the uncertainties in CD. This issue motivates future research.

5. Conclusions

In this paper, a scale-driven CD method incorporating uncertainty analysis is proposed, where the pixel- and object-based schemes are combined and analyzed together to increase CD accuracy. Two experiments were carried out on Landsat-7 ETM+ and SPOT 5 data sets, and using the proposed approach, the ratios of total errors are reduced to 4% and 7.5%, respectively. Compared with some popular pixel-based methods (i.e., DRLSE, CV, MLSK and EMAC), the ratios of total errors are reduced at least by 3.3% and 2.8%, respectively. The proposed method generates more accurate CD results than the benchmark methods tested in this study. Therefore, the proposed method provides an effective new solution for CD. Future research will be focused on extending the proposed SDCDUA to multi-sensor and multitemporal image CD.