1. Introduction
Conventional supervised classification algorithms (e.g., decision tree (DT) [
1], naive Bayesian (NB) [
2] and back propagation neural network (BPNN) [
3]) can provide satisfying classification performance and have been widely used in traditional data classification, such as web page classification [
4,
5], medical image classification [
6,
7] and face recognition [
8]. However, performance strongly depends on the quantity and quality of training samples. Labeled samples are often difficult, costly or time consuming to obtain, and they may not perform well on hyperspectral imagery due to the Hughes phenomenon when the number of training samples is limited [
9,
10]. Therefore, semi-supervised learning attempts to use unlabeled samples to improve classification [
11,
12,
13]. Common semi-supervised learning algorithms include multi-view learning [
14,
15], self-learning [
16,
17], co-training [
18,
19], graph-based approaches [
20,
21], transductive support vector machines (TSVM) [
22,
23], etc.
Semi-supervised learning has been of great interest to hyperspectral remote sensing image analysis. In [
24], semi-supervised probabilistic principal component analysis, semi-supervised local fisher discriminant analysis and semi-supervised dimensionality reduction with pairwise constraints were extended to extract features in a hyperspectral image. In [
25], a new classification methodology based on spatial-spectral label propagation was proposed. Dopido and Li developed a new framework for semi-supervised learning, which exploits active learning (AL) for unlabeled samples’ selection [
26]. In [
27], a new semi-supervised algorithm combined spatial neighborhood information in determining class labels of selected unlabeled samples. Tan proposed a semi-supervised SVM with a segmentation-based ensemble algorithm to use spatial information extracted by a segmentation algorithm for unlabeled samples’ selection in [
28].
Meanwhile, Blum and Mitchell proposed a prominent approach called co-training, which has become popular in semi-supervised learning [
19]. This algorithm requires two sufficient and redundant views, but this requirement cannot be met for hyperspectral imagery. Then, Gold and Zhou proposed a new co-training method called statistical co-training [
29], which employed two different learning algorithms based on a single view. In [
30], another new co-training method called democratic co-training was proposed. However, the aforementioned algorithms employ a time-consuming cross-validation technique to determine how to label the selected unlabeled samples and how to produce the final hypothesis. Therefore, Zhou and Li developed tri-training in [
31]. It neither requires the instance space to be described with sufficient and redundant views nor imposes any constraints on supervised learning algorithms, and its applicability is broader than previous co-training style algorithms. However, tri-training has some drawbacks in three aspects: (1) selecting a complementary classifier may be difficult; (2) unlabeled samples may have error labels that are added to the training set during semi-supervised learning; (3) the final classification map may be contaminated by salt and pepper noise. In this paper, a novel tri-training algorithm is proposed. We use three measures of diversity, i.e., the double-fault measure, the disagreement metric and the correlation coefficient, to determine the optimal classifier combination, then unlabeled samples are selected using an active learning (AL) method and consistent results of any two classifiers combined with a spatial neighborhood information extraction strategy to predict the labels of unlabeled samples. Moreover, a multi-scale homogeneity (MSH) method is utilized to refine the classification result.
The remainder of this paper is organized as follows.
Section 2 briefly introduces the standard tri-training algorithm, then describes the proposed approach.
Section 3 presents experiments on three real hyperspectral datasets with a comparative study. Finally,
Section 4 concludes the paper.
2. Methodology
2.1. Tri-Training
In the standard tri-training algorithm, three classifiers are initially trained by a dataset generated via bootstrap sampling from the original labeled data. Then, for any classifier, an unlabeled sample can be labeled as long as another two classifiers agree on the labeling of this sample. This training process will stop when the results of the three classifiers reach consistency. The final predication is produced with a variant of majority voting among all of the classifiers.
2.2. The Proposed Approach
2.2.1. Classifier Selection
The principle of classifier selection is that classifiers should be different from each other and their performance should be complementary; otherwise, the overall decision will not be better than each individual decision. Three measures of diversity are implemented to select three classifiers from SVM [
32,
33,
34], multinomial logistic regression (MLR) [
35,
36], KNN [
27,
37] and extreme learning machine (ELM) [
38,
39]. The three measures of diversity are the double-fault measure, the disagreement metric and the correlation coefficient [
40], which are described as below.
(1) The correlation coefficient ():
Let
be a labeled dataset, K be the number of classifiers,
be the classifier and
be the output of
. If
recognizes correctly
,
, otherwise,
.
where
is the number of samples
of
for which
and
(see
Table 1). With the increase of
, the diversity of classifiers becomes smaller.
(2) Disagreement metric (D):
The disagreement between classifier outputs (correct/wrong) can be measured as:
where
is the number of samples
of
for which
and
(see
Table 1). With the increase of
D, the diversity of classifiers becomes larger.
(3) Double-fault measure (DF):
The double-fault between classifier outputs (correct/wrong) can be measured as:
where
is the number of samples
of
for which
and
(see
Table 1). With the increase of
DF, the diversity of classifiers becomes larger.
2.2.2. Unlabeled Sample Selection
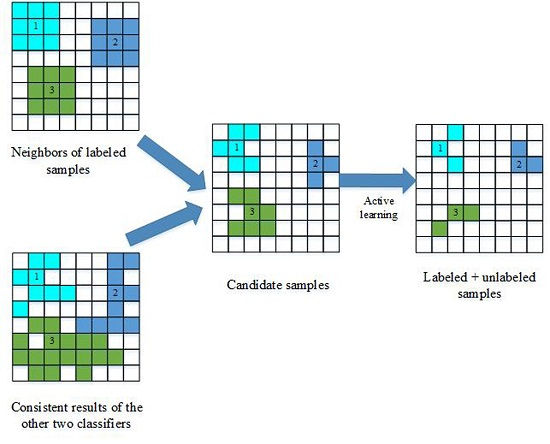
In the standard tri-training algorithm, for any classifier, an unlabeled sample can be labeled when another two classifiers agree on the labeling of this sample. However, the training set may be small; the label of unlabeled samples that two classifiers agree on may be wrong. Therefore, for any classifier, we use a spatial neighborhood information extraction strategy with an AL algorithm to select the most useful spatial neighbors as the new training set on the condition that two classifiers agree on the labeling of these samples.
Figure 1 illustrates how to select unlabeled samples, and the selection process includes two key steps, i.e., the construction of the candidate set and active learning.
(1) The construction of the candidate set:
For any classifier, we consider spatial neighborhood information with the consistent results of two classifiers to build the candidate set. Firstly, unlabeled samples are selected based on the consistency of two classifiers’ outputs, and those samples are considered reliable according to the standard tri-training algorithm. With a local similarity assumption, the neighbors of labeled training samples are identified using a second-order spatial connectivity, and the candidate set is built by analyzing the spectral similarity of these spatial neighbors. Since the output of a classifier is based on spectral information, the candidate set is obtained based on spectral and spatial information. Thus, these samples are more reliable.
(2) Active learning:
In semi-supervised learning, the main objective is to select the most useful and informative samples from the candidate set. However, some of the samples in the candidate set may not be useful for training the third classifier, because they may be too similar to the labeled samples. To prevent the introduction of such redundant information, the breaking ties (BT) [
17] algorithm is adopted to select the most informative samples.
The decision criterion of BT is:
where
is the most probable class for sample
,
is the probability when the label of sample
is
k and
K is the number of classes.
2.2.3. Multi-Scale Homogeneity Method
Some of the existing hyperspectral image classification algorithms produce classification results with salt and pepper noise. To solve this problem, we use the multi-scale homogeneity method. Let
be the initial classification result,
be the scale of a homogeneous region,
be the threshold of those homogeneous regions and
be the number of the samples that have the same label in a homogeneous region.
- (1)
An homogeneous region is built in the initial classification result. If , the samples in this region will have the same label; otherwise, the label of the samples does not change. Let this new result be the second classification result.
- (2)
A homogeneous region is built in the second classification result. If , the samples in this region will have the same label; otherwise, the label of the samples does not change. Let this new result be the third classification result.
- (3)
A homogeneous region is built in the third classification result. If , the samples in the homogeneity region will have the same label; otherwise, the label of the samples does not change. This new result will be the final classification result.
2.3. Semi-Supervised Classification Framework
Let be the initial training set, be the unlabeled set, be the classifiers and be the classification results.
The procedure of the proposed method is summarized as follows.
- (1)
Train the classifier with and obtain the predicted classification result ;
- (2)
For the classifier , select another two classifiers agreeing on the labeling of these samples to build the first candidate set;
- (3)
For , the neighbors of (using second-order spatial connectivity) will be labeled based on Tobler’s first law, and build the second candidate set;
- (4)
Conduct comparative analysis of the first and the second candidate set, and select these samples that have the same label to build the third candidate set;
- (5)
Use the BT method to select the most useful and information samples from the third candidate set, , ;
- (6)
Train the classifier with the new and obtain the predicted classification result ;
- (7)
Terminate if the final condition is met; otherwise, go to Step (2);
- (8)
Obtain that has the highest classification accuracy in these three classifiers and use the multi-scale homogeneity method to process to obtain the final classification result.
4. Discussion
In order to further assess the performance of the proposed method, we select some methods that combine semi-supervised spectral-spatial classification with active learning for comparison in this section. Reference results were provided in [
25] for the spatial-spectral label propagation based on the support vector machine (SS-LPSVM), the transductive SVM, MLR + AL proposed in [
25]. Additionally, the best reported accuracy from [
27] for the MLR + KNN + SNI (i.e., SNI is the spatial neighbor information) method and from [
43] for the semi-supervised classification algorithm based on spatial-spectral cluster (C-S2C) and the semi-supervised classification algorithm based on spectral cluster (SC-SC) is shown.
Table 8 and
Table 9 illustrate the classification overall accuracy of TT_AL_MSH_MKE in comparison with the above methods for the AVIRIS Indian Pines dataset and ROSIS Pavia University dataset. With the number of initial labeled samples increasing, the OA values of all methods are increased. When
L = 5, the best OA is obtained by TT_AL_MSH_MKE. For the AVIRIS Indian Pines dataset, the OA of TT_AL_MSH_MKE is 6.56% higher than MLR + KNN + SNI, respectively. For the ROSIS Pavia University dataset, the OA of TT_AL_MSH_MKE is 6.09%, 3.14% and 4.03% higher than MLR + KNN + SNI, respectively. The reason is that we select classifiers that are different from each other; their performances are complementary; and the classification performances are improved greatly, in particular for the small training datasets with 10 initial samples/class or less.
5. Conclusions
In this paper, a novel semi-supervised tri-training algorithm for hyperspectral image classification was proposed. In the proposed algorithm, three measures of diversity, i.e., double-fault measure, disagreement metric and correlation coefficient, are used to select the optimal classifier combination. Then, unlabeled samples were selected using the AL method and the consistent results of another two classifiers combined with spatial neighborhood information to predict the labels of unlabeled samples. Moreover, we utilize the multi-scale homogeneity method to refine the final classification result. To confirm the effectiveness of the proposed TT_AL_MSH_MKE, experiments were conducted on three real hyperspectral data, in comparison with the standard TT_MKE. Moreover, some methods that combine semi-supervised spectral-spatial classification with active learning are selected to validate the performance of the proposed method. Experiment results demonstrate that the OA of the proposed approaches is improved more than 10% compared with TT_MKE, and the proposed method outperforms other methods in particular for the small training datasets with 10 initial samples/class or less. Meanwhile, the proposed method can effectively reduce the salt and pepper noise in the classification maps.