1. Introduction
As the statistical character parameters describing the sea state, the wave height and period are important in theoretical research on ocean wave generation, developments in coastal and offshore engineering, and other applications. Traditionally, the significant wave height and the zero-crossing wave period are often obtained from sea wave frequency spectra measured by in situ buoys. However, the use of buoys is restricted to primarily coastal regions and, hence, cannot provide information on global ocean wave conditions.
The advent of synthetic aperture radar (SAR) and the space-borne satellite radar altimeter have changed this situation. Synthetic aperture radar is able to provide the two-dimensional surface wave spectra for longer waves and, hence, can only provide swell information [
1]. Alternatively, radar altimeters have the capability of estimating
and wind speed, in addition to the sea surface height. Moreover, subsequent studies have also indicated the possibility of retrieving
from
and the backscatter coefficient
, measurements of altimeters, and numerous empirical models have been proposed in the last two decades (e.g., [
2,
3,
4,
5,
6]). However, these models perform worse in low-wind conditions than in high-wind conditions. In a recent study, a two-piece altimeter wave period model [
6] was proposed which is divided according to
, or the wind speed. This model produces root mean square errors for the estimation of
of approximately 0.5 s and 0.9 s for high- and low-wind conditions, respectively.
Note, however, that the wave period determined by altimeters’ and measurements is referred to as the geometric mean wave period , and is defined differently from the zero-crossing wave period , which could cause a systematic discrepancy in the comparisons. Therefore, in the present study, the geometric mean wave period directly calculated from buoy wave spectra is compared with the geometric mean wave period calculated from altimeter measurements.
The remainder of the present study is organized as follows. The dataset used in the present study and the definitions of the wave periods are presented in
Section 2 and
Section 3, respectively. In
Section 4, the comparison of
and
reveals that
is larger than
, primarily because buoys missed high-frequency sea waves having wavelengths that are shorter than the characteristic dimension of the buoy. When a wavenumber spectral model is used to obtain the data for high-frequency sea waves, the compensated buoy wave period
is confirmed to agree well with
, as described in
Section 5. In
Section 6, the difference between
and
and the effects of high-frequency sea waves are further discussed. Finally, a brief summary is presented in
Section 7.
3. Rationale of the Retrieval of Altimeter Wave Period
A sea state is the condition of the ocean surface, considered as a stochastic field, that is characterized by statistics such as the wave height, period, and direction-independent wavenumber spectrum
or frequency spectrum
, where
is the frequency in Hz and
is the wavenumber. In the case of buoy measurements,
is determined through a time series of buoy motion, and all of the basic wave measurements are derived from
n-th wave spectral moments, which are defined as:
Based on the linear theory assumption, the basic wave height and period parameters are calculated as follows [
10]:
Significant wave height (
):
Average zero-crossing wave period (
):
Moreover, the crest period
is defined as follows:
A wave buoy, which is finite in size, is not able to follow waves having wavelengths shorter than the approximate diameter of the buoy, and the corresponding limiting frequency is called the cut-off frequency. In the present study, we use and to represent the lower and upper cut-off frequencies, respectively. For most of the NDBC buoys considered in the present study, is 0.02 Hz, since waves with periods longer than 50 s are practically negligible. Meanwhile, is 0.485 Hz, and thus, based on the deep water dispersion relationship, , data for high-frequency sea waves having wavelengths of less than approximately 6.6 m are not captured.
Unlike buoy measurements, radar altimeters cannot capture the spectral information of sea waves. Instead, and are directly derived from the one-second averaged time series of the sea surface echo of microwave radar (namely the waveform). We hereinafter use superscripts A and B to indicate altimeter and buoy measurements, respectively. For example, and represent significant wave height measurements obtained by an altimeter and a buoy, respectively.
For near-nadir incidence radar applications, the backscatter coefficient,
, is commonly considered as being due primarily to specular reflection and is inversely proportional to the wind stress. For an isotropic rough surface having a Gaussian distribution, the backscatter coefficient due to specular reflection can be expressed as follows [
11]:
where
is the backscatter coefficient in natural units,
is the Fresnel reflection coefficient at normal incidence characterizing the surface reflectivity,
is the filtered mean square slope (
MSS) of the sea surface measured by altimeter, and
is the radar incidence angle. In the present study, we use
[
12], and
represents the portion of surface roughness elements having length scales greater than the diffraction limit, 3
λ, where
λ is the radar wavelength [
13], namely greater than 6.6 cm for the 2.2 cm Ku-band radar altimeter. For normal incidence radar altimeters,
, Equation (5) can be simplified as follows:
The
MSS can be obtained by integrating the slope spectrum,
, as [
14]:
where
is the direction-independent wavenumber spectrum. Using the deep water dispersion relationship and the Jacobian operator as in [
15], the
MSS can be expressed using the direction-independent frequency spectrum,
, as follows [
16]:
where
is the fourth spectral moment, and g represents the acceleration of gravity.
Based on Equations (3) and (4), the geometric mean wave period
can be defined as follows [
1]:
For buoy measurements,
can be obtained directly from spectral moments by:
Based on Equations (2), (6), (8), and (9),
can be derived from altimeter measurements by:
Therefore, both altimeter and buoy measurements can be used to obtain
. Note that this formulation is very similar to that of [
3], which used heuristic arguments to show that the wave period can be retrieved using a linear relationship, namely
.
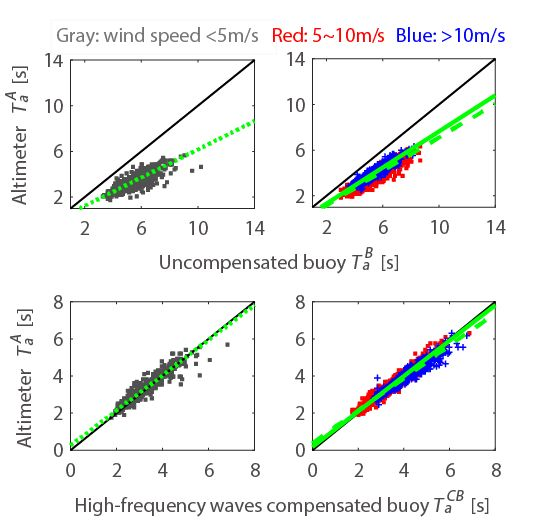
4. Comparison of Geometric Mean Wave Periods Determined from Buoy and Altimeter Data
In this paper, we use various statistics to quantify the comparisons, namely the correlation coefficient (CC), bias, slope of the regression line, and root mean square difference (RMSD) around the regression line. First, the wave periods
and
, which are defined differently, are compared, as shown in
Figure 2. Referring to the two-piece wave model proposed by [
6], the plots are divided according to the wind speed conditions. The geometric mean wave period determined by altimeter data
is positively correlated with the zero-crossing wave period determined by buoy data
under all wind conditions. However, as the wind speed decreases, the CC and RMSD around the regression line estimated by the orthogonal distance regression (ODR) method [
17] become small and large, respectively, as shown in
Table 1. In addition,
is always significantly shorter than
. This could be due to either the difference in the definitions of the wave periods or the observation methods, or even due to improper choice of the
constant.
Next, the geometric mean wave periods of the buoys
were directly calculated from wave spectra and were compared with
, as shown in
Figure 3. Compared with
Figure 2, the estimated wave periods
and
(defined similarly) result in better agreement than wave periods
and
(defined differently). In particular, the slope of the regression lines becomes closer to unity. Nevertheless, a mean bias of 1.6 s (
) and an RMSD of 0.5 s around the regression line remain (
Table 1).
In order to examine the reason for the remaining discrepancy between
and
,
and
MSS are examined because they are directly related to
and
, respectively, which are used in the derivation of
. Altimeters are known for their ability to estimate significant wave height, and this was confirmed by the comparison of the present study, even in low-wind conditions. As shown in
Figure 4, the data of altimeter
almost perfectly agrees with that of buoy
, as determined by Equation (2), where the CC is 0.98 and the RMSD is 0.2 m.
On the other hand, the altimeter
, which is inversely proportional to
, is significantly larger than
calculated from the fourth moment of the wave spectra, as shown in
Figure 5. When the wind speed is higher than 5 m·s
−1,
and
exhibit a rough linear relationship with the CC exceeding 0.80. In low-wind conditions, the variation range of
is more limited than that of
. In other words,
appears to miss some variations that are observed by the altimeters.
As described in
Section 3, the buoy cannot measure waves having wavelengths shorter than the characteristic dimension of the buoy. Such a wave would have a larger slope even though its wave height is small, because its horizontal scale is smaller. Therefore, the high-frequency sea waves not captured by the buoy would contribute significantly to the
MSS, as shown in
Figure 5, but would contribute less to significant wave height, as shown in
Figure 4. In order to confirm this, in the following section, we use a wavenumber spectral model to estimate the
MSS of the high-frequency sea waves missed by buoys, and the geometric mean wave period is estimated using the compensated buoy
MSS.
5. Compensation of the Mean Square Slope Obtained Using the Buoy Data
As discussed in
Section 3, the
MSS is theoretically defined by the direction-independent wavenumber spectrum
in Equation (7). Previous studies have shown that the universal form of the equilibrium range spectrum
is no longer rational and should be of the form
[
18,
19]. Although this form is supported by observations in the rear face region of the spectrum, it cannot be extended to very high wavenumbers. During the last two decades, numerous frequency domain observations have suggested that, in addition to the well-established
behavior in the rear face region, a fairly abrupt change in spectral slope occurs at approximately
, as compared to the slope that follows the
law [
20], where
is the peak wavenumber of wind waves, as defined by
, and
is the neutral wind speed at an elevation of 10 m.
Although the proper spectral form remains controversial, the
MSS of the high-frequency sea waves,
, is estimated as follows [
21]:
The first term on the right-hand side of Equation (12) represents the equilibrium range spectrum, and the second term indicates the saturation range spectrum, where
b = 5.2 × 10
−2,
is the wind friction velocity, g is the gravitational acceleration, and
B = 4.6 × 10
−2. The wavenumbers
and
reflect the integration limits of the low and high wavenumbers, respectively. Here,
and
are adopted to estimate the
MSS missing from the buoy measurements, corresponding to wavelengths approximately from 6 cm (or
of Ku-band radar) to 6.6 m (or the characteristic dimension of the buoy). The wavenumber
divides the wavenumber spectrum into the equilibrium range and the saturation range and is defined in [
21] as
where
is the drag coefficient for which we adopt the form proposed in [
22].
Figure 6 shows the wind speed dependency of
. As
(namely
) decreases with the increasing wind speed
, the first term on the right-hand side of Equation (12) decreases to zero when
becomes smaller than
, or when
exceeds approximately 10 m·s
−1.
After compensating for high-frequency sea waves, the compensated buoy mean square slope,
, shows no obvious bias with altimeter
(
Figure 7) compared with the uncompensated buoy mean square slope,
, even in low-wind conditions. The CC becomes 0.68 and 0.83 for wind speeds lower and higher than 5 m·s
−1, respectively.
The geometric mean wave period for the compensated buoy data,
, was calculated and compared with altimeter-derived
. As shown in
Figure 8,
is in better agreement with
than
(
Figure 3). The CC, mean bias (
), and RMSD are 0.97, less than 0.01 s, and 0.2 s, respectively, as listed in
Table 2.
Recall that the significant wave height
is not affected by the loss of high-frequency sea waves, as shown in
Figure 4. Since the higher-order moment forces more weight on high-frequency spectra in the integration, the contribution of high-frequency sea waves would become significant for
but negligible for
. This suggests that the
-based
would also be affected by the loss of high-frequency sea waves, but in a different manner from the
-based
. Therefore, in the following section, we examine the impact of missing high-frequency sea waves on
,
, and
.
6. Discussion
In order to increase the amount of data for comparison, all data from 30 NDBC buoys are used in this section to calculate
,
, and
, independently from the altimeter data. The data are divided into 16 subsets according to wind speed in intervals of 1 m·s
−1 (0–1 m·s
−1, 1–2 m·s
−1, …, 14–15 m·s
−1, and higher than 15 m·s
−1). As shown in
Figure 9, the data number of each subset exceeds 15,000 with a maximum of approximately 140,000 samples at 6 to 7 m·s
−1.
Figure 10 shows scatter plots of
with
or
for two wind conditions, together with the regression lines estimated by the ODR method. The slopes of the regression lines of
are closer to unity for both wind conditions. In other words, the discrepancy between
and
is much larger. Moreover, the RMSD around the regression line is much larger for
in the lower wind condition (
Figure 10a), whereas, for
, there is no significant difference between the two wind cases, which suggests that
is more sensitive to wind speed variation.
In order to examine the dependence of the relationship between
and
or
on wind speed, the slope and RMSD of the regression lines were calculated for each of the 16 data subsets, and the results are plotted in
Figure 11.
For
, the slope of the regression line varies only slightly with wind speed, and the RMSD remains small. In contrast, for
(also for
), the slope of the regression line varies with wind speed, especially in low-wind conditions. The presence of wind waves on background swells shortens
, resulting in the smaller slope of the regression lines. Since wind waves are more sensitive to wind speeds than swells, the growth of short wind waves decreases the slope values in
Figure 11a as the wind speed increases until the wind wave spectrum becomes saturated at winds stronger than 5 m·s
−1. On the other hand, neither
nor
includes short wind waves, and so they are independent of the growth of short wind waves. Therefore, the slope of
remains approximately constant, as shown in
Figure 11a.
In addition, because the growth of wind waves depends on not only wind speed but also wind duration, the mean wave periods would diverge even for the same instantaneous wind speed, especially for
, which is most sensitive to the growth of wind waves. This would result in a larger RMSD of
at a lower wind speed and is consistent with
Figure 11b.
7. Conclusions
In previous studies on altimeter wave period retrieval, great efforts were made to establish a relationship between the buoy-derived zero-crossing wave period with altimeter-measured significant wave height and the backscatter coefficient . However, all of the derived algorithms resulted in lower precision in low-wind conditions. Since radar altimeters only provide and information about the sea state, that is, the zeroth and fourth wave spectral moments, the geometric mean wave period, , is estimated from altimeter data and is different from the zero-crossing wave period, , which is commonly used by in situ buoys. In the present study, the geometric mean wave period derived from buoy wave spectra was directly compared with .
Higher-order wave spectral moments are more sensitive to high-frequency sea waves. A buoy cannot measure waves shorter than the characteristic dimension of the buoy, so that information of high-frequency sea waves is not captured. Since neither nor captures the contribution of high-frequency sea waves, they result in a near-linear relationship, independent of wind speed. On the other hand, (or the MSS) observed by altimeters has high sensitivity to high-frequency sea waves, so that is quite different from , especially in low-wind conditions.
When the MSS due to the missing high-frequency sea waves is compensated, the geometric mean wave period derived from buoy measurements, , agrees well with the altimeter-derived period, . This suggests that observed by altimeters is sufficiently accurate if proper in situ data are compared.
High sensitivity of the
MSS to high-frequency sea waves is not specific to the radar altimeter measurements, but rather is a common concern with respect to specular reflection. For example, global navigation satellite system reflectometry (GNSS-R) measurements also use the
MSS at the sea surface, and the retrieved GNSS-R
MSS was found to be larger than co-located buoy measurements due to the upper cut-off frequency of the buoy [
23]. Therefore, the loss of high-frequency waves by buoys should be carefully taken into consideration when buoy measurements are used to verify remote sensing measurements.