Evaluation of a Phenology-Dependent Response Method for Estimating Leaf Area Index of Rice Across Climate Gradients
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites
2.1.1. Haean, South Korea (HK)
2.1.2. Mase, Japan (MSE)
2.1.3. Shizukuish, Japan
2.1.4. Aso, Japan
2.1.5. El Saler-Sueca, Spain (ESES2)
2.2. Vegetation Index from Remote Sensing
2.3. Leaf Area Index Estimates
3. Results
3.1. Exponential Model for Estimating LAI
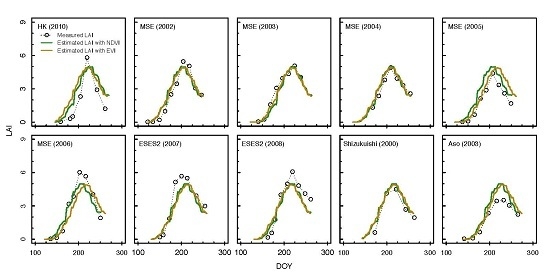
3.2. Estimation of LAI from the Consistent Development Curve Method
4. Discussion
4.1. Estimation of LAI using Different Growth Phases
4.2. Performance of the Consistent Development Curve Method
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bonan, G.B. Importance of leaf-area index and forest type when estimating photosynthesis in Boreal Forests. Remote Sens. Environ. 1993, 43, 303–314. [Google Scholar] [CrossRef]
- Chen, J.M.; Pavlic, G.; Brown, L.; Cihlar, J.; Leblanc, S.G.; White, H.P.; Hall, R.J.; Peddle, D.R.; King, D.J.; Trofymow, J.A.; et al. Derivation and validation of Canada-wide coarse-resolution leaf area index maps using high-resolution satellite imagery and ground measurements. Remote Sens. Environ. 2002, 80, 165–184. [Google Scholar] [CrossRef]
- Lu, L.; Li, X.; Huang, C.L.; Ma, M.G.; Che, T.; Bogaert, J.; Veroustraete, F.; Dong, Q.H.; Ceulemans, R. Investigating the relationship between ground-measured LAI and vegetation indices in an alpine meadow, North-West China. Int. J. Remote Sens. 2005, 26, 4471–4484. [Google Scholar] [CrossRef]
- Cannell, M.G.R. Physiological basis of wood production: A review. Scand. J. For. Res. 1989, 4, 459–490. [Google Scholar] [CrossRef]
- Myneni, R.B.; Ramakrishna, R.; Nemani, R.; Running, S.W. Estimation of global leaf area index and absorbed PAR using radiative transfer models. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1380–1393. [Google Scholar] [CrossRef]
- Alton, P.B.; Ellis, R.; Los, S.O.; North, P.R. Improved global simulations of gross primary product based on a separate and explicit treatment of diffuse and direct sunlight. J. Geophys. Res. 2007. [Google Scholar] [CrossRef]
- Valade, A.; Ciais, P.; Vuichard, N.; Viovy, N.; Caubel, A.; Huth, N.; Marin, F.; Martiné, J.F. Modeling sugarcane yield with a process-based model from site to continental scale: Uncertainties arising from model structure and parameter values. Geosci. Model Dev. 2014, 7, 1225–1245. [Google Scholar] [CrossRef]
- Wang, Q.; Tenhunen, J.; Falge, E.; Bernhofer, C.H.; Granier, A.; Vesala, T. Simulation and scaling of temporal variation in gross primary production for coniferous and deciduous temperate forests. Glob. Chang. Biol. 2003, 10, 37–51. [Google Scholar] [CrossRef]
- Kucharik, C.J.; Norman, J.M.; Murdock, L.M.; Gower, S.T. Characterizing canopy nonrandomness with a multiband vegetation imager (MVI). J. Geophys. Res. Biogeosci. 1997, 102, 29455–29473. [Google Scholar] [CrossRef]
- Adiku, S.; Reichstein, M.; Lohila, A.; Dinh, N.Q.; Aurela, M.; Laurila, T.; Lueers, J.; Tenhunen, J.D. PIXGRO: A model for simulating the ecosystem CO2 exchange and growth of spring barley. Ecol. Model. 2006, 190, 260–276. [Google Scholar] [CrossRef]
- Tague, C.L.; Band, L.E. Evaluating explicit and implicit routing for watershed hydro-ecological models of forest hydrology at the small catchment scale. Hydrol. Process. 2001, 15, 1415–1439. [Google Scholar] [CrossRef]
- Huete, A. A comparison of vegetation indices over a global set of TM images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Brantley, S.T.; Zinnert, J.C.; Young, D.R. Application of hyperspectral vegetation indices to detect variations in high leaf area index temperate shrub thicket canopies. Remote Sens. Environ. 2011, 115, 514–523. [Google Scholar] [CrossRef]
- Gamon, J.A.; Field, C.B.; Goulden, M.L.; Griffin, K.L.; Hartley, A.E.; Joel, G.; Peñuelas, J.; Valentini, R. Relationships between NDVI, canopy structure, and photosynthesis in three Californian vegetation types. Ecol. Appl. 1995, 5, 28–41. [Google Scholar] [CrossRef]
- Wang, Q.; Adiku, S.; Tenhunen, J.; Granier, A. On the relationship of NDVI with leaf area index in a deciduous forest site. Remote Sens. Environ. 2005, 94, 244–255. [Google Scholar] [CrossRef]
- Wardlow, B.D.; Egbert, S.L. A comparison of MODIS 250 m EVI and NDVI data for crop mapping: A case study for southwest Kansas. Int. J. Remote Sens. 2010, 31, 805–830. [Google Scholar] [CrossRef]
- Pan, Y.; Li, L.; Zhang, J.; Liang, S.; Zhu, X.; Sulla-Menashe, D. Winter wheat area estimation from MODIS-EVI time series data using the Crop Proportion Phenology Index. Remote Sens. Environ. 2012, 119, 232–242. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Atzberger, C.; Skidmore, A.K.; Abkar, A.A. Leaf Area Index derivation from hyperspectral vegetation indicesand the red edge position. Int. J. Remote Sens. 2009, 30, 6199–6218. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Wardlow, B.D.; Keydan, G.P.; Leavitt, B. An evaluation of MODIS 250 m data for green LAI estimation in crops. Geophys. Res. Lett. 2007. [Google Scholar] [CrossRef]
- Liu, J.; Pattey, E.; Jégo, G. Assessment of vegetation indices for regional crop green LAI estimation from Landsat images over multiple growing seasons. Remote Sens. Environ. 2012, 123, 347–358. [Google Scholar] [CrossRef]
- Ma, M.; Veroustraete, F.; Lu, L.; Li, X.; Ceulemans, R.; Bogaert, J.; Huang, C.; Che, T.; Dong, Q. Validating the MODIS LAI product by scaling up LAI measurements at a VALERI alpine meadow site, China. Proc. SPIE 2007. [Google Scholar] [CrossRef]
- Potithep, S.; Nasahara, N.K. What is the actual relationship between LAI and VI in a deciduous broadleaf forest? Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 1–6. [Google Scholar]
- Fan, L.; Gao, Y.; Brück, H.; Bernhofer, C. Investigating the relationship between NDVI and LAI in semi-arid grassland in Inner Mongolia using in-situ measurements. Theor. Appl. Climatol. 2008, 95, 151–156. [Google Scholar] [CrossRef]
- Xiao, X.; He, L.; Salas, W.; Li, C.; Moore, B., III; Zhao, R.; Frolking, S.; Boles, S. Quantitative relationships between field-measured leaf area index and vegetation index derived from VEGETATION images for paddy rice fields. Int. J. Remote Sens. 2002, 23, 3595–3604. [Google Scholar] [CrossRef]
- Wang, Q.; Tenhunen, J.; Dinh, N.Q.; Reichstein, M.; Vesala, T.; Keronen, P. Similarities in ground- and satellite-based NDVI time series and their relationship to physiological activity of a Scots pine forest in Finland. Remote Sens. Environ. 2004, 93, 225–237. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Haboudane, D. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Gupta, R.K.; Prasad, T.S.; Vijayan, D. Relationship between LAI and NDVI for IRS LISS and Landsat TM bands. Adv. Space Res. 2000, 26, 1047–1050. [Google Scholar] [CrossRef]
- Brando, P.M.; Goetz, S.J.; Baccini, A. Seasonal and interannual variability of climate and vegetation indices across the Amazon. Proc. Natl. Acad. Sci. USA 2010, 107, 14685–14690. [Google Scholar] [CrossRef] [PubMed]
- Darvishzadeh, R.; Skidmore, A.; Atzberger, C.; van Wieren, S. Estimation of vegetation LAI from hyperspectral reflectance data: Effects of soil type and plant architecture. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 358–373. [Google Scholar] [CrossRef]
- Spanner, M.A.; Pierce, L.L.; Running, S.W.; Peterson, D.L. The seasonality of AVHRR data of temperate coniferous forests: Relationship with leaf area index. Remote Sens. Environ. 1990, 33, 97–112. [Google Scholar] [CrossRef]
- IRRC. Irrigated Rice Research Consortium. Available online: http://irri.org/networks/irrigated-rice-research-consortium (accessed on 9 August 2016).
- Cassman, K.G.; Wood, S. Ecosystems and HumanWell-Being: Current State and Trends; Island Press: Washington, DC, USA, 2005; Volume 1, pp. 745–789. [Google Scholar]
- Smith, P.; Martino, D.; Cai, Z.; Gwary, D.; Janzen, H.; Kumar, P.; McCarl, B.; Ogle, S.; O’Mara, F.; Rice, C.; et al. Greenhouse gas mitigation in agriculture. Philos. Trans. R. Soc. B Biol. Sci. 2008, 363, 789–813. [Google Scholar] [CrossRef] [PubMed]
- Wilby, A.; Thomas, M.B. Biodiversity and the functioning of selected terrestrial ecosystems: Agricultural systems. In Biodiversity: Structure and Function; Eolss: Oxford, UK, 2005; pp. 151–163. [Google Scholar]
- Hatfield, J.L.; Prueger, J.H. Value of using different vegetative indices to quantify agricultural crop characteristics at different growth stages under varying management practices. Remote Sens. 2010, 2, 562–578. [Google Scholar] [CrossRef]
- Wattenbach, M.; Sus, O.; Vuichard, N.; Lehuger, S.; Gottschalk, P.; Li, L.; Leip, A.; Williams, M.; Tomelleri, E.; Kutsch, W.L.; et al. The carbon balance of European croplands: A cross-site comparison of simulation models. Agric. Ecosyst. Environ. 2010, 139, 419–453. [Google Scholar] [CrossRef]
- FAOSTAT. Statistical Database of the Food and Agriculture Organization of the United Nations. Available online: http://faostat.fao.org/ (accessed on 9 August 2016).
- Arnhold, S.; Lindner, S.; Lee, B.; Martin, E.; Kettering, J.; Nguyen, T.T.; Koellner, T.; Ok, Y.S.; Huwe, B. Conventional and organic farming: Soil erosion and conservation potential for row crop cultivation. Geoderma 2014, 219–220, 89–105. [Google Scholar] [CrossRef]
- Choi, G.Y.; Lee, B.R.; Kang, S.K.; Tenhunen, J. Variations of summertime temperature lapse rate within a mountainous basin in the Republic of Korea—A case study of Punch Bowl, Yanggu in 2009–2010. J. Korean Assoc. Reg. Geogr. 2010, 16, 339–355. [Google Scholar]
- Saito, M.; Miyata, A.; Nagai, H.; Yamada, T. Seasonal variation of carbon dioxide exchange in rice paddy field in Japan. Agric. For. Meteorol. 2005, 135, 93–109. [Google Scholar] [CrossRef]
- Kim, H.; Lieffering, M.; Kobayashi, K. Seasonal changes in the effects of elevated CO2 on rice at three levels of nitrogen supply: A free air CO2 enrichment (FACE) experiment. Glob. Chang. Biol. 2003, 9, 826–837. [Google Scholar] [CrossRef]
- Maruyama, A.; Kuwagata, T.; Ohba, K.; Maki, T. Dependence of solar radiation transport in rice canopies on developmental stage. Jpn. Agric. Res. Quart. 2007, 41, 39–45. [Google Scholar] [CrossRef]
- Maruyama, A.; Kuwagata, T. Diurnal and seasonal variation in bulk stomatal conductance of the rice canopy and its dependence on developmental stage. Agric. For. Meteorol. 2008, 148, 1161–1173. [Google Scholar] [CrossRef]
- Maruyama, A.; Kuwagata, T. Coupling land surface and crop growth models to estimate the effects of changes in the growing season on energy balance and water use of rice paddies. Agric. For. Meteorol. 2010, 150, 919–930. [Google Scholar] [CrossRef]
- Kutsch, W.L.; Aubinet, M.; Buchmann, N.; Smith, P.; Osborne, B.; Eugster, W.; Wattenbach, M.; Schrumpf, M.; Schulze, E.D.; Tomelleri, E. The net biome production of full crop rotations in Europe. Agric. Ecosyst. Environ. 2010, 139, 336–345. [Google Scholar] [CrossRef]
- Moors, E.J.; Jacobs, C.; Jans, W.; Supit, I.; Kutsch, W.L.; Bernhofer, C.; Béziat, P.; Buchmann, N.; Carrara, A.; Ceschia, E. Variability in carbon exchange of European croplands. Agric. Ecosyst. Environ. 2010, 139, 325–335. [Google Scholar] [CrossRef]
- Warehouse Inventory Search Tool (WIST). Available online: https://wist.echo.nasa.gov/ (accessed on 9 August 2016).
- Miyata, A.; Leuning, R.; Denmead, O.T.; Kim, J.; Harazono, Y. Carbon dioxide and methane fluxes from an intermittently flooded paddy field. Agric. For. Meteorol. 2000, 102, 287–303. [Google Scholar] [CrossRef]
- Jonsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
- Schafer, R.W. What is a savitzky-golay filter? [lecture notes]. IEEE Signal Process. Mag. 2011, 28, 111–117. [Google Scholar] [CrossRef]
- Pontailler, J.Y.; Hymus, G.J.; Drake, B.G. Estimation of leaf area index using ground-based remote sensed NDVI measurements: Validation and comparison with two indirect techniques. Can. J. Remote Sens. 2003, 29, 381–387. [Google Scholar] [CrossRef]
- Stenberg, P.; Rautiainen, M.; Manninen, T.; Voipio, P.; Smolander, H. Reduced simple ratio better than NDVI for estimating LAI in Finnish pine and spruce stands. Silva Fenn. 2004, 38, 3–14. [Google Scholar] [CrossRef]
- Muraoka, H.; Koizumi, H. Photosynthetic and structural characteristics of canopy and shrub trees in a cool-temperate deciduous broadleaved forest: Implication to the ecosystem carbon gain. Agric. For. Meteorol. 2005, 134, 39–59. [Google Scholar] [CrossRef]
- Muraoka, H.; Koizumi, H. Leaf and shoot ecophysiological properties and their role in photosynthetic carbon gain of cool-temperate deciduous forest trees. Elsevier Oceanogr. Ser. 2007, 73, 417–443. [Google Scholar]
- Lu, L.; Li, X.; Ma, M.G.; Che, T.; Huang, C.L.; Bogaert, J.; Veroustraete, F.; Dong, Q.H.; Ceulemans, R. Investigating relationship between landsat ETM+ data and LAI in a semi-arid grassland of Northwest China. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; pp. 3622–3625.
- Hastie, T.; Tibshirani, R. Exploring the nature of covariate effects in the proportional hazards model. Biometrics 1990, 46, 1005–1016. [Google Scholar] [CrossRef] [PubMed]
- Liu, H. Generalized Additive Model. Ph.D. Thesis, University of Minnesota Duluth, Duluth, MN, USA, 2008. [Google Scholar]
- Yee, T.W.; Mitchell, N.D. Generalized additive models in plant ecology. J. Veg. Sci. 1991, 2, 587–602. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Generalized additive models. Stat. Sci. 1986, 1, 297–310. [Google Scholar] [CrossRef]
- Muraoka, H.; Noda, H.M.; Nagai, S.; Motohka, T.; Saitoh, T.M.; Nasahara, K.N.; Saigusa, N. Spectral vegetation indices as the indicator of canopy photosynthetic productivity in a deciduous broadleaf forest. J. Plant Ecol. 2013, 6, 393–407. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Sims, D.A.; Rahman, A.F.; Cordova, V.D.; El-Masri, B.Z.; Baldocchi, D.D.; Flanagan, L.B.; Goldstein, A.H.; Hollinger, D.Y.; Misson, L.; Monson, R.K.; et al. On the use of MODIS EVI to assess gross primary productivity of North American ecosystems. J. Geophys. Res. 2006. [Google Scholar] [CrossRef]
- Tan, B.; Morisette, J.T.; Wolfe, R.E.; Gao, F.; Ederer, G.A.; Nightingale, J.; Pedelty, J.A. An enhanced TIMESAT algorithm for estimating vegetation phenology metrics from MODIS data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 361–371. [Google Scholar] [CrossRef]
- Wardlow, B.D.; Kastens, J.H.; Egbert, S.L. Using USDA crop progress data for the evaluation of greenup onset date calculated from MODIS 250 meter data. Photogramm. Eng. Remote Sens. 2006, 72, 1225–1234. [Google Scholar] [CrossRef]









| Site | Year | P | Transplanting Date | Harvest Date | |||
|---|---|---|---|---|---|---|---|
| (MJ/) | () | (mm) | (DOY) | (DOY) | |||
| Haean | 2010 | 1713 | 20.4 | 1165 | 144 | 290 | 5.8 |
| Mase | 2002 | 2356 | 22.0 | 593 | 122 | 262 | 5.5 |
| 2003 | 2049 | 20.3 | 545 | 122 | 262 | 5.1 | |
| 2004 | 2384 | 22.7 | 547 | 123 | 254 | 4.9 | |
| 2005 | 2237 | 21.8 | 647 | 122 | 256 | 4.4 | |
| 2006 | 1989 | 21.5 | 632 | 122 | 141 | 6.0 | |
| El Saler | 2007 | 3224 | 22.8 | 437 | 134 | 270 | 5.7 |
| 2008 | 3263 | 22.1 | 121 | 132 | 278 | 6.1 | |
| Shizukuishi | 2000 | 2057 | 21.4 | 615 | 143 | 263 | 4.5 |
| Aso | 2003 | 2176 | 21.4 | 1491 | 138 | 268 | 3.5 |
| Site | Year | Growth Phase | NDVI | EVI | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Regression Equation | RMSE | p | Regression Equation | RMSE | p | ||||||
| HK | 2010 | Entire | y = | 0.83 | 0.82 | 0.003 | y = | 0.72 | 1.06 | 0.01 | |
| MSE | 2002–2005 | Entire | y = | 0.63 | 1.56 | <0.001 | y = | 0.62 | 4.41 | <0.005 | |
| ESES2 | 2007–2008 | Entire | y = | 0.67 | 1.27 | <0.001 | y = | 0.72 | 1.98 | <0.005 | |
| HK | 2010 | Before | y = | 0.90 | 1.21 | 0.009 | y = | 0.96 | 0.32 | 0.01 | |
| After | - | - | - | - | y = | 0.97 | 0.3 | 0.08 | |||
| MSE | 2002–2005 | Before | y = | 0.82 | 0.94 | <0.005 | y = | 0.72 | 6.63 | <0.005 | |
| After | y = | 0.42 | 0.78 | 0.007 | y = | 0.01 | 1.13 | 0.4 | |||
| ESES2 | 2007–2008 | Before | y = | 0.84 | 0.84 | <0.005 | y = | 0.88 | 1.22 | <0.005 | |
| After | y = | 0.93 | 0.24 | <0.005 | y = | 0.73 | 0.53 | 0.009 | |||
| Asia | 2002–2010 | Before | Y = | 0.80 | 0.97 | <0.005 | y = | 0.61 | 3.43 | <0.005 | |
| After | y = | 0.27 | 0.93 | 0.02 | y = | 0.05 | 1.3 | 0.2 | |||
| Asia & Europe | 2002–2010 | Before | y = | 0.76 | 1.03 | <0.005 | y = | 0.66 | 2.88 | <0.005 | |
| After | y = | 0.36 | 0.85 | 0.001 | y = | 0.14 | 1.2 | 0.05 | |||
| VI | Site | Year | Consistent Development Curve | Exponential Regression | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | CV (%) | p | RMSE | CV (%) | p | ||||||
| NDVI | HK | 2010 | 0.78 | 0.89 | 59.08 | <0.005 | 0.75 | 0.93 | 57.12 | <0.005 | |
| MSE | 2002 | 0.90 | 0.38 | 23.18 | <0.005 | 0.65 | 1.19 | 59.25 | <0.005 | ||
| 2003 | 0.90 | 0.33 | 22.41 | <0.005 | 0.24 | 0.84 | 56.44 | <0.005 | |||
| 2004 | 0.92 | 0.21 | 11.49 | <0.005 | 0.75 | 1.30 | 56.37 | <0.005 | |||
| 2005 | 0.95 | 0.77 | 41.92 | <0.005 | 0.89 | 0.37 | 28.00 | <0.005 | |||
| 2006 | 0.92 | 0.57 | 25.11 | <0.005 | |||||||
| ESES2 | 2007 | 0.92 | 0.77 | 27.46 | <0.005 | 0.68 | 0.65 | 54.22 | <0.005 | ||
| 2008 | 0.93 | 0.72 | 23.77 | <0.005 | 0.60 | 0.37 | 57.85 | <0.005 | |||
| Shizukuishi | 2000 | 0.98 | 0.54 | 19.42 | <0.005 | ||||||
| Aso | 2003 | 0.98 | 0.77 | 41.79 | <0.005 | ||||||
| EVI | HK | 2010 | 0.73 | 1.19 | 73.38 | 0.008 | 0.56 | 1.11 | 69.45 | 0.03 | |
| MSE | 2002 | 0.93 | 0.39 | 21.00 | <0.005 | 0.86 | 1.57 | 69.53 | <0.005 | ||
| 2003 | 0.96 | 0.20 | 14.48 | <0.005 | 0.74 | 1.54 | 57.30 | <0.005 | |||
| 2004 | 0.91 | 0.23 | 11.90 | <0.005 | 0.85 | 1.22 | 43.22 | <0.005 | |||
| 2005 | 0.88 | 0.64 | 42.93 | <0.005 | 0.68 | 5.76 | 342.96 | <0.005 | |||
| 2006 | 0.86 | 0.69 | 31.70 | <0.005 | |||||||
| ESES2 | 2007 | 0.89 | 0.82 | 29.25 | <0.005 | 0.64 | 1.63 | 90.44 | 0.01 | ||
| 2008 | 0.88 | 0.82 | 27.43 | <0.005 | 0.69 | 1.04 | 40.86 | <0.005 | |||
| Shizukuishi | 2000 | 0.97 | 0.57 | 20.41 | 0.01 | ||||||
| Aso | 2003 | 0.98 | 0.72 | 39.73 | <0.005 | ||||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, B.; Kwon, H.; Miyata, A.; Lindner, S.; Tenhunen, J. Evaluation of a Phenology-Dependent Response Method for Estimating Leaf Area Index of Rice Across Climate Gradients. Remote Sens. 2017, 9, 20. https://doi.org/10.3390/rs9010020
Lee B, Kwon H, Miyata A, Lindner S, Tenhunen J. Evaluation of a Phenology-Dependent Response Method for Estimating Leaf Area Index of Rice Across Climate Gradients. Remote Sensing. 2017; 9(1):20. https://doi.org/10.3390/rs9010020
Chicago/Turabian StyleLee, Bora, Hyojung Kwon, Akira Miyata, Steve Lindner, and John Tenhunen. 2017. "Evaluation of a Phenology-Dependent Response Method for Estimating Leaf Area Index of Rice Across Climate Gradients" Remote Sensing 9, no. 1: 20. https://doi.org/10.3390/rs9010020
APA StyleLee, B., Kwon, H., Miyata, A., Lindner, S., & Tenhunen, J. (2017). Evaluation of a Phenology-Dependent Response Method for Estimating Leaf Area Index of Rice Across Climate Gradients. Remote Sensing, 9(1), 20. https://doi.org/10.3390/rs9010020