An Improved Estimation of Regional Fractional Woody/Herbaceous Cover Using Combined Satellite Data and High-Quality Training Samples
Abstract
:1. Introduction
- Multiple satellite data combined and used as RF model inputs for estimation; and
- High-quality training samples of representative based on a spatial sampling layout formed by a tailored sampling strategy.
2. Materials and Methods
2.1. The Study Area
2.2. Data Handling and Methods
- A suite of statistics and metrics of satellite data from multiple sources were pre-processed into a uniform format as the predictor variable pool;
- Training data were prepared using a sampling strategy and a human-machine interactive classification method; and
- RF models were developed with different predictor sets to find out the most appropriate combination of predictor inputs.
2.2.1. Predictor Data Pre-processing
2.2.2. Training Data Preparation
- We first divided the whole study area into four independent zones by its patterns of environmental features and land-use intensity (domain knowledge); and
- After division, a two-phase sampling was used to form a spatial sampling layout to determine final sample locations. That is, simple random sampling (SRS) was used to select primary grids in each zone. Then final sample locations were confirmed using systematic sampling (SYS) in each primary grid.
2.3. Building Random Forests
2.4. Field Validation
3. Results
3.1. Experiments with Predictor Variables
3.2. Mapping Results
3.3. Validation with Field Data
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- DeFries, R.; Achard, F.; Brown, S.; Herold, M.; Murdiyarso, D.; Schlamadinger, B.; de Souza, C. Earth observations for estimating greenhouse gas emissions from deforestation in developing countries. Environ. Sci. Policy 2007, 10, 385–394. [Google Scholar] [CrossRef]
- Yang, J.; Weisberg, P.J.; Bristow, N.A. Landsat remote sensing approaches for monitoring long-term tree cover dynamics in semi-arid woodlands: Comparison of vegetation indices and spectral mixture analysis. Remote Sens. Environ. 2012, 119, 62–71. [Google Scholar] [CrossRef]
- Harris, A.; Carr, A.S.; Dash, J. Remote sensing of vegetation cover dynamics and resilience across southern Africa. Int. J. Appl. Earth Observ. Geoinf. 2014, 28, 131–139. [Google Scholar] [CrossRef]
- Liu, H.; Cui, H.; Pott, R.; Speier, M. Vegetation of the woodland-steppe transition at the southeastern edge of the Inner Mongolian Plateau. J. Veg. Sci. 2000, 11, 525–532. [Google Scholar] [CrossRef]
- Archer, S. Tree-grass dynamics in a thornscrub savanna parkland: Reconstructing the past and predicting the future. Ecoscience 2016, 2, 83–99. [Google Scholar] [CrossRef]
- Yu, K.; D’Odorico, P. Hydraulic lift as a determinant of tree-grass coexistence on savannas. New Phytol. 2015, 207, 1038–1051. [Google Scholar] [CrossRef] [PubMed]
- Brazier, R.E.; Turnbull, L.; Wainwright, J.; Bol, R. Carbon loss by water erosion in drylands: Implications from a study of vegetation change in the south-west USA. Hydrol. Process. 2014, 28, 2212–2222. [Google Scholar] [CrossRef] [Green Version]
- Sitch, S.; Friedlingstein, P.; Gruber, N.; Jones, S.D.; Murray-Tortarolo, G.; Ahlström, A.; Doney, S.C.; Graven, H.; Heinze, C.; Huntingford, C.; et al. Recent trends and drivers of regional sources and sinks of carbon dioxide. Biogeosciences 2015, 12, 653–679. [Google Scholar] [CrossRef] [Green Version]
- Elmendorf, S.C. Global assessment of experimental climate warming on tundra vegetation: Heterogeneity over space and time. Ecol. Lett. 2014, 15, 164–175. [Google Scholar] [CrossRef] [PubMed]
- Gessner, U.; Machwitz, M.; Conrad, C.; Dech, S. Estimating the fractional cover of growth forms and bare surface in savannas. A multi-resolution approach based on regression tree ensembles. Remote Sens. Environ. 2013, 129, 90–102. [Google Scholar] [CrossRef] [Green Version]
- Okin, G.S.; Clarke, K.D.; Lewis, M.M. Comparison of methods for estimation of absolute vegetation and soil fractional cover using modis normalized brdf-adjusted reflectance data. Remote Sens. Environ. 2013, 130, 266–279. [Google Scholar] [CrossRef]
- Fluet-Chouinard, E.; Lehner, B.; Rebelo, L.M.; Papa, F.; Hamilton, S.K. Development of a global inundation map at high spatial resolution from topographic downscaling of coarse-scale remote sensing data. Remote Sens. Environ. 2015, 158, 348–361. [Google Scholar] [CrossRef]
- Mishra, N.B.; Crews, K.A.; Okin, G.S. Relating spatial patterns of fractional land cover to savanna vegetation morphology using multi-scale remote sensing in the Central Kalahari. Int. J. Remote Sens. 2014, 35, 2082–2104. [Google Scholar]
- Brandt, M.; Hiernaux, P.; Tagesson, T.; Verger, A.; Rasmussen, K.; Diouf, A.A.; Mbow, C.; Mougin, E.; Fensholt, R. Woody plant cover estimation in drylands from Earth Observation based seasonal metrics. Remote Sens. Environ. 2016, 172, 28–38. [Google Scholar] [CrossRef]
- DiMiceli, C.M.; Carroll, M.L.; Sohlberg, R.A.; Huang, C.; Hansen, M.C.; Townshend, J.R.G. Annual Global Automated MODIS Vegetation Continuous Fields (MOD44B) at 250 m Spatial Resolution for Data Years Beginning Day 65, 2000–2010, Collection 5 Percent Tree Cover; University of Maryland: College Park, MD, USA, 2011. [Google Scholar]
- Medina, E.; Cuevas, E.; Molina, S.; Luco, A.E.; Ramos, O. Structural variability and species diversity of a dwarf caribbean dry forest. Caribb. J. Sci. 2012, 46, 203–215. [Google Scholar] [CrossRef]
- Ma, L.; Zhou, Y.; Chen, J.; Cao, X.; Chen, X.H. Estimation of fractional vegetation cover in semiarid areas by integrating endmember reflectance purification into nonlinear spectral mixture analysis. IEEE Geosci. Remote Sens. 2015, 12, 1175–1179. [Google Scholar]
- Chopping, M.; Su, L.; Rango, A.; Martonchik, J.V.; Peters, D.P.C.; Laliberte, A. Remote sensing of woody shrub cover in desert grasslands using MISR with a geometric-optical canopy reflectance model. Remote Sens. Environ. 2008, 112, 19–34. [Google Scholar] [CrossRef]
- Johnson, B.; Tateishi, R.; Kobayashi, T. Remote sensing of fractional green vegetation cover using spatially-interpolated endmembers. Remote Sens. 2012, 4, 2619–2634. [Google Scholar] [CrossRef]
- Brown, J.F.; Howard, D.; Wylie, B.; Frieze, A.; Ji, L.; Gacke, C. Application-ready expedited MODIS data for operational land surface monitoring of vegetation condition. Remote Sens. 2015, 7, 16226–16240. [Google Scholar] [CrossRef]
- Hansen, M.C.; Townshend, J.R.G.; Defries, R.S.; Carroll, M. Estimation of tree cover using modis data at global, continental and regional/local scales. Int. J. Remote Sens. 2005, 26, 4359–4380. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, H.Y.; He, S.Y.; Zhao, F.J.; Zhu, J.L.; Wang, H.Y.; Liu, G.; Wu, X.C. Patterns of local and regional grain size distribution and their application to holocene climate reconstruction in semi-arid Inner Mongolia, China. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2011, 307, 168–176. [Google Scholar] [CrossRef]
- Clark, M.L.; Aide, T.M.; Grau, H.R.; Riner, G. A scalable approach to mapping annual land cover at 250 m using MODIS time series data: A case study in the Dry Chaco ecoregion of South America. Remote Sens. Environ. 2010, 114, 2816–2832. [Google Scholar] [CrossRef]
- Avitabile, V.; Baccini, A.; Friedl, M.A.; Schmullius, C. Capabilities and limitations of landsat and land cover data for aboveground woody biomass estimation of Uganda. Remote Sens. Environ. 2012, 117, 366–380. [Google Scholar] [CrossRef]
- Peters, D. Future Directions in Jornada Research: Applying an Interactive Landscape Model to Solve Problems. In Structure and Function of a Chihuahuan Desert Ecosystem: The Jornada Basin Long-Term Ecological Research Site; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Liu, H.Y.; He, S.Y.; Anenkhonov, O.A.; Hu, G.Z.; Sandanov, D.V.; Badmaeva, N.K. Topography-controlled soil water content and the coexistence of forest and steppe in Northern China. Phys. Geogr. 2012, 33, 561–573. [Google Scholar] [CrossRef]
- Liu, S.L.; Wang, T.; Guo, J.; Qu, J.J.; An, P.J. Vegetation change based on SPOT-VGT data from 1998–2007, northern China. Environ. Earth Sci. 2010, 60, 1459–1466. [Google Scholar] [CrossRef]
- Sternberg, T. Piospheres and pastoralists: Vegetation and degradation in steppe grasslands. Hum. Ecol. 2012, 40, 811–820. [Google Scholar] [CrossRef]
- Bai, Y.F.; Han, X.G.; Wu, J.G.; Chen, Z.Z.; Li, L.H. Ecosystem stability and compensatory effects in the Inner Mongolia grassland. Nature 2004, 431, 181–184. [Google Scholar] [CrossRef] [PubMed]
- Clark, M.L.; Roberts, D.A.; Ewel, J.J.; Clark, D.B. Estimation of tropical rain forest aboveground biomass with small-footprint lidar and hyperspectral sensors. Remote Sens. Environ. 2011, 115, 2931–2942. [Google Scholar] [CrossRef]
- Oh, Y.; Kwon, S.G.; Hwang, J.H. Soil moisture detection using kompsat-5 sar data. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 1250–1253.
- Wang, J.F.; Christakos, G.; Hu, M.G. Modeling spatial means of surfaces with stratified nonhomogeneity. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4167–4174. [Google Scholar] [CrossRef]
- Christakos, G. Methodological developments in geophysical assimilation modeling. Rev. Geophys. 2005, 43. [Google Scholar] [CrossRef]
- Daschiel, H.; Datcu, M. Information mining in remote sensing image archives: System evaluation. IEEE Trans. Geosci. Remote Sens. 2005, 43, 188–199. [Google Scholar] [CrossRef]
- Lindgren, K. An information-theoretic perspective on coarse-graining, including the transition from micro to macro. Entropy 2015, 17, 3332–3351. [Google Scholar] [CrossRef]
- Yang, W.Z.; Ni-Meister, W.; Lee, S. Assessment of the impacts of surface topography, off-nadir pointing and vegetation structure on vegetation lidar waveforms using an extended geometric optical and radiative transfer model. Remote Sens. Environ. 2011, 115, 2810–2822. [Google Scholar] [CrossRef]
- Doerr, D.; Gronau, I.; Moran, S.; Yavneh, I. Stochastic errors vs. modeling errors in distance based phylogenetic reconstructions. Algorithms Mol. Biol. 2012, 7. [Google Scholar] [CrossRef] [PubMed]







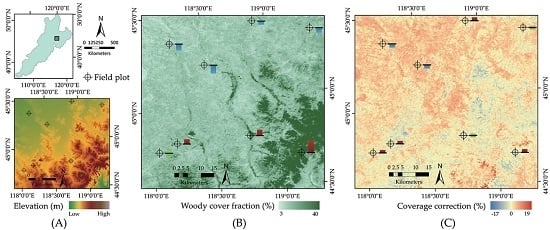
 overestimates,
overestimates,  underestimates, and
underestimates, and  is as close to the woody cover fraction observed in the field. We can see that the optimal model results are closer to field values and the correction for deviation express regional heterogeneity.
is as close to the woody cover fraction observed in the field. We can see that the optimal model results are closer to field values and the correction for deviation express regional heterogeneity.
 overestimates,
overestimates,  underestimates, and
underestimates, and  is as close to the woody cover fraction observed in the field. We can see that the optimal model results are closer to field values and the correction for deviation express regional heterogeneity.
is as close to the woody cover fraction observed in the field. We can see that the optimal model results are closer to field values and the correction for deviation express regional heterogeneity.
| Type | Variables | Brief Introduction | Source | Original Spatial Resolution |
|---|---|---|---|---|
| Vegetation Index | NDVI/EVI | Represent growing conditions of plants | LP DAAC MODIS 13Q1 | 250 m |
| Optical Reflectance | Blue/red/NIR/MIR | Used to distinguish the features of vegetation and non-vegetation | 250 m | |
| Bioclimatic variables | Temperature/precipitation statistics | Provide annual trends, seasonality and extreme environmental factors | Worldclim data library | 30 arc seconds (≈1 km) |
| Topographic Information | elevation | Represent micro-relief conditions of plants | CGIAR-CSI STRM 90 m DEM | 3 arc seconds (≈90 m) |
| slope/aspect | IIASA-Global Terrain Slope and Aspect Data | 30 arc seconds | ||
| Land Surface Information | soil type | Provide plant forms and vegetation phenology information | Harmonized World Soil Database (HWSD) | 30 arc seconds |
| land cover type | ESA GlobCover | 300 m |
| Variable Set | Woody Vegetation | Herbaceous Vegetation | ||
|---|---|---|---|---|
| Bias | NMSE | Bias | NMSE | |
| Set 1: vegetation and reflectance indices | 0.65 | 0.560 | 2.09 | 0.772 |
| Set 2: Set 1 + land-cover and soil type | 0.81 | 0.539 | 2.18 | 0.745 |
| Set 3: Set 1 + bioclimatic variables | 0.85 | 0.495 | 1.21 | 0.658 |
| Set 4: Set 1 + topographic variables | 0.80 | 0.574 | 0.74 | 0.710 |
| Set 5: Set 2 + bioclimatic variables | 0.53 | 0.491 | 0.78 | 0.643 |
| Set 6: Set 2 + topographic variables | 0.86 | 0.532 | 1.05 | 0.700 |
| Set 7: Set 3 + topographic variables | 0.44 | 0.491 | 0.68 | 0.683 |
| Set 8: All variables | 0.42 | 0.469 | 0.72 | 0.650 |
| Variable Type | Woody Vegetation | Herbaceous Vegetation |
|---|---|---|
| Optical reflectance (20) | 109.3 | 114.8 |
| Vegetation index (10) | 53.4 | 84.5 |
| Bioclimatic information (19) | 126.6 | 137.9 |
| Topographic information (5) | 22.8 | - |
| Land surface information (2) | 11.3 | 3.12 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Liu, H.; Qiu, S.; Wu, X.; Tian, Y.; Hao, Q. An Improved Estimation of Regional Fractional Woody/Herbaceous Cover Using Combined Satellite Data and High-Quality Training Samples. Remote Sens. 2017, 9, 32. https://doi.org/10.3390/rs9010032
Liu X, Liu H, Qiu S, Wu X, Tian Y, Hao Q. An Improved Estimation of Regional Fractional Woody/Herbaceous Cover Using Combined Satellite Data and High-Quality Training Samples. Remote Sensing. 2017; 9(1):32. https://doi.org/10.3390/rs9010032
Chicago/Turabian StyleLiu, Xu, Hongyan Liu, Shuang Qiu, Xiuchen Wu, Yuhong Tian, and Qian Hao. 2017. "An Improved Estimation of Regional Fractional Woody/Herbaceous Cover Using Combined Satellite Data and High-Quality Training Samples" Remote Sensing 9, no. 1: 32. https://doi.org/10.3390/rs9010032
APA StyleLiu, X., Liu, H., Qiu, S., Wu, X., Tian, Y., & Hao, Q. (2017). An Improved Estimation of Regional Fractional Woody/Herbaceous Cover Using Combined Satellite Data and High-Quality Training Samples. Remote Sensing, 9(1), 32. https://doi.org/10.3390/rs9010032