1. Introduction
Hyperspectral remote sensing usually collects reflectance information of objects in hundreds of contiguous bands over a certain electromagnetic spectrum. It collects images with a very high spectral resolution, enabling a fine discrimination of different objects by their spectral signatures. However, due to the limitation of imaging sensor technologies, signal to noise ratio (SNR) and time constraints, there exists a trade-off between the spatial resolution and spectral resolution. Consequently, hyperspectral images (HSIs) are often acquired under a relatively low spatial resolution, degrading their performance in practical applications, including mineralogy, manufacturing and surveillance. Therefore, it is highly desirable to increase the spatial resolution of HSIs via post-processing.
In general, there are several ways to improve spatial resolution of HSIs: (1) image fusion with other high-spatial-resolution sources; (2) sub-pixel based analysis; and (3) single-image super-resolution (SR). The first two approaches have been widely exploited in hyperspectral applications. When an auxiliary image with a higher spatial resolution is available, such as a panchromatic image or multispectral image, image fusion can be applied for spatial-resolution enhancement. Statistics based fusion techniques are firstly proposed, such as maximum a posteriori (MAP) estimation, stochastic mixing model based method, etc. [
1,
2,
3]. Recently, dictionary-based fusion methods dominate hyperspectral and multispectral image fusion, including spectral dictionary [
4,
5,
6] and spatial dictionary based methods, but they cannot effectively utilize both spatial and spectral information equally. The Spatial–Temporal remotely sensed Images and land cover Maps Fusion Model (STIMFM) was proposed to produce land cover maps at both fine spatial and temporal resolutions using a series of coarse spatial resolution images together with a few fine spatial resolution land cover maps that pre- and post-date the series of coarse spatial resolution images [
7]. The major limitation in these fusion techniques for HSI spatial-resolution enhancement is that an auxiliary co-registered image with a higher spatial resolution is required, which may be unavailable in practice.
Sub-pixel based analysis aims to exploit the information in the area covered by a pixel for different applications. Spectral mixture analysis (SMA) intends to estimate fractional abundance of pure ground objects within a mixed pixel [
8]. Such analysis can be fulfilled by extracting endmembers [
9,
10] and estimating their fractional abundance [
11] separately, or treating these two problems simultaneously as a blind signal decomposition problem, for which non-negative matrix factorization (NMF) [
12,
13], convex optimization [
14], and Neural Network (NN) based techniques [
15] are widely used. Sub-pixel level target detection has also been proposed to detect objects of interest within a pixel [
16,
17]. Soft-classification can be an option to handle the classification problem of low-spatial-resolution HSI [
18]. Recently, sub-pixel mapping (SPM) techniques, which predict the location of land cover classes within a coarse pixel (mixed pixel) [
19,
20], have also been proposed to generate a high-resolution classification map using fractional abundance images. Various methods based on linear optimization technique [
21], pixel/sub-pixel spatial attraction model [
22], pixel swapping algorithm [
23], maximum a posteriori (MAP) model [
24,
25], Markov random field (MRF) [
26,
27], artificial neural network (ANN) [
28,
29,
30], simulated annealing [
31], total variant model [
32], support vector regression [
33], and collaborative representation [
34] are proposed. In general, sub-pixel based analysis only overcomes the limitation in spatial-resolution for certain applications, e.g., classification and target detection.
Single-image SR, which aims to reconstruct a high-spatial-resolution image only from a low-spatial-resolution image, can break the limitation of the inherent spatial resolution in hyperspectral imaging systems without any other prior or auxiliary information. The basic method of single-image SR is through a traditional linear interpolator, such as bilinear and bicubic interpolation. However, these methods often lead to edge blur, and a jagged and ringing effect. Villa et al. [
35] attempted to split pixels into sub-pixels according to a zoom factor and to find the sub-pixel positions. However, sub-pixels are assumed to be pure pixels which may not be a reasonable assumption. In the past decades, the SR of traditional color images has gained great attention and many algorithms have been developed, such as iterative back projection (IBP) based on reconstruction [
36,
37] and sparse representation based algorithms [
38,
39]. Recently, deep learning based methods have been applied to the SR of color images and demonstrated to be of great superiority [
40,
41,
42]. Deep convolutional NN (CNN) is designed to directly learn an end-to-end mapping between low- and high-spatial-resolution images [
40]. The CNN has also been extended to a very deep version to explore contextual information over large image scenes by cascading small filters many times in a deep network structure [
43]. These CNNs for the SR of color images can be directly applied to HSIs for spatial SR in a band-by-band or 3-band-group manner. For example, the msiSRCNN algorithm extended the SRCNN in [
42] to spatial SR of multispectral images [
44]. However, spectral distortion is often induced in such extensions since spectral correlation in contiguous bands is ignored. Recently, Li et al. applied CNN to the SR of the spectral difference in HSIs to preserve the spectral information [
45,
46]. The spatial constraint or spatial-error-correction model are also imposed to further correct the spatial error in the SR process. However, the spatial down-sampling function (i.e., spatial filter) is required as complemental information in the training process.
Recently, CNN has also been attempted to the SR of HSIs in the spectral dimension [
47], demonstrating the feasibility and superiority of convolution to spectral dimension. Therefore, in order to alleviate spectral distortion by extending existing CNN based SR algorithms to HSIs, effectively utilizing both spatial context and spectral discrimination is of crucial importance. Such integration of spatial context and spectral discrimination has been demonstrated to be of great superiority in many hyperspectral applications, e.g., noise removal [
48,
49], classification [
50,
51], and SR [
52]. In CNN based hyperspectral applications, Makantasis et al. integrated spatial-spectral information into CNN using a randomized principal component analysis (RPCA) [
53]. However, the spatial-spectral features fed to CNN using RPCA cannot be directly extended for SR applications due to information loss. The 3D convolution has been demonstrated to be very effective to explore volumetric data [
54,
55,
56,
57] and successfully applied to HSIs to explore both spatial context and spectral discrimination for classification [
58]. Therefore, in order to explore both spatial context and spectral discrimination for spatial SR of HSIs, a three-dimensional full CNN (3D-FCNN) framework is proposed. Specifically, the 3D convolution operation is used to explore both spatial context between neighboring pixels and spectral correlation in adjacent band images so that spectral distortion is alleviated. In order to avoid the requirement of a large amount of labelled samples to train such a 3D-FCNN, a sensor-specific manner is designed such that the 3D-FCNN trained on a certain HSI can be directly applied for the SR of other HSIs acquired by the same sensor. Finally, extensive experiments on four HSIs acquired by two well-known hyperspectral sensors, namely HYDICE and ROSIS sensors, are carried out to demonstrate the effectiveness of the proposed algorithms for spatial SR of HSIs.
In summary, the main contributions of this work can be summarized as follows:
- (1)
A 3D-FCNN architecture is designed to directly learn an end-to-end mapping between low spatial-resolution and high spatial-resolution HSIs. Specifically, a 3D convolution operation is designed to explore both the spatial context between neighboring pixels and the spectral correlation in adjacent band images so that the spectral distortion is alleviated.
- (2)
A sensor-specific manner is designed for the proposed 3D-FCNN to avoid the requirement of a large amount of training samples from the target scene, such that a well-trained 3D-FCNN model from an HSI can be directly applied for spatial SR of other HSIs acquired by the same sensor.
The rest of this paper is organized as follows: our proposed 3D-FCNN architecture for spatial SR of HSIs is proposed in
Section 2. The experimental results on HSIs acquired by different sensors are reported in
Section 3. Finally, discussions and conclusions are presented in
Section 4 and
Section 5, respectively.
2. Materials and Methods
Deep learning networks have achieved great success in the SR of color images. For example, SRCNN [
42] aims at learning an end-to-end mapping by taking low spatial-resolution images as input and directly outputs the high spatial-resolution of the input image. However, the 2D convolutional layer utilized in SRCNN mainly takes the spatial information into consideration. When these networks are directly used for SR of HSIs in a band-by-band manner (or three bands treated as a false color image), e.g., msiSRCNN [
44], it easily results in spectral distortion because the strong spectral correlation in HSIs is ignored. Therefore, in order to maintain the spectral fidelity of HSIs after spatial SR, both spatial context of adjacent pixels and spectral correlation among neighboring bands should be considered.
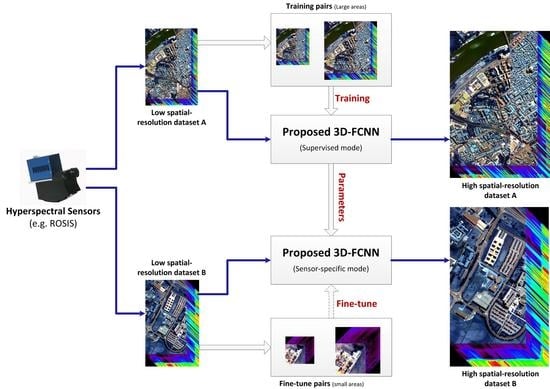
In this paper, 3D convolution is used to explore both spatial context and spectral correlation for spatial SR of HSIs. Consequently, a 3D full convolutional network (3D-FCNN) is proposed for single-image spatial SR of HSIs without any auxiliary information. In order to solve the problem of training deep NN in HSIs where it is very difficult to acquire a large amount of training samples, our proposed 3D-FCNN is extended to a sensor-specific manner such that it can be trained with hyperspectral datasets collected by the same sensor as the targeted dataset. As a result, the requirement of a large amount of training samples from the target scene is avoided. As shown in
Figure 1, our work can be divided into the following steps: (1)
Training: constructing, training and validating 3D-FCNN for SR of HSIs; (2)
Testing: applying the trained network to a sensor-specific task. Specifically, the SR of an HSI can be fulfilled by using a 3D-FCNN trained by HSIs acquired with the same sensor without extra training. Moreover, when possible, such sensor-specific 3D-FCNN can be fine-tuned with only a few training data from the target HSIs to further improve the performance of SR.
2.1. Proposed 3D-FCNN for Spatial SR of HSIs
2.1.1. 2D Convolution
In a traditional 2D CNN, 2D convolution is performed to extract features from the previous layer. As shown in
Figure 2, a convolution kernel is used to filter a small area of the image, so as to generate the feature value of these small regions. For each pixel of the image, the product of its neighboring pixels and the corresponding elements of the filter matrix is calculated and then added as the feature value of this pixel, which can be expressed as
where
is the output feature value targeted at position
,
is the input unit at position
with an offset of
to
,
is the weight for the input
which is located at
in the 2D convolution kernel,
is the bias in the convolution neuron, and
is the activation function. If the kernel has the size
and the input image has the size
, the output feature map will have a smaller size
, in which
.
In general, a convolution layer consists of a set of learnable filters (or kernels) that have small receptive fields, which are trained to learn specific types of features at the same spatial position in the input. In addition, parameters of kernel windows are forced to be identical to all possible locations of the previous layer, which is called weight sharing. Both the weight sharing technology and small receptive fields strategy can effectively reduce the number of parameters and increase the generalization capability of the network. Weights are replicated over the input image, leading to intrinsic insensitivity to translation in the input. A convolutional layer usually contains multiple feature maps so that multiple features can be detected. The network is trained with the back propagation (BP) gradient-descent procedure.
2.1.2. 3D Convolution
Though CNN has achieved great success in 2D convolution, the 2D convolution is only applied in the 2D space to capture spatial features. In 3D hyperspectral applications, the most straightforward method is to perform 2D CNN processing on each band of HSIs. However, such a 2D convolution on multiple images separately does not explore spectral information encoded in contiguous bands, easily resulting in spectral distortion. To this end, the spectral dimension should also be considered in the convolutional kernel to extract spectral features. Therefore, in this paper, 3D convolution instead of 2D convolution is used to simultaneously conduct convolution in both spatial and spectral dimensions to capture spatial-spectral features. As shown in
Figure 3a, 3D convolution is realized by convolving a 3D kernel with the cube formed by stacking multiple contiguous spectral information together. By extending 2D convolution in Equation (1), 3D convolution is calculated as the weighted sum of pixels in a 3D data cube as
where
is the output feature at position
,
represents the input at the position
in which
denotes its offset to
, and
is the weight for input
a(x+i)(y+j)(z+k) with an offset of
in the 3D convolutional kernel. Similar to 2D convolution, the feature cube has a smaller size.
Similar to the 2D convolution, weight sharing technique—in which the kernel weights are replicated across the entire cube—is also used in the 3D convolution such that one kernel extracts one type of feature all over the image cube. In order to explore different kinds of spatial-spectral local feature patterns, as shown in
Figure 3b, multiple 3D convolutions with distinct kernels are applied to the same location in the previous layer.
2.1.3. The Architecture of the Proposed 3D-FCNN
In this paper, as shown in
Figure 4, a 3D-FCNN is constructed for SR of HSIs by using 3D convolution to fully explore spatial-spectral features in the 3D hyperspectral data cube. Considering a single-source low-resolution HSI
, it is firstly up-scaled to
with the same size of desired output
using bicubic interpolation. Since only spatial information is taken into account in bicubic interpolation, 3D convolution is used to further improve the initial SR result
by alleviating spectral distortion. Therefore, the initial SR result
is entered into our 3D-FCNN to generate a high-spatial-resolution HSI
approaching the desired output
as accurately as possible, which can fully take advantages of both spatial context and spectral correlation.
The structure of our proposed 3D-FCNN is shown in
Figure 4. It contains five layers including one input layer, and four convolutional layers where the output of the last convolutional layer is the output of the whole network. Generally, the number of parameters to be optimized is proportional to that of neurons in a CNN. In SR problems, the scale of the input, namely the initial super-resolution result
, heavily influences the scale of the network. In this paper, a sub-image, rather than the entire hyperspectral image, is fed to the 3D-FCNN. Specifically, as shown in
Table 1, the input is restricted as a
-pixel sub-image cube, where
is spatial dimensions,
is the special dimension depending on the sensor properties, and the color channel is set as 1 for HSIs. Therefore, all the filers in the successive convolution layers are designed to learn spectral information from
contiguous spectral bands. It should be noted that larger sub-images can also be used as input to design the 3D-DCNN and its construction is similar to that in this paper. We restrict the network to a relatively small scale to be easily and quickly trained.
As shown in
Figure 4, four 3D convolutional layers are sequentially connected to the input layer to improve the performance of initial SR result by exploring both spatial context and spectral correlation. For the first three convolutional layers, the ‘ReLU’ function is adopted as activation function for nonlinear mapping since it improves models fitting without extra computational cost and over-fitting risk. Suppose the input of neurons in activation layers is represented as
, their output is calculated in an element-wise manner as follows
For the fourth convolutional layer, its output without the effect of activation function is used as the output of the whole network. The size of kernels in convolution layers is of crucial importance in CNN since it greatly affects the performance of the network. The size of different convolutional layers and ‘ReLU’ layers in our proposed 3D-FCNN are listed in
Table 1.
According to
Figure 4 and
Table 1, in the proposed 3D-FCNN, 64 different 3D kernels with size
(
in spatial dimension and 7 in the spectral dimension) are conducted on the input data to generate 64 feature maps of the size
for Layer ‘Conv1’. Layer ‘Conv2’ consists of 32 features maps of the size
, which are obtained by applying 32 different 3D kernels size of
on the input of Conv1. The third convolution layer ‘Conv3’ is obtained by applying nine different 3D kernels of size
, resulting in nine feature maps with a size of
. Finally, the output layer ‘Conv4’ applies a 3D kernel of the size
to produce the output image
with size
. In order to prevent the border effects that occur during training, all convolutions are not padding. Thus, as mentioned earlier, the actual output of the network is smaller than the input. Specifically, according to
Table 1, the proposed 3D-FCNN uses an initial SR result of
to generate an image of
.
Training an end-to-end network requires a cost function to optimize the parameters in the network. In practice, we use the mean squared error (MSE) between outputs and ground-truth as cost function. Considering the actual output of the network is a smaller image, MSE loss function is evaluated only by the difference between the central pixels of ground-truth high-resolution image
and the network output
, which can be calculated as
where
m is the number of training samples,
h and
w represent the length and width of the output of the network
, respectively, and
c is the band of the training samples. Generally, high Peak Signal to Noise Ratio (PSNR) can also be guaranteed by using MSE, which is widely used to evaluate image quality. Let
n represent the number of bits per pixel. The PSNR can be calculated as
The loss function defined by Equation (4) is minimized using adaptive moment estimation (ADAM) with the standard BP algorithm, because it requires less memory, can calculate different adaptive learning rates for different parameters, and is suitable for large datasets and high dimensional space. The main advantage of ADAM is that the learning rate of each iteration has a definite range after the correction of bias, which makes the parameters more stable. In particular, the weight matrices are updated as
where
represents time-step,
represents the gradients at time-step
,
is the biased first moment estimate,
is the biased second moment estimate,
is the bias-corrected first moment estimate,
is the bias-corrected second moment estimate,
is the learning rate,
is the parameter vector, and
are exponential decay rates for the moment estimates.
2.2. Sensor-Specific Implementation
Our proposed 3D-FCNN can be extended to the spatial SR problem of hyperspectral sensors, such as ROSIS and HYDICE. Once the 3D-FCNN is well trained, its parameters can be used for a sensor-specific mission, which means that our trained network can be directly applied to different datasets obtained from the same sensor.
As shown in
Figure 1, when the proposed 3D-FCNN is used for the sensor-specific mission, there are two modes as follows:
- (1)
Unsupervised sensor-specific mode: the parameters involved in the network do not vary when being directly transferred to the target data obtained from the same sensor as the data trained on the proposed 3D-FCNN. As a result, any training data of the target dataset is not required. Thus, this network can be viewed as an unsupervised sensor-specific spatial SR system, which can be directly used for reconstructing high spatial-resolution HSI from the target low spatial-resolution HSI without changing the parameters of networks. In this mode, a large amount of training data and training time is avoided when it is used for the SR of the target scene. It should also be noted that such unsupervised sensor-specific mode is especially effective for the target scene which is acquired with similar imaging condition with the dataset on which the 3D-FCNN is trained.
- (2)
Fine-tuning based sensor-specific mode: the parameters in the network trained under unsupervised sensor-specific mode can be further fine-tuned using the samples from the target dataset obtained by the same sensor. Through such fine-tuning, the performance of unsupervised sensor-specific spatial SR can be further improved. Such fine-tuning based sensor-specific mode is especially effective when the target scene is acquired with different imaging condition with the dataset on which the 3D-FCNN is trained. Only a small number of training samples is required, so the training based on sensor-specific initialization is very fast, compared with previous supervised training with random initialization.
3. Results
In this section, extensive experiments are conducted to verify the performance of the proposed 3D-FCNN for spatial SR of HSIs.
3.1. Datasets
Datasets from two well-known hyperspectral sensors, namely ROSIS and HYDICE, are used for evaluation. For the ROSIS sensor, two scenes that are acquired during a flight campaign over Pavia, northern Italy, i.e., Pavia Centre and Pavia University are selected. The Pavia Centre scene contains 1096 × 1096 pixels, while the Pavia University scene contains 610 × 340 pixels. In the Pavia Centre scene, samples that contain no information are discarded in this experiment and only 1096 × 715 valid pixels are used. The numbers of spectral bands are 102 for Pavia Centre and similarly 103 for Pavia University. For the HYDICE sensor, two datasets are adopted, namely the Washington DC Mall datasets and the Urban dataset. The Washington DC Mall datasets image contains 1280 × 307 pixels over 191 bands of the original 224 atmospherically corrected bands which are adopted by removing the channels associated with H2O and OH absorption bands. The Urban HYDICE datasets is of size 307 × 307 and contains 210 atmospherically corrected bands.
These four datasets are used as ground-truth of high spatial-resolution HSIs to train and evaluate the performance of the proposed 3D-FCNN based framework for spatial SR. In order to simulate low spatial-resolution HSIs, these two images are firstly down-sampled using Gauss kernels. The size of sub-images used for training is set as , which is obtained by overlapping from the original dataset. The proposed 3D-FCNN based framework is designed, trained, and tested based on the Keras framework using the TensorFlow backend. The BP strategy is adopted to train the network. For the ADAM based training, the base learning rate is 0.00005.
3.2. Performance Evaluation
Many assessment methods have been used to evaluate the quality of a reconstructed hyperspectral image for SR and restoration [
59]. In this experiment, the performance of SR for HSIs is evaluated by comparing the reconstructed high spatial-resolution HSI with the ground-truth data from two aspects: the spatial reconstruction quality of each band image at image levels and the spectral reconstruction quality of each spectrum at pixel-levels.
To evaluate the spatial reconstruction quality, the mean peak signal-to-noise ratio (MPSNR) and the mean structural similarity (MSSIM) index are adopted. The MPSNR is defined as
where
MAXi is the maximal pixel value in the
i-th band image, and
is the
of the
i-th band image. The MSSIM between reconstructed image
and its ground truth
is defined as
where
and
represents the
i-th band image of
and
, respectively,
and
are the mean of
and
, respectively,
and
are the variance of
and
, respectively,
is the covariance of
and
, and
and
are constants that are set as 0.0001 and 0.0009, respectively.
In order to evaluate the spectral reconstruction quality, the spectral angle mapper (SAM) between the reconstructed spectra and their corresponding ground-truth spectra is used. The SAM between two spectra
and
is defined as
where
represents the dot product of
and
, and
represents 2-norm of vectors.
Generally, a higher MPSNR and MSSIM value means a better visual quality, and a lower SAM value implies less spectral distortion and a higher quality of spectral reconstruction.
3.3. Experimental Results on Hyperspectral Datasets Acquired by ROSIS Sensor
Two datasets acquired by ROSIS sensor, namely Pavia Centre dataset and Pavia University dataset, were used to evaluate the performance of the proposed 3D-FCNN for SR. These two datasets are complemented to 103 bands by setting the missing bands as 0.
3.3.1. Experimental Results of Spatial SR with the Proposed 3D-FCNN Method
The performance of the proposed 3D-FCNN for spatial SR is evaluated over the two selected datasets. For each dataset, a sub-region is selected to validate the performance of our proposed 3D-FCNN, while the remaining pixels are used for training. In order to simulate low spatial-resolution HSIs, these two images are firstly down-sampled by a factor of 2. In addition, different levels of additive Gaussian white noise, measured by signal-to-noise ratio (SNR), are added to the low spatial-resolution images to verify the robustness of the proposed 3D-FCNN to noises.
Five strategies are chosen as the baseline for comparison: Bicubic SR, Bilinear SR, SR by nearest neighbor, SRCNN [
40,
42] in a band-by-band manner (namely misSRCNN in [
44]) and three-band-wise manner (denoted as 3B-SRCNN). The qualitative comparison results of all the considered algorithms are listed in
Table 2. Their corresponding visual results are shown in
Figure 5 and
Figure 6, respectively. It is also observed that: (1) the proposed 3D-FCNN obviously outperforms all the other algorithms all over these two datasets by ROSIS sensor with the highest MPSNR and MSSIM values and lowest SAM for all the cases; (2) The proposed 3D-FCNN provides better results no matter how noisy the dataset is. The average improvements in MPSNR are 2.572 dB and 2.878 dB, and in MSSIM are 0.033 and 0.032 compared with Bicubic when
dB and
dB, respectively, indicating that the proposed 3D-FCNN is robust to noises in low spatial-resolution HSI; (3) The proposed 3D-FCNN based algorithm provides much better spectral fidelity (i.e., lower SAM) compared with SRCNN (msiSRCNN and 3B-SRCNN).
Figure 7 further lists the spectra of several typical ground materials after spatial SR. It can be observed that the spectra reconstructed by the proposed 3D-FCNN is closer to their ground-truth than that by the bicubic spatial interpolation, demonstrating that the proposed 3D-FCNN can better maintain spectral characteristics during spatial SR. This is because both spatial context in neighboring areas and spectral correlation in full-band images are considered in the proposed method by 3D convolution; (4) The proposed 3D-FCNN based algorithm also achieves best spatial reconstruction for all the cases, which has the highest MPSNR and MSSIM values. Compared with the Bicubic algorithm, the average improvements are 2.849 dB in terms of MPSNR and 0.035 for MSSIM.
3.3.2. Experimental Results of SR for Different Up-Sampling Factors
In this subsection, the SR results of different up-sampling factors are discussed. The low spatial-resolution HSIs are simulated by down-sampling the high spatial-resolution HSI with the factor 2, 3 and 4, respectively. Then different SR algorithms are used for spatial SR. Similar to previous experiments, only a
sub-region from the Pavia Centre datasets is used for validation of the performance of our proposed 3D-FCNN, while all the remaining areas are used for training.
Table 3 lists the quantitative results by different SR algorithms for different up-sampling factors over the Pavia Centre area. It is observed that, the performance of our proposed 3D-FCNN outperforms all the other algorithms with different up-sampling factors. When the up-sampling factor increases, the superiority of our proposed 3D-FCNN becomes less obvious. This is because the problem of SR with a higher up-sampling factor is more difficult. However, even for 4 times spatial SR, the proposed 3D-FCNN achieves an improvement of 1.74 in MPSNR, 0.045 in MSSIM, and 0.287 in SAM, respectively, compared with the Bicubic method.
3.3.3. Experimental Results of Sensor-Specific SR by the Proposed 3D-FCNN
In this experiment, the 3D-FCNN is used for spatial SR of HSIs in a sensor-specific manner, which means that it is trained on one dataset and directly applied for spatial SR of other datasets acquired by the same sensor without any tuning of parameters. Specifically, the 3D-FCNN trained on the Pavia Centre dataset is used for spatial SR of the Pavia University dataset, and the model trained on the Pavia University dataset is used for spatial SR of the Pavia Centre dataset. Such sensor-specific manner can be viewed as an unsupervised version of our proposed 3D-FCNN for spatial SR of HSIs since training samples from the target scene are not required. In addition, the performance of fine-tuning for sensor-specific SR, in which the parameters of sensor-specific 3D-FCNN is fine-tuned with a limited number of available training samples from target datasets, is also tested.
Table 4 lists the quantitative results from our proposed 3D-FCNN for spatial SR of the two datasets from the ROSIS sensor. The results of previous supervised 3D-FCNN are also listed as benchmark results. It is observed that, the performance of spatial SR by the proposed 3D-FCNN does not degrade even if it is not trained by the targeted datasets, demonstrating the effectiveness of the proposed sensor-specific strategy for spatial SR of hyperspectral sensors. The visual results of our proposed 3D-FCNN for spatial SR of the Pavia Centre dataset and the Pavia University dataset are shown in
Figure 8 and
Figure 9, respectively, including both supervised mode that is trained by samples from the target scene and sensor-specific mode that is trained by other datasets from the same sensor. These results also confirmed that our proposed sensor-specific mode is very effective for spatial SR of HSIs. However, it avoids the requirement of a huge amount of training samples from the target scene and the time-consuming training.
It is also observed from
Table 4 that the fine-tuning process of training sensor-specific 3D-FCNN with a few samples from the target dataset cannot improve the performance of sensor-specific very much. This may be because these two datasets are acquired during one flight and the imaging condition, e.g., acquisition time, weather, atmosphere, texture of images, etc., does not vary much. Therefore, we further evaluated the performance of our proposed 3D-FCNN on two datasets acquired at different imaging conditions by the HYDICE sensor.
3.4. Experiments on Hyperspectral Datasets Acquired by the HYDICE Sensor
Two datasets acquired by the HYDICE sensor, namely the Washington DC Mall and Urban datasets, are used to evaluate the performance of the proposed 3D-FCNN. As with the ROSISI sensor, the two datasets are complemented to 210 bands by setting the missing bands as 0.
3.4.1. Experimental Results of SR with the Proposed 3D-FCNN Method
Since the Urban dataset is too small to train the proposed 3D-FCNN, only the Washington DC Mall dataset is selected to evaluate the performance of the proposed 3D-FCNN for SR in supervised mode. Unlike the ROSIS sensor, we selected a larger region with 600 × 307 pixels to test the performance of our proposed 3D-FCNN, while the remaining pixels are used for training. The image is firstly down-sampled by a factor of 2 and additive Gaussian white noises are added to the simulated low-dimensional HSI such that the robustness of the 3D-FCNN is tested for images with different SNRs. Five strategies are chosen as the baseline for comparison: Bicubic SR, Bilinear SR, SR by nearest neighbor, SRCNN [
40,
42] in a band-by-band manner (namely misSRCNN in [
44]) and three-band-wise manner (denoted as 3B-SRCNN).
The qualitative comparison results of all the considered algorithms are listed in
Table 5. These results also confirm similar conclusions from previous experiments: (1) the performance of our 3D-FCNN obviously outperforms traditional methods, i.e., Bicubic SR, Bilinear SR and SR by nearest neighbor; (2) the spectral distortion caused by applying SRCNN of natural images directly to HSIs in band-wise manner or 3-band-group manner can be greatly alleviated by the 3D convolution in the proposed 3D-FCNN algorithm; (3) the proposed 3D-FCNN is robust to noise. Even in very noisy cases when
dB, our proposed 3D-FCNN improves the performance of 3B-FCNN (the second best results) by about 2.5 dB in MPSNR, 0.02 in MSSIM, and 0.2 in SAM. The visual results of all these algorithms are also listed in
Figure 10, which demonstrate the superiority of the proposed 3D-FCNN for spatial SR of HSIs.
3.4.2. Experimental Results of Sensor Specific SR for the HYDICE Sensor
In this experiment, the 3D-FCNN trained on the Washington DC Mall dataset is directly applied for spatial SR of the Urban dataset in a sensor-specific manner. The performance of fine-tuning is also tested. The spatial SR results of the Urban dataset using sensor-specific 3D-FCNN are listed in
Table 6. It is observed that the performance of sensor-specific 3D-FCNN can be effectively improved by the fine-tuning process, especially for the quality of spectral reconstruction. When more training samples from the target scene are used for fine-tuning, slightly better results can be achieved. This is because these two datasets are acquired under different conditions, i.e., different time, weather, atmosphere, etc. As shown in these results, the performance of sensor-specific spatial SR can be further improved when even a small amount of training samples from the target scene is used for fine-tuning. These conclusions are also confirmed by the visual results listed in
Figure 11.
4. Discussion
The 3D-FCNN is proposed to learn an end-to-end full-band mapping between low and high spatial-resolution HSIs. It can effectively reconstruct high spatial-resolution HSI using a single low spatial-resolution HSI without any auxiliary information. According to previous experiments, its sensor-specific version can restore a high spatial-resolution HSI without the requirement of training on it. Generally, fine-tuning by using training samples from the target scene can improve the performance of SR. However, if the target scene is acquired with similar conditions to the scene that the 3D-FCNN is trained over, there is no need to fine-tune the network for SR since the performance of SR cannot be further improved.
Table 7 lists the computation time of three CNN based spatial SR algorithms for the Pavia Centre dataset by the ROSIS sensor. All these algorithms are implemented on a computer with one GPU card (NVIDI GTX1070 with 16GB memory). It is observed that, in order to learn the spectral correlation in adjacent band images, our proposed 3D-FCNN takes more time for training. However, once our network is well trained, it takes less than one second to reconstruct an image, indicating that it is computationally effective when working under an unsupervised sensor-specific manner.
In order to further evaluate the performance of our proposed 3D-FCNN with different parameters for SR, various experiments are conducted over the Pavia University dataset by varying different parameters involved in the proposed 3D-FCNN, including the number of convolutional layers, the size of input, activation function, filter size, and the size of receptive field. The corresponding results are listed in
Table 8,
Table 9,
Table 10,
Table 11 and
Table 12.
As shown in
Table 8, the 3D-FCNN with four convolutional layers slightly outperforms that with other numbers of convolutional layers. Actually, the 3D-FCNN with different convolutional layers does not vary much. Here, four convolutional layers are adopted since more convolutional layers will bring about many more parameters to be learned and the computational time for training and testing will increase rapidly.
In
Table 9, the 3D-FCNN with the input of 33x33xc slightly outperforms that with other inputs. Moreover, larger inputs also result in more parameters to be trained.
The 3D-FCNN with the activation function of ‘Relu’ slightly outperforms the other two well-known activation functions, namely ‘Tanh’ and ‘PRelu’, as tabulated in
Table 10.
In terms of the filter size, as shown in
Table 11, the 3D-FCNN with ‘64-32-9-1’ slightly outperforms that with other filters, where the numbers in these filters represent the last dimension of filters listed in ‘
Table 1’ (in the manuscript) for the four convolutional layers, respectively.
As for the size of receptive field in
Table 12, the 3D-FCNN with a receptive field of 16 produces the best results. However, the number of parameters are much more than that with a smaller receptive field. Therefore, 12 is adopted to achieve the balance between the performance of SR and computational complexity.